U odjeljku 2.2.6. uveli smo treću ravninu projekcije ili ravninu bokocrta koja je okomita na ravnine tlocrta i nacrta, odnosno na ravnine \(\small \Pi_1\) i \(\small \Pi_2\). Međutim, ponekad je bolje izabrati ravninu okomitu samo na jednu od njih. Primjerice, kada želimo prostorne figure dovesti u povoljniji položaj prema ravninama projekcije čime se olakšava rješavanje nekih problema.
Treću ravninu projekcije \(\small \Pi_3\), koja je okomita ili na ravninu \(\small \Pi_1\) ili na ravninu \(\small \Pi_2\), nazivamo ravninom stranocrta.
- Ako je ravnina stranocrta \(\small \Pi_3\)\(^*\) okomita na ravninu \(\small \Pi_1\) tada je ona 1. projicirajuća ravnina te njihovu presječnicu označavamo s \(\small_1 x_3\) (\(\small \Pi_1 \cap \Pi_3 = \) \(\small_1 x_3\))
- Ako je ravnina stranocrta \(\small \Pi_3\) okomita na ravninu \(\small \Pi_2\) tada je ona 2. projicirajuća ravnina te njihovu presječnicu označavamo s \(\small_2 x_3\) (\(\small \Pi_2 \cap \Pi_3 = \) \(\small_2 x_3\))
Stranocrt točke
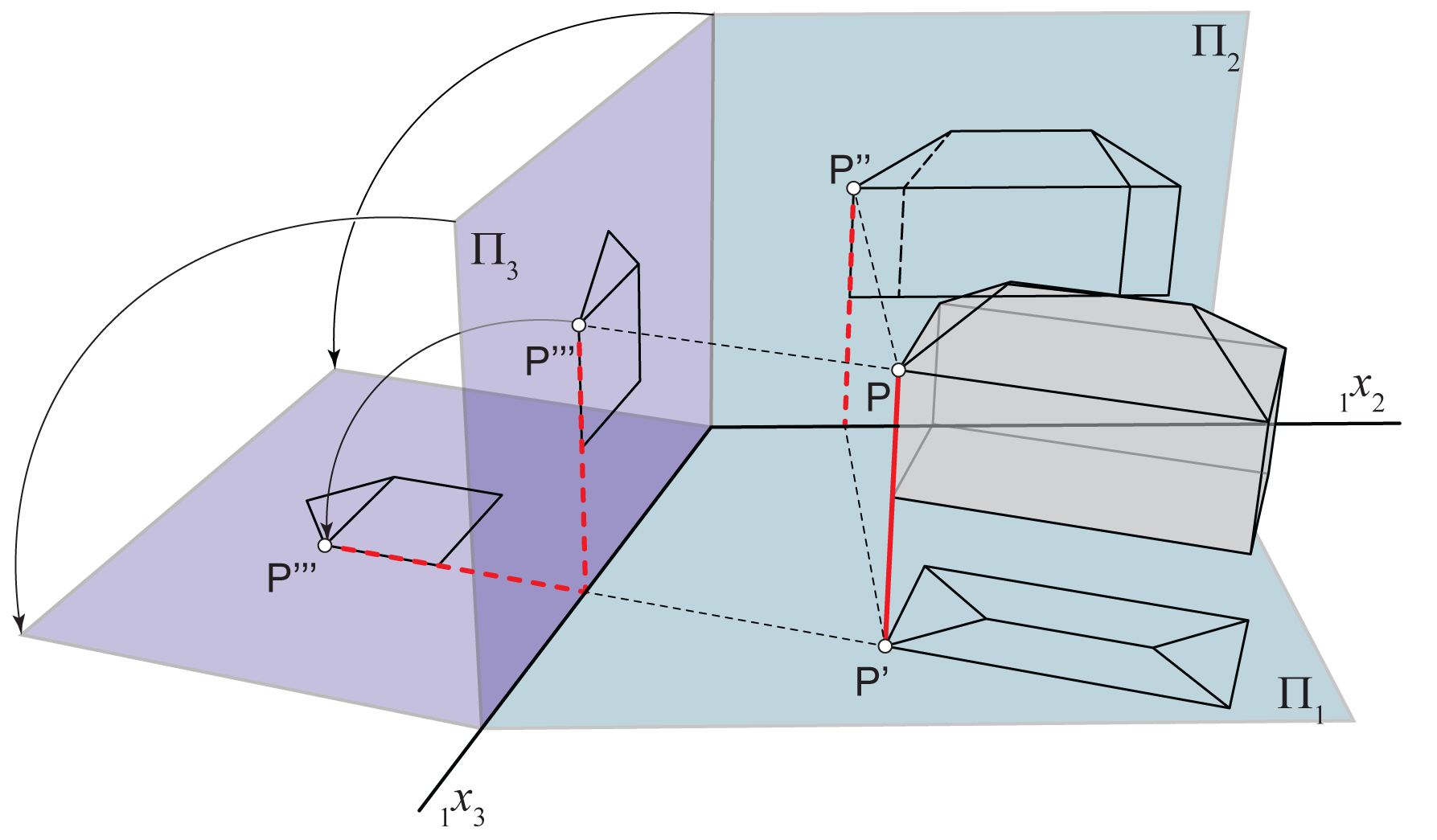
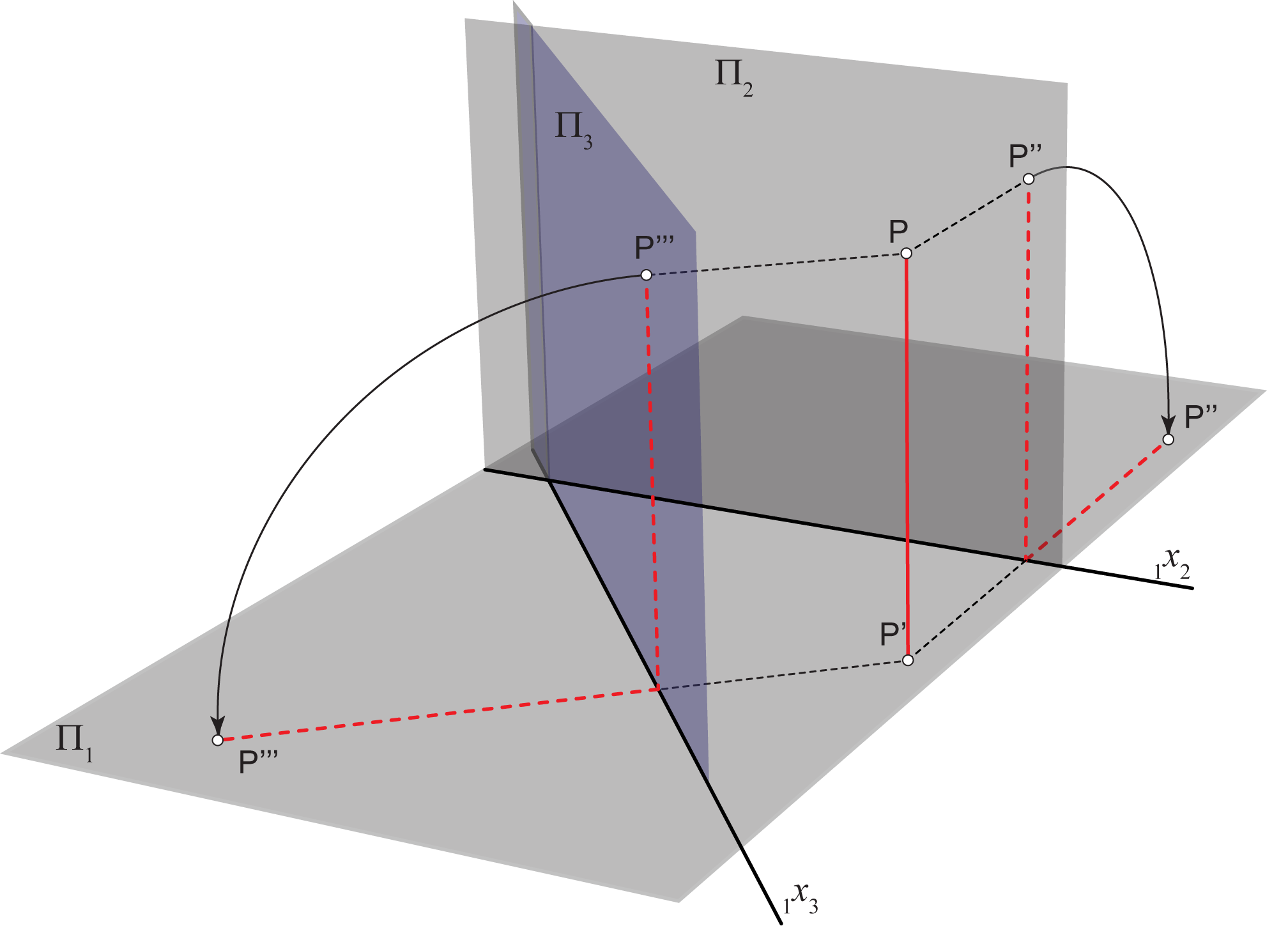
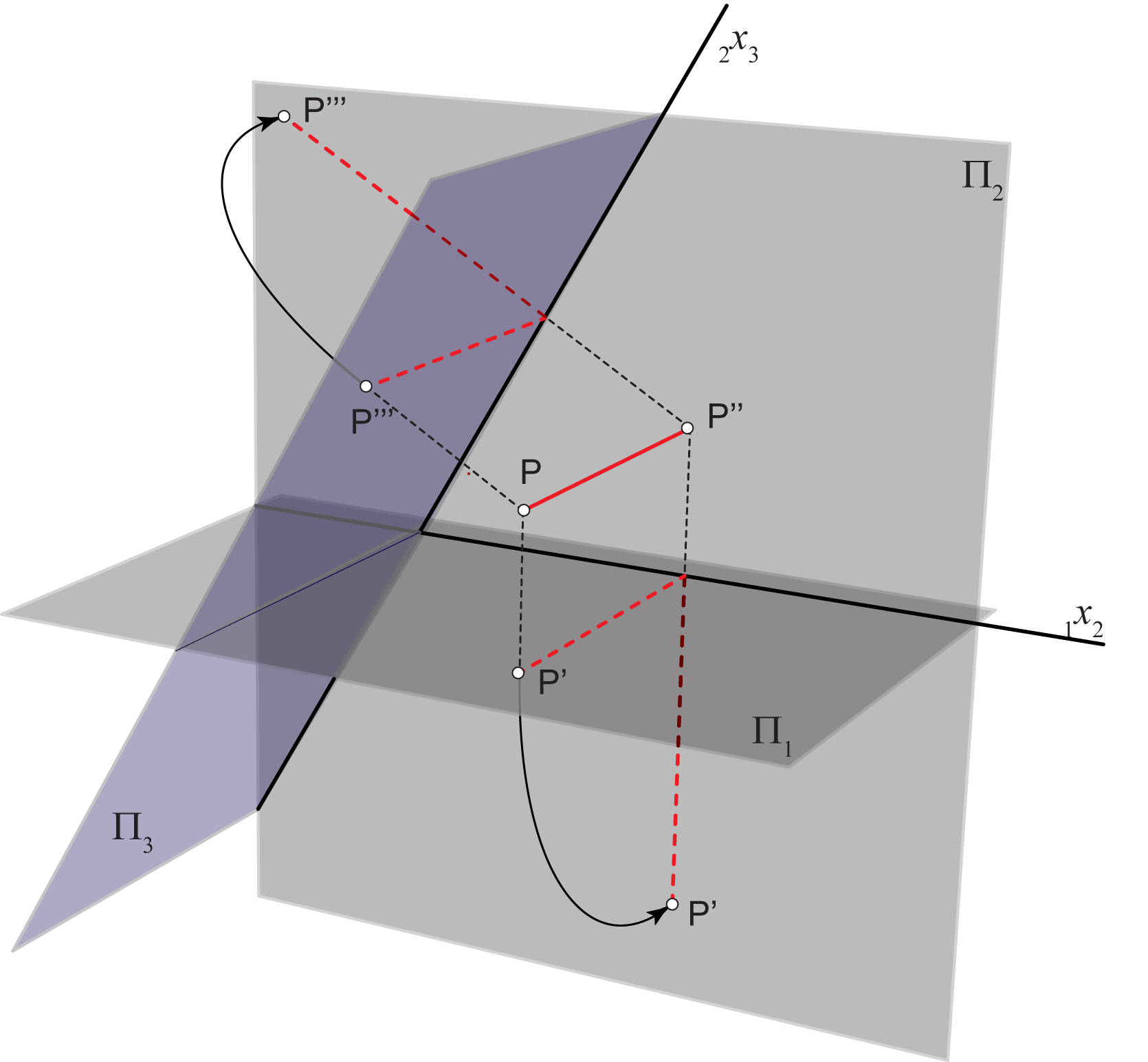
Neka je \(\small P\) bilo koja točka prostora. Ortogonalnu projekciju točke \(\small P\) na ravninu \(\small \Pi_3\) nazivamo trećom projekcijom ili stranocrtom točke \(\small P\) i označavamo \(\small P'''\).
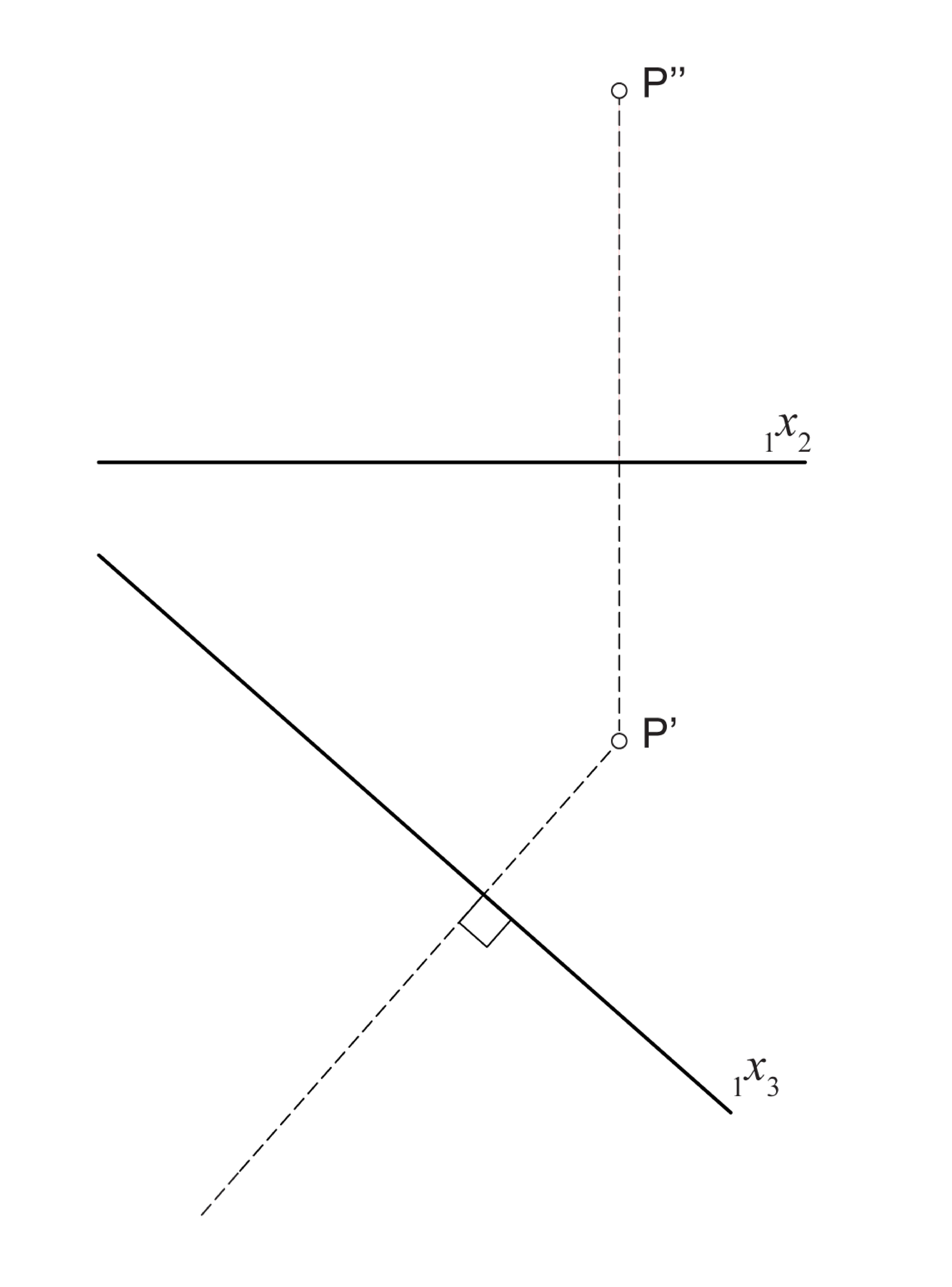
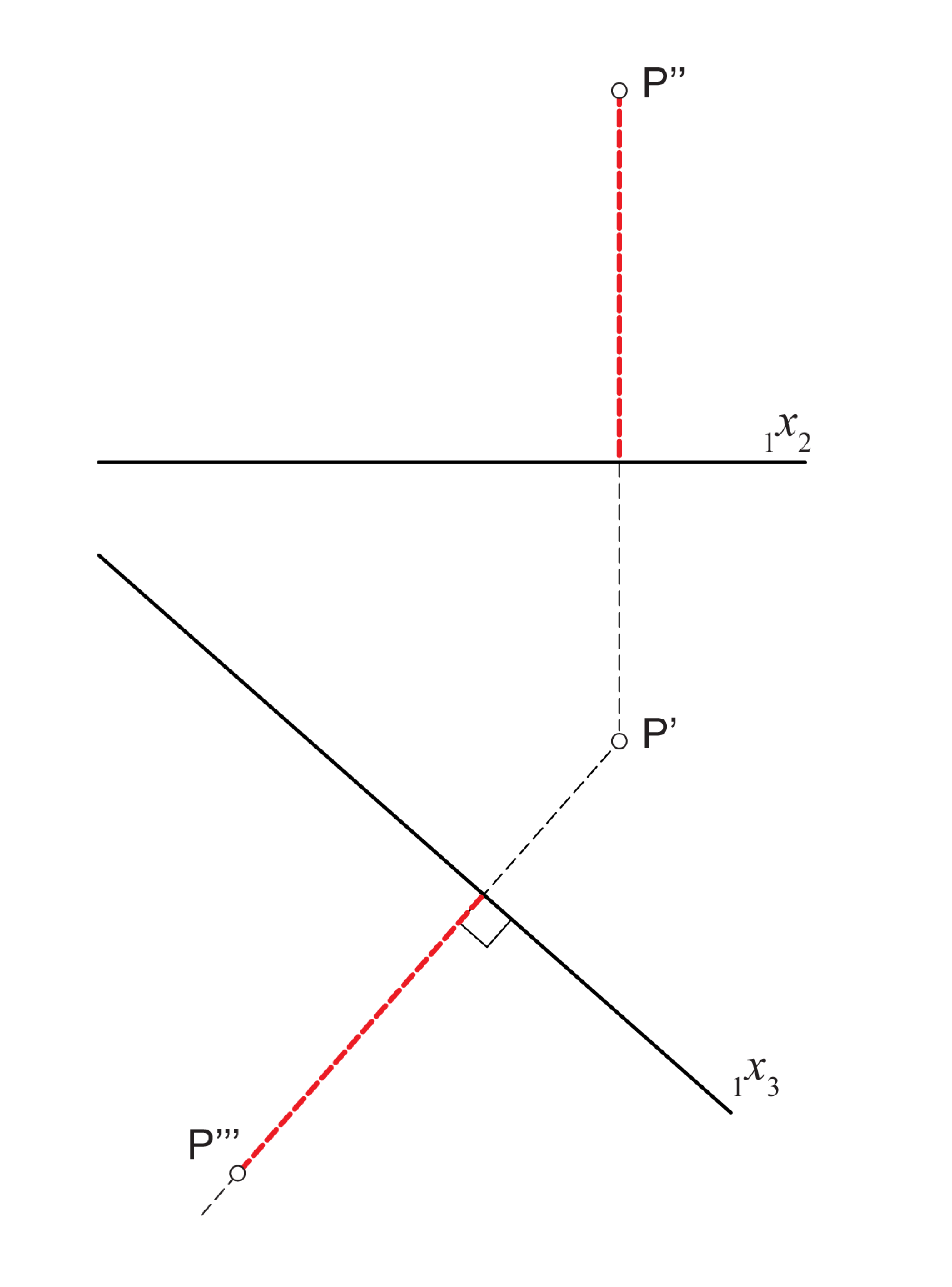
Ako smo izabrali ravninu stranocrta \(\small \Pi_3\) okomito na ravninu \(\small \Pi_1\) tada ravninu stranocrta rotiramo oko osi \(\small_1 x_3\) za \(\small 90^\circ\) u ravninu \(\small \Pi_1\). Ovu rotaciju nazivamo prevaljivanjem, a stranu na koju \(\small \Pi_3\) prevaljujemo u ravninu \(\small \Pi_1\) odabiremo po volji (kako nam odgovara u pojedinom zadatku). Vidi sliku 177.
Kao što točke \(\small P'\) i \(\small P''\) leže na ordinali okomitoj na os \(\small _1x_2\), tako i točke \(\small P'\) i \(\small P'''\) leže na ordinali okomitoj na os \(\small_1 x_3\).
Za stranocrt točke \(\small P\) vrijedi \(\small \,\,d(P''',\,_1 x_3) = d(P'' ,\,_1 x_2) = d(P, \Pi_1\)).
Konstrukcija točke \(\small P'''\) za ovako izabranu ravninu \(\small \Pi_3\) prikazana je na prezentaciji 22.

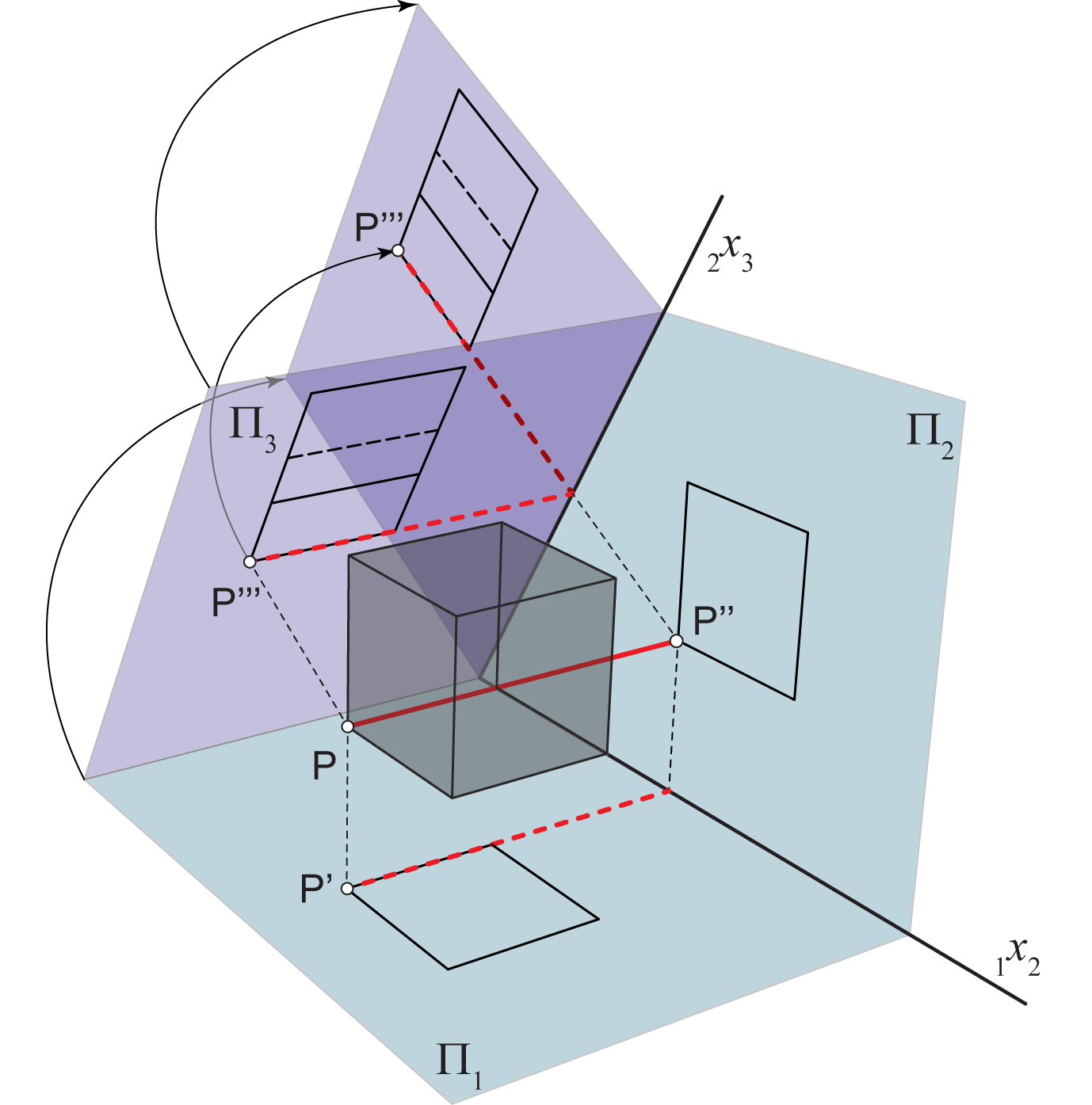
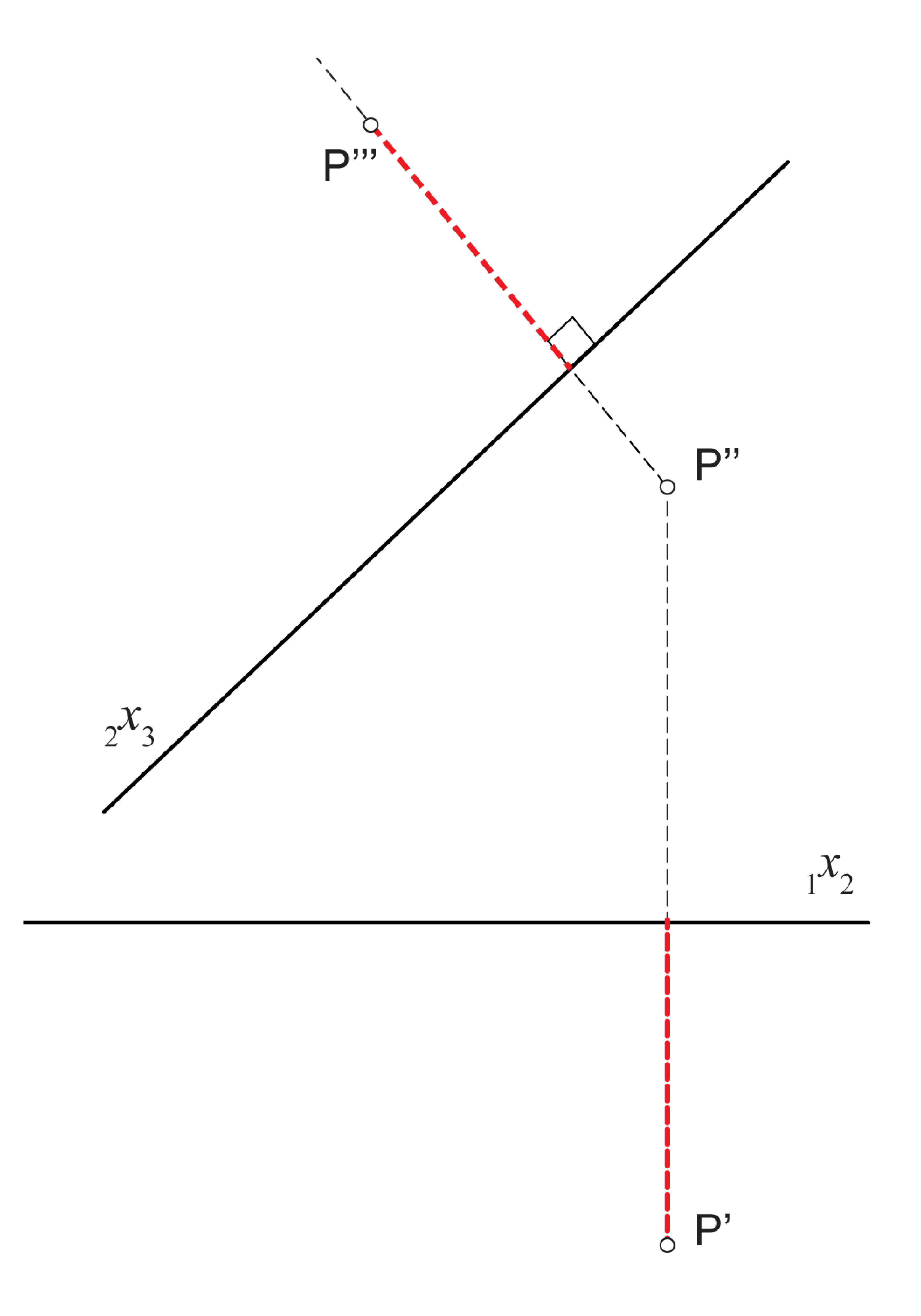
Ako je \(\small \Pi_3\) okomita na ravninu \(\small \Pi_2\), tada ravninu stranocrta rotiramo oko osi \(\small_2 x_3\) za \(\small 90^\circ\) u ravninu \(\small \Pi_2\). Isto kao u gornjem postupku, stranu na koju rotiramo ravninu \(\small \Pi_3\) odabiremo po volji. Sada točke \(\small P''\) i \(\small P'''\) leže na ordinali okomitoj na os \(\small_2 x_3\).
Za ovakav stranocrt točke \(\small P'''\) vrijedi \(\small \,\,d(P''',\,_2 x_3) = d(P' ,\,_1 x_2) = d(P, \Pi_2\)) .
Konstrukcija stranocrta točke \(\small P\) za ovako izabranu ravninu \(\small \Pi_3\) prikazana je na prezentaciji 23.



Stranocrt pravca i dužine
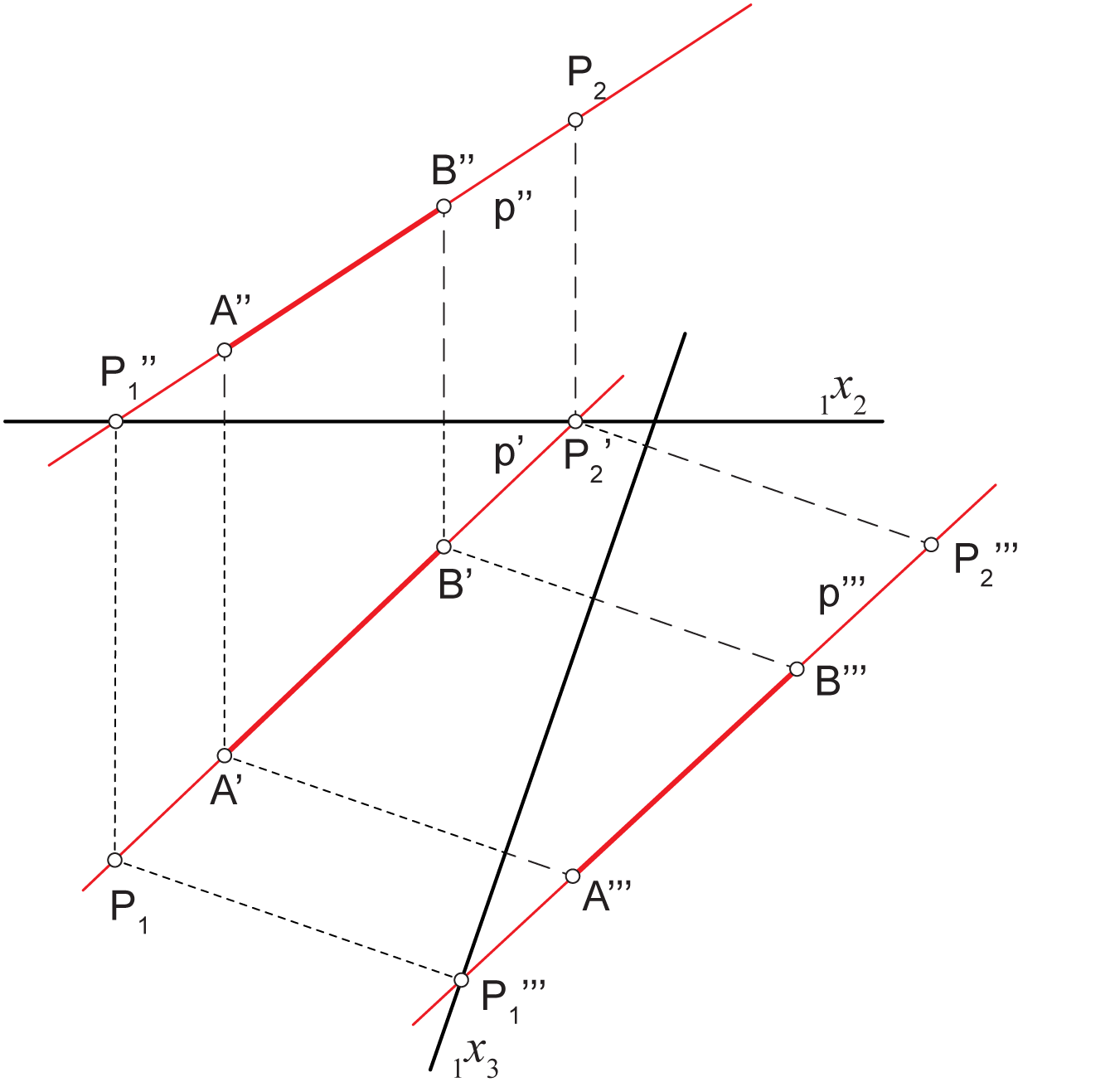
Neka je \(\small p\) bilo koji pravac prostora u općem položaju prema proizvoljno izabranoj ravnini stranocrta \(\small \Pi_3\).
- Stranocrt \(\small p'''\) pravca \(\small p\) možemo konstruirati pomoću bilo koje dvije njegove točke, primjerice pomoću njegovih probodišta \(\small P_1\) i \(\small P_2\), ili pomoću proizvoljno odabrane dvije njegove točke \(\small A\) i \(\small B\).
Na slici 179 prikazana je konstrukcija stranocrta pravca \(\small p\), pri čemu je ravnina stranocrta \(\small \Pi_3\) odabrana tako da je okomita na ravninu \(\small \Pi_1\).
Uočite da je ovime opisano i određivanje stranocrta dužine \(\small\overline{AB}\) s obzirom na to da svaka dužina leži na nekom pravcu.
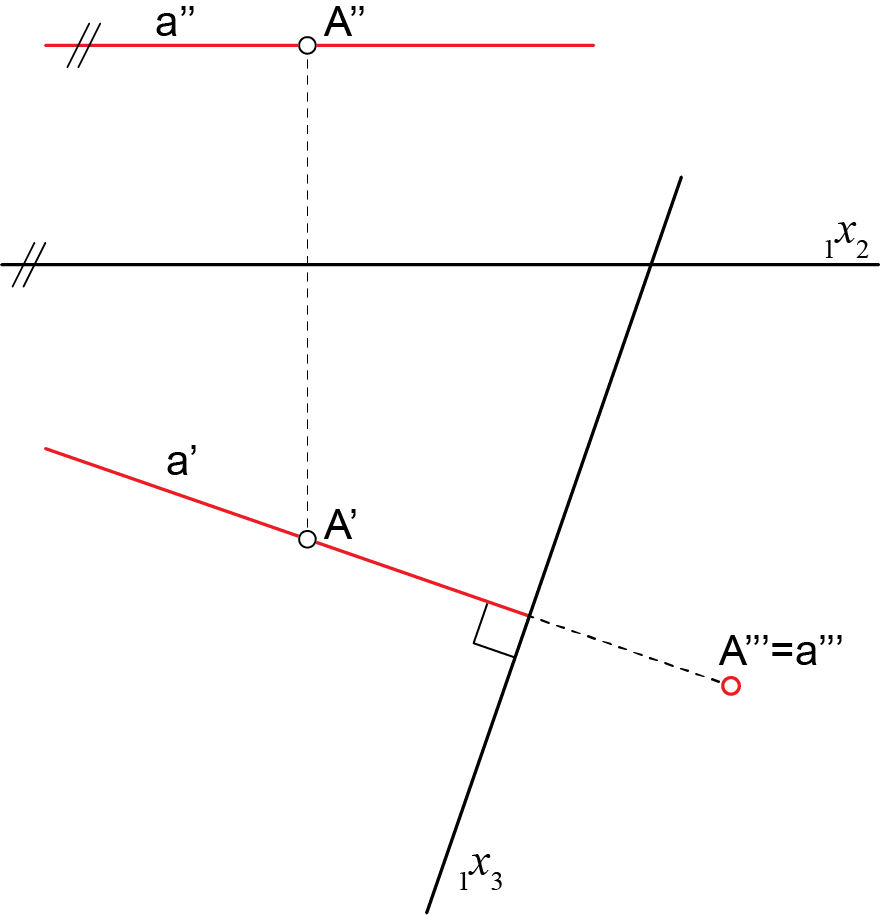
Ako je pravac okomit na ravninu stranocrta, njegov je stranocrt točka (vidi sliku 180).
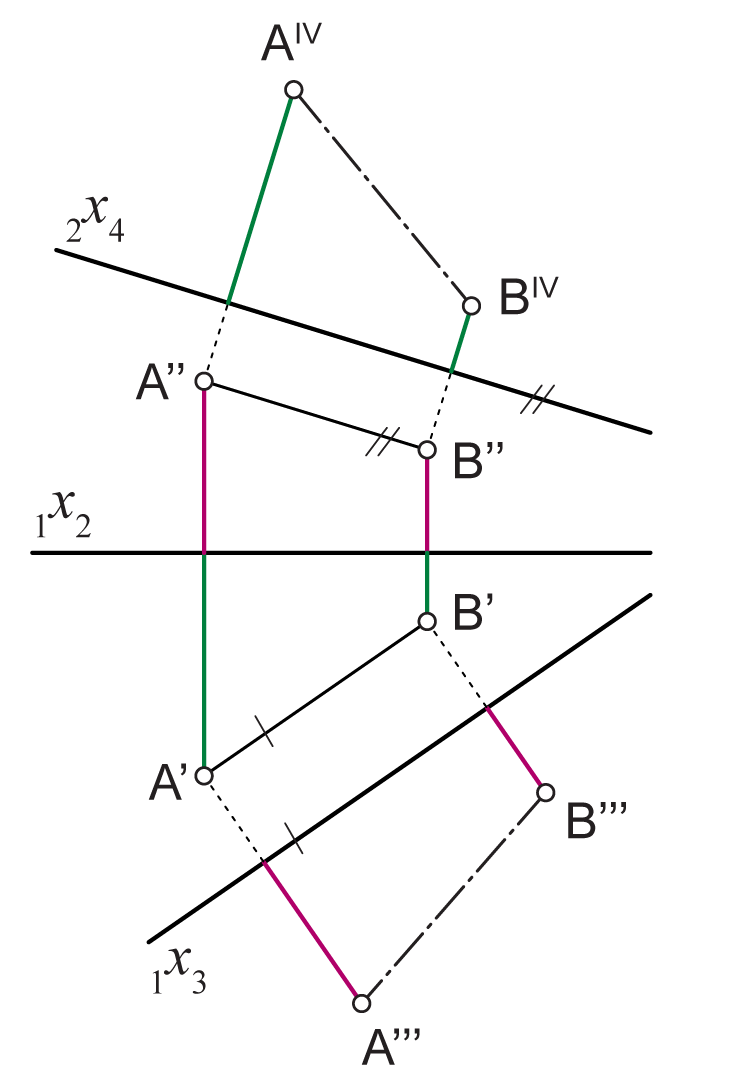
Ako je ravnina stranocrta \(\small \Pi_3\) izabrana tako da je paralelna sa zadanom dužinom \(\small\overline{AB}\), tada je duljina njezinog stranocrta \(\small\overline{A'''B'''}\) jednaka duljini dužine \(\small\overline{AB}\) (vidi sliku 181).
Stranocrt ravnine
Presječnicu \(\small s_3\) ravnine \(\small\Sigma\) i ravnine stranocrta \(\small \Pi_3\) nazivamo stranocrtnim tragom ravnine \(\small\Sigma\).
Ako je ravnina \(\small\Sigma\) u općem položaju prema ravnini stranocrta \(\small \Pi_3\), njezin će stranocrt biti cijela ravnina \(\small \Pi_3\). Međutim, ako je ravnina \(\small\Sigma\) okomita na ravninu stranocrta \(\small \Pi_3\), sve njezine točke projicirat će se u stranocrtu na stranocrtni trag \(\small s_3\).
Pri rješavanju zadataka birat ćemo upravo ovakav položaj ravnine stranocrta, jer se tada zadatak koji sadrži opću ravninu svodi na zadatak s projicirajućom ravninom.
- Ako je stranocrtna ravnina \(\small \Pi_3\) okomita na ravnine \(\small \Pi_1\) i \(\small\Sigma\), okomita je i na njihovu presječnicu - trag \(\small s_1\). Dakle, trag \(\small s_1\) okomit je na sve pravce ravnine \(\small \Pi_3\) pa i na os \(\small_1 x_3=\Pi_1\cap\Pi_3\)
- Ako je stranocrtna ravnina \(\small \Pi_3\) okomita na ravnine \(\small \Pi_2\) i \(\small\Sigma\), tada je stranocrtna os \(\small_2 x_3\) okomita na trag \(\small s_2\)
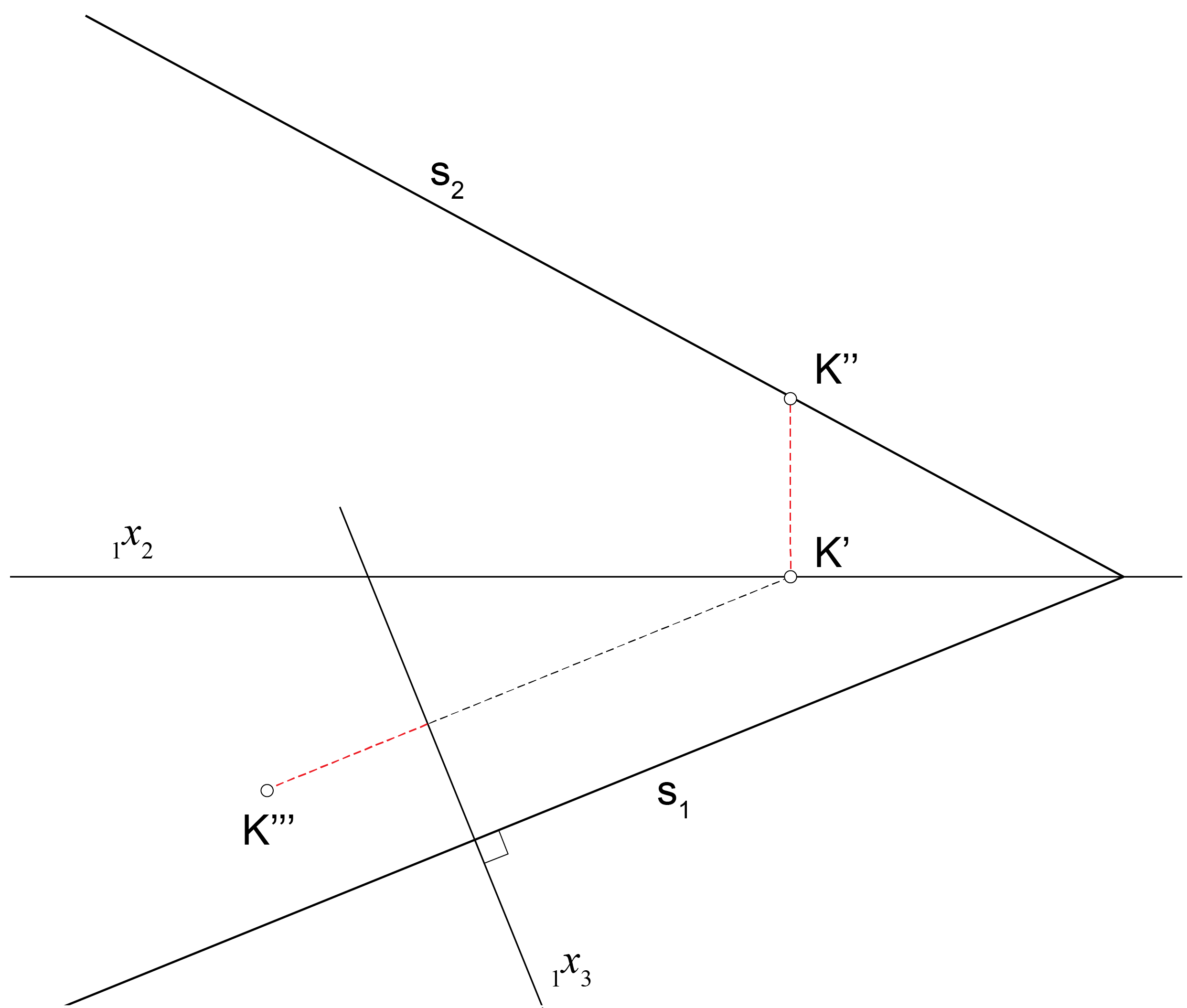
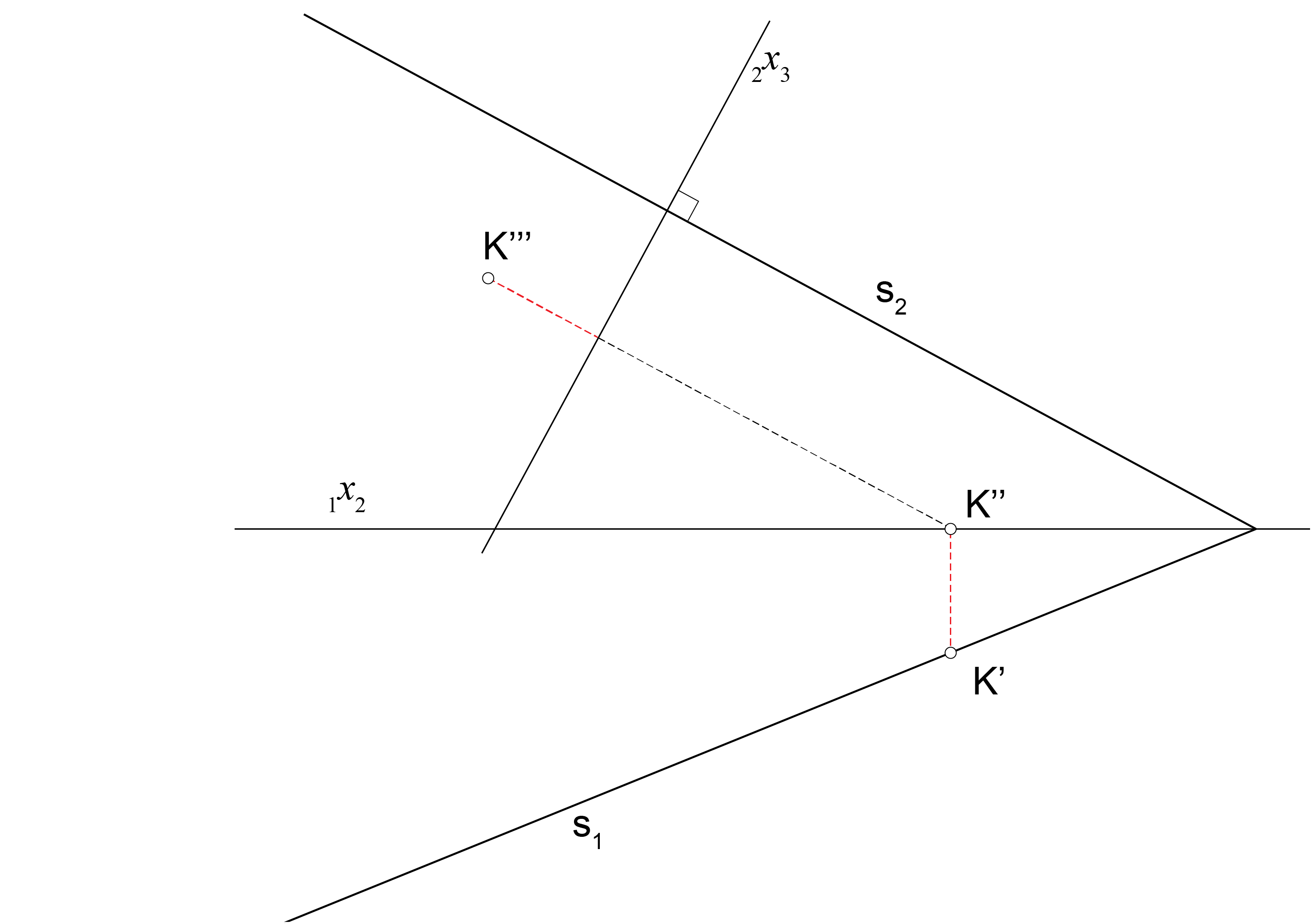
Za konstrukciju trećeg traga \(\small s_3\) ravnine \(\small\Sigma\), koja je 3. projicirajuća, dovoljno je odrediti stranocrt samo jedne točke \(\small K\in \Sigma\).
Pritom točku \(\small K\in \Sigma\) odabiremo tako da određivanje njezinih projekcija bude što jednostavnije. Primjerice, \(\small K\in s_2\) ako je \(\small \Pi_3 \perp\Pi_1\) ili \(\small K\in s_1\) ako je \(\small \Pi_3 \perp\Pi_2\). Vidi prezentacije 24 i 25.






Zadatak 1: Postavite ravninu stranocrta \(\small \Pi_3\) tako da projekcija trokuta \(\small \triangle ABC\) bude dužina (slika 182).

Trokut \(\small \triangle ABC\) će se u stranocrtu projicirati u dužinu ako je ravnina trokuta okomita na stranocrtnu ravninu \(\small \Pi_3\)
Zadatak rješavamo tako da odredimo ravninu trokuta \(\small \triangle ABC\), te okomito na nju i jednu ravninu projekcije (\(\small \Pi_1\) ili \(\small\Pi_2\)) postavimo ravninu stranocrta
RJEŠENJE (Prezentacija 26)
Zadatak 2: Zadana je ravnina \(\small\mathrm P\) svojim tragovima i pravac \(\small p\) svojim projekcijama (slika 183). Odredite probodište \(\small P\) pravca \(\small p\) i ravnine \(\small\mathrm P\).

Stranocrtnu ravninu postavljamo okomito na ravninu \(\small\mathrm P\)
Sjecište stranocrtnog traga ravnine \(\small\mathrm P\) i stranocrta pravca \(\small p\) je stranocrt traženog probodišta \(\small P\), odnosno \(\small P'''=r_3\cap p'''\)
RJEŠENJE (Prezentacija 27)
Zadatak 3: Zadana je ravnina \(\small\mathrm P\) svojim tragovima i točka \(\small P\) svojim projekcijama (slika 184). Odredite udaljenost točke \(\small P\) od ravnine \(\small\mathrm P\).

Udaljenost točke \(\small P\) od ravnine \(\small\mathrm P\) jednaka je udaljenosti točke \(\small P\) do nožista \(\small N\) normale položene točkom \(\small P\) na ravninu \(\small\mathrm P\)
Postavljamo ravninu stranocrta \(\small \Pi_3\) okomito na ravninu \(\small\mathrm P\)
Budući da je dužina \(\small \overline{PN}\) okomita na ravninu \(\small\mathrm P\) ona je paralelna s ravninom stranocrta. Stoga se ta dužina u tom stranocrtu projicira u pravoj veličini
RJEŠENJE (Prezentacija 28)
Zadatak 4: Zadane su paralelne ravnine \(\small\mathrm P\) i \(\small\mathrm E\) svojim tragovima (slika 185). Odredite njihovu udaljenost.

Postavimo ravninu stranocrta \(\small \Pi_3\) okomito na ravnine \(\small\mathrm P\) i \(\small\mathrm E\)
Na temelju prethodnog zadatka zaključujemo da je u tom slučaju udaljenost između ravnina \(\small\mathrm P\) i \(\small\mathrm E\) jednaka udaljenosti stranocrtnih tragova \(\small r_3\) i \(\small e_3\)
RJEŠENJE (Prezentacija 29)
Zadatak 5: Odredite presjek zadane piramide ravninom \(\small\mathrm E\) (Slika 186).

Presjek piramide i ravnine je mnogokut. Vrhovi tog mnogokuta su probodišta bridova piramide s ravninom \(\small\mathrm E\), dok su stranice presječnice pobočki piramide i ravnine \(\small\mathrm E\)
Zadatak rješavamo tako da postavimo ravninu stranocrta \(\small \Pi_3\) okomitu na ravninu \(\small\mathrm E\) jer će se tada presječni mnogokut u stranocrtu projicirati u dužinu koja leži na stranocrtnom tragu \(\small e_3\)
RJEŠENJE (Prezentacija 30)