U općem se slučaju svaki mnogokut ortogonalnom projekcijom projicira u mnogokut s istim brojem stranica i vrhova. Međutim, ako mnogokut leži u projicirajućoj ravnini, jedna će njegova projekcija biti dužina. Uz pomoć postupaka nacrtne geometrije koje ste do sada naučili, za takve ćete slučajeve moći odrediti projekcije i prave veličine mnogokuta.
Zadatak 1: Odredite pravu veličinu trokuta \(\small\triangle ABC\) koji leži u 1. projicirajućoj ravnini.
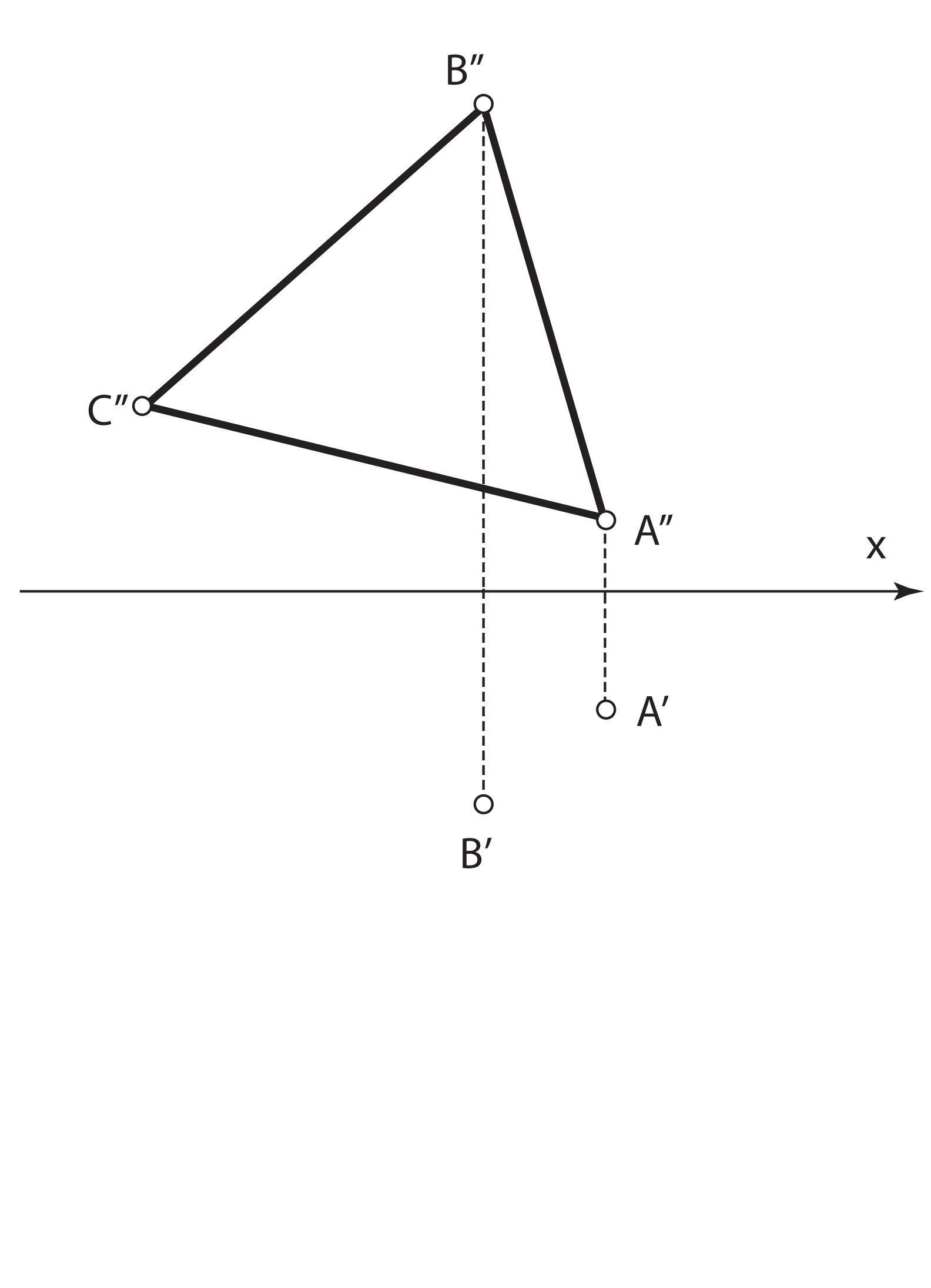
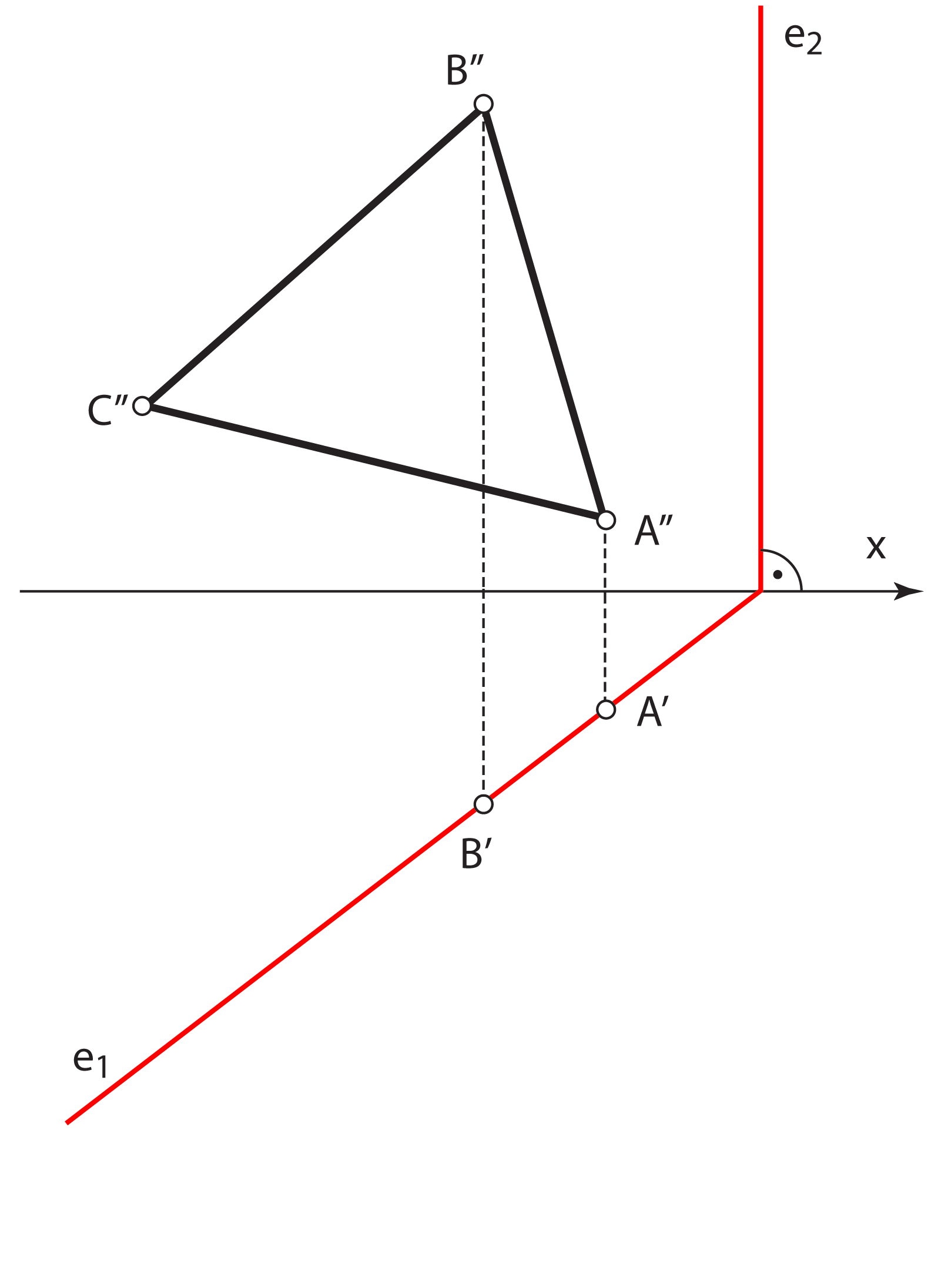
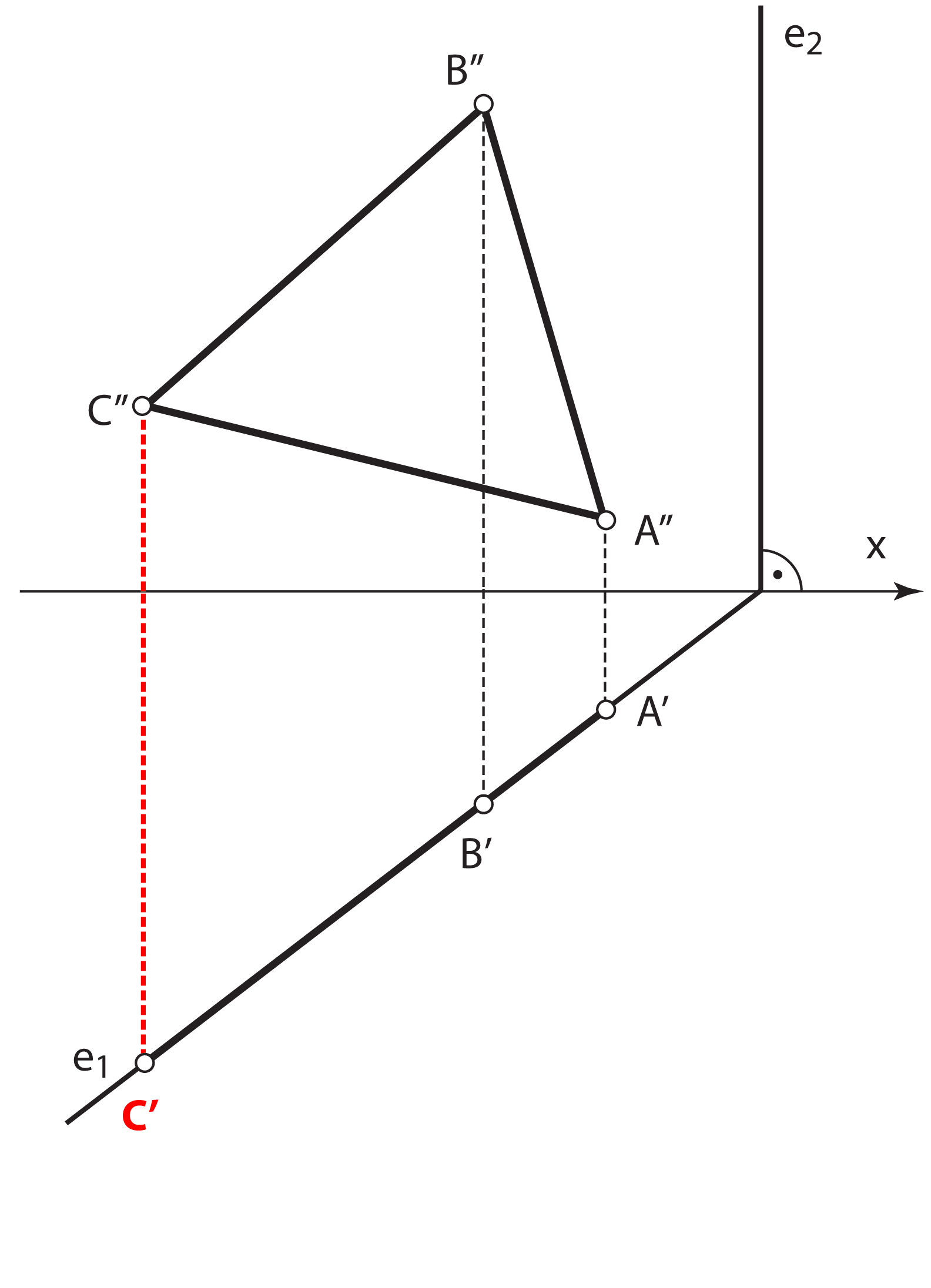
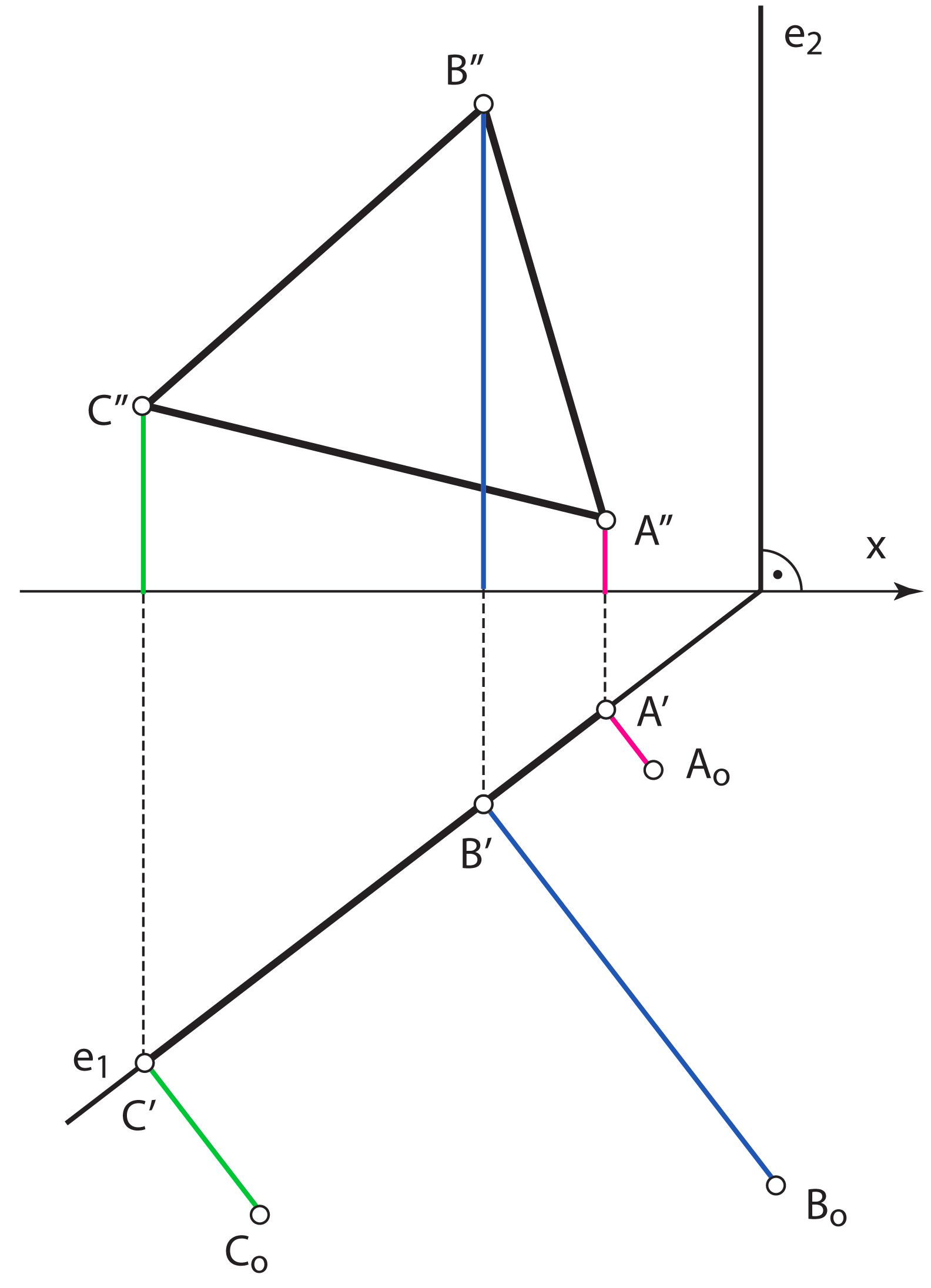
- Tlocrt točke \(\small C\) konstruiramo na temelju činjenice da zadani trokut leži u 1. projicirajućoj ravnini i da se u tlocrtu projicira u dužinu
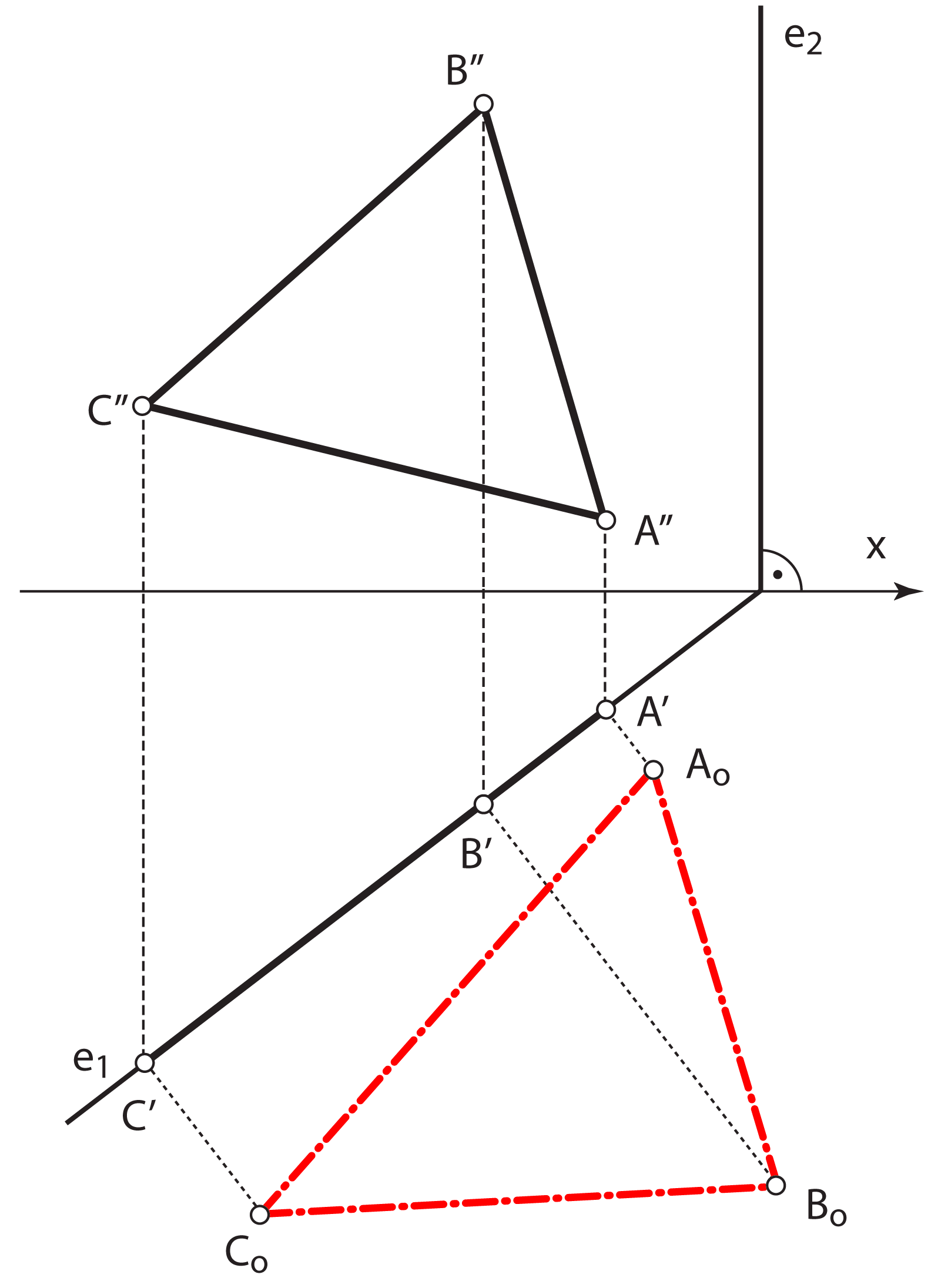
- Rotiramo točke \(\small A\), \(\small B\) i \(\small C\) oko prvog traga u ravninu \(\small \Pi_1\) u položaje \(\small A_\circ\), \(\small B_\circ\) i \(\small C_\circ\). U slučaju projicirajuće ravnine to je postupak koji smo već upoznali, a nazivamo ga i prevaljivanjem projicirajuće ravnine
- Konstruiramo trokut \(\small \triangle A_\circ B_\circ C_\circ\) koji je sukladan trokutu \(\small\triangle ABC\)
Zadatak 2: Odredite pravu veličinu paralelograma \(\small ABCD\) koji leži u 2. projicirajućoj ravnini.
Valja reći da ako poligon leži u ravnini koja je u općem položaju prema ravninama projekcije, tada na ovaj način nećemo moći konstruirati njemu sukladni poligon. Pokušajte za primjer riješiti sljedeći zadatak.
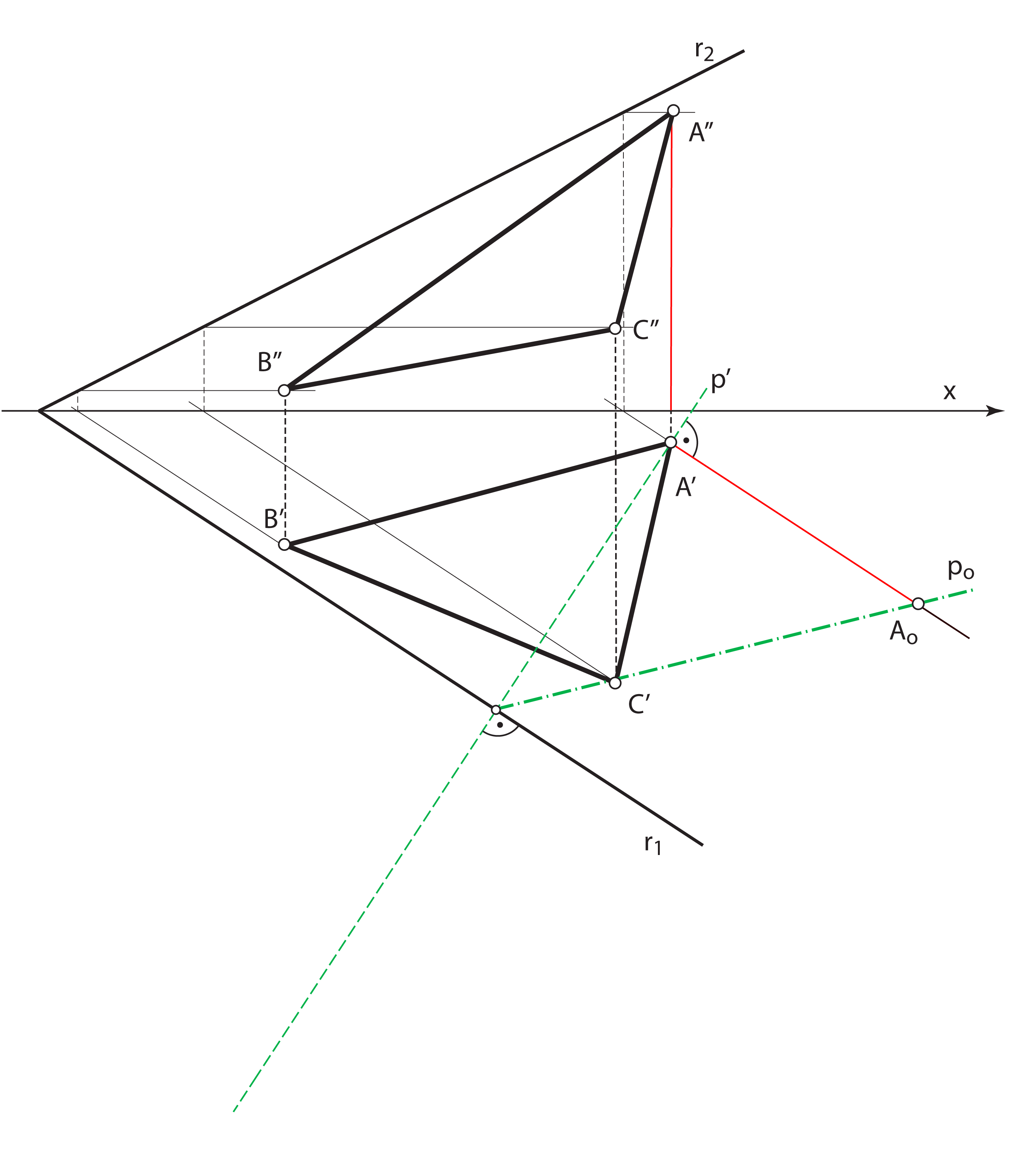
Zadatak 3: Odredite pravu veličinu trokuta \(\small\triangle ABC\) koji leži u ravnini \(\small\mathrm P\).
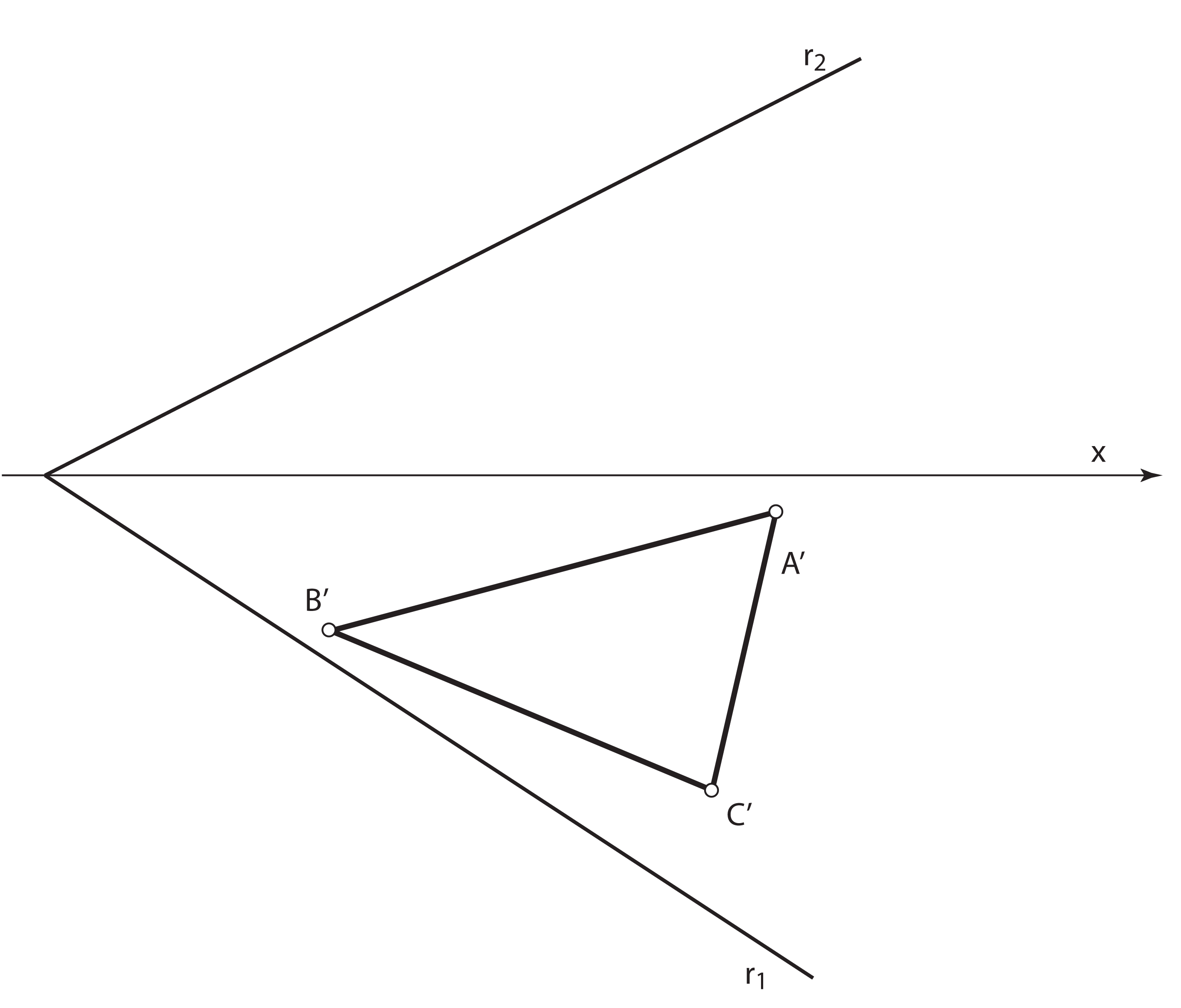
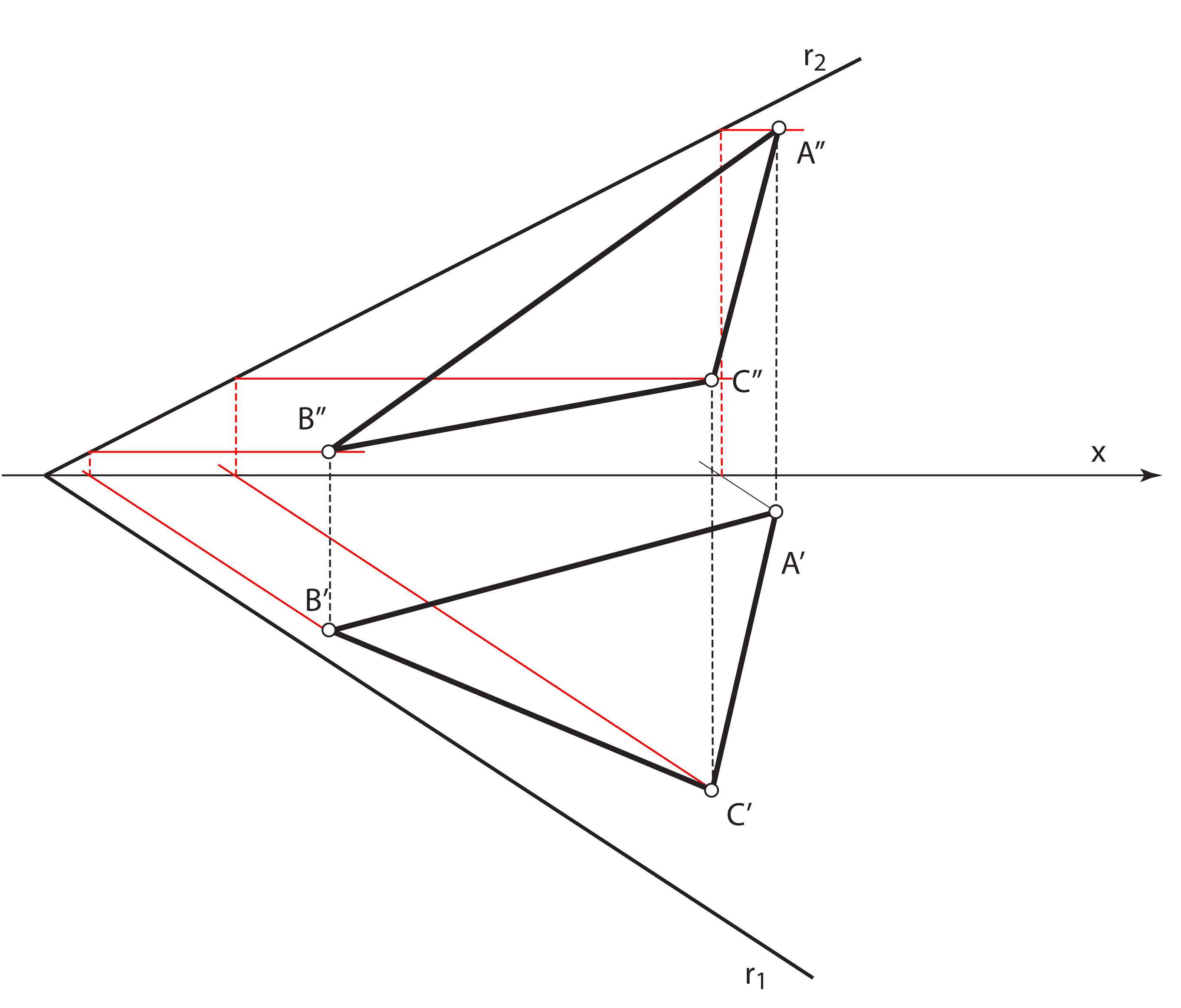
- Nacrt se trokuta konstruira na temelju činjenice da leži u ravnini \(\small\mathrm P\) – pomoću sutražnica 1. skupine
- Za daljnje rješavanje zadatka treba primijeniti postupak rotacije ravnine \(\small\mathrm P\) u jednu od ravnina projekcije
Rotacija ravnine oko traga
Ravninu \(\small\mathrm P\) rotiramo u ravninu \(\small \Pi_1\) oko njezinog 1. traga ili u ravninu \(\small \Pi_2\) oko njezinog 2. traga.
KONSTRUKCIJA točke u rotiranom položaju (rotacija oko 1. traga).
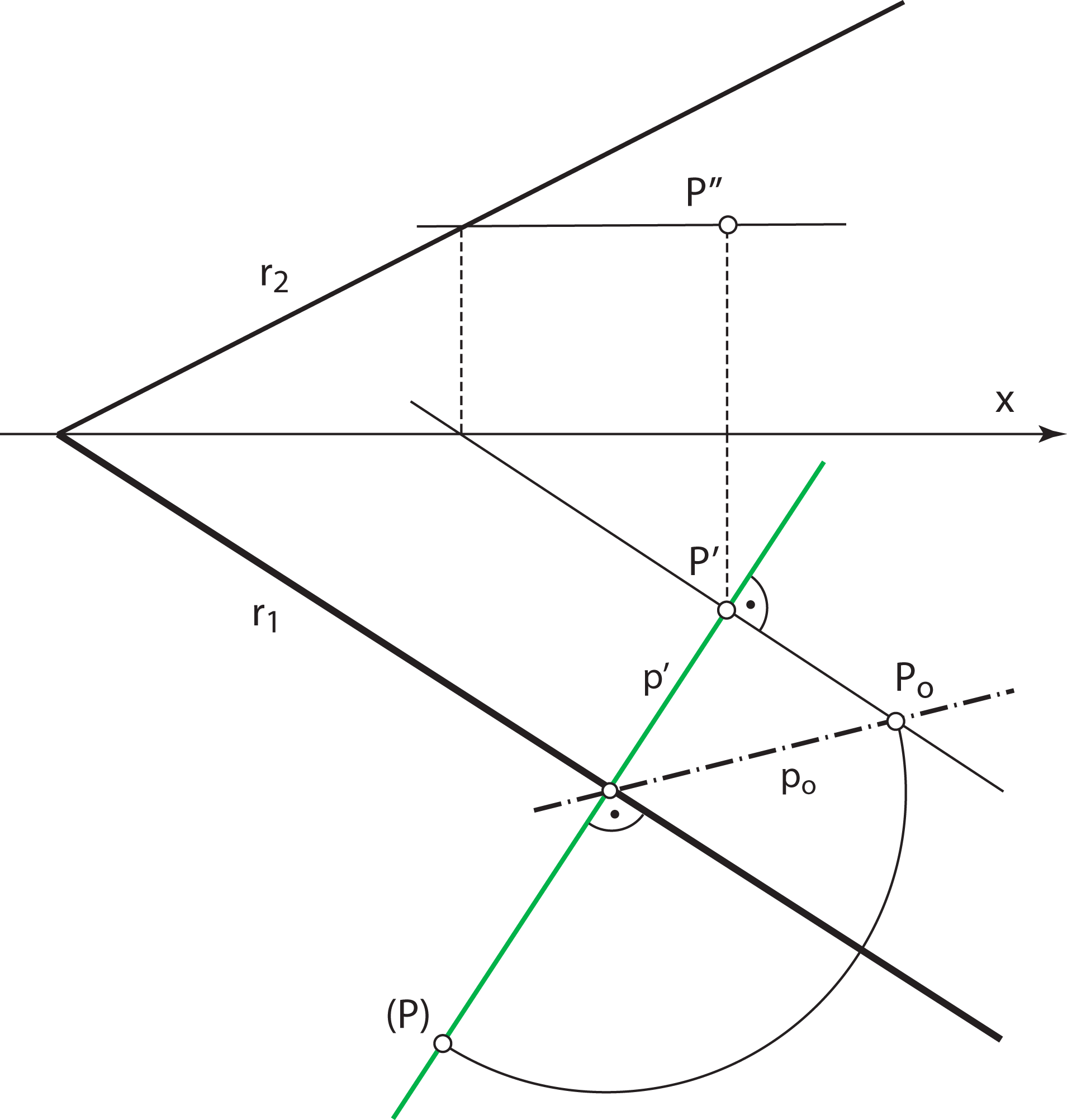
Sada možemo rotirati trokut i odrediti pravu veličinu trokuta iz zadatka 3.
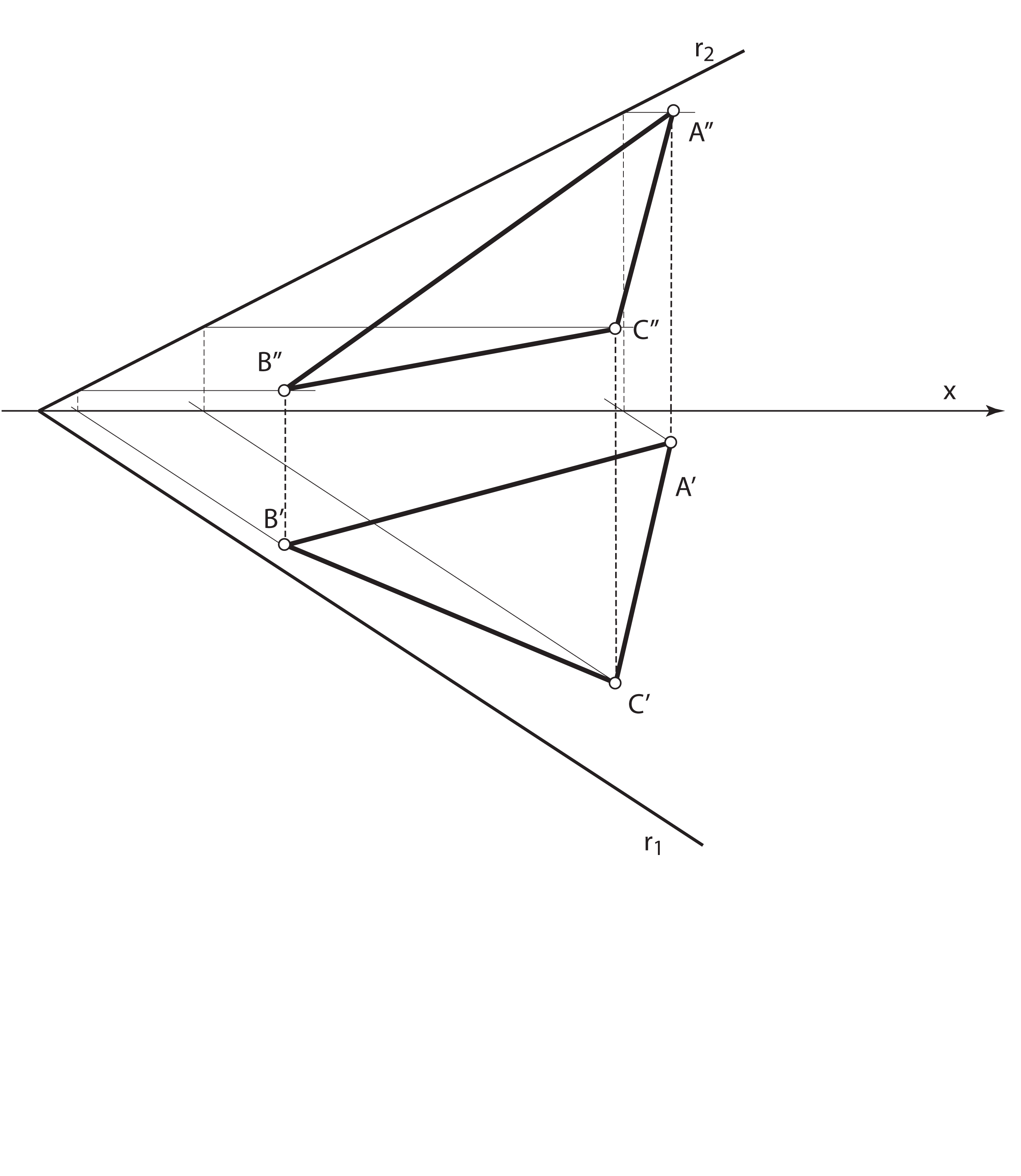
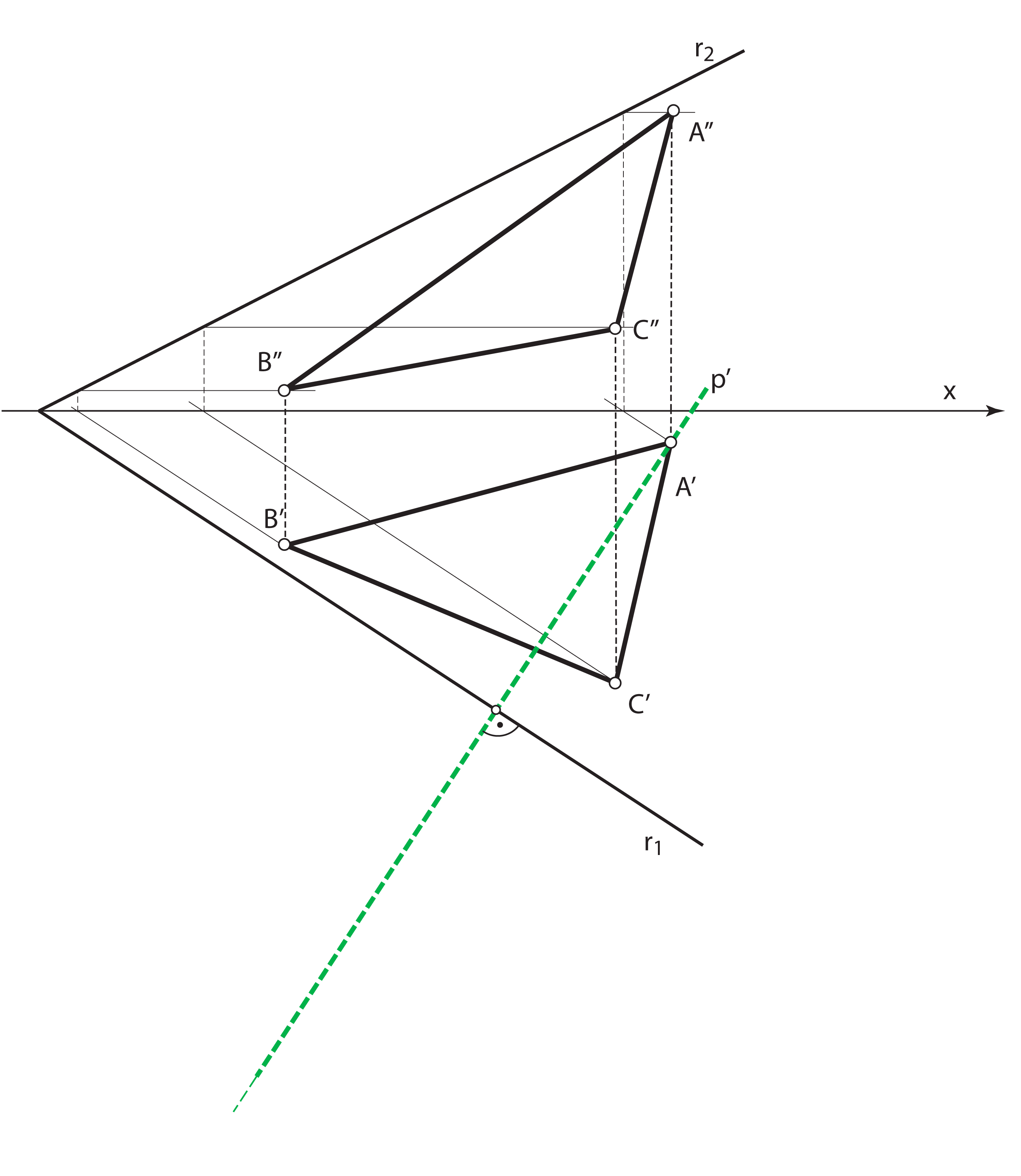
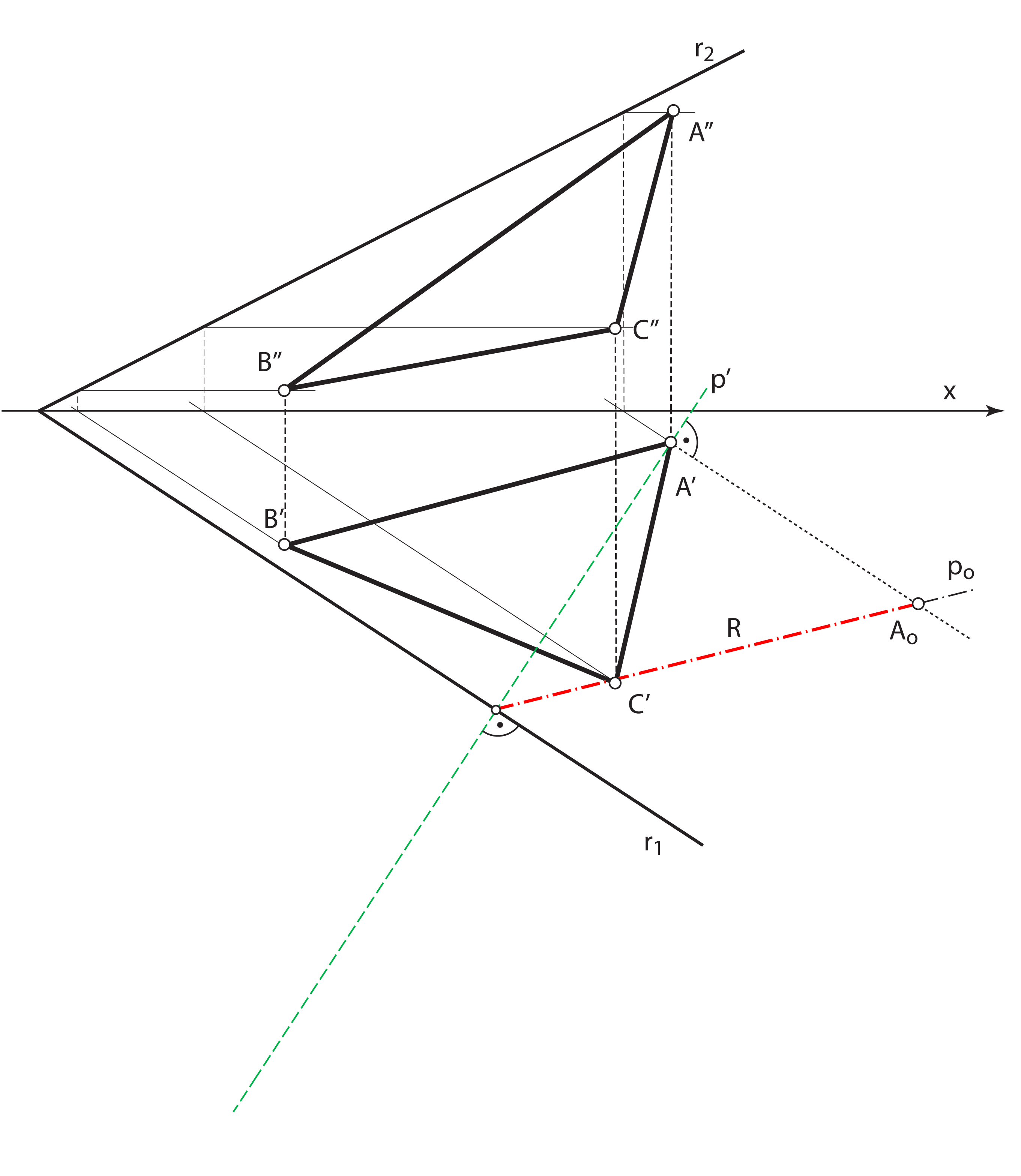
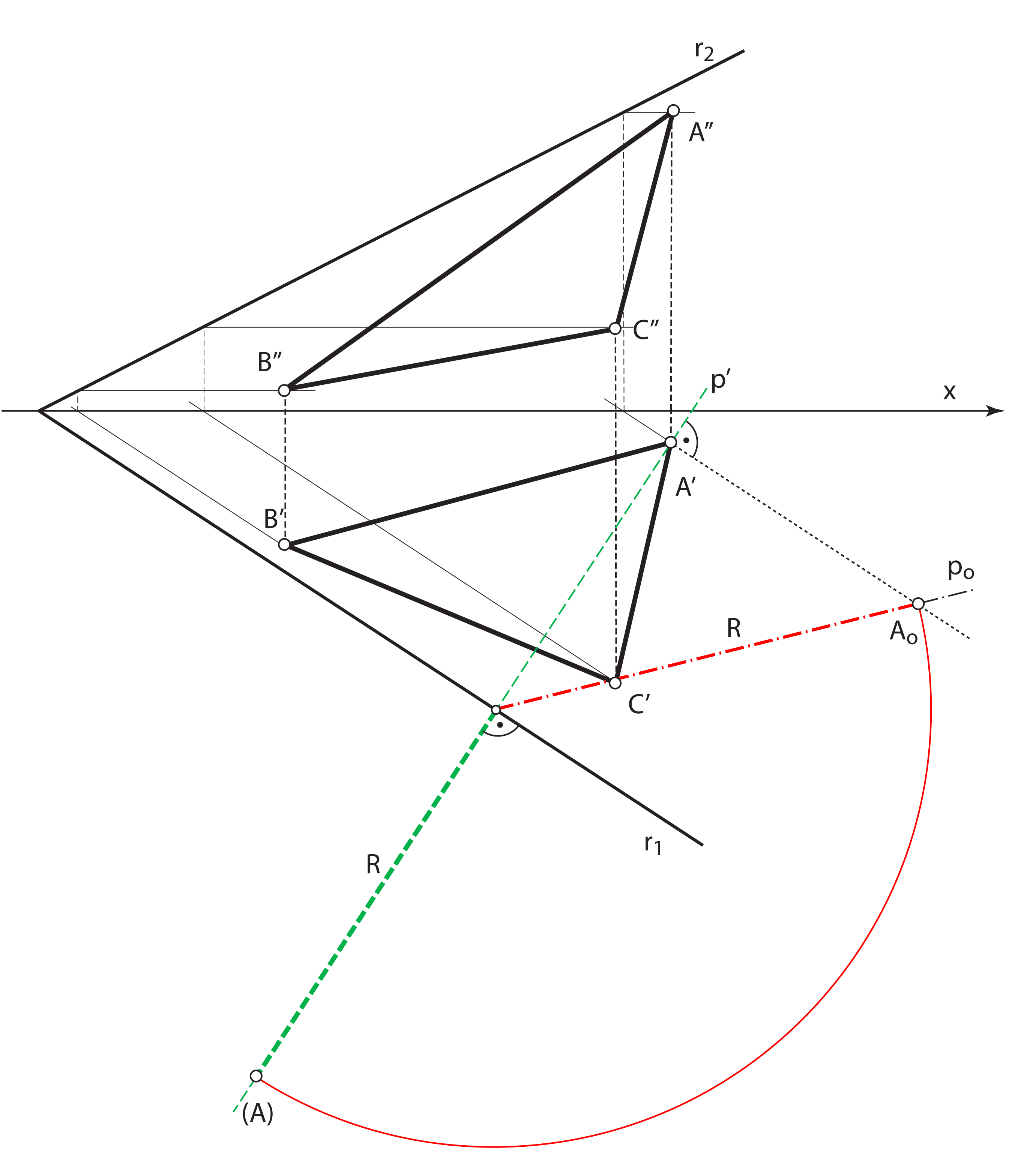
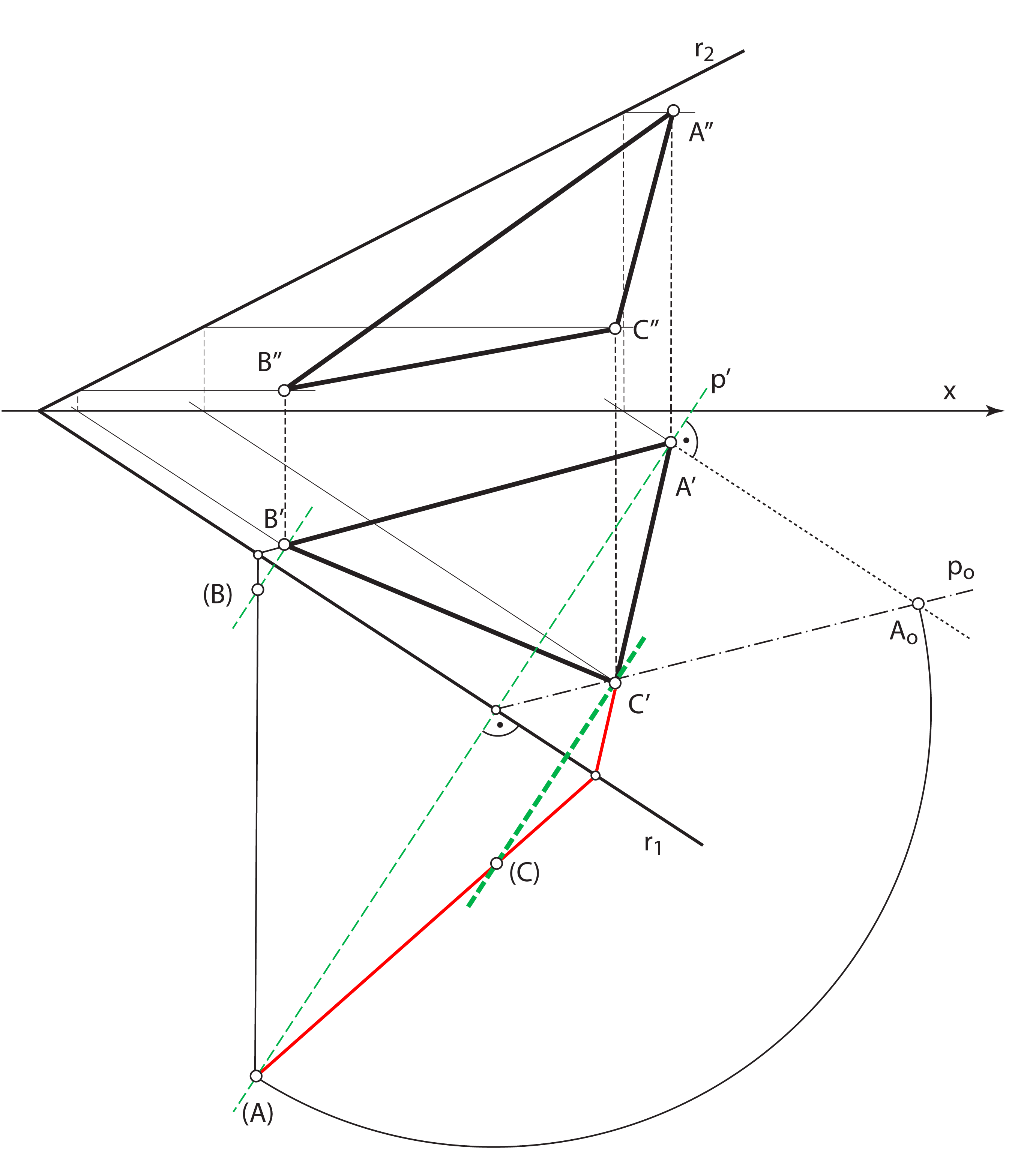
- Rotiramo točku \(\small A\) u ravninu \(\small \Pi_1\) oko 1. traga ravnine \(\small\mathrm P\)
- Dobivena točka \(\small (A)\) leži na tlocrtu one priklonice 1. skupine ravnine \(\small\mathrm P\) koja prolazi točkom \(\small A\)
- Polumjer rotacije točke \(\small A\) jednak je njezinoj udaljenosti od traga \(\small r_1\)
Uočite sljedeće:
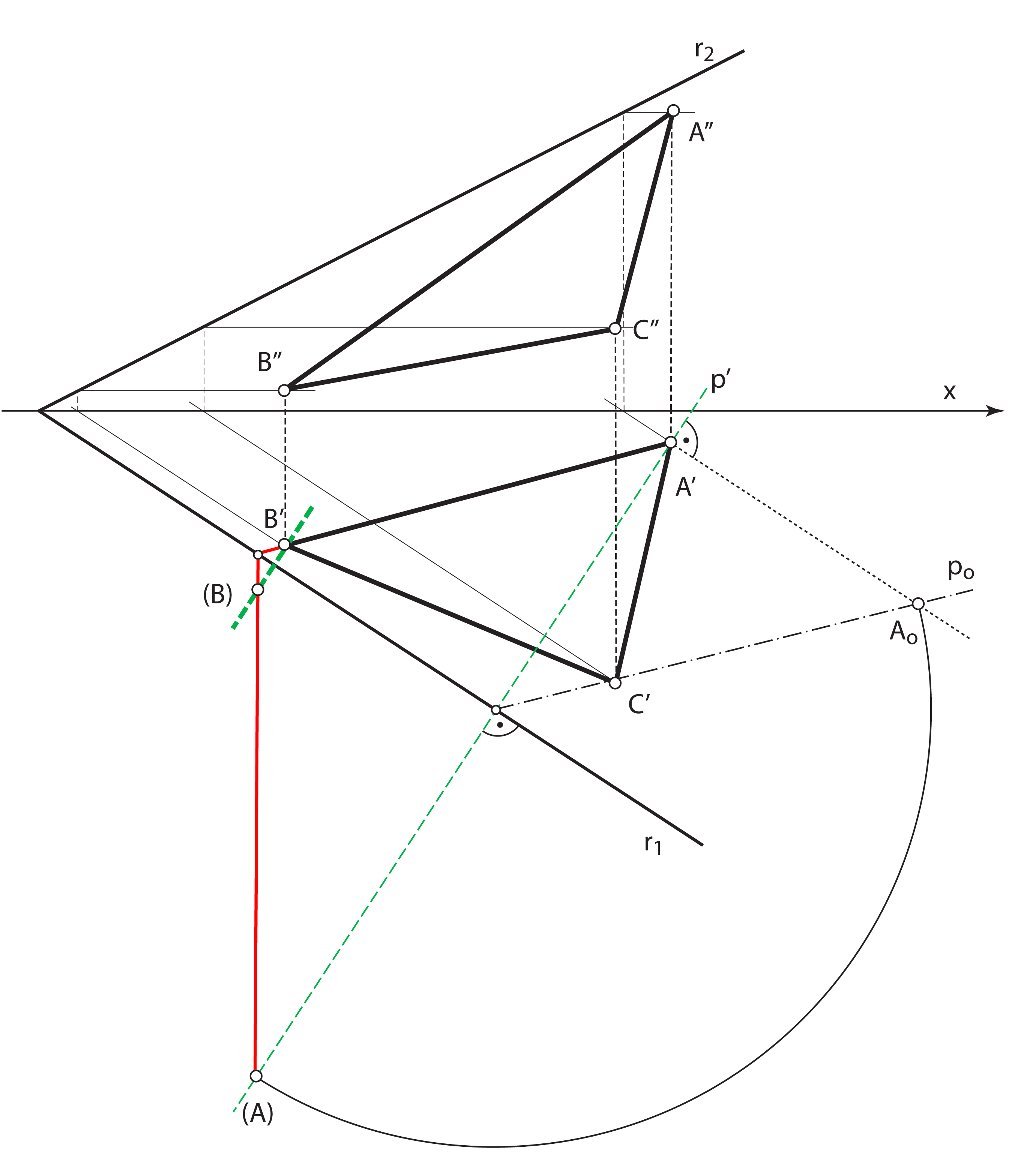
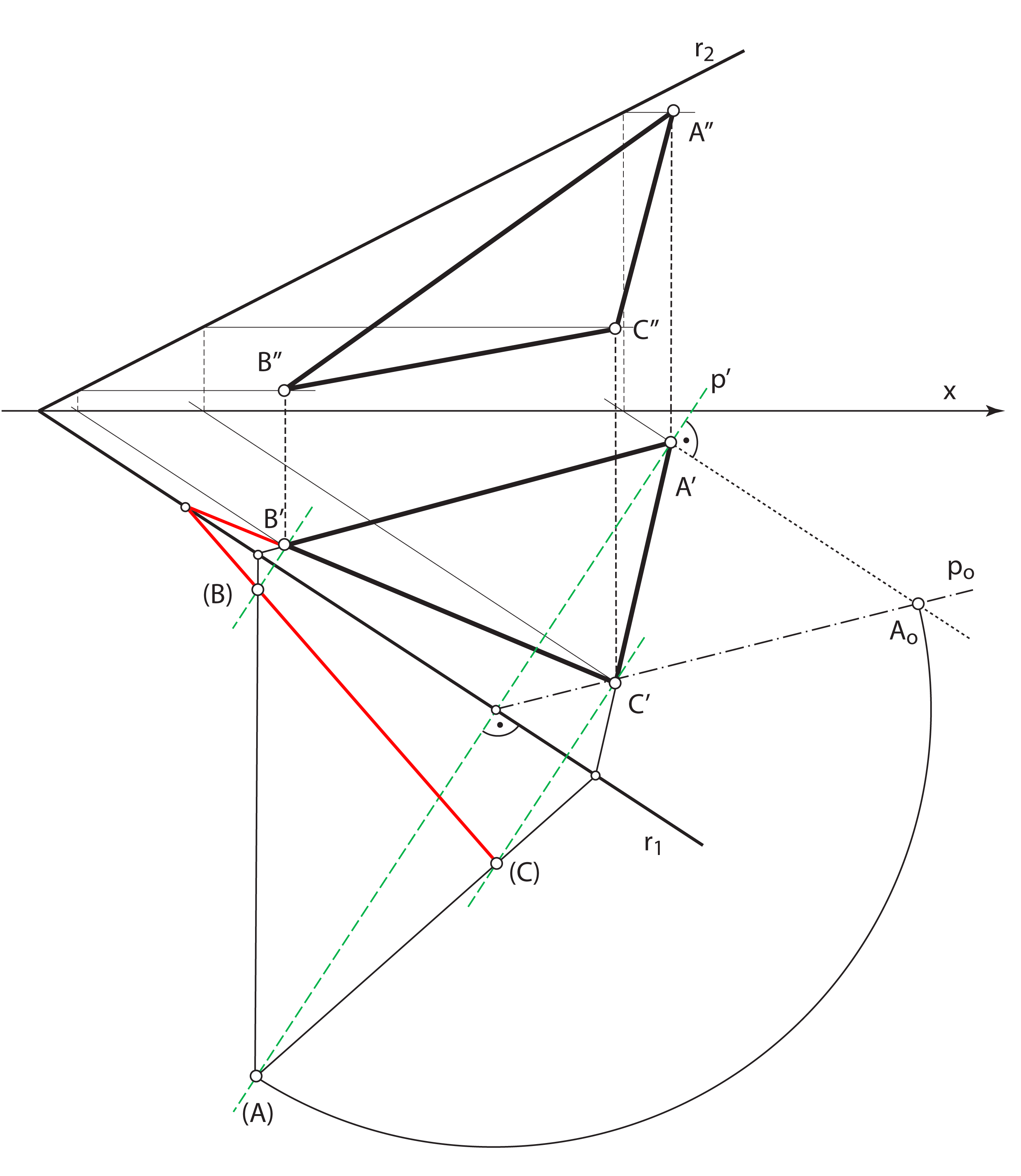
- Tlocrti točaka i pravaca ravnine \(\small\mathrm P\) preslikavaju se u njihove rotirane položaje u ravnini \(\small \Pi_1\) afinom transformacijom. Os tog afiniteta je trag \(\small r_1\), a zrake su tlocrti priklonica 1. skupine ravnine \(\small\mathrm P\)
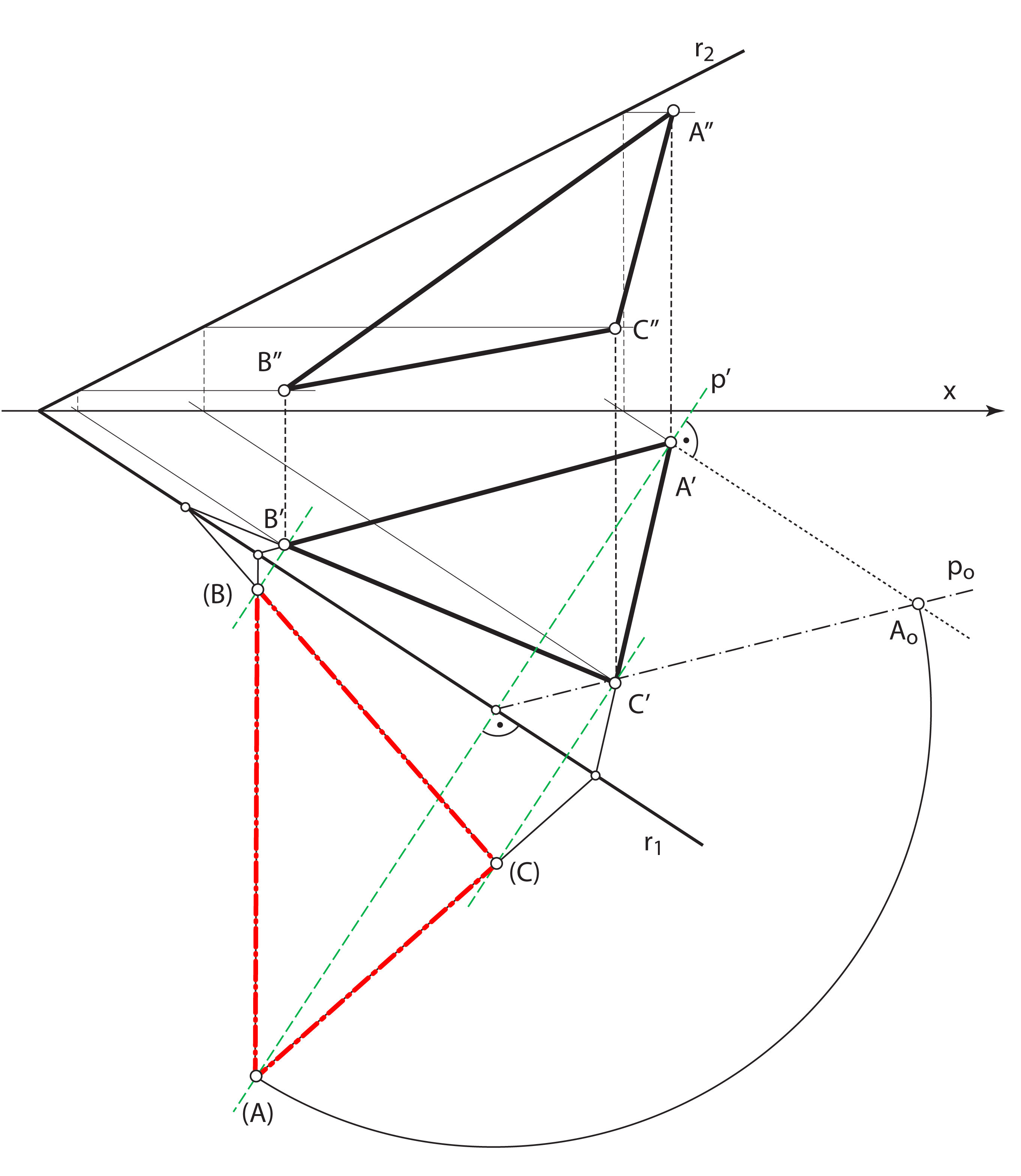
- U afinitetu \(\small (A',(A),r_1)\) konstruiramo točke \(\small (B)\) i \(\small (C)\)
- Trokut \(\small \triangle (A)(B)(C)\) sukladan je trokutu \(\small\triangle ABC\)
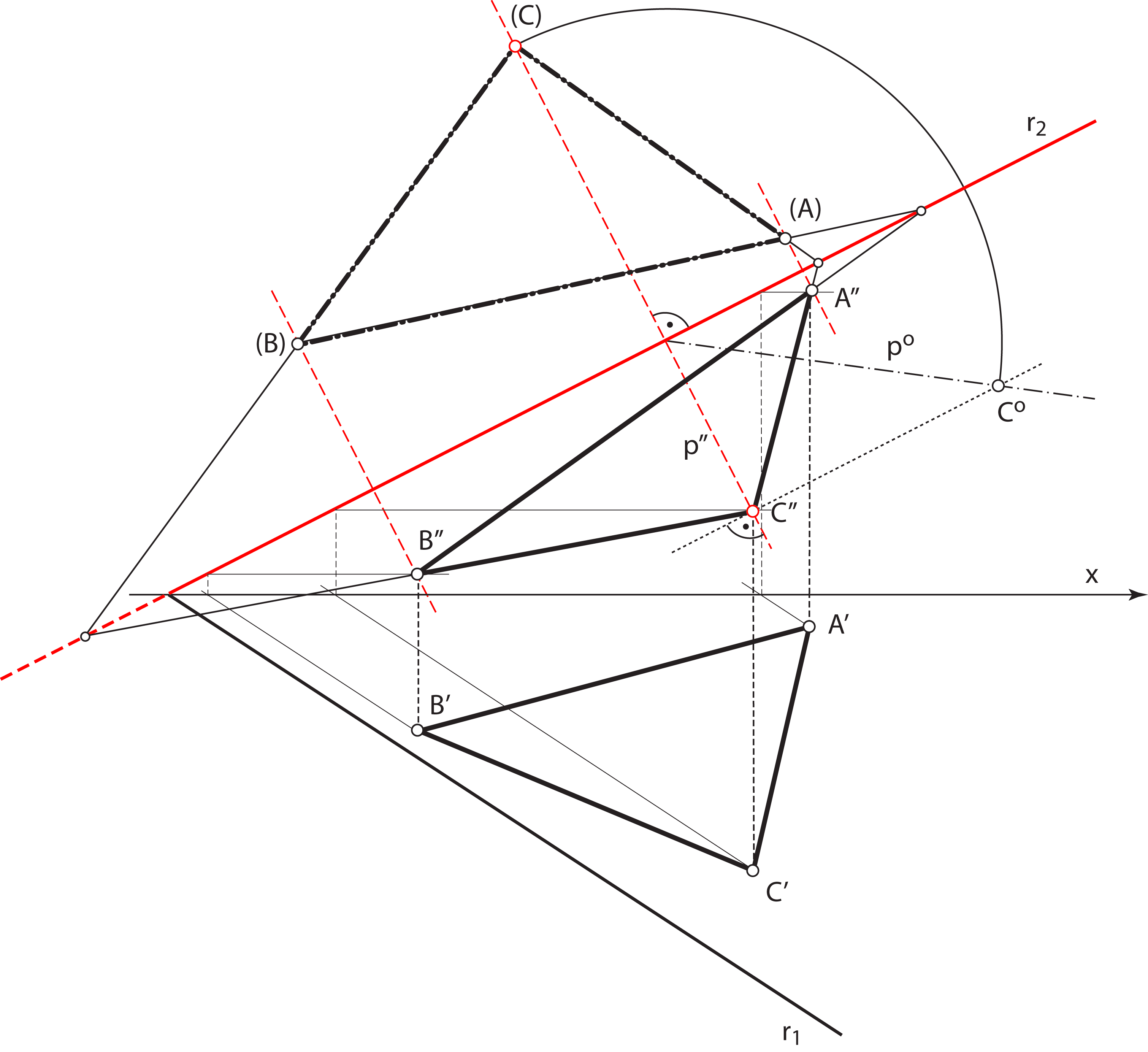
Analogni se zaključci mogu izvesti za rotaciju opće ravnine oko njezinog 2. traga u ravninu \(\small \Pi_2\). U tom je slučaju afina veza uspostavljena između nacrta elemenata ravnine \(\small\mathrm P\) i njihovih rotiranih položaja u ravnini \(\small \Pi_2\). Os tog afiniteta je 2. trag ravnine \(\small\mathrm P\), a zrake su nacrti priklonica 2. skupine te ravnine.
Projiciranje kružnice
Ako kružnica \(\small k\) leži u ravnini \(\small\mathrm P\) koja je u općem položaju prema ravnini projekcije \(\small\Pi\), njezina je ortogonalna projekcija na tu ravninu elipsa \(\small k'\).
Kako se pri ortogonalnom projiciranju čuvaju omjeri dužina i paralelnost, vrijedi sljedeće:
- Središte kružnice \(\small k\) projicira se u središte elipse \(\small k'\)
- Promjeri kružnice projiciraju se u promjere njezine projekcije
- Parovi ortogonalnih promjera kružnice projiciraju se u parove konjugiranih promjera projekcije
PITANJE: Koji se par ortogonalnih promjera kružnice \(\small k\) projicira u veliku i malu os elipse \(\small k'\)?
Pri ortogonalnom projiciranju dužine njezina se duljina skraćuje ili ostaje ista u slučaju kada je dužina paralelna s ravninom projekcije.
Stoga se promjer kružnice koji je paralelan s ravninom projekcije projicira u najdulji promjer njezine projekcije, dakle u njezinu veliku os.
Budući da je mala os elipse okomita na njezinu veliku os, mala os projekcije kružnice leži na pravcu koji je okomit na pravac velike osi. To je ujedno pravac ravnine kružnice koji zatvara najveći kut s ravninom projekcije pa se dužine koje leže na tom pravcu najviše prikraćuju prilikom projiciranja.
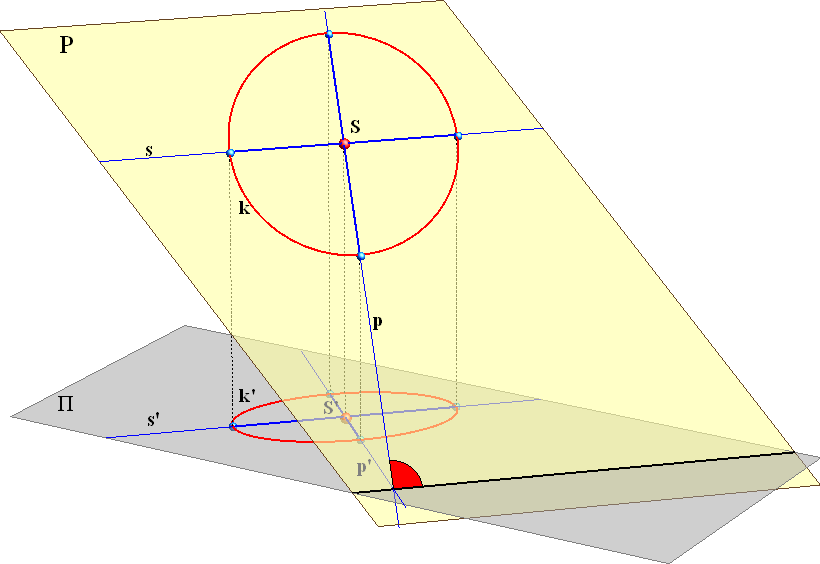
Možemo zaključiti sljedeće:
- Velika os ortogonalne projekcije kružnice leži na projekciji odgovarajuće sutražnice njezine ravnine koja prolazi kroz projekciju središta, a njezina je duljina jednaka duljini promjera kružnice
- Mala os ortogonalne projekcije kružnice leži na projekciji odgovarajuće priklonice ravnine kružnice koja prolazi kroz projekciju središta
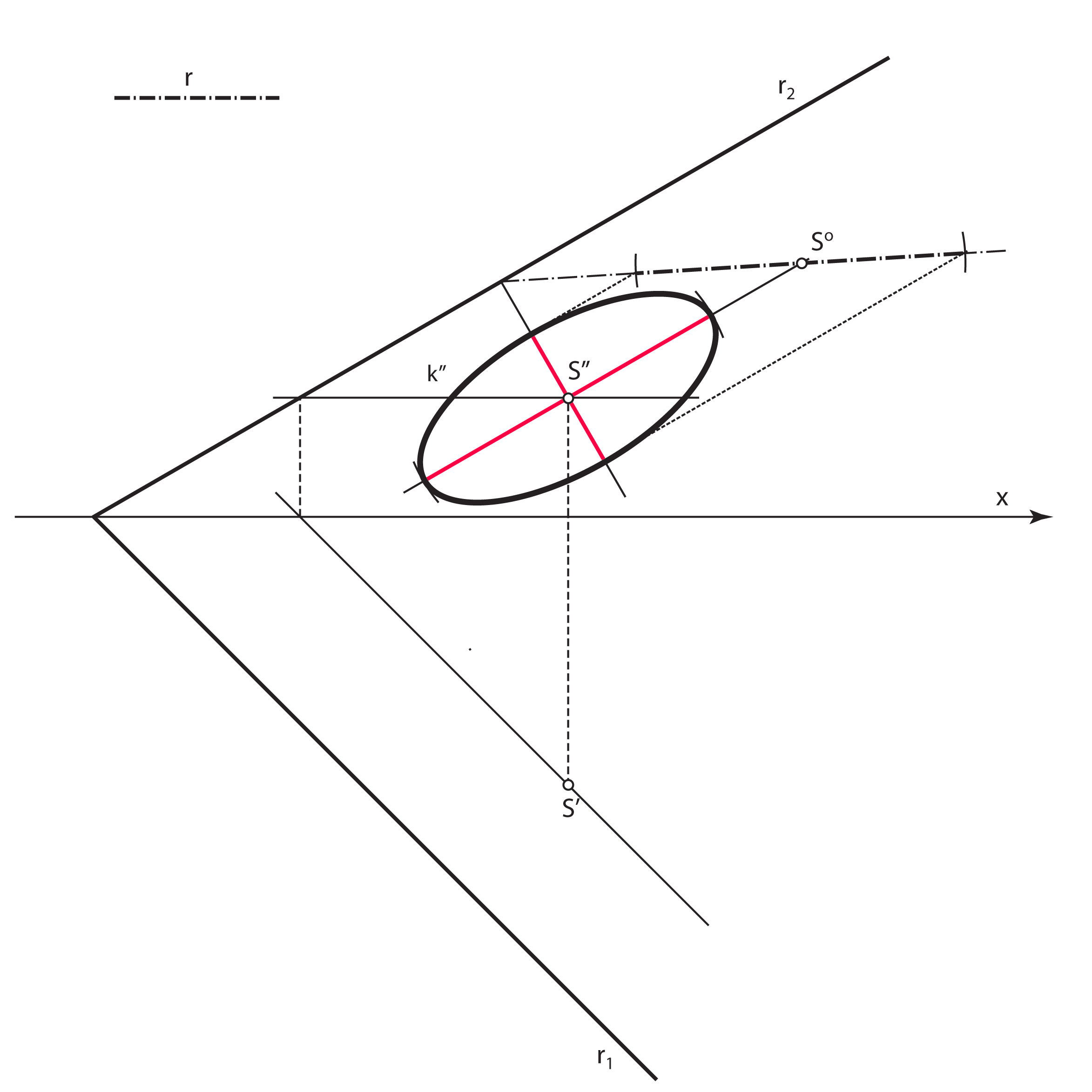
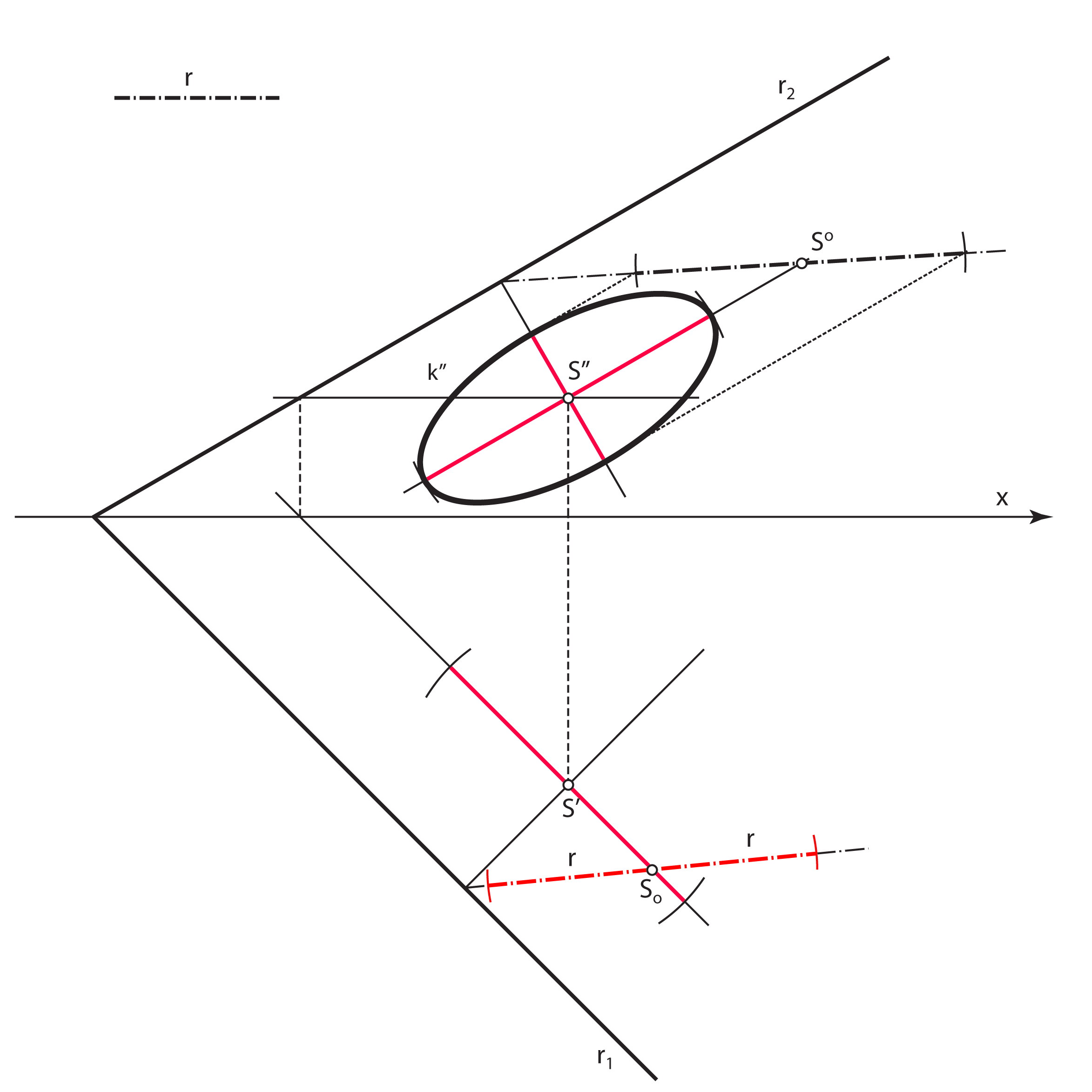
Zadatak 4: Konstruirajte tlocrt i nacrt kružnice \(\small k\) koja leži u zadanoj ravnini \(\small\mathrm P\), ako joj je točka \(\small S\) središte, a \(\small r\) polumjer.
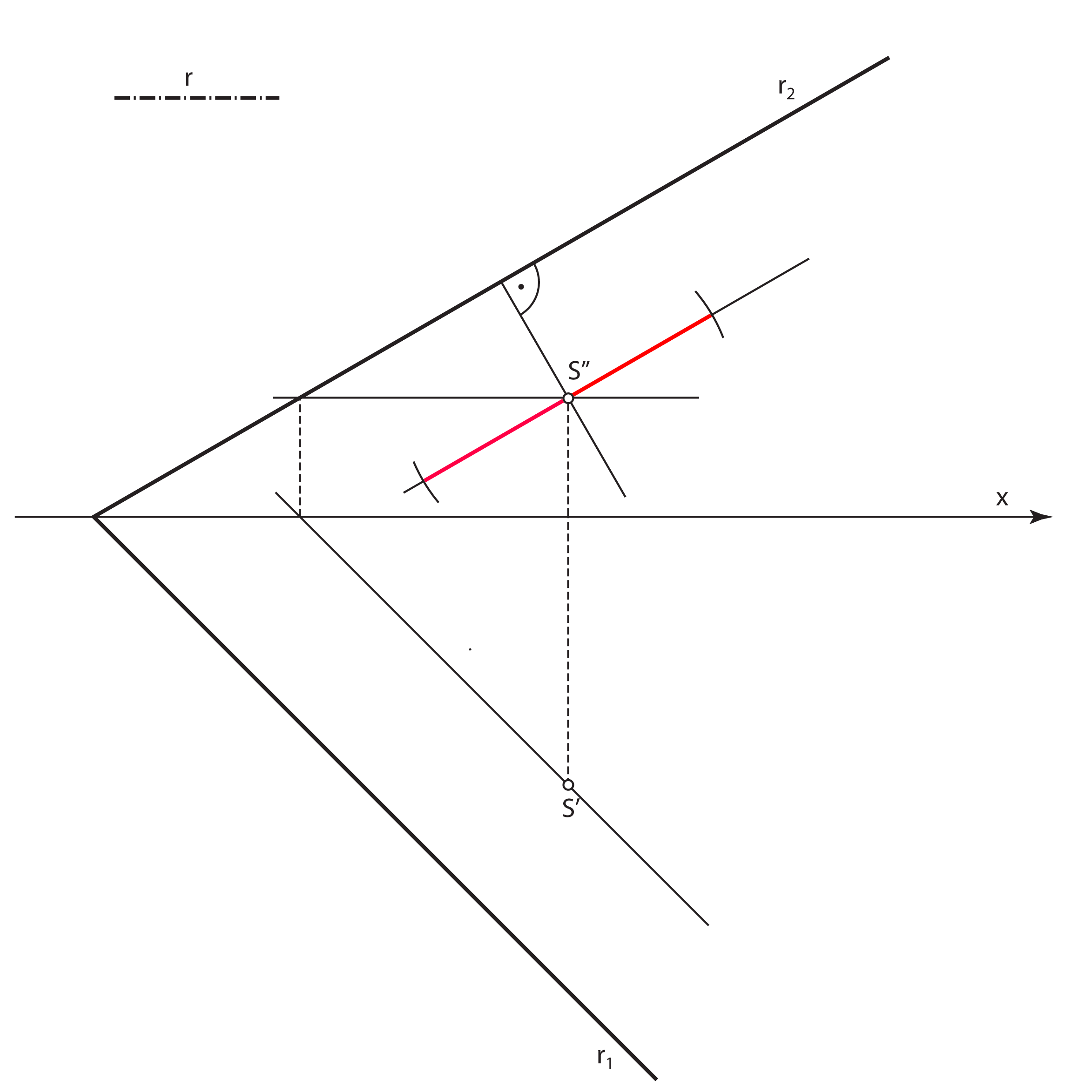
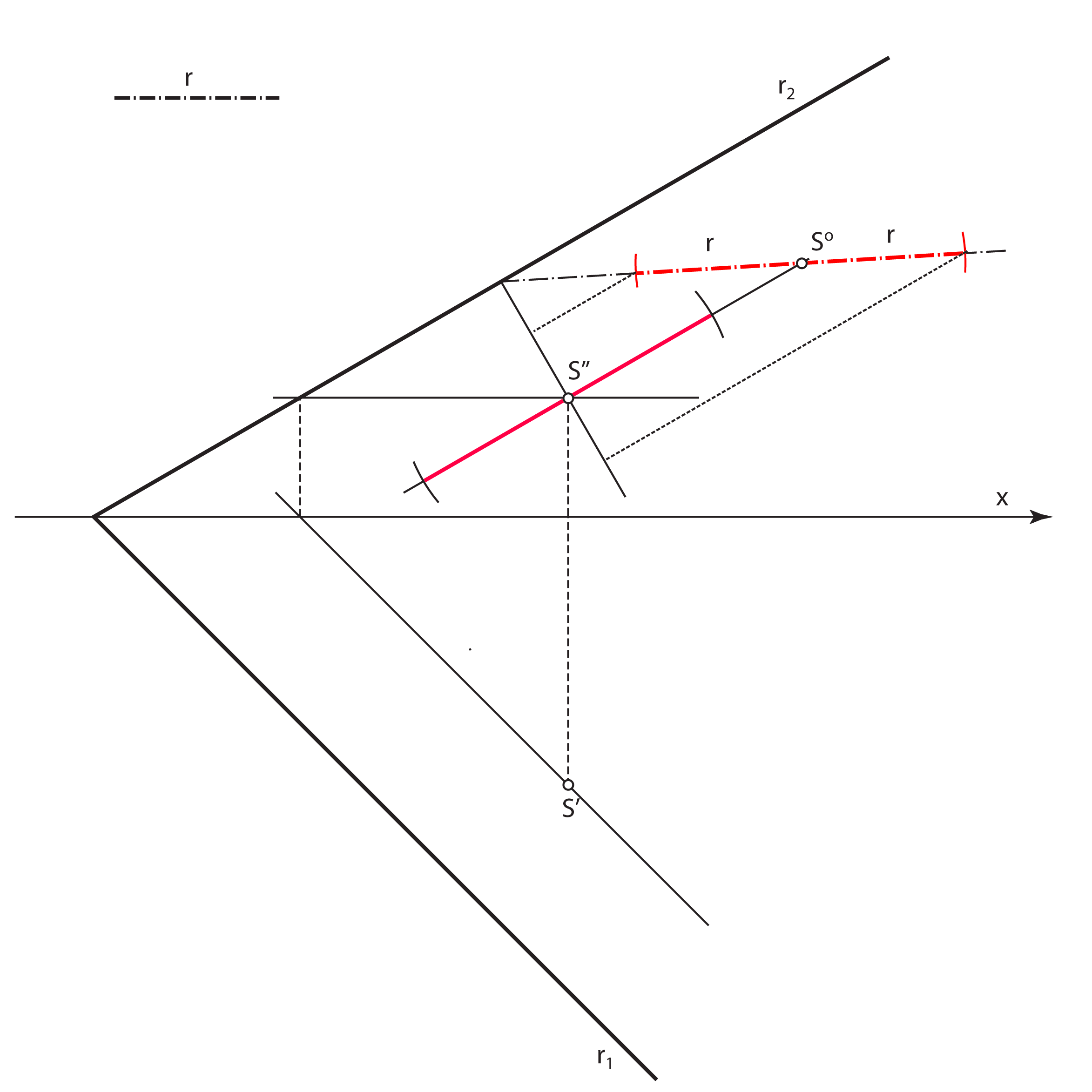
- Velika os nacrta kružnice \(\small k\) (velika os elipse \(\small k''\)) leži na nacrtu sutražnice 2. skupine ravnine \(\small\mathrm P\) kroz točku \(\small S''\), a duljina joj je \(\small 2r\)
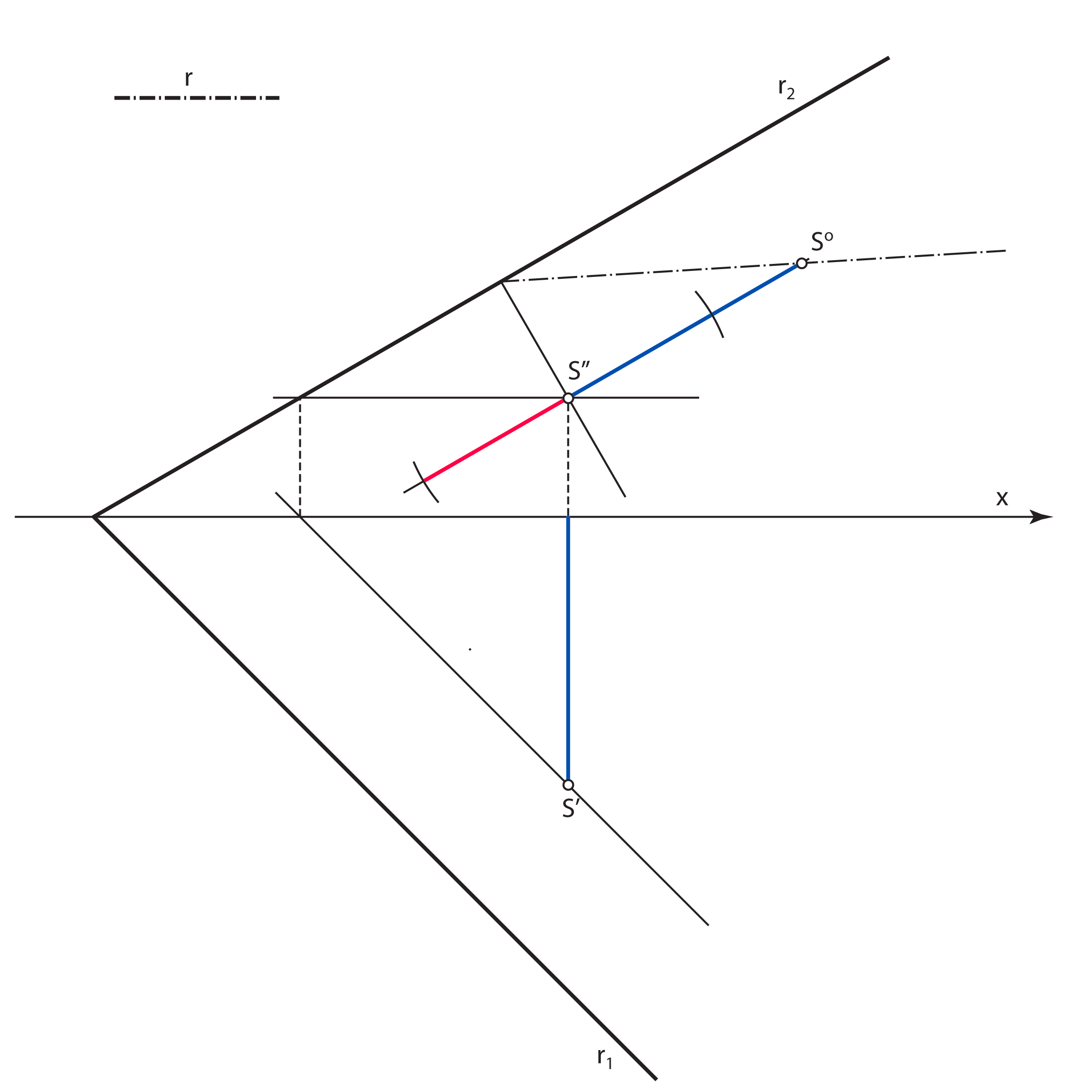
- Mala os nacrta kružnice \(\small k\) (mala os elipse \(\small k''\)) leži na nacrtu priklonice 2. skupine ravnine \(\small\mathrm P\) kroz točku \(\small S''\). Konstruira se tako da se ta priklonica prevali u ravninu \(\small \Pi_2\) i na nju nanese prava veličina promjera kružnice
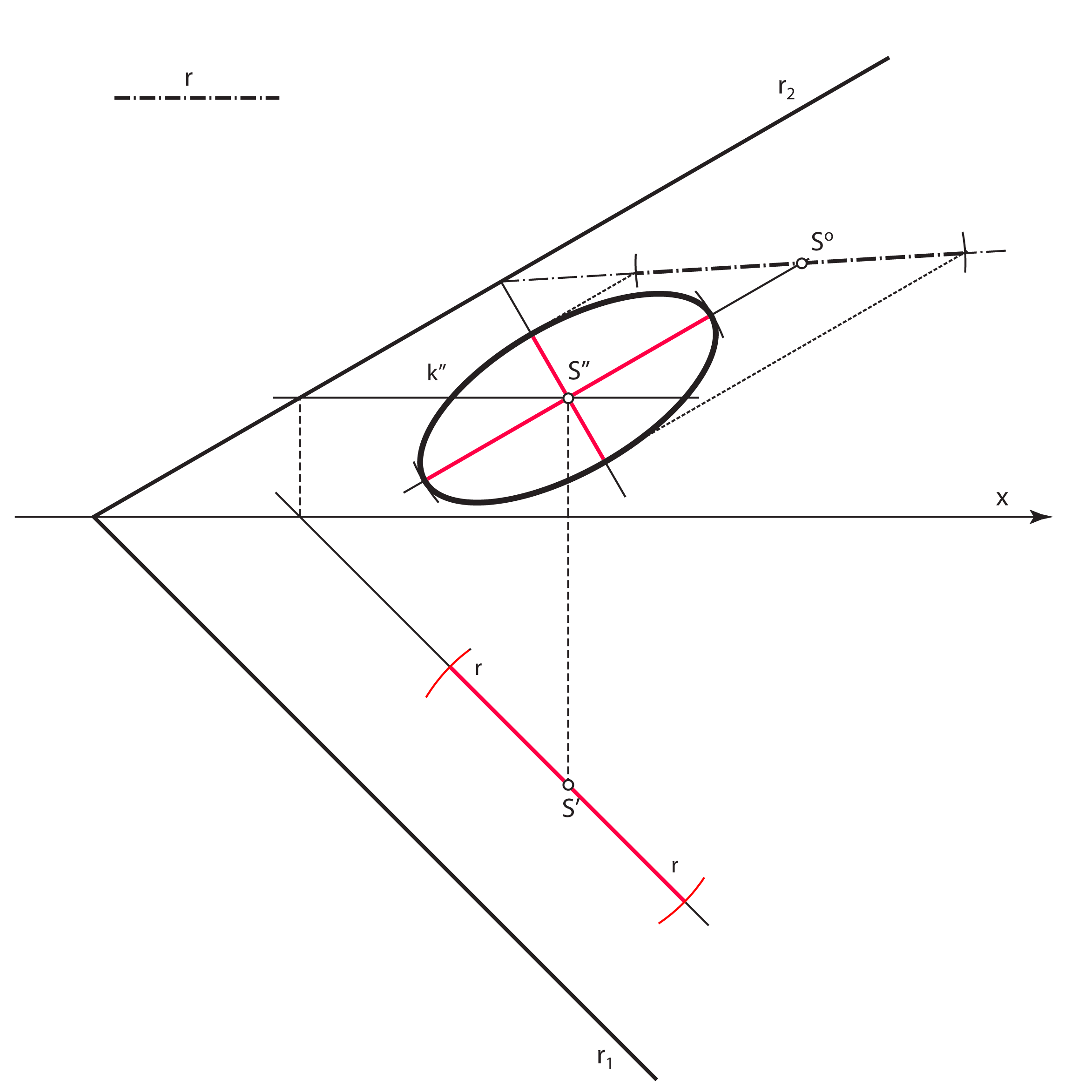
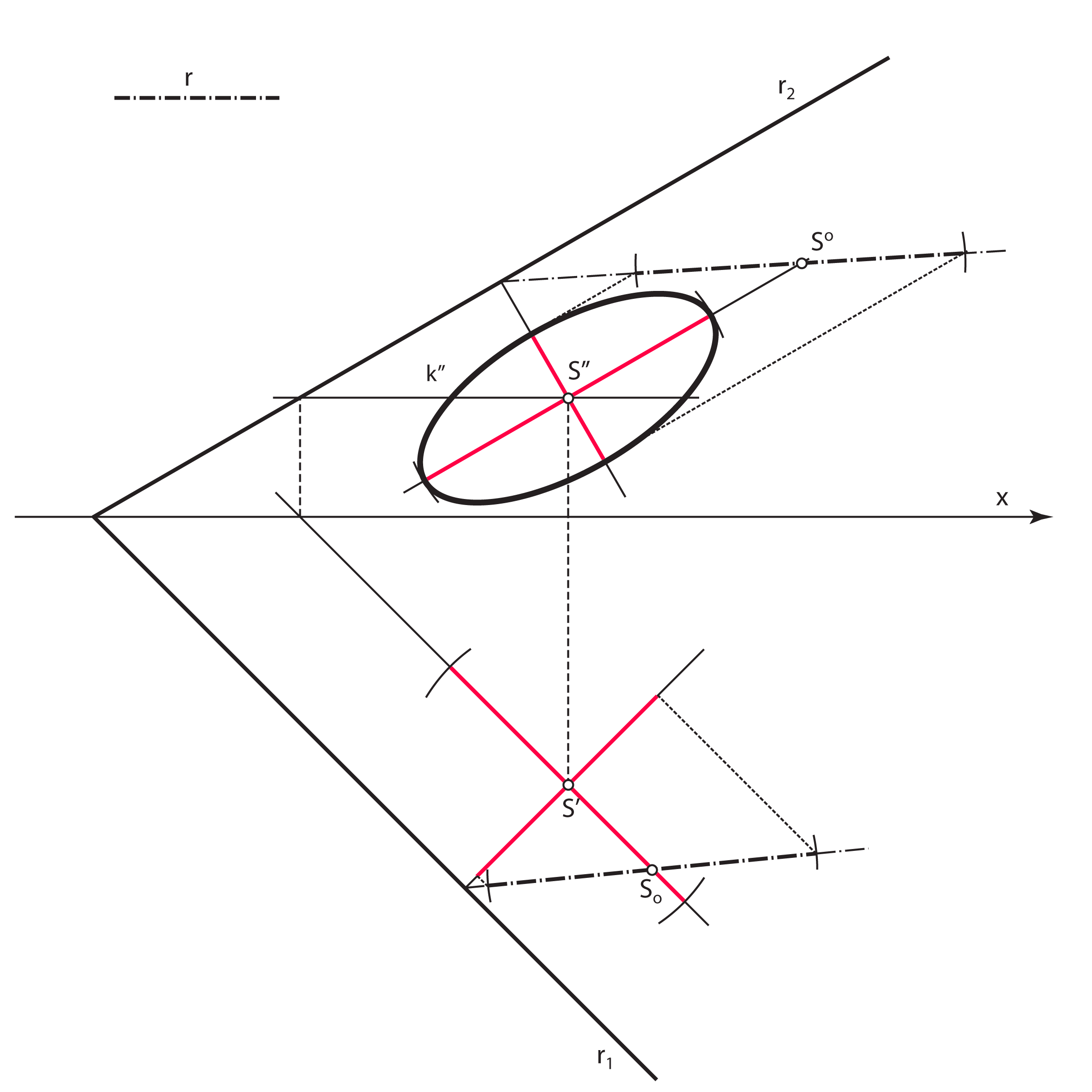
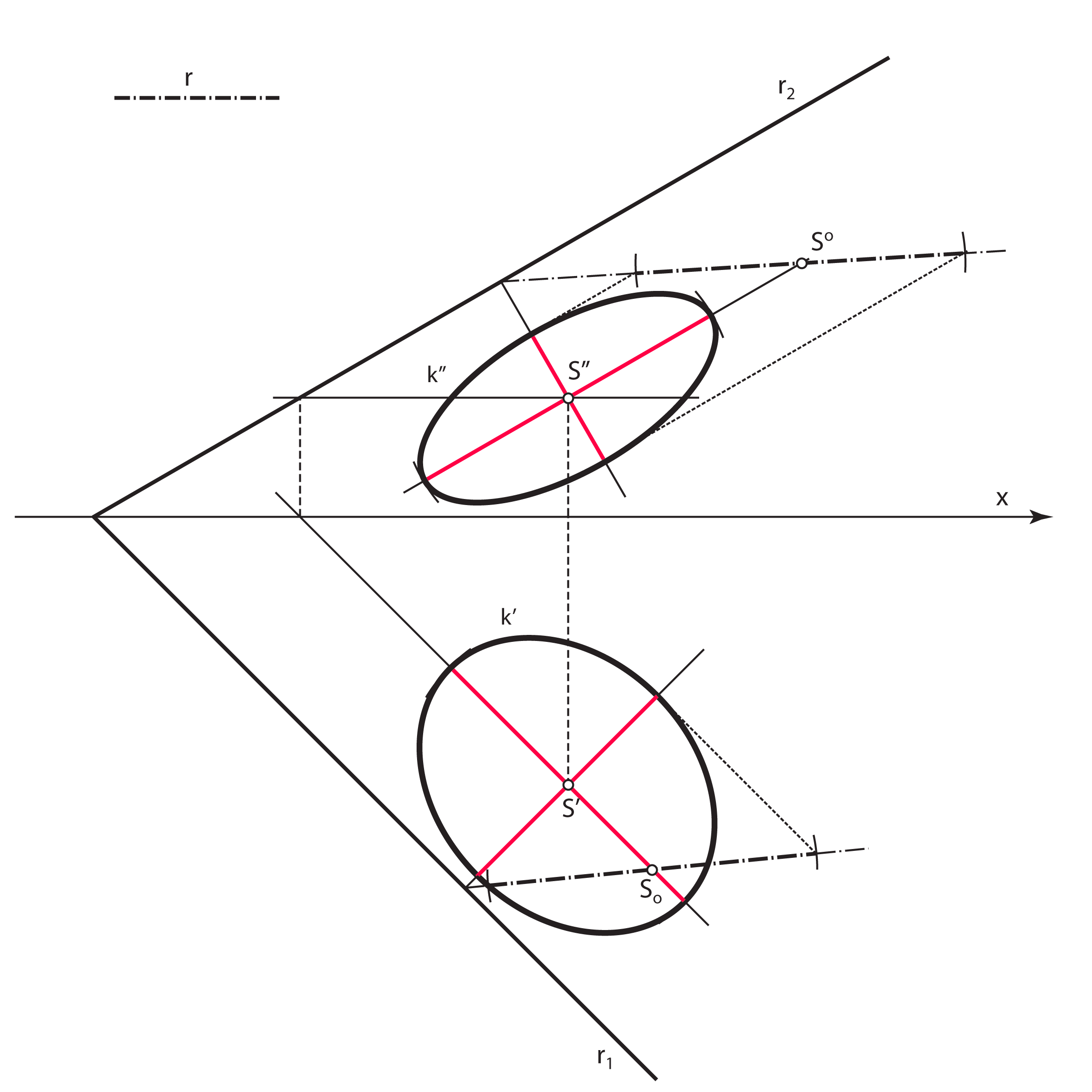
Slično vrijedi za konstrukciju velike i male osi tlocrtne elipse.
- Velika os tlocrta kružnice \(\small k\) (velika os elipse \(\small k'\)) leži na tlocrtu sutražnice 1. skupine ravnine \(\small\mathrm P\) kroz točku \(\small S'\), a duljina joj je \(\small 2r\)
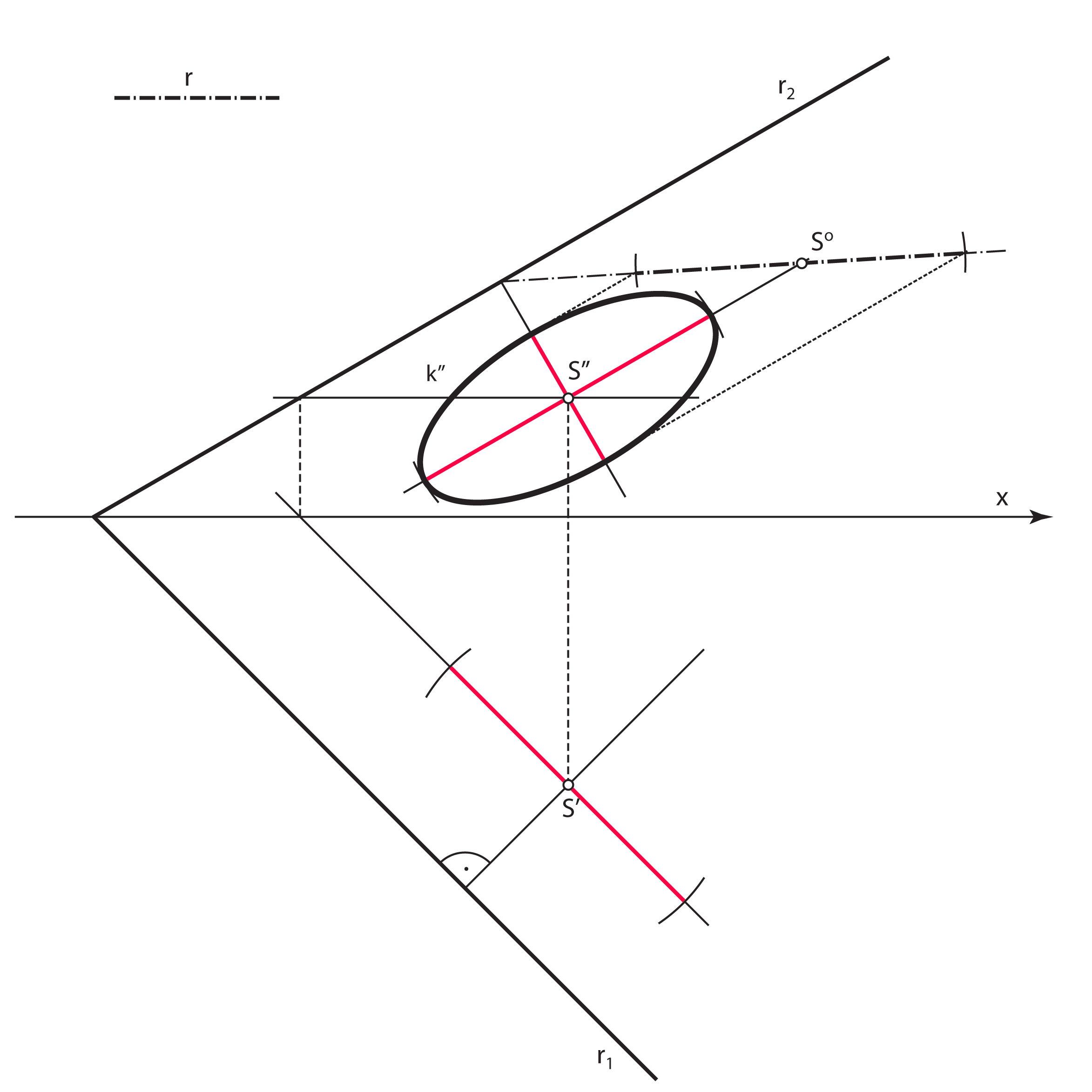
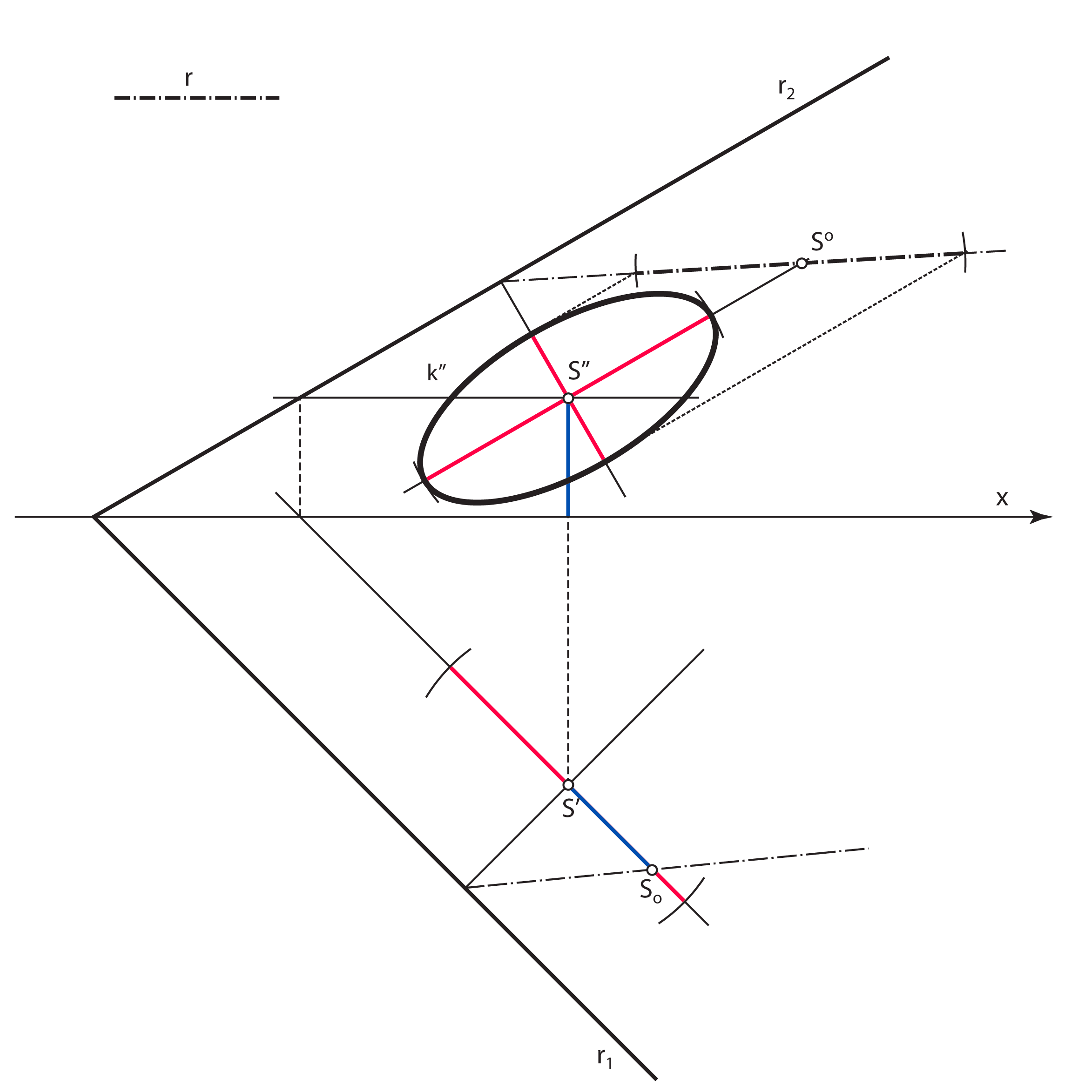
- Mala os tlocrta kružnice \(\small k\) (mala os elipse \(\small k'\)) leži na tlocrtu priklonice 1. skupine ravnine \(\small\mathrm P\) kroz točku \(\small S'\). Konstruira se tako da se ta priklonica prevali u ravninu \(\small \Pi_1\) i na nju nanese prava veličina promjera kružnice
Vidi prezentaciju 34.
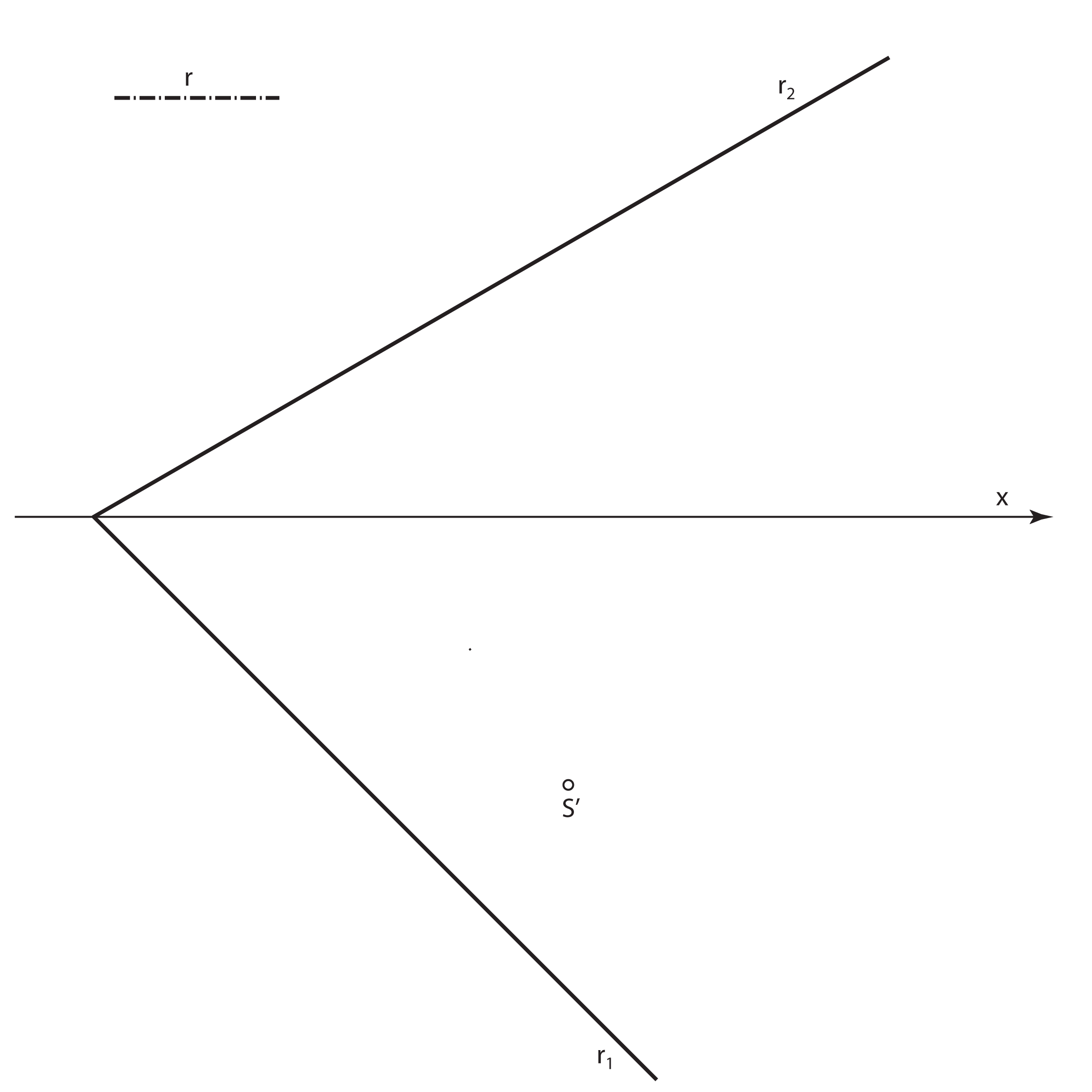
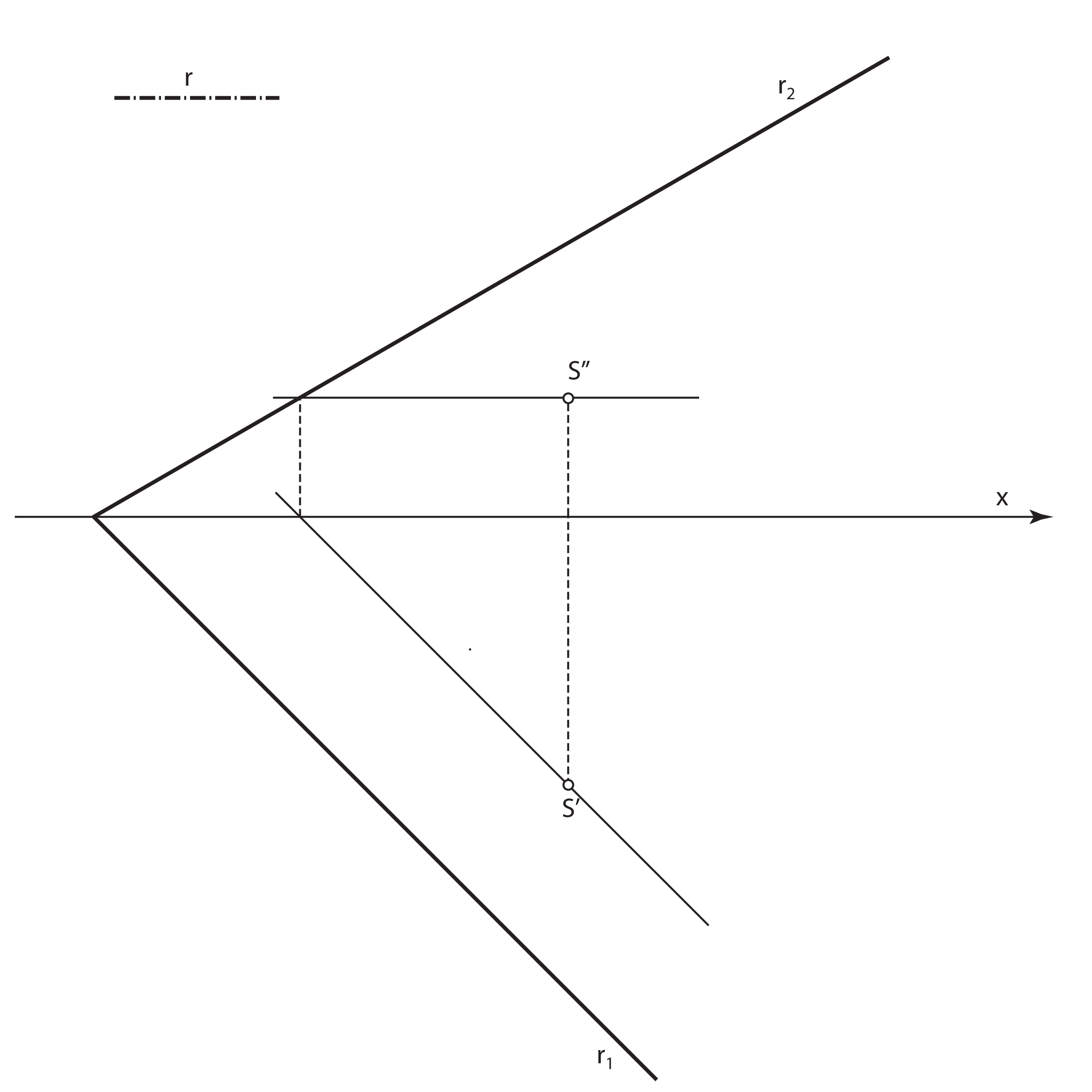
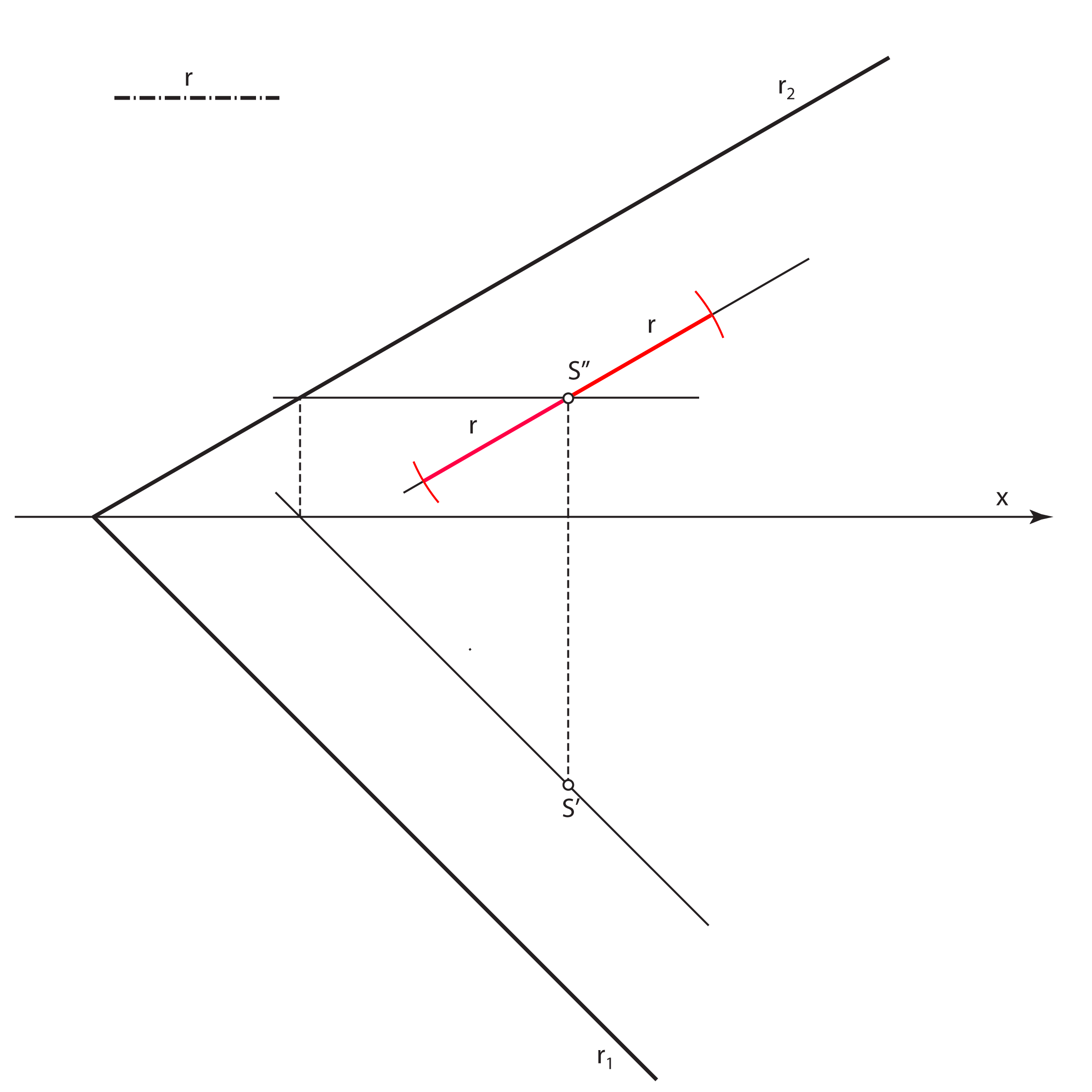
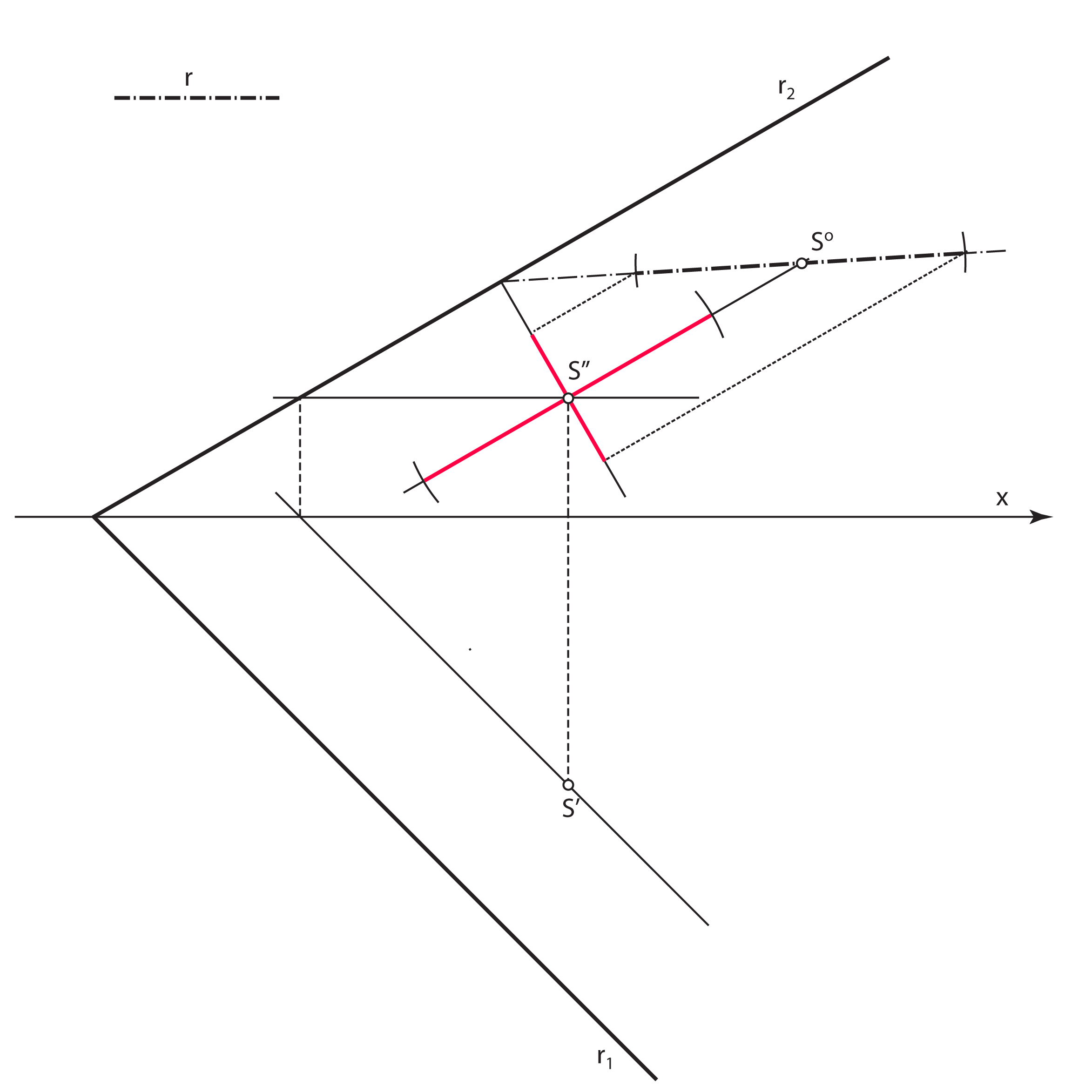
- Promjeri kružnice \(\small k\), koji se u tlocrtu projiciraju u veliku i malu os elipse \(\small k'\) (\(\small \overline{AB}\) i \(\small \overline{CD}\)), u nacrtu se projiciraju u par konjugiranih promjera elipse \(\small k''\)
- Promjeri kružnice \(\small k\), koji se u nacrtu projiciraju u veliku i malu os elipse \(\small k''\) (\(\small \overline{EF}\) i \(\small \overline{GH}\)), u tlocrtu se projiciraju u par konjugiranih promjera elipse \(\small k'\).
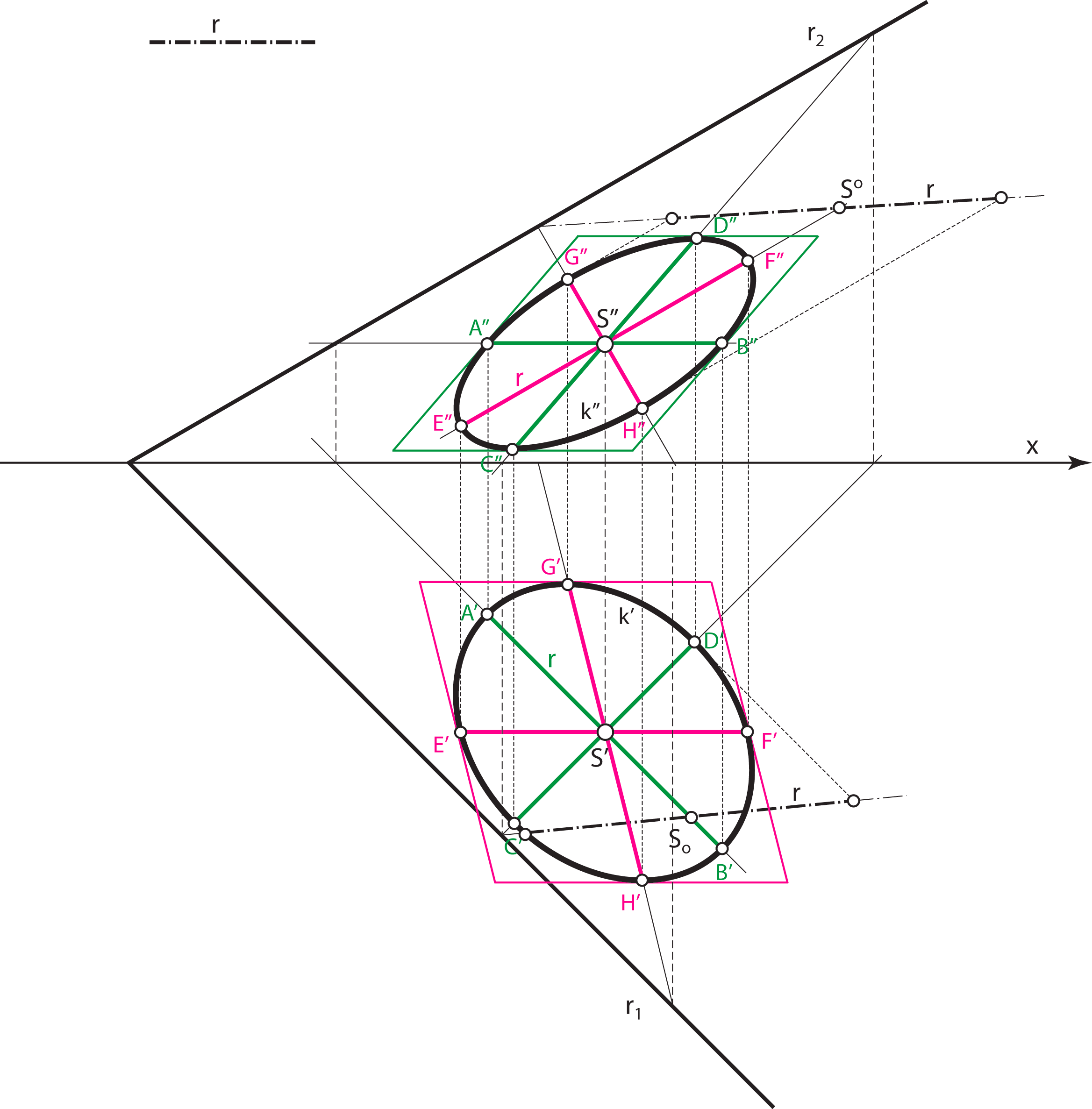
Jasno je da je elipsa \(\small k'\) afina slika rotirane kružnice \(\small (k)\) u ravnini \(\small \Pi_1\), te da je elipsa \(\small k''\) afina slika rotirane kružnice \(\small (k)\) u ravnini \(\small \Pi_2\).
Posebni položaji
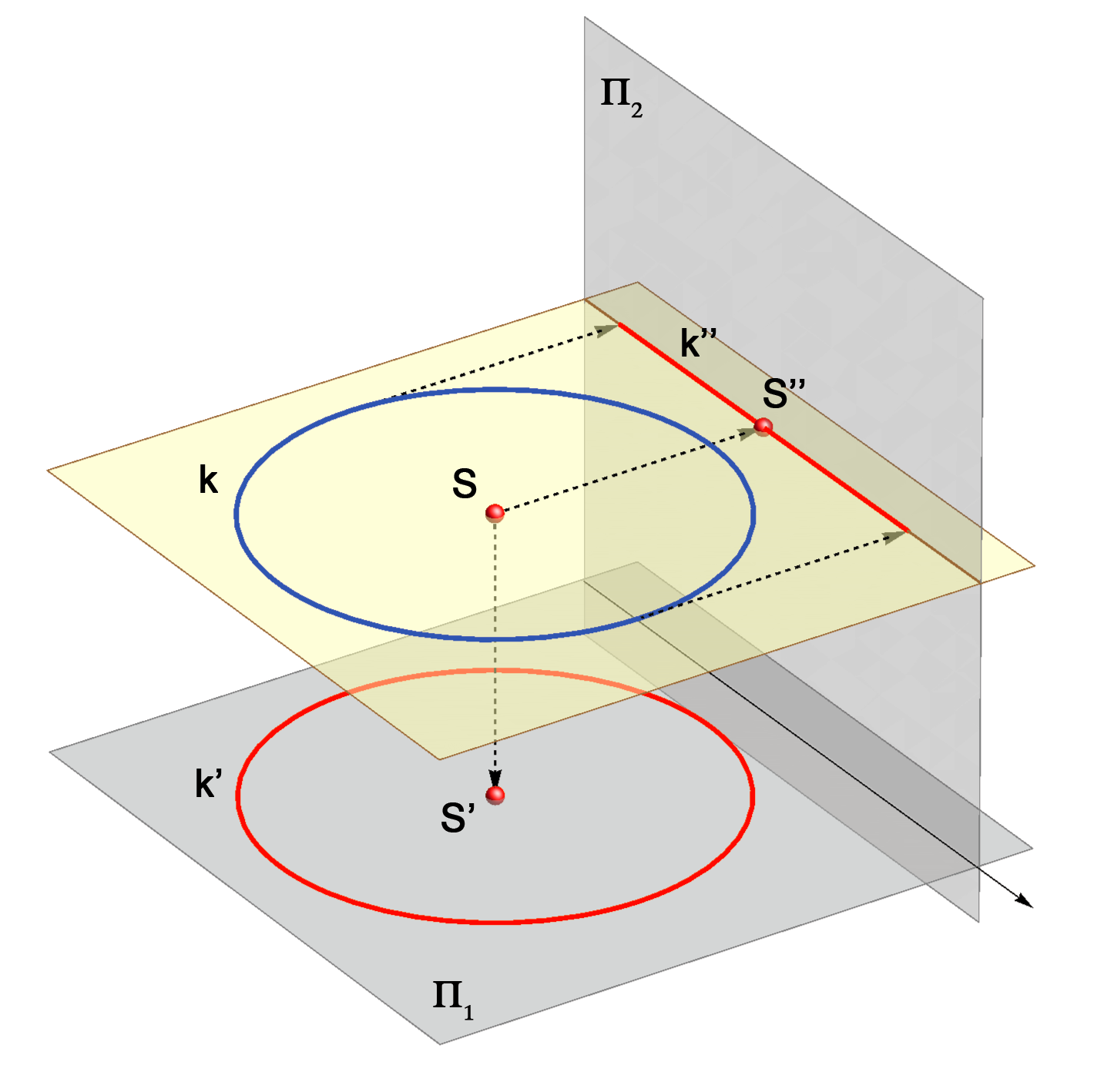
Ako kružnica leži u ravnini koja je okomita na ravninu projekcije (u projicirajućoj ravnini), njezina je projekcija na tu ravninu dužina čija je duljina jednaka promjeru kružnice.
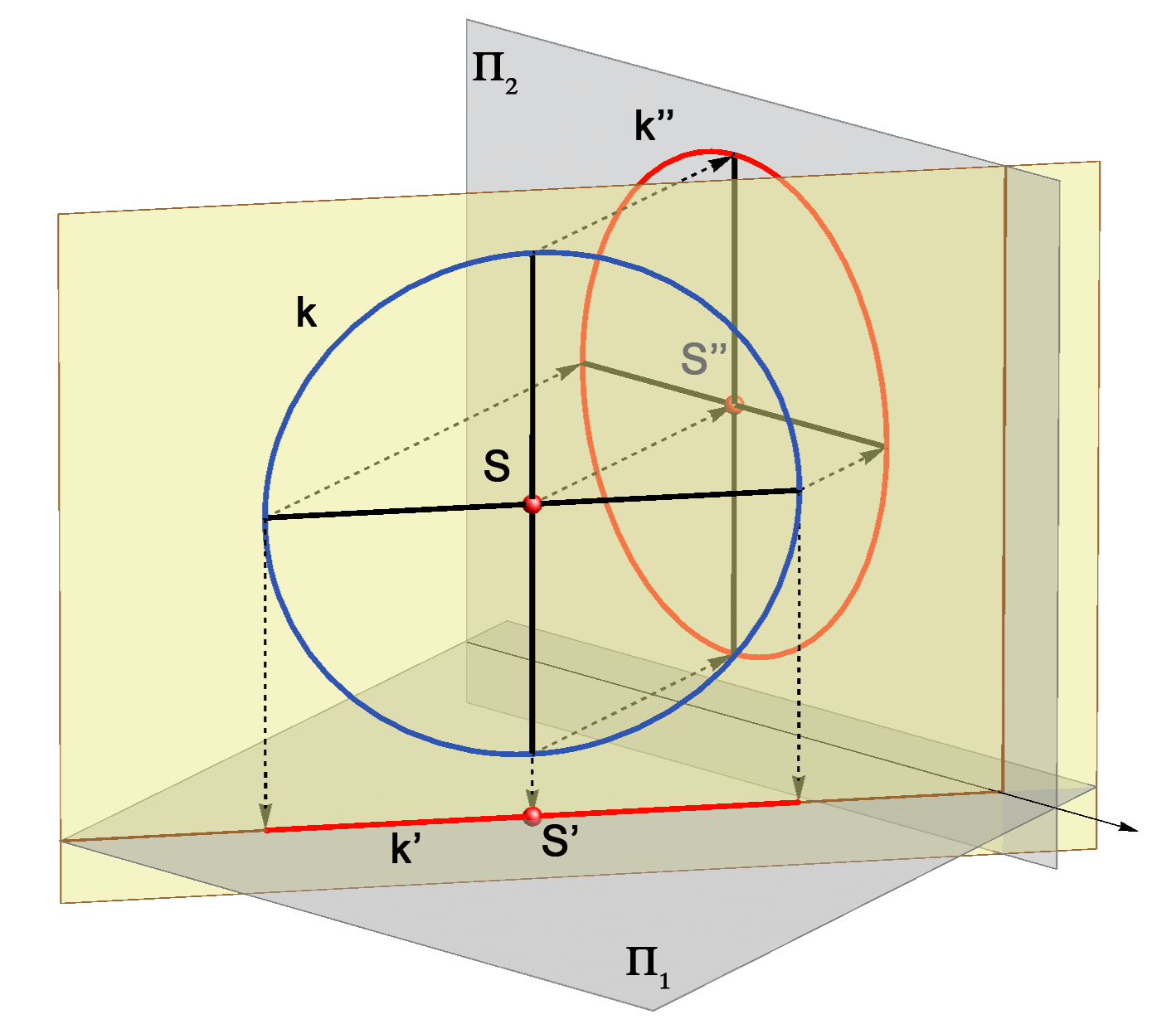
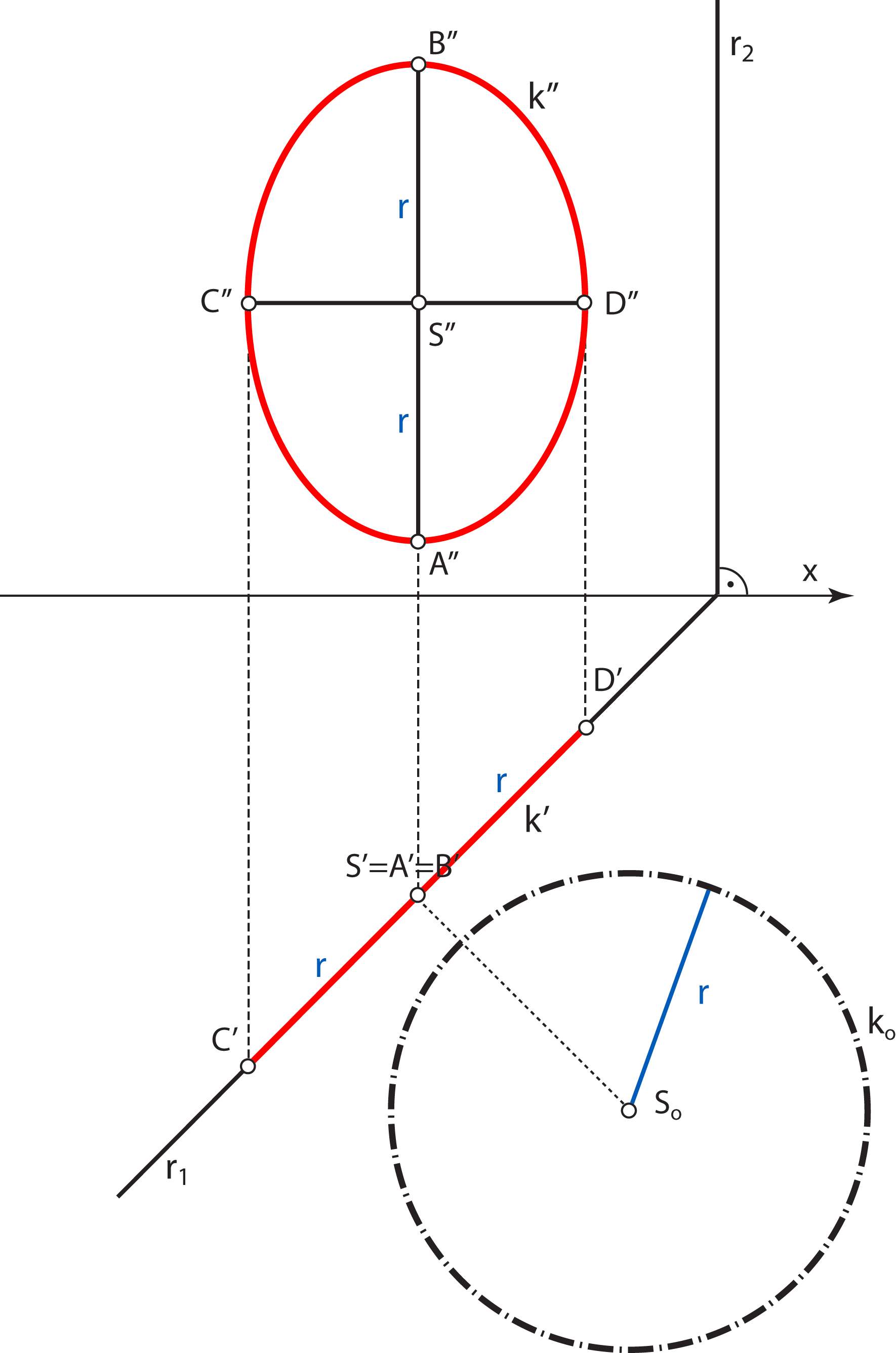
Primjer 1: Projekcije kružnice koja leži u 1. projicirajućoj ravnini.
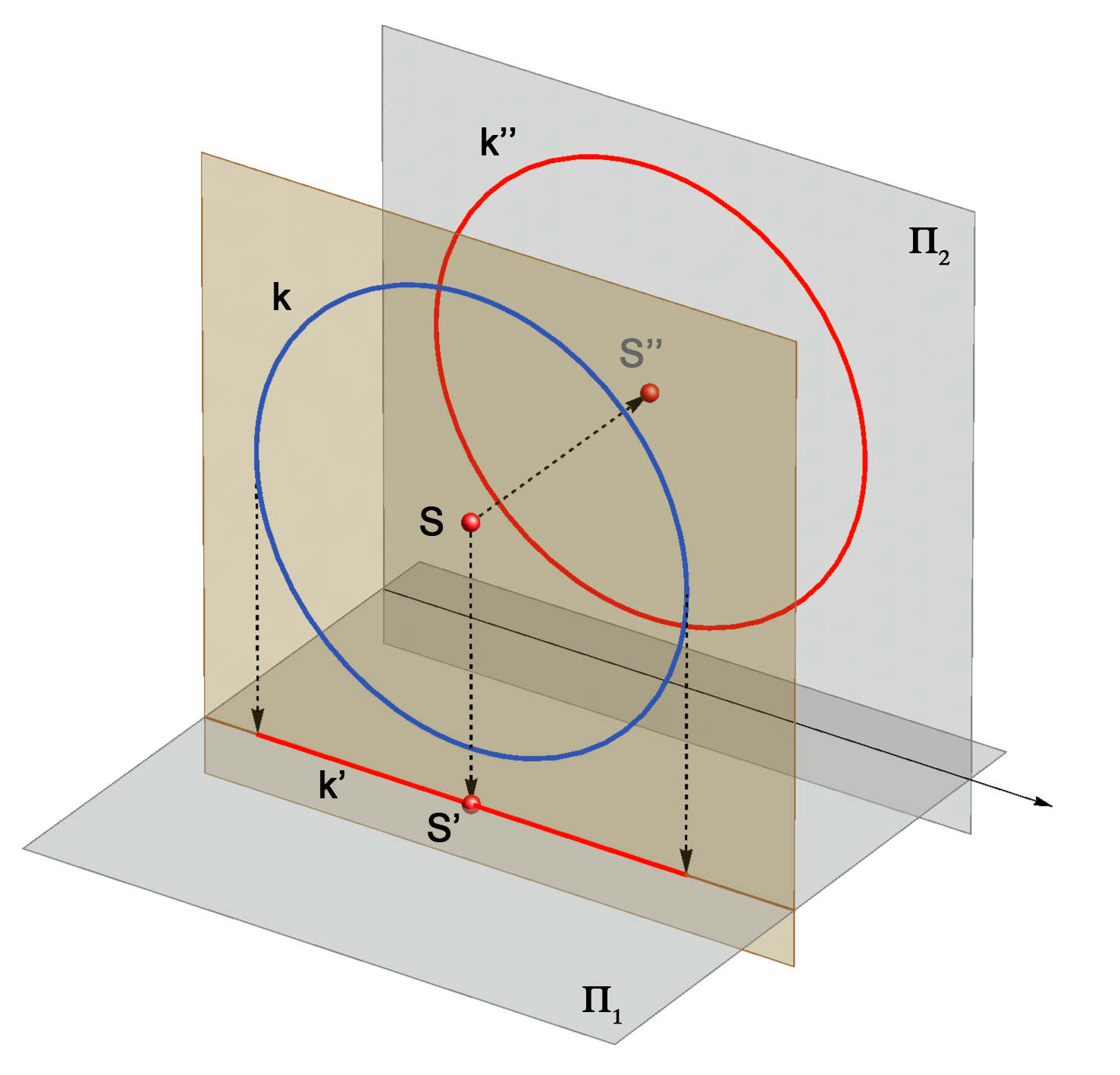
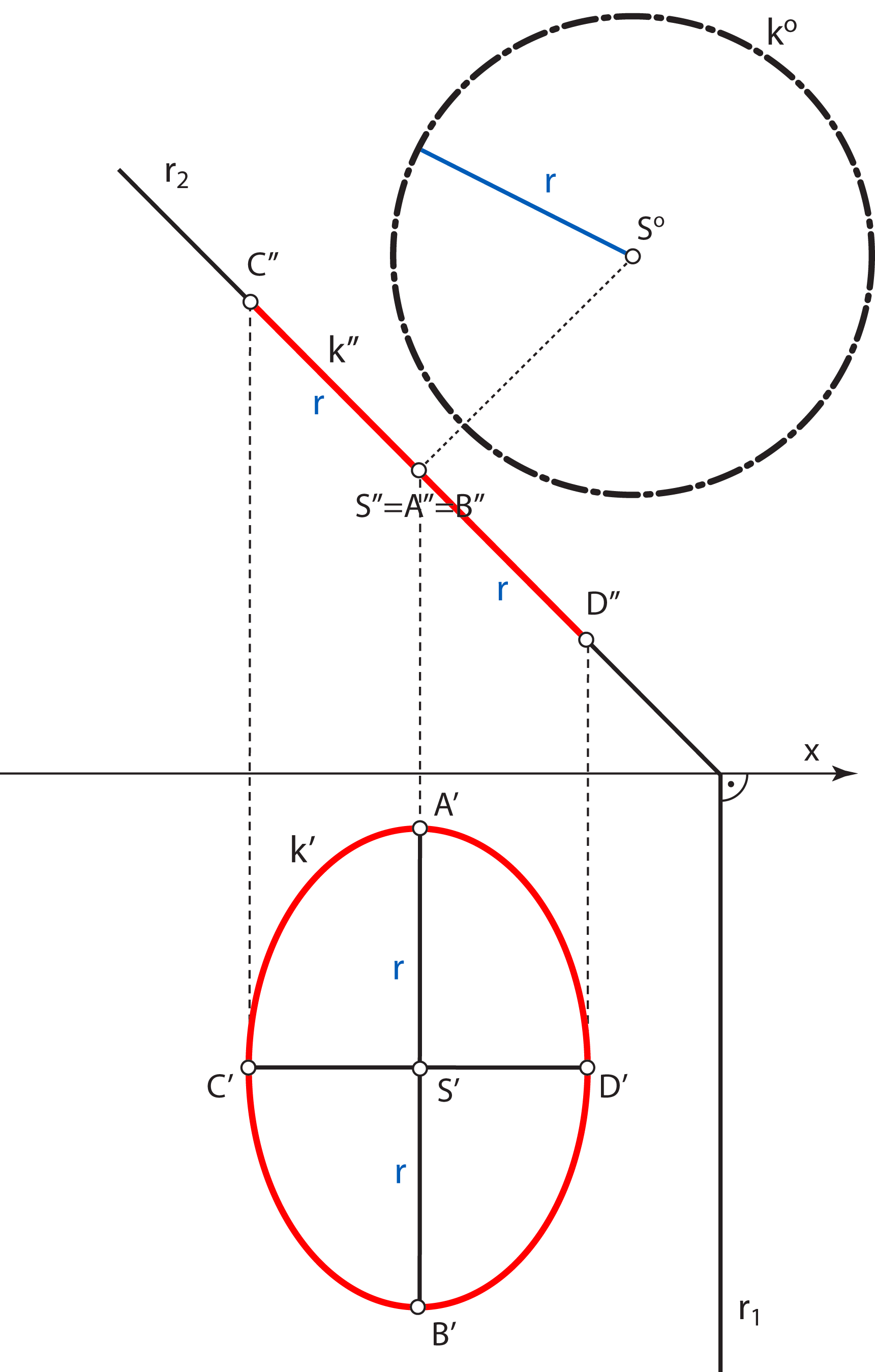
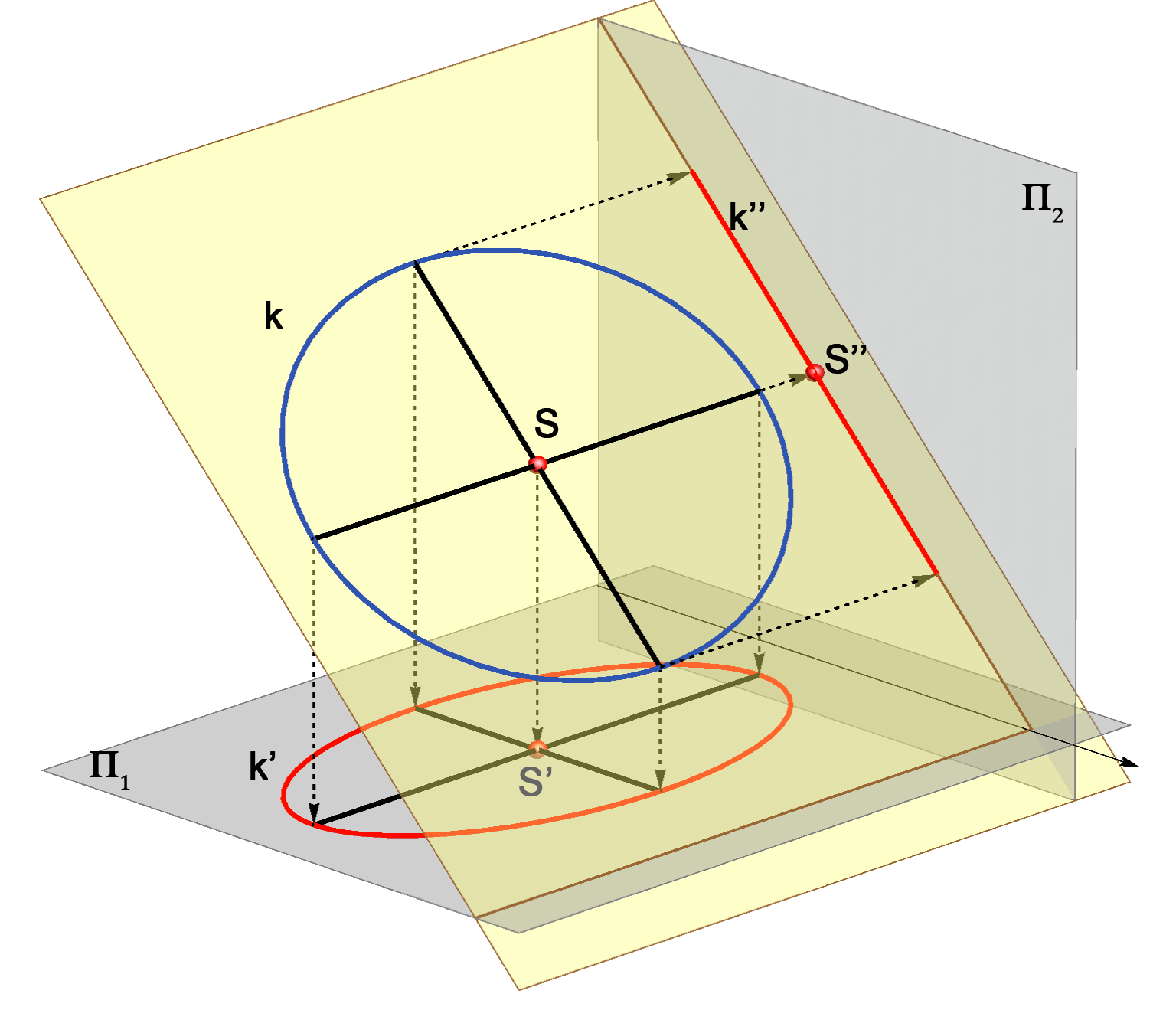
Primjer 2: Projekcije kružnice koja leži u 2. projicirajućoj ravnini.
Ako kružnica leži u ravnini koja je paralelna s jednom od ravnina projekcije, njezina je projekcija na tu ravninu kružnica.