U sljedećim zadacima geometrijsko tijelo, koje je u općem položaju prema ravninama projekcije, treba prikazati u tlocrtu, nacrtu i bokocrtu. Tijelo je zadano nekim svojim odredbenim elementima (primjerice: položaj ravnine osnovke, položaj pojedinih vrhova ili bridova, duljina visine, duljina izvodnice,...). Na temelju poznavanja osnovnih odnosa kod geometrijskih tijela treba razraditi postupak kojim ćemo odrediti i sve ostale bitne elementa tijela, a zatim, primijenom postupaka Mongeove metode, konstruirati tri tražene projekcije zadanog tijela.
Gotovo svi zadaci imaju više od jednog rješenja (ali uvijek konačan broj), a prikazati treba samo jedno od njih.
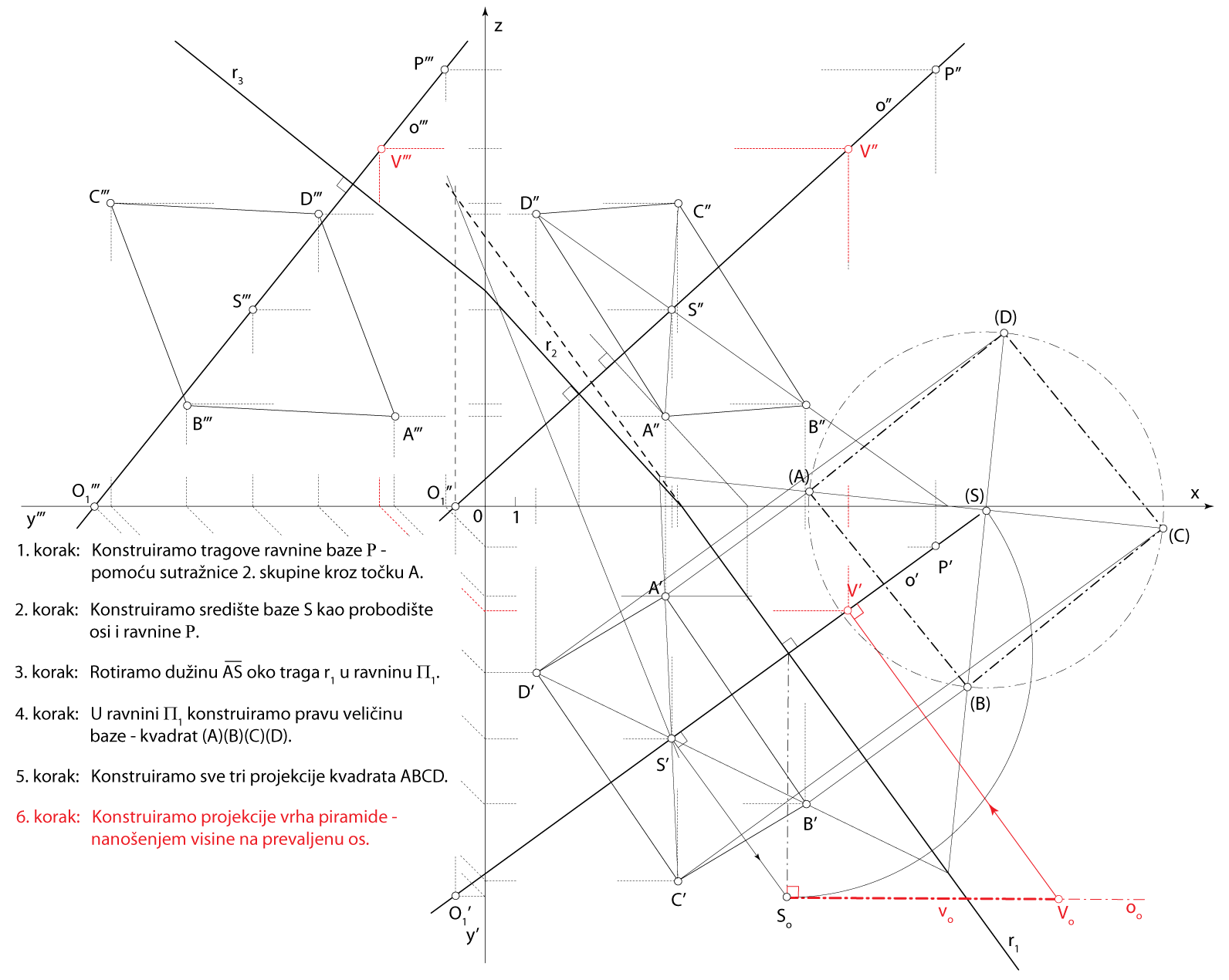
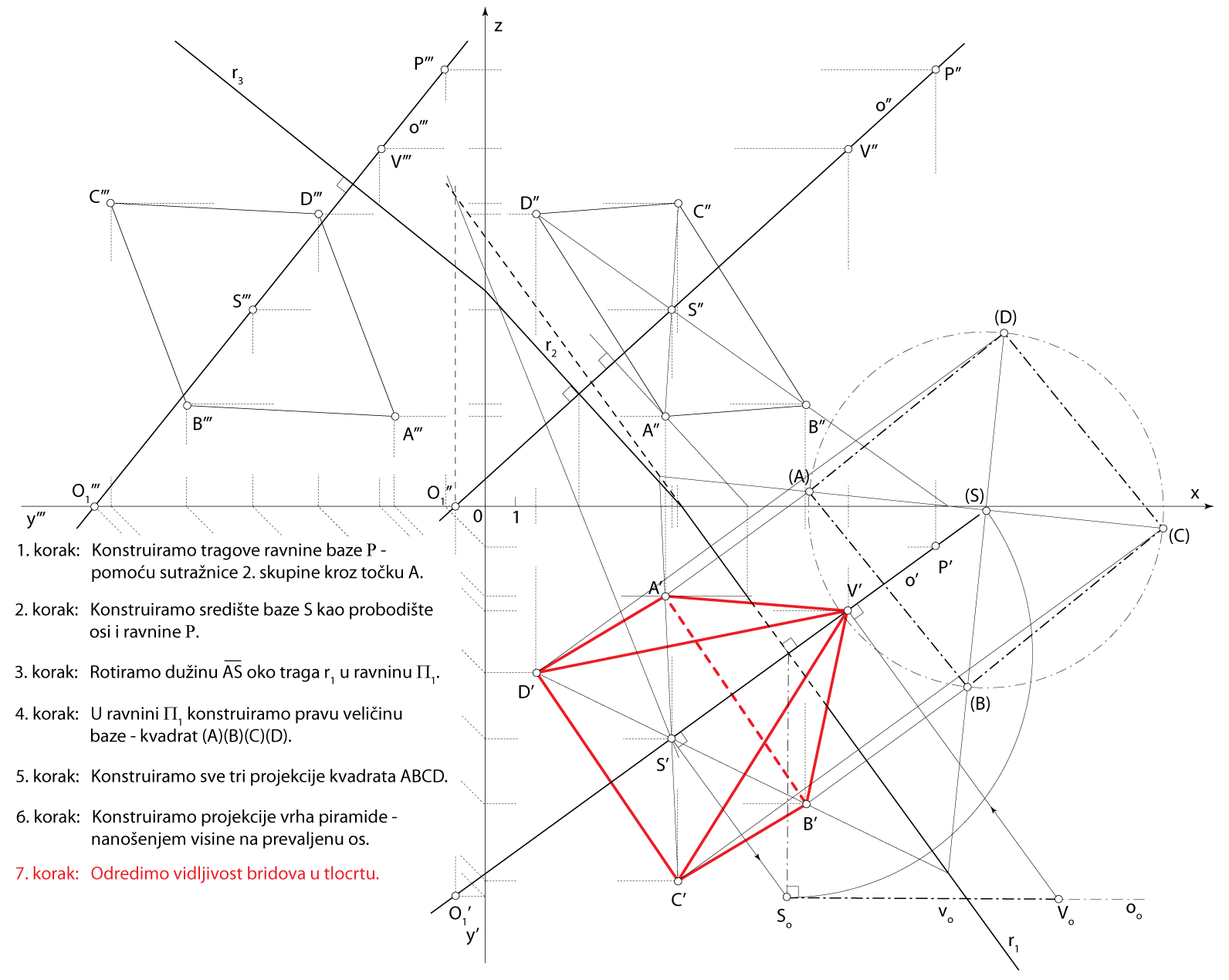
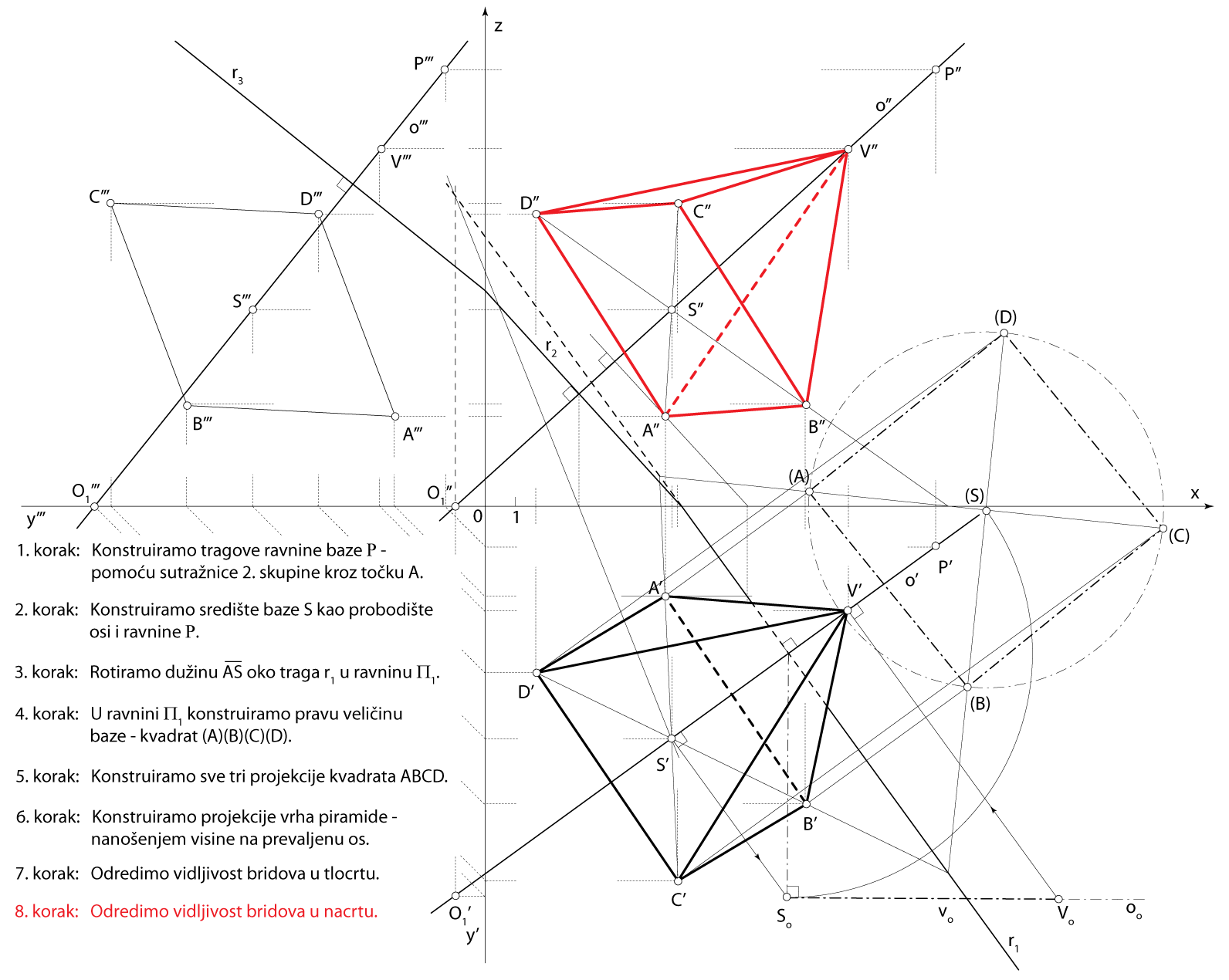
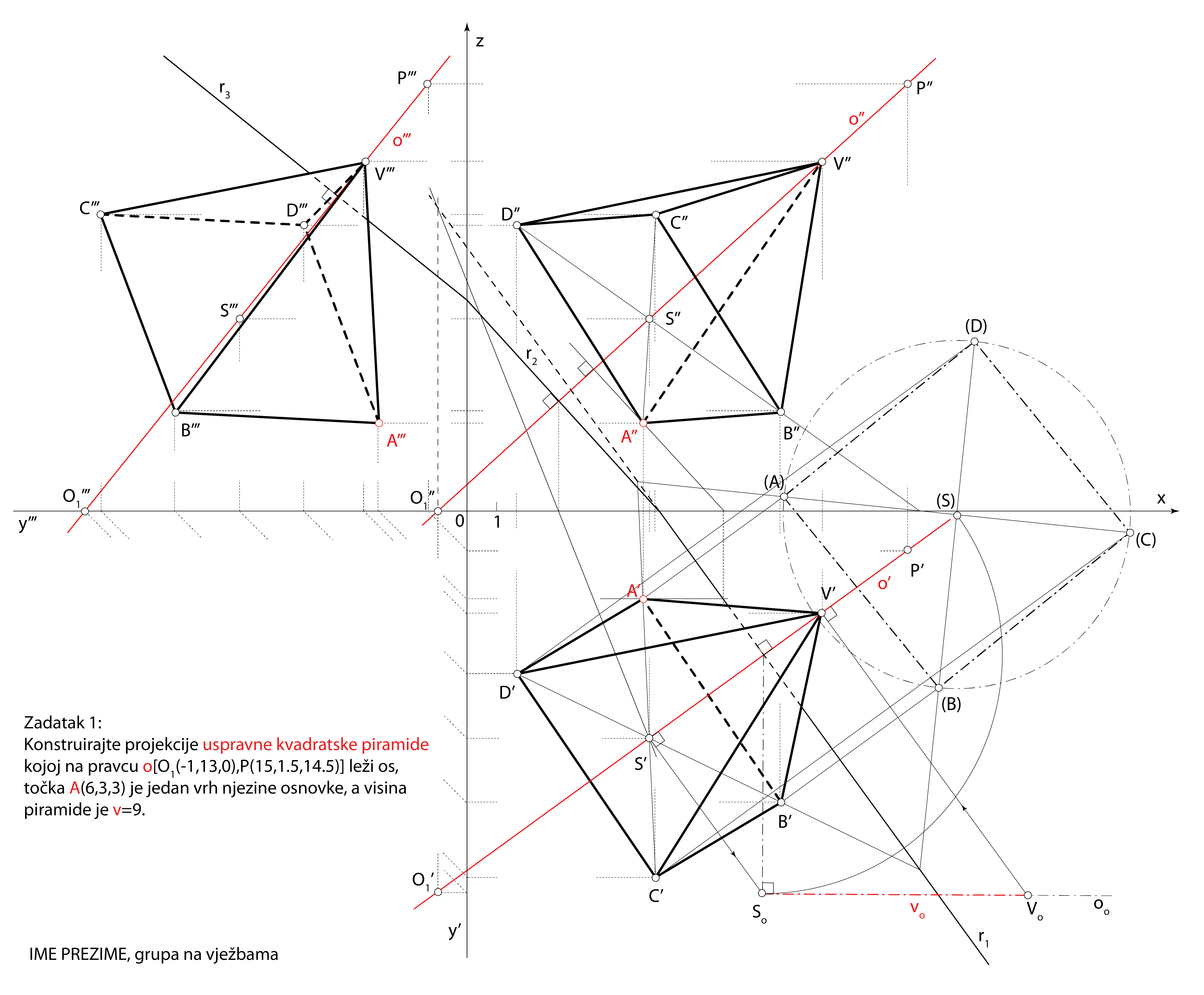
Zadatak 1: Konstruirajte projekcije uspravne kvadratske piramide kojoj na pravcu \(\small o[O_1(-1,13,0), P(15,1.5,14.5)]\) leži os, točka \(\small A(6,3,3)\) jedan je vrh njezine osnovke, a visina je piramide \(\small v=9\).
Shema prostornog rješenja
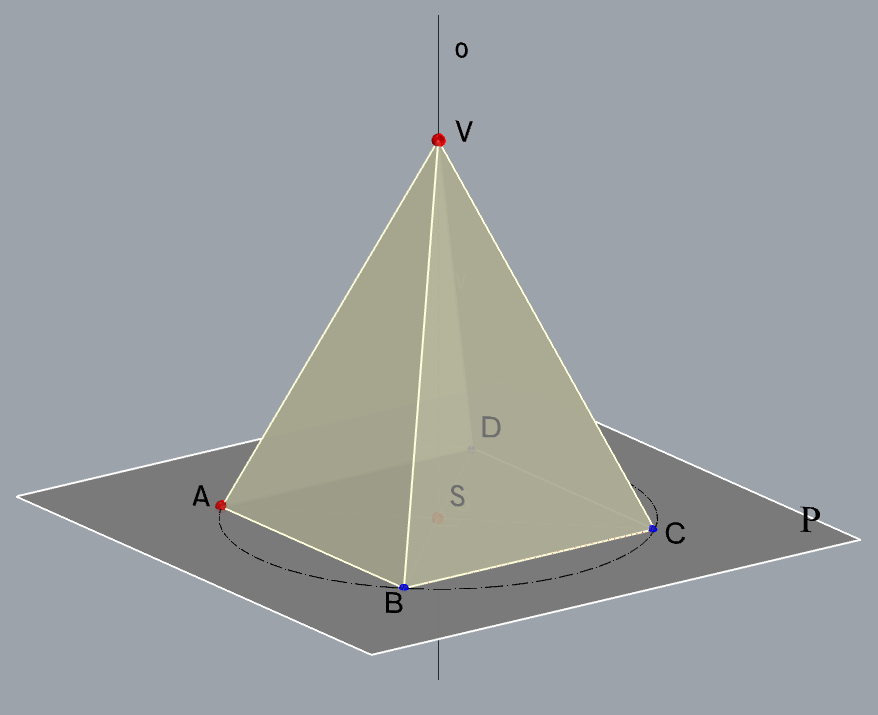
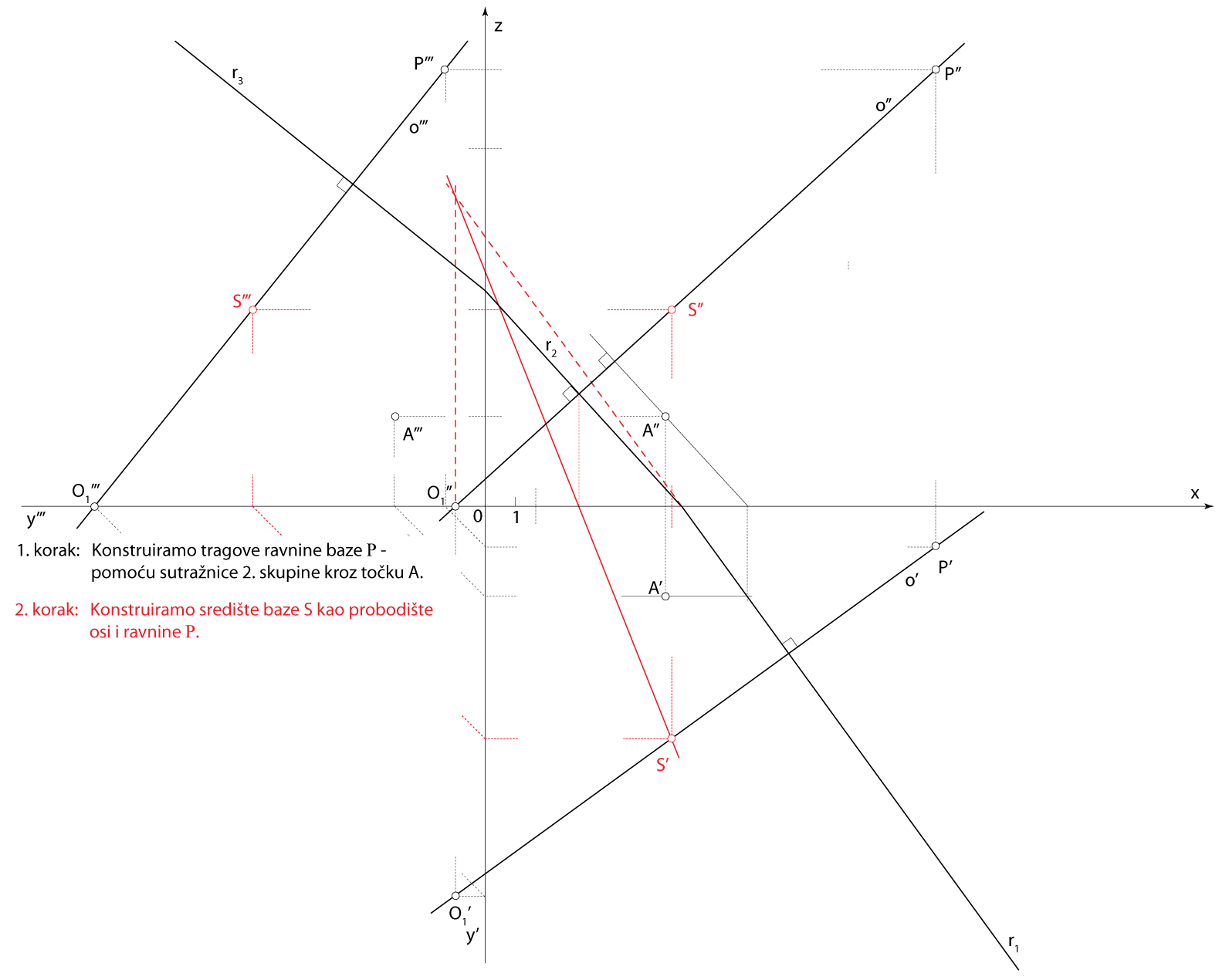
- \(\small \mathrm P -\) ravnina baze
\(\small A\in\,\)\(\small\mathrm P\), \(\small o \perp \) \(\small\mathrm P\) - \(\small S-\) središte baze piramide
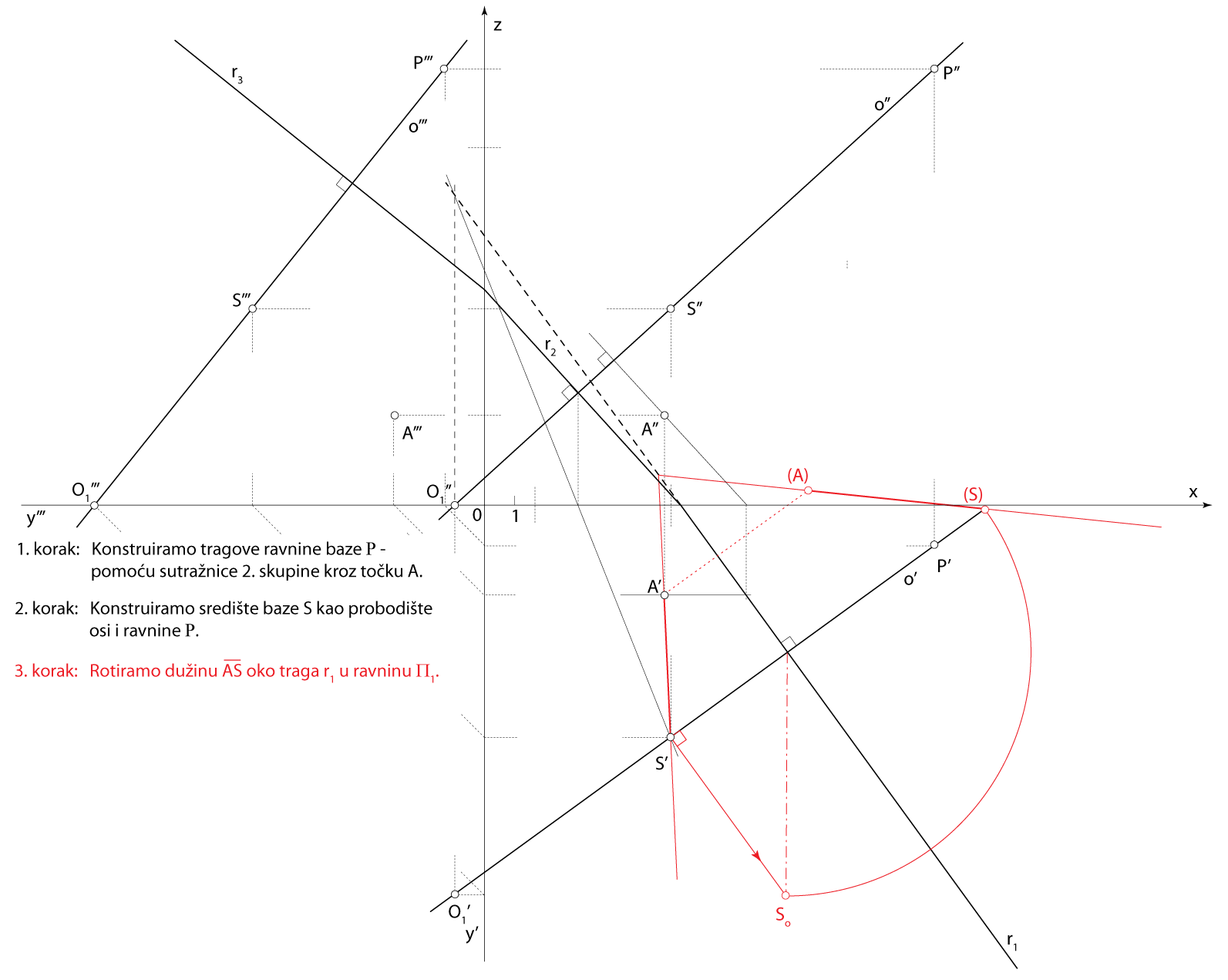
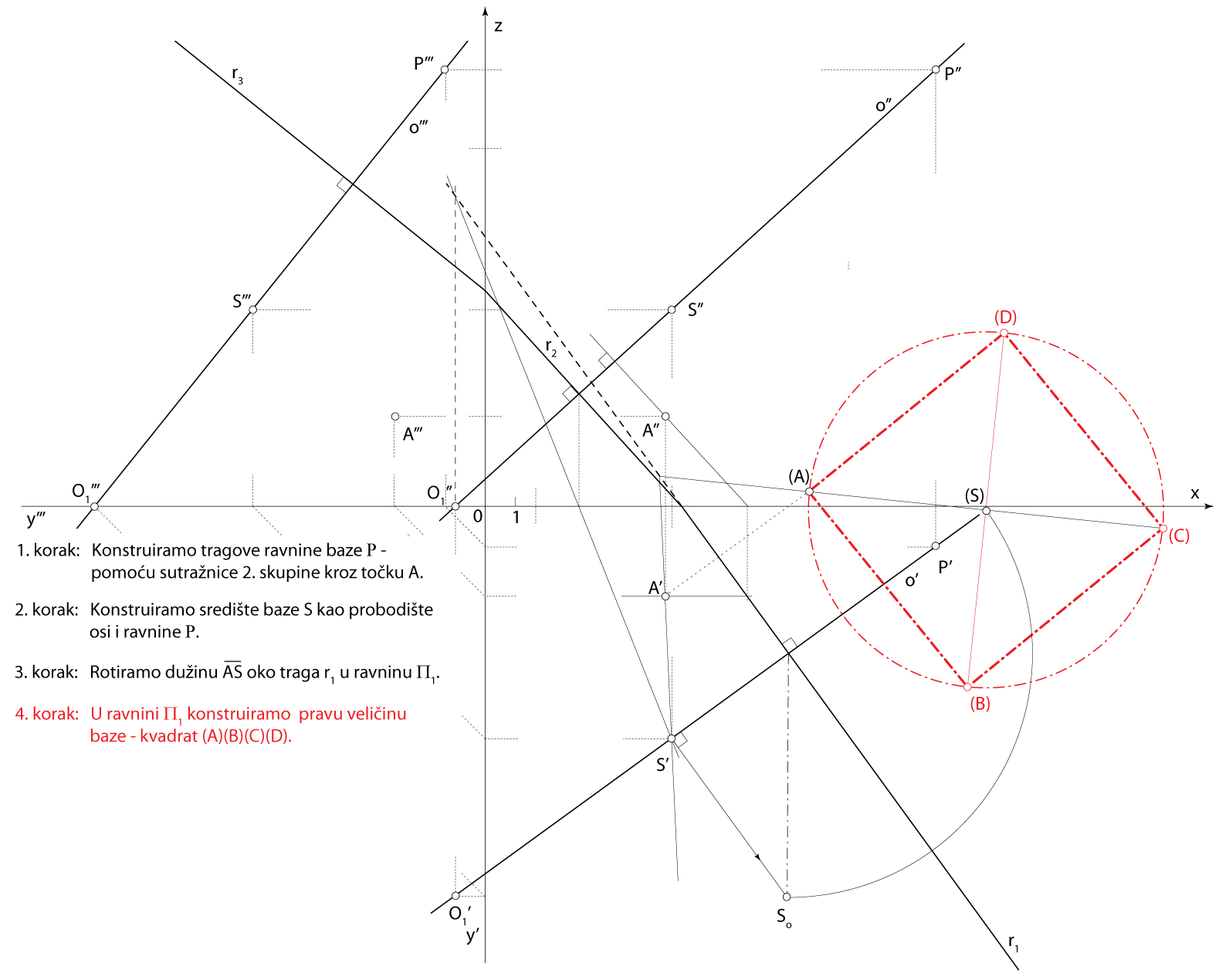
\(\small S=o\,\cap\) \(\small\mathrm P\) - \(\small \Box ABCD\subset\,\,\)\(\small\mathrm P\)
- \(\small V-\) vrh piramide
\(\small V\in o\), \(\small \,\,d(S,V)=v\)
Rješenje u Mongeovoj projekciji (po koracima)
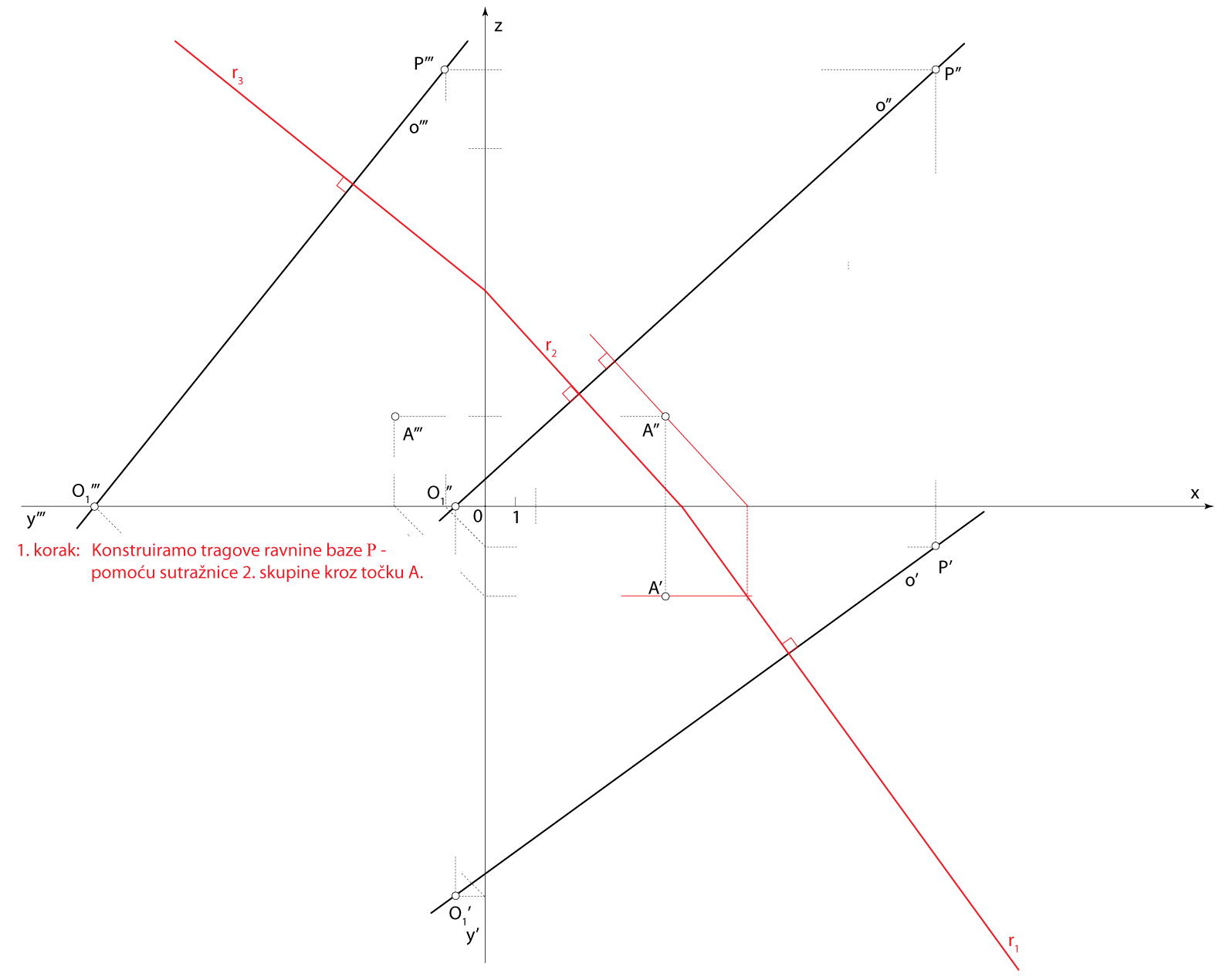
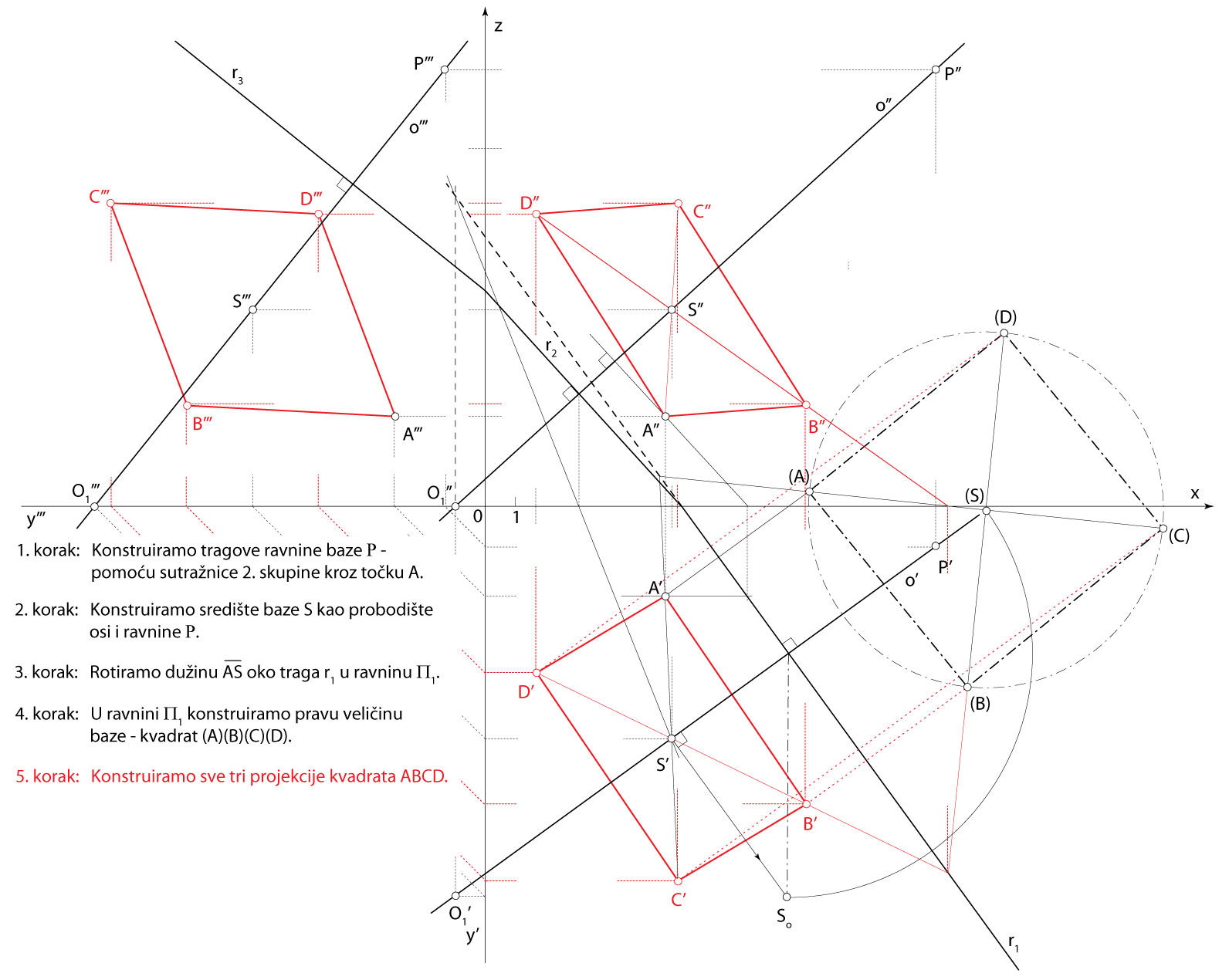
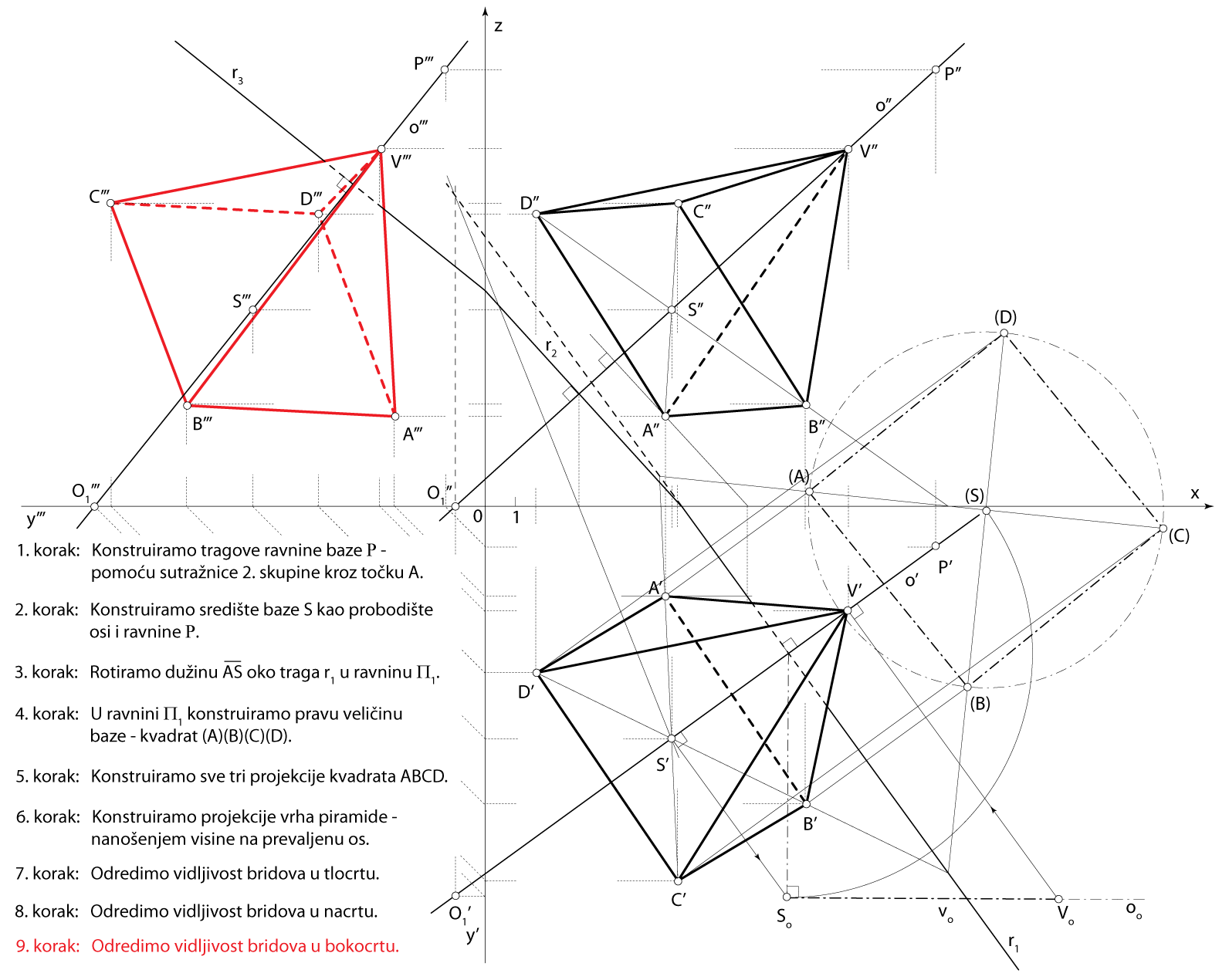
Završni crtež
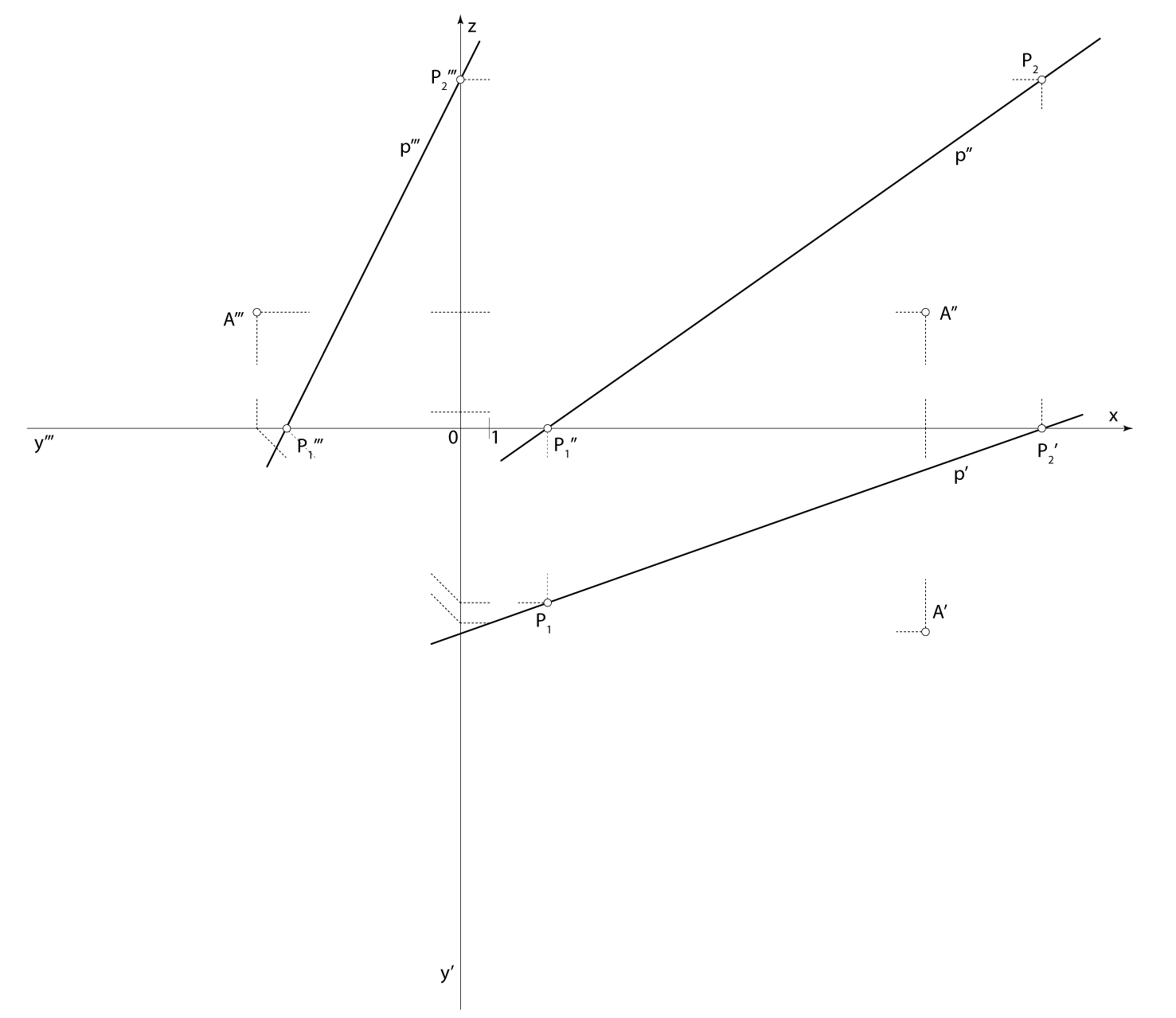
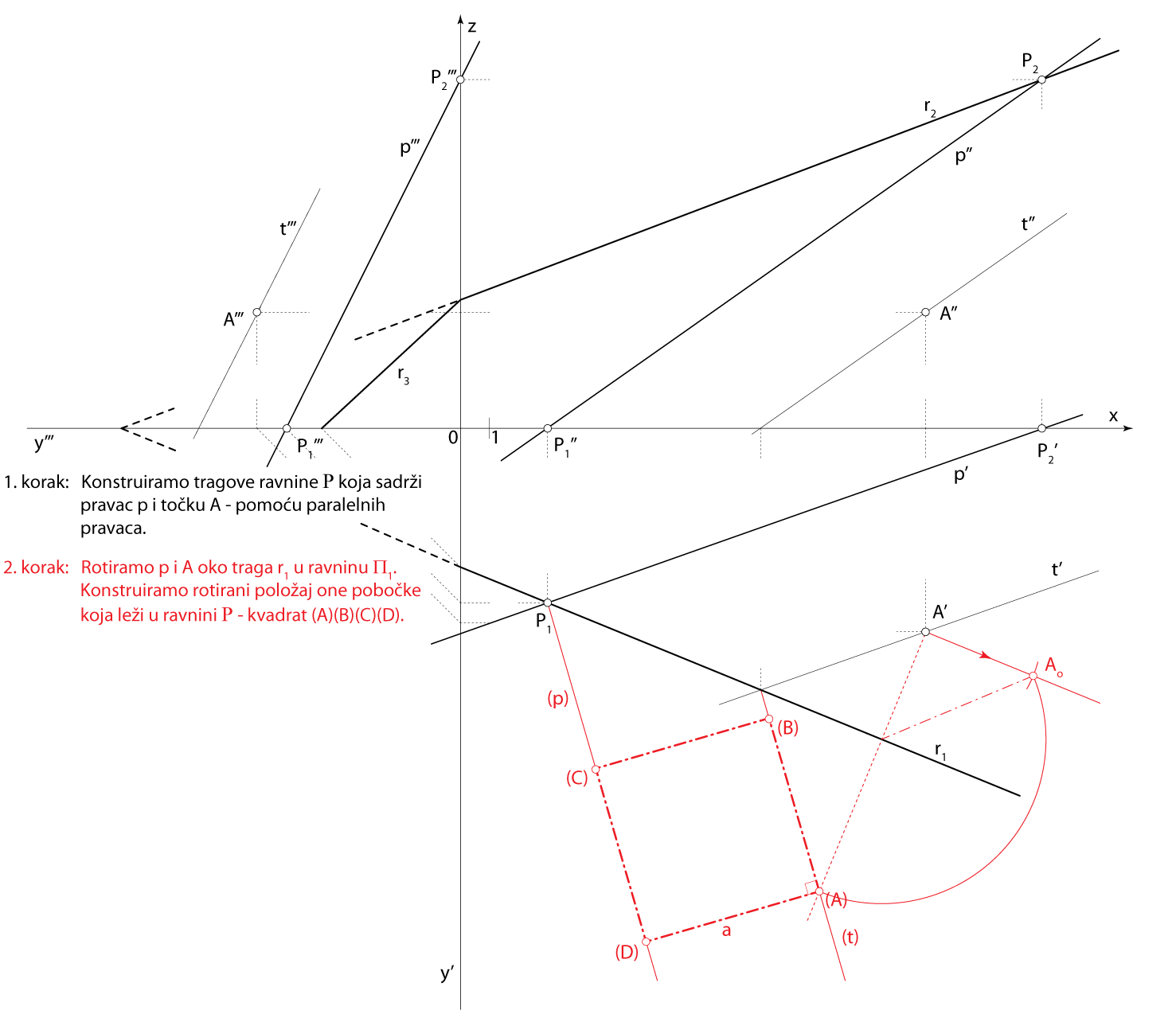
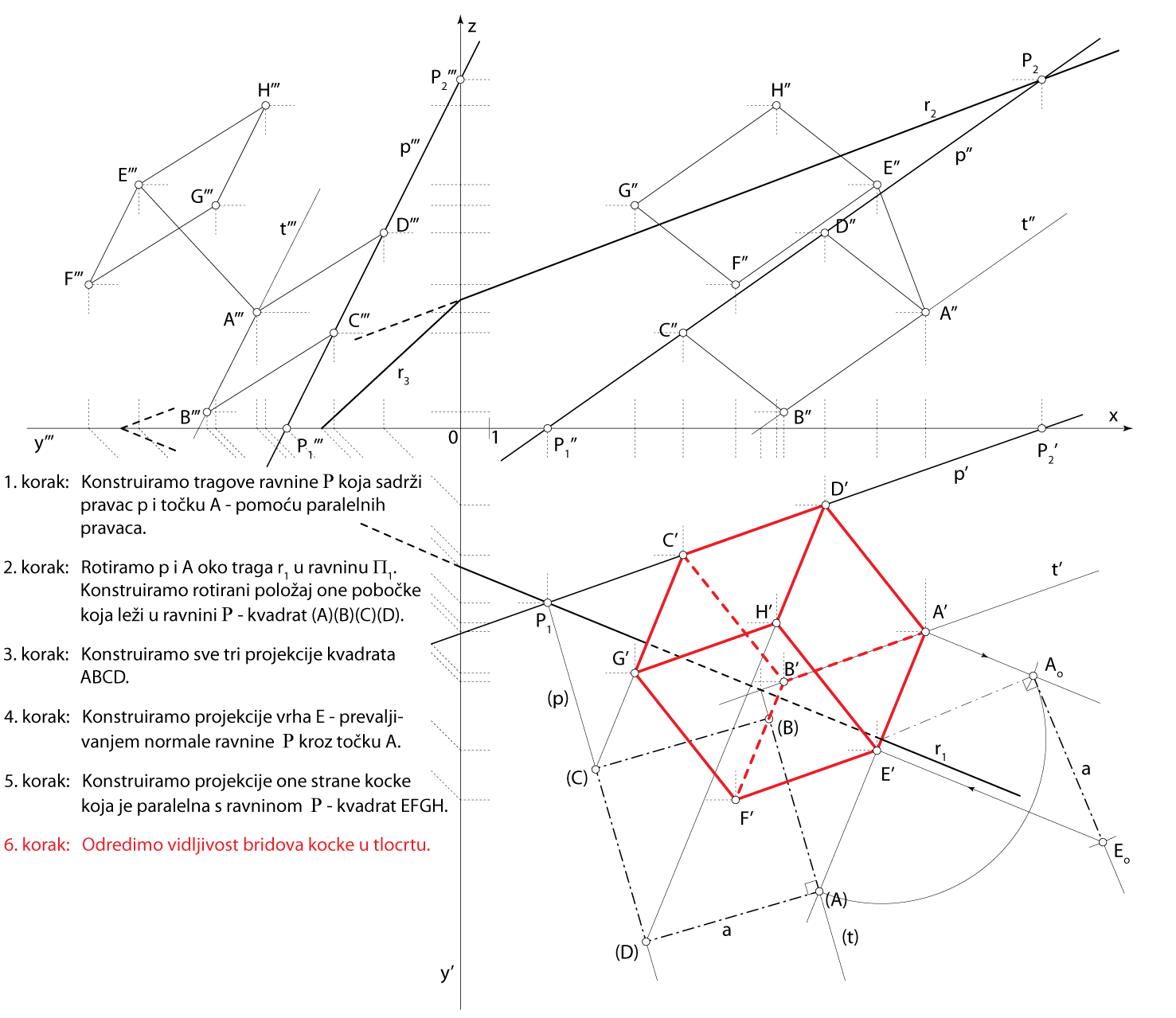
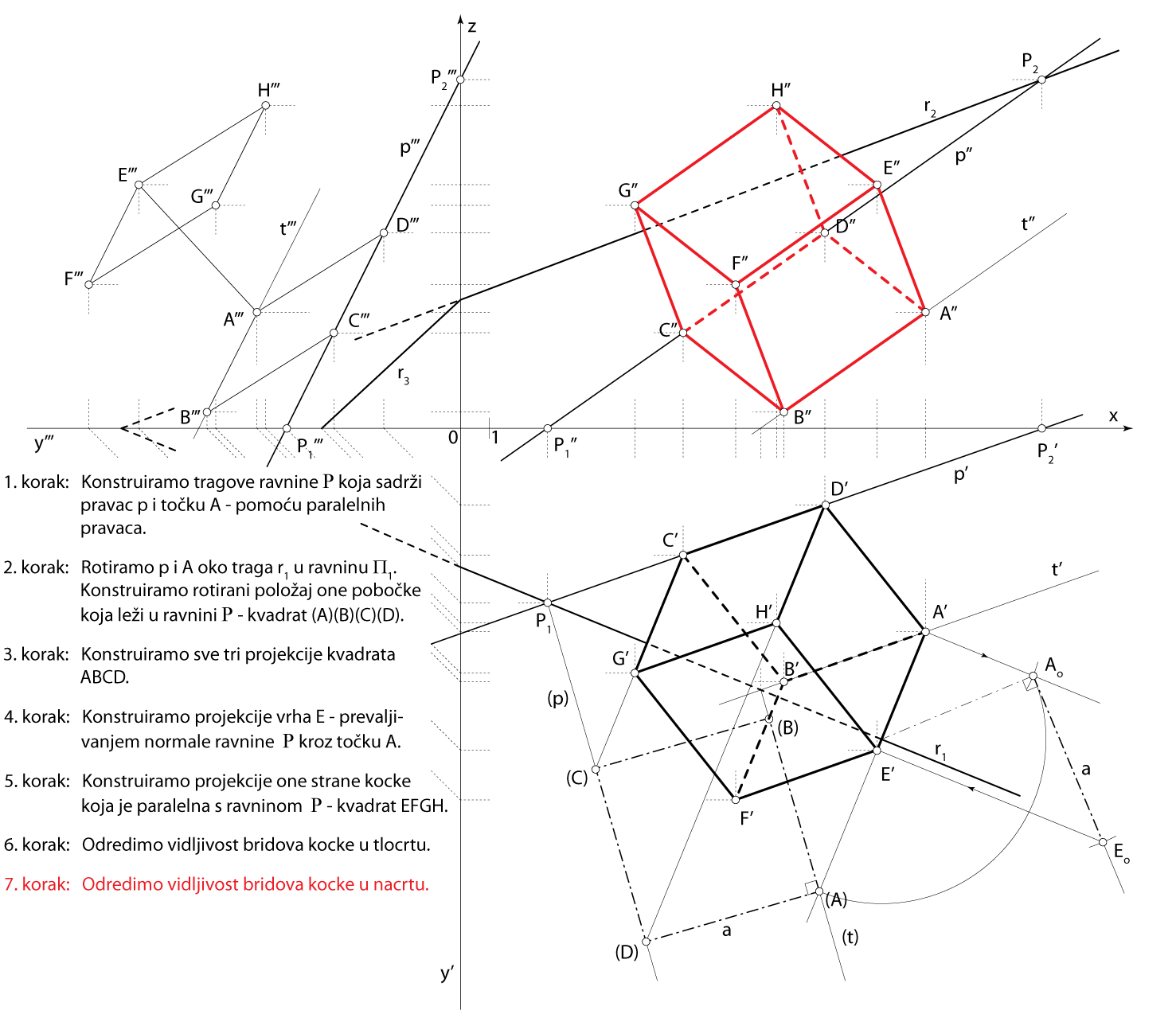
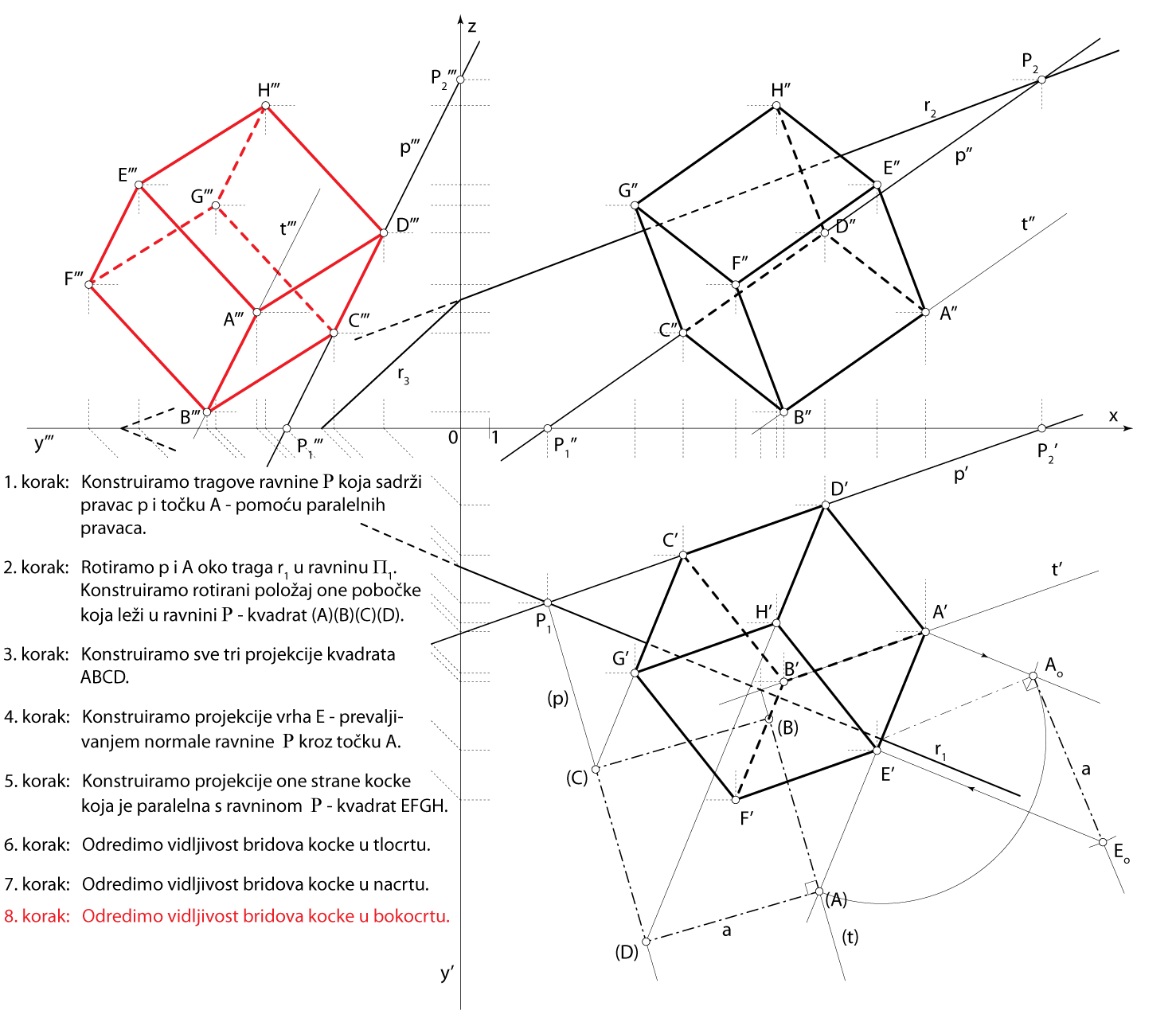
Zadatak 2: Konstruirajte projekcije kocke kojoj na pravcu \(\small p[P_1(3,6,0), P_2(20,0,12)]\) leži jedan brid, a točka \(\small A(16,7,4)\) jedan je vrh njezine pobočke kojoj taj brid pripada.
Shema prostornog rješenja
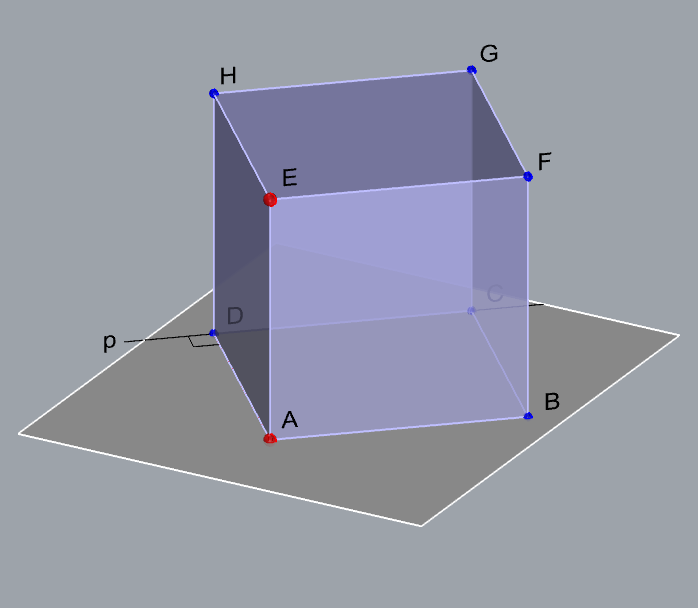
- \(\small\mathrm P\) \(\small -\) ravnina u kojoj leži jedna strana kocke \(\small A\in\) \(\small\mathrm P\), \(\small p \subset \) \(\small\mathrm P\)
- \(\small \overline{AD}-\) jedan brid kocke \(\small D\in p\), \(\small \overline{AD}\perp p\)
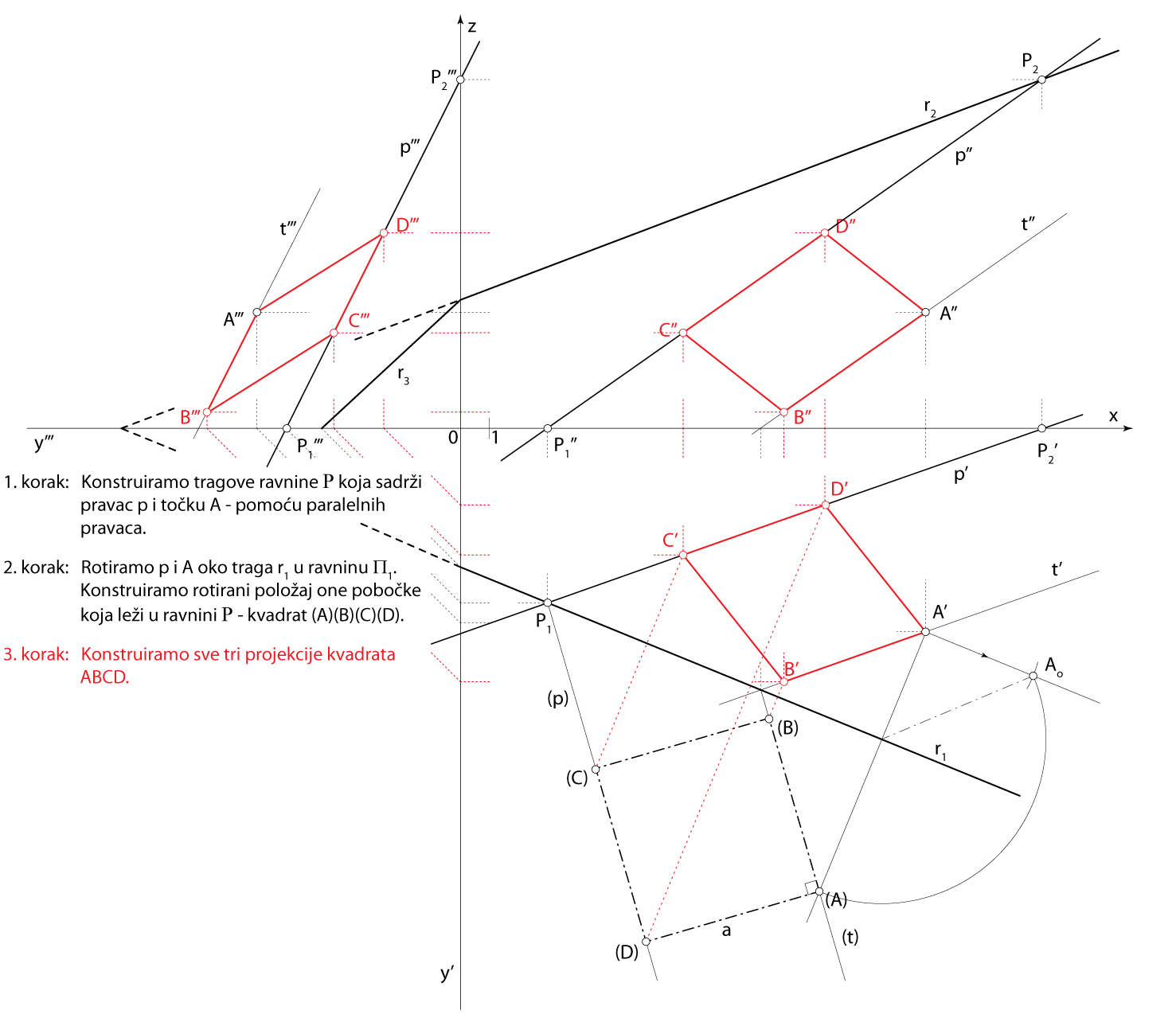
- \(\small \Box ABCD\subset\,\,\)\(\small\mathrm P\)
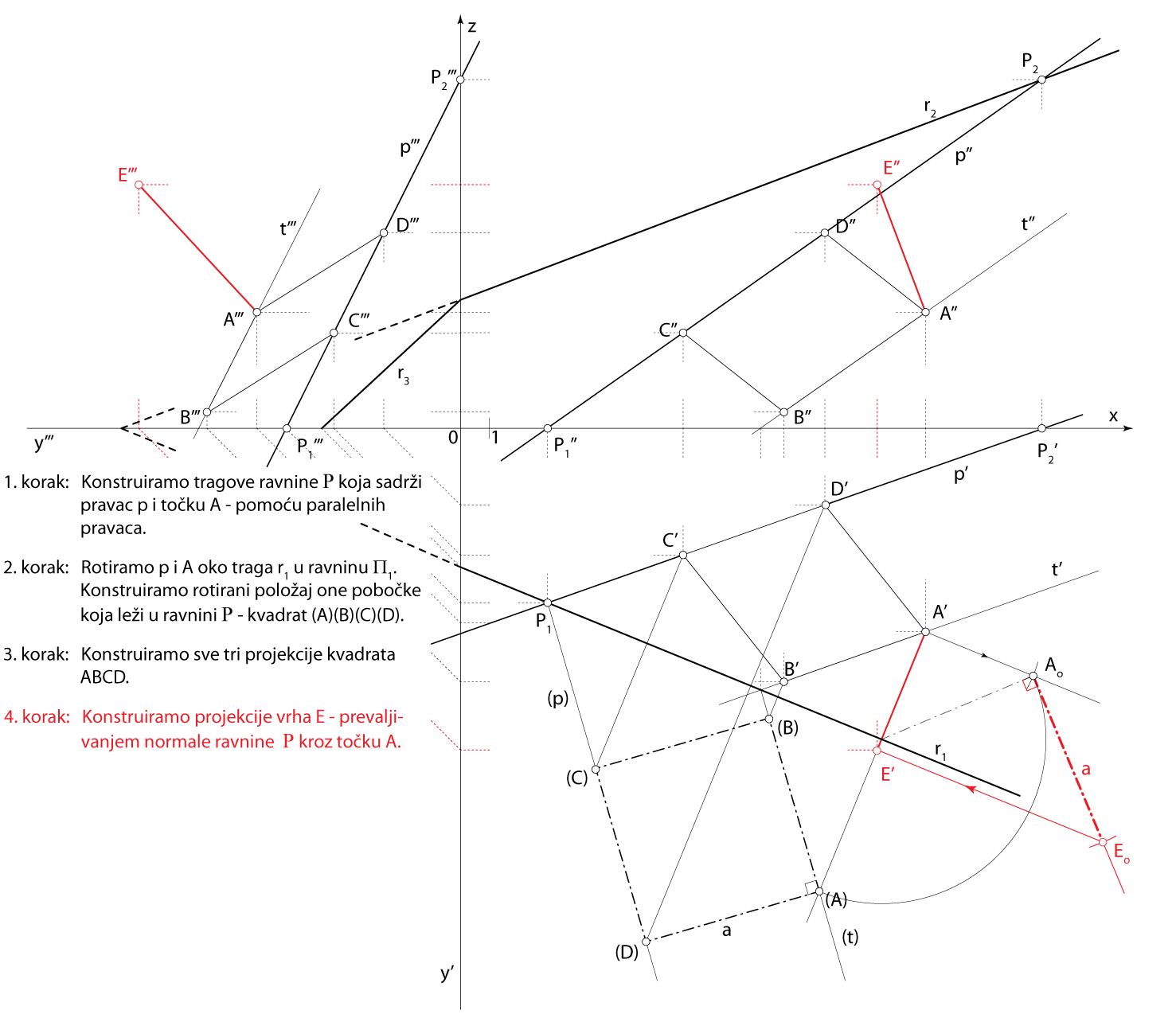
- \(\small E-\) vrh kocke u ravnini paralelnoj s \(\small\mathrm P\) \(\small \overline{AE}\perp\,\,\)\(\small\mathrm P\), \(\small \,\,d(A,E)=d(A,D)\)
- \(\small \Box EFGH\) u ravnini paralelnoj s \(\small\mathrm P\)
Rješenje u Mongeovoj projekciji (po koracima)
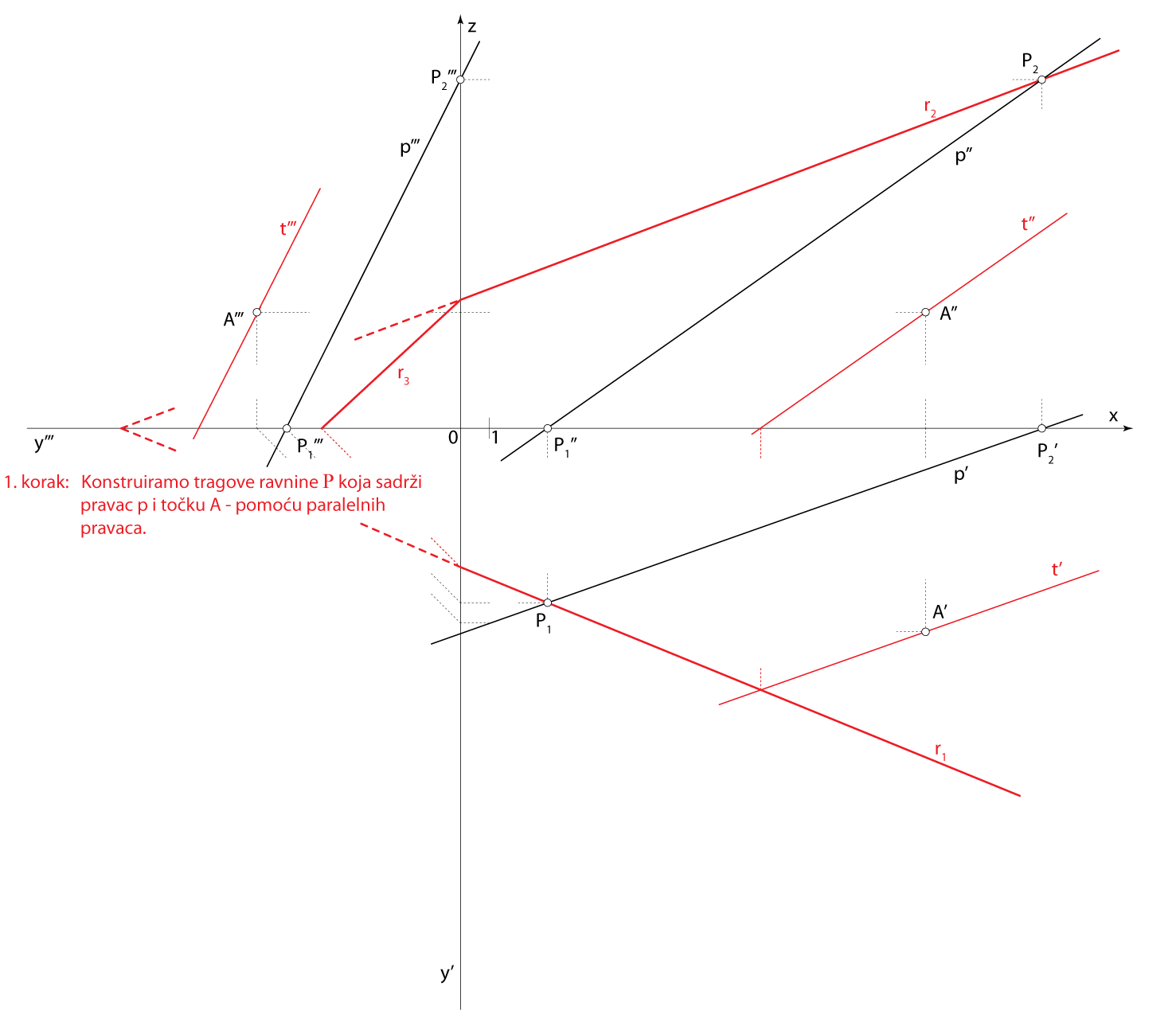
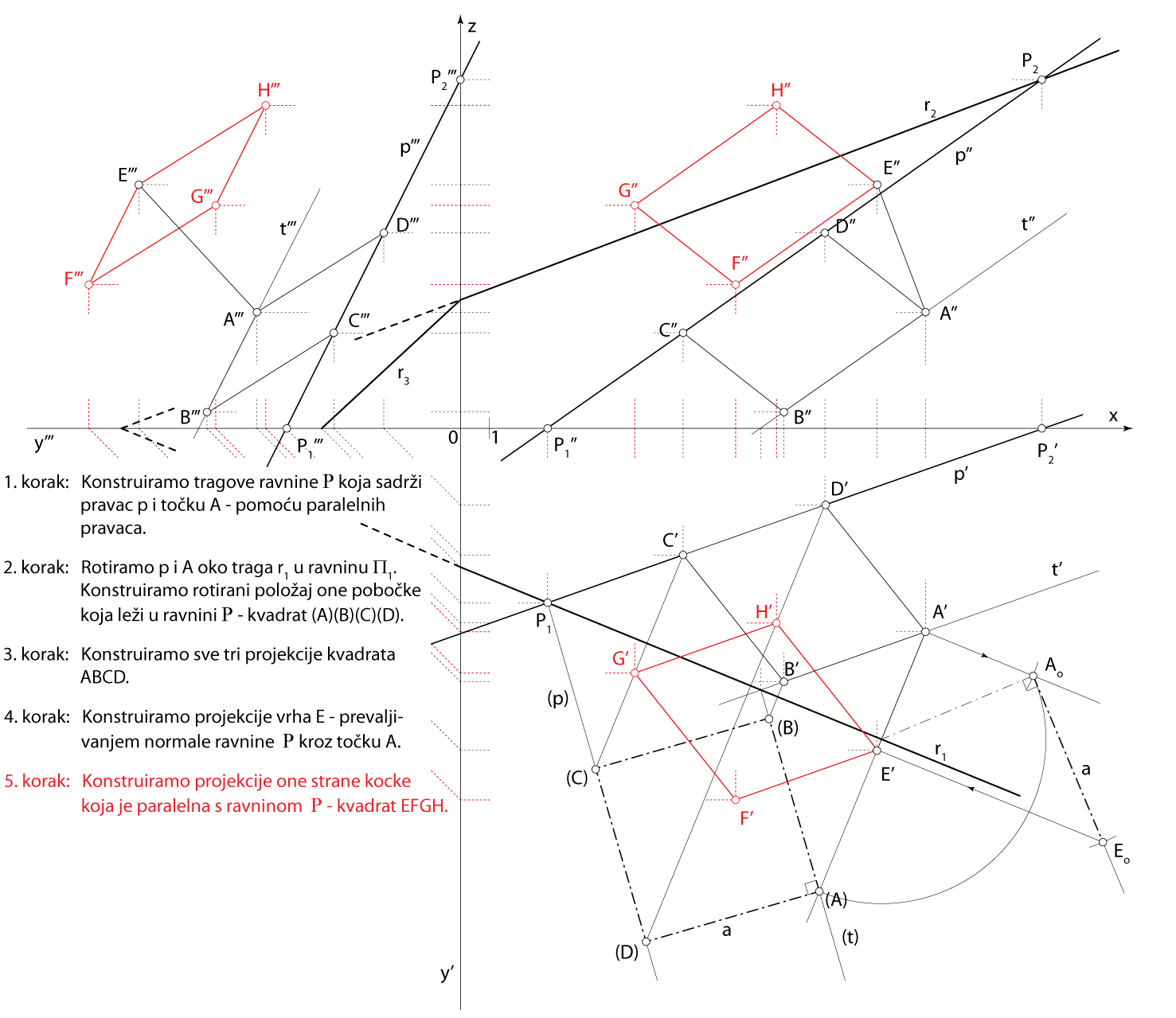
Završni crtež
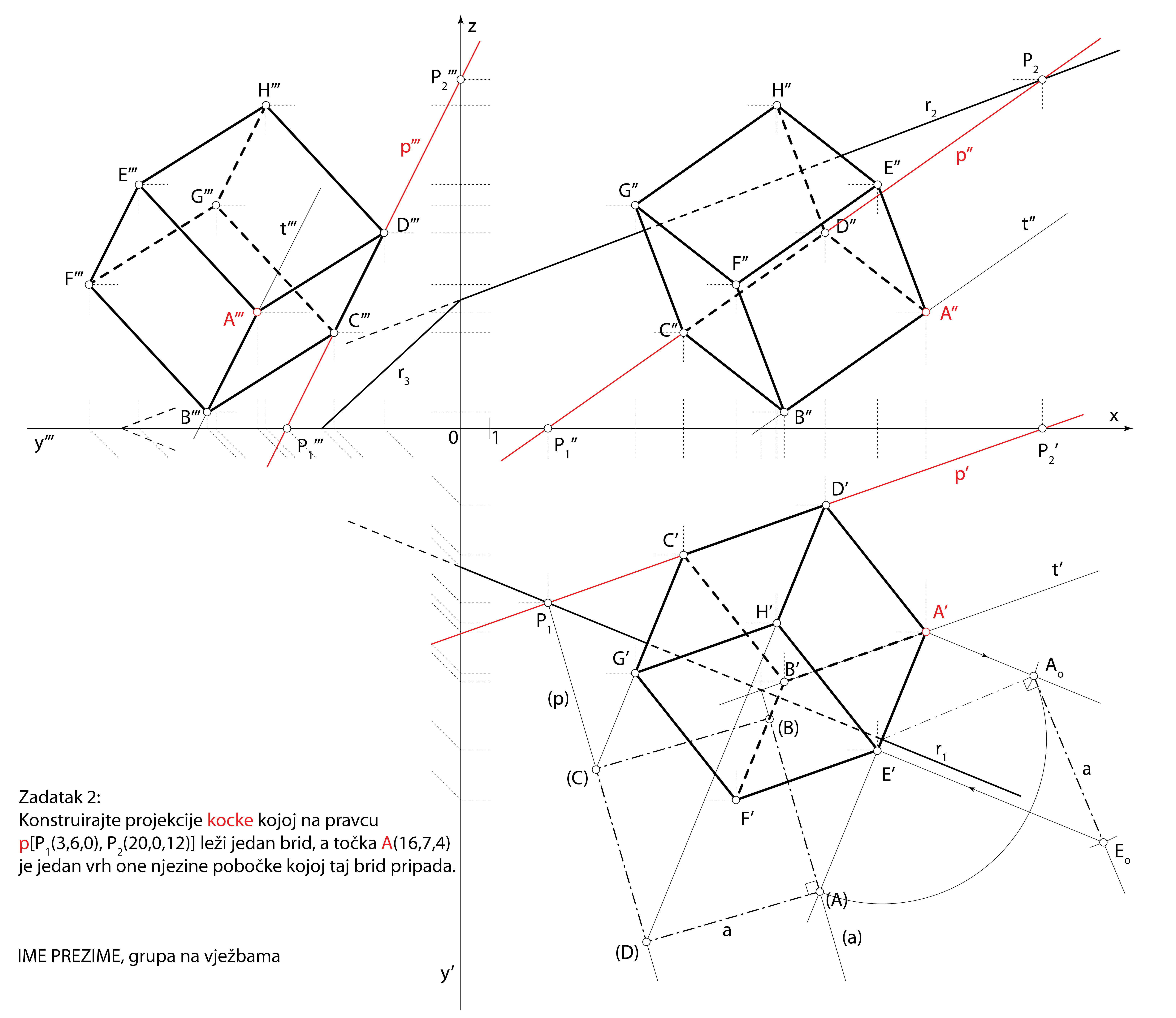
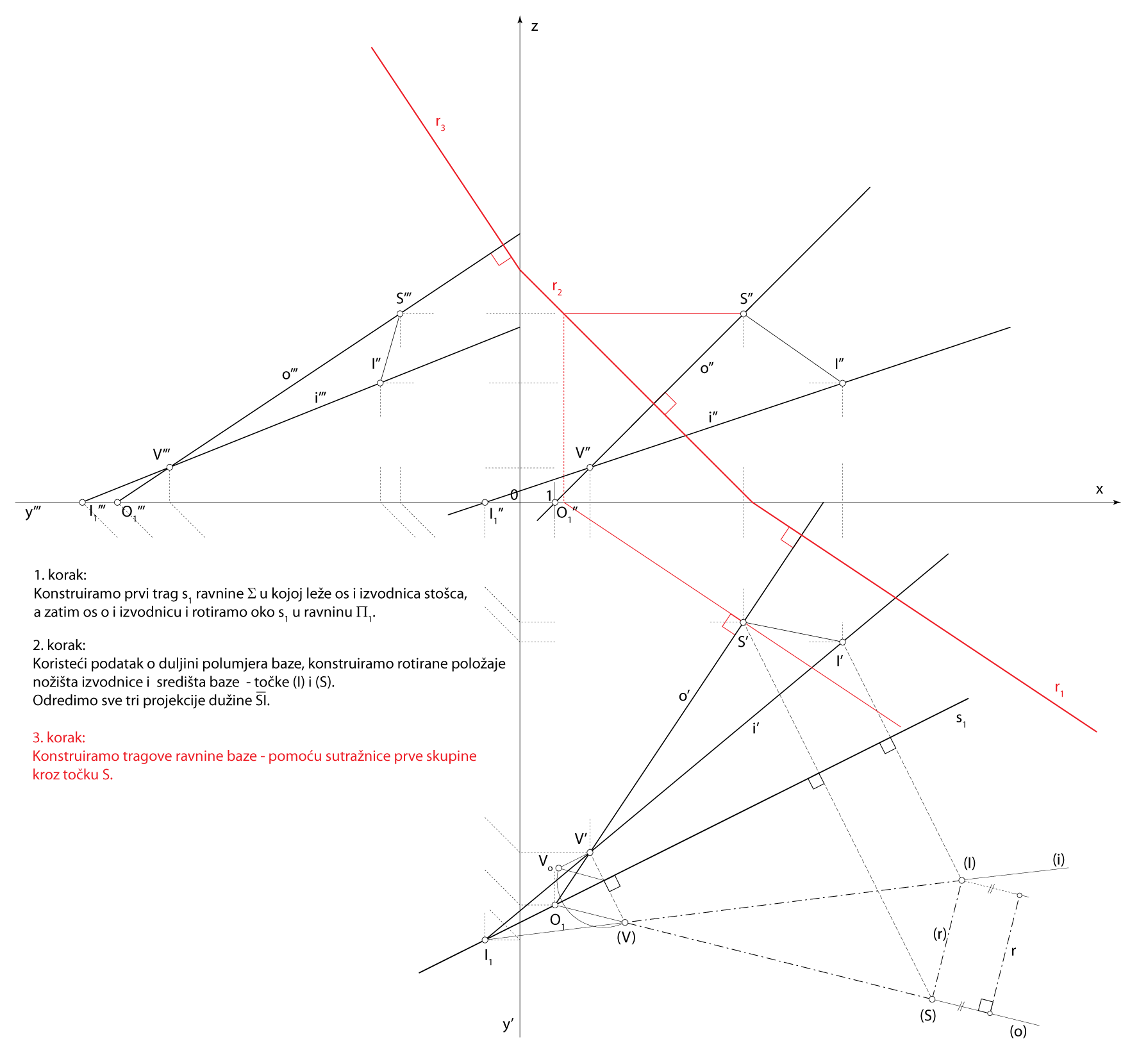
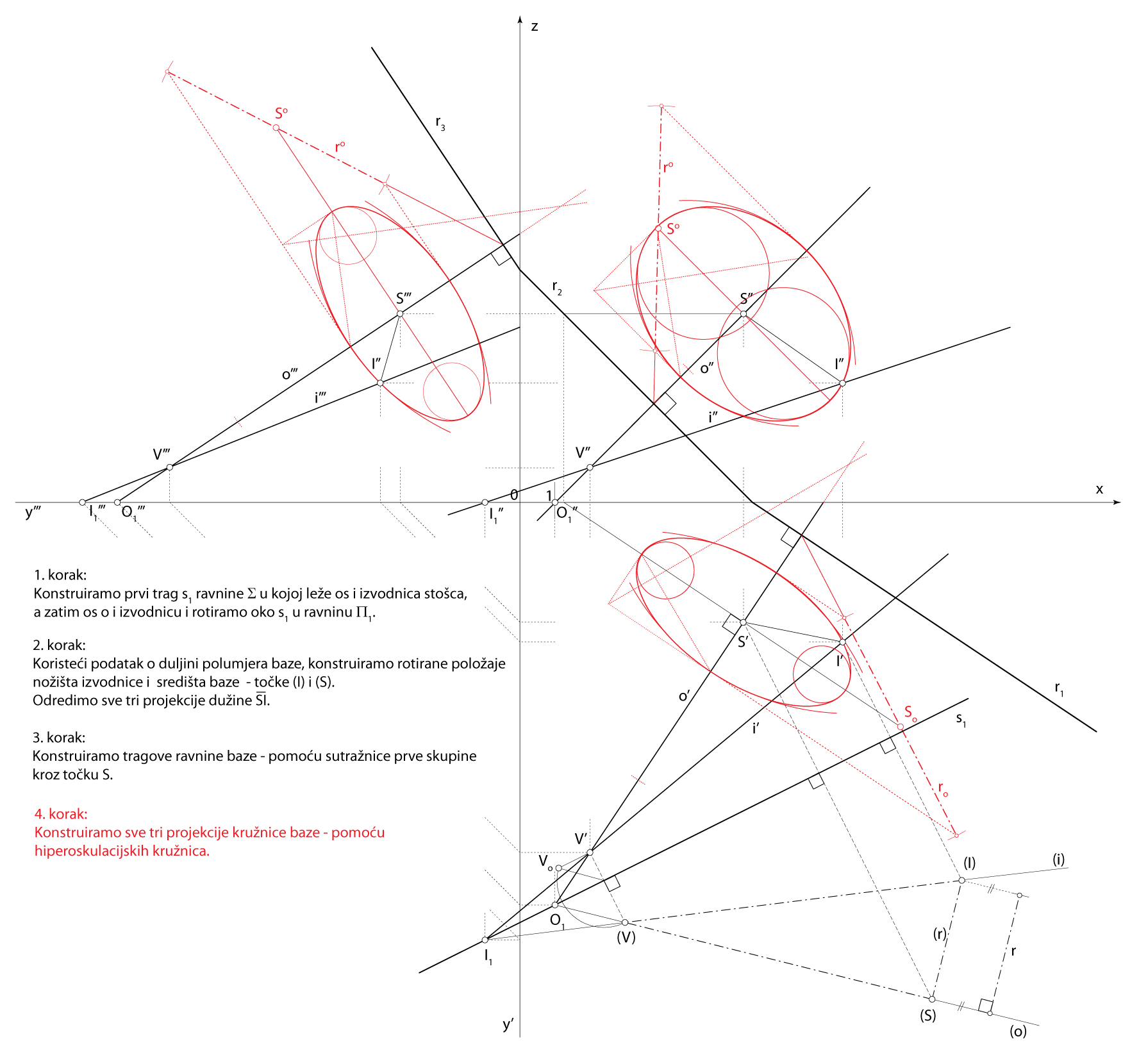
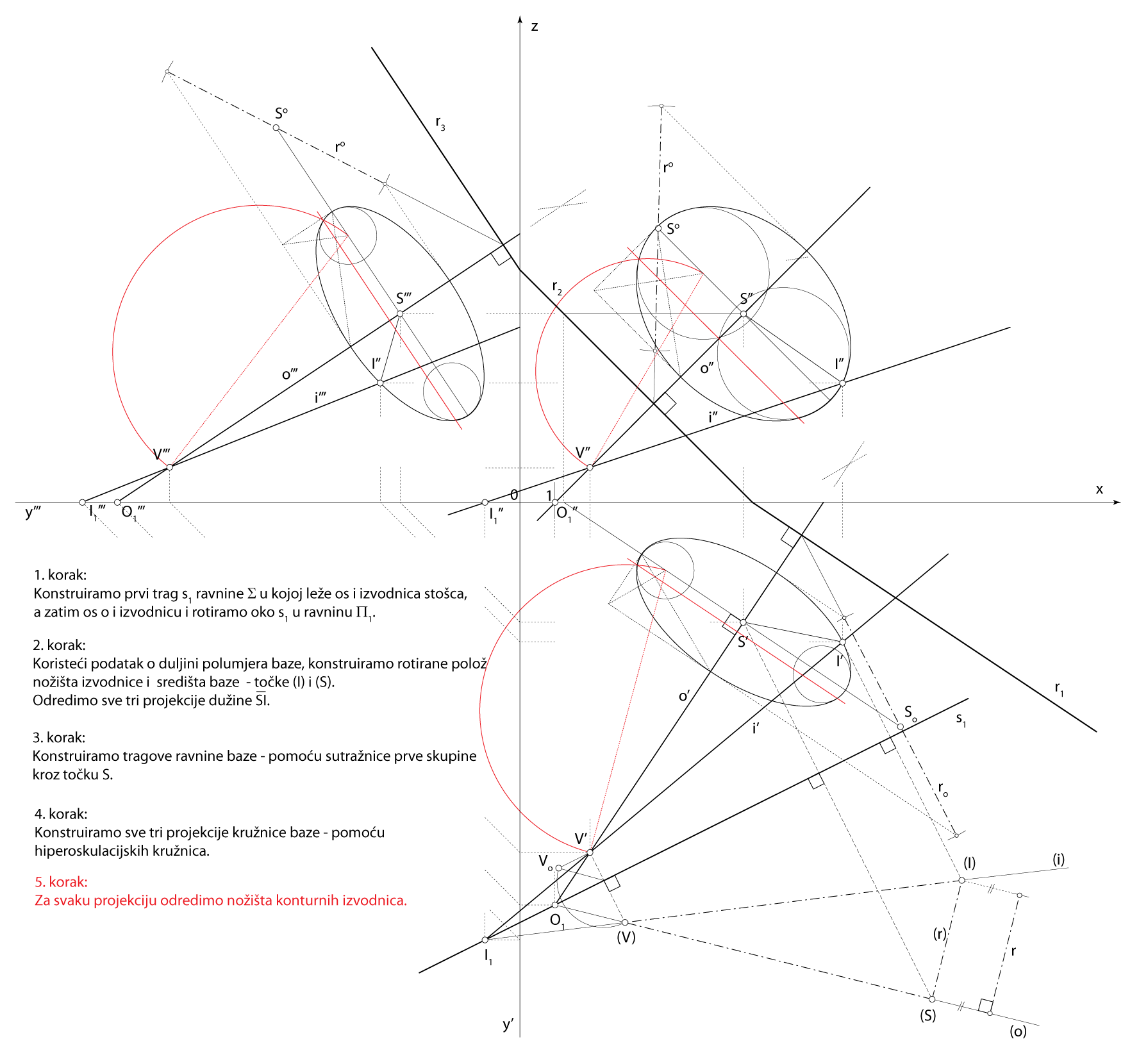
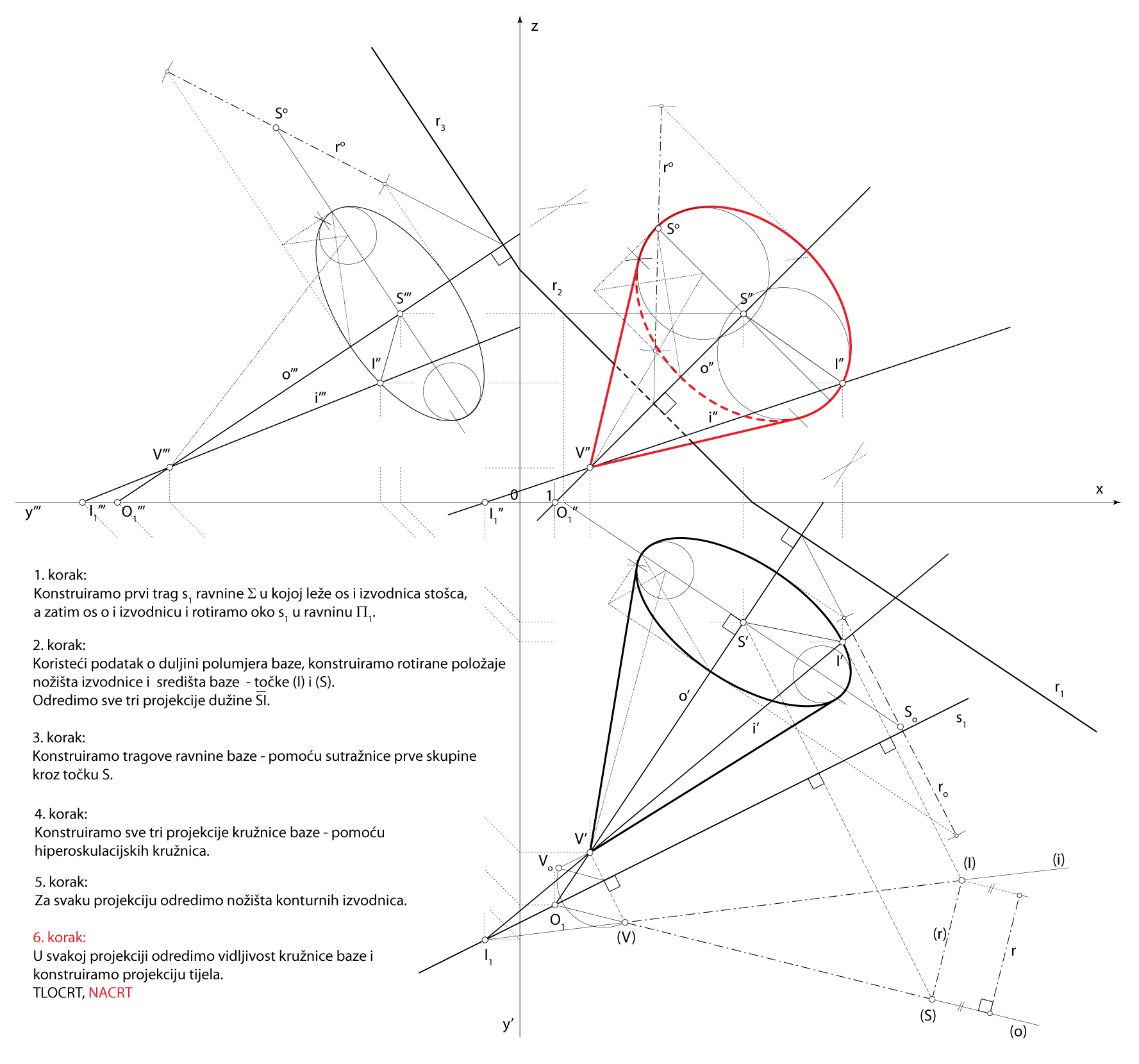
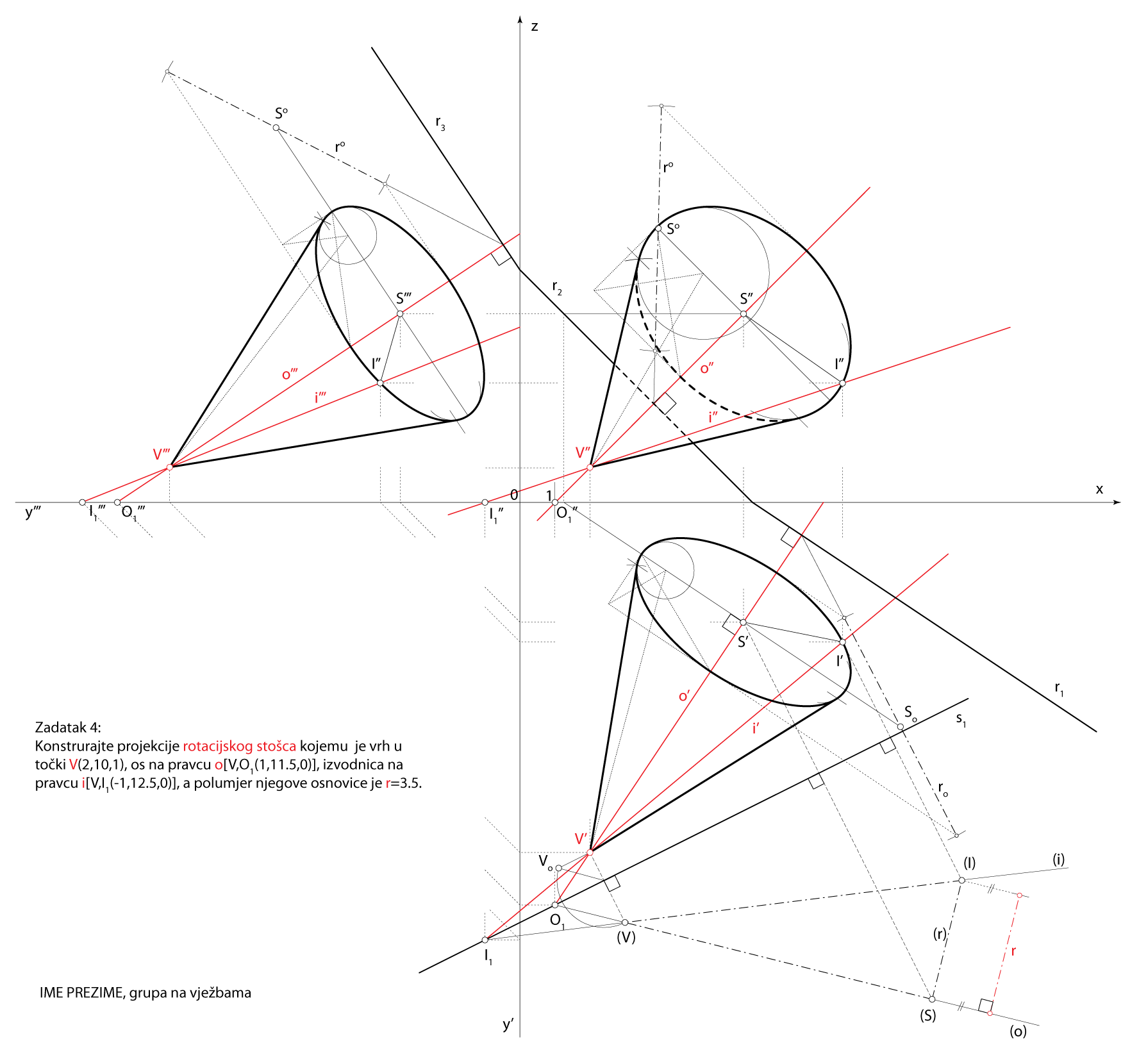
Zadatak 3: Konstruirajte projekcije rotacijskog stošca kojemu je vrh u točki \(\small V(2,10,1)\), os na pravcu \(\small o [V, O_1(1,11.5,0)]\), izvodnica na pravcu \(\small i [V, I_1(-1,12.5,0)]\), a polumjer osnovke je \(\small r=3.5\).
Shema prostornog rješenja
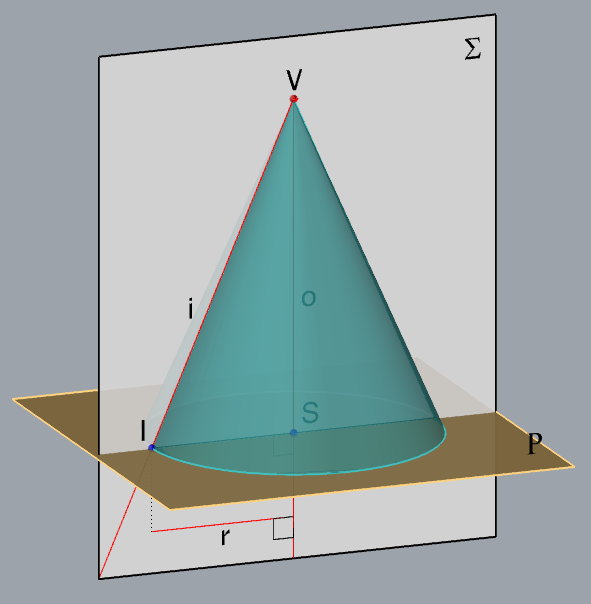
- \(\small \Sigma\) \(\small -\) ravnina osnog presjeka
\(\small o\subset \Sigma\), \(\small i\subset \Sigma\) - \(\small \triangle ISV \subset \Sigma\)
\(\small S-\) središte baze stošca
\(\small I -\) nožište izvodnice \(\small i\) - \(\small\mathrm P\) \(\small -\) ravnina baze
\(\small S\in\) \(\small\mathrm P\), \(\small o \perp \) \(\small\mathrm P\) - Kružnica u ravnini \(\small\mathrm P\), kojoj je središte u točki \(\small S\), a polumjer \(\small \overline{SI}\), kružnica je osnovice zadanog stošca
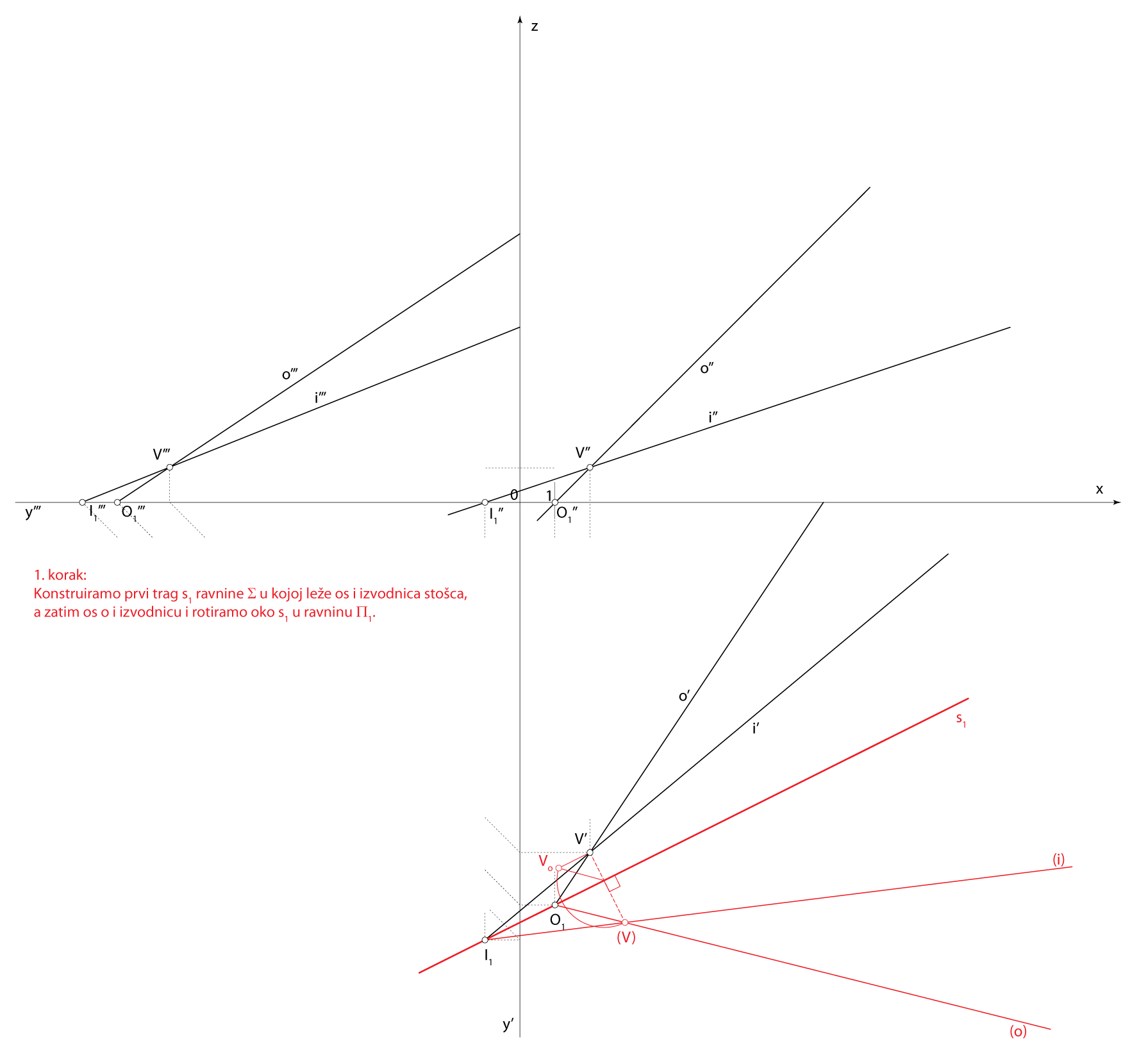
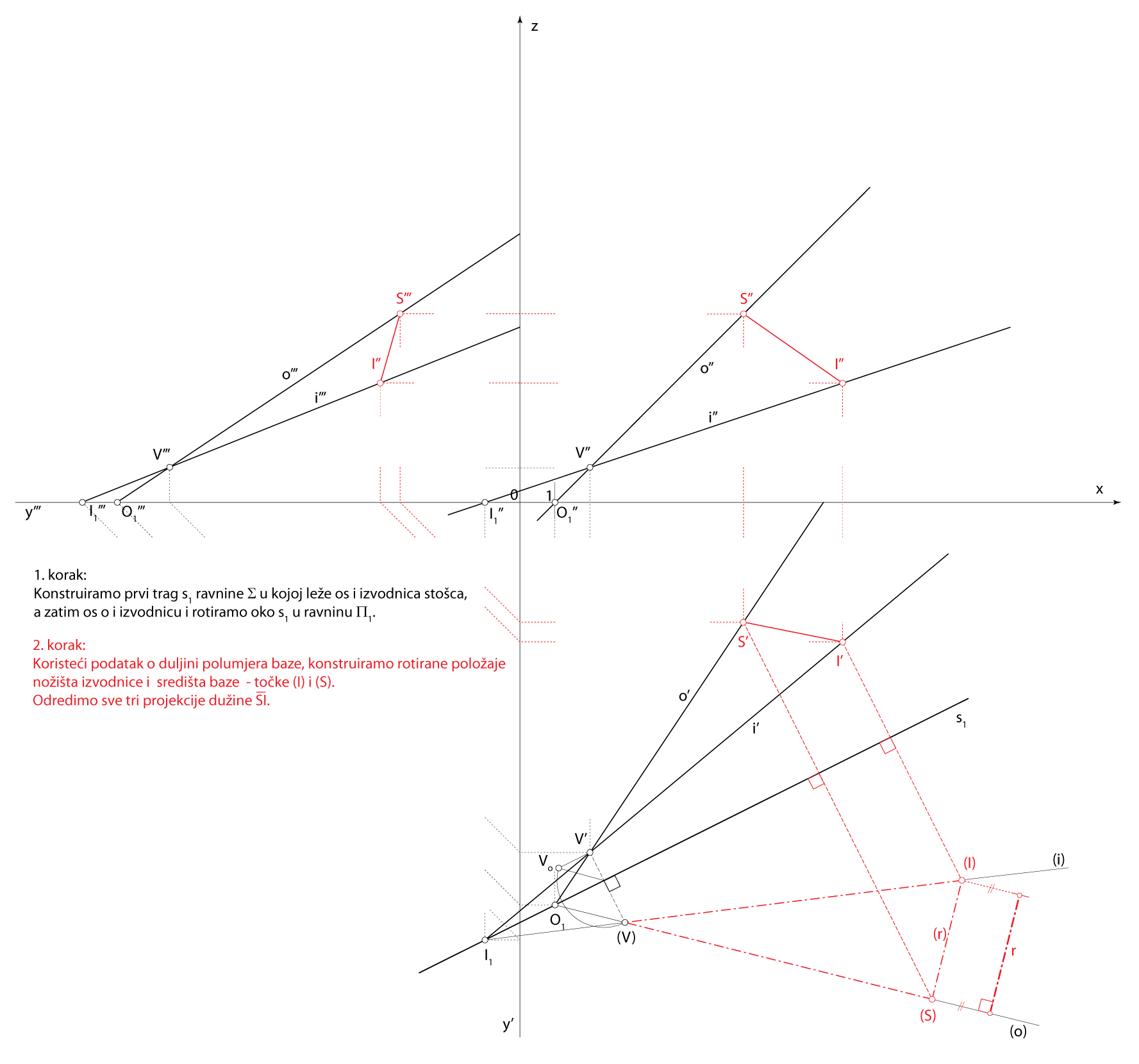
Rješenje u Mongeovoj projekciji (po koracima)
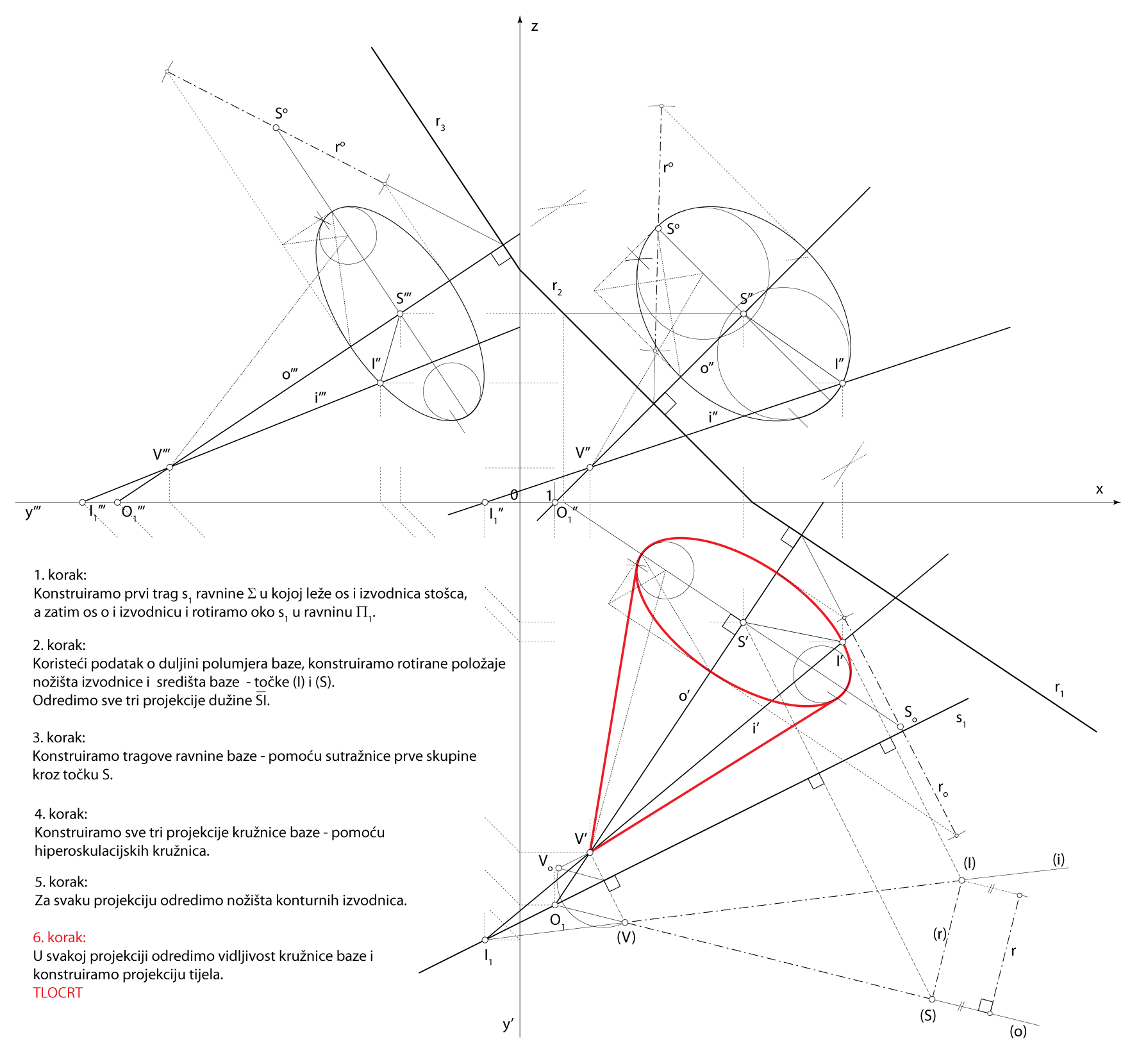
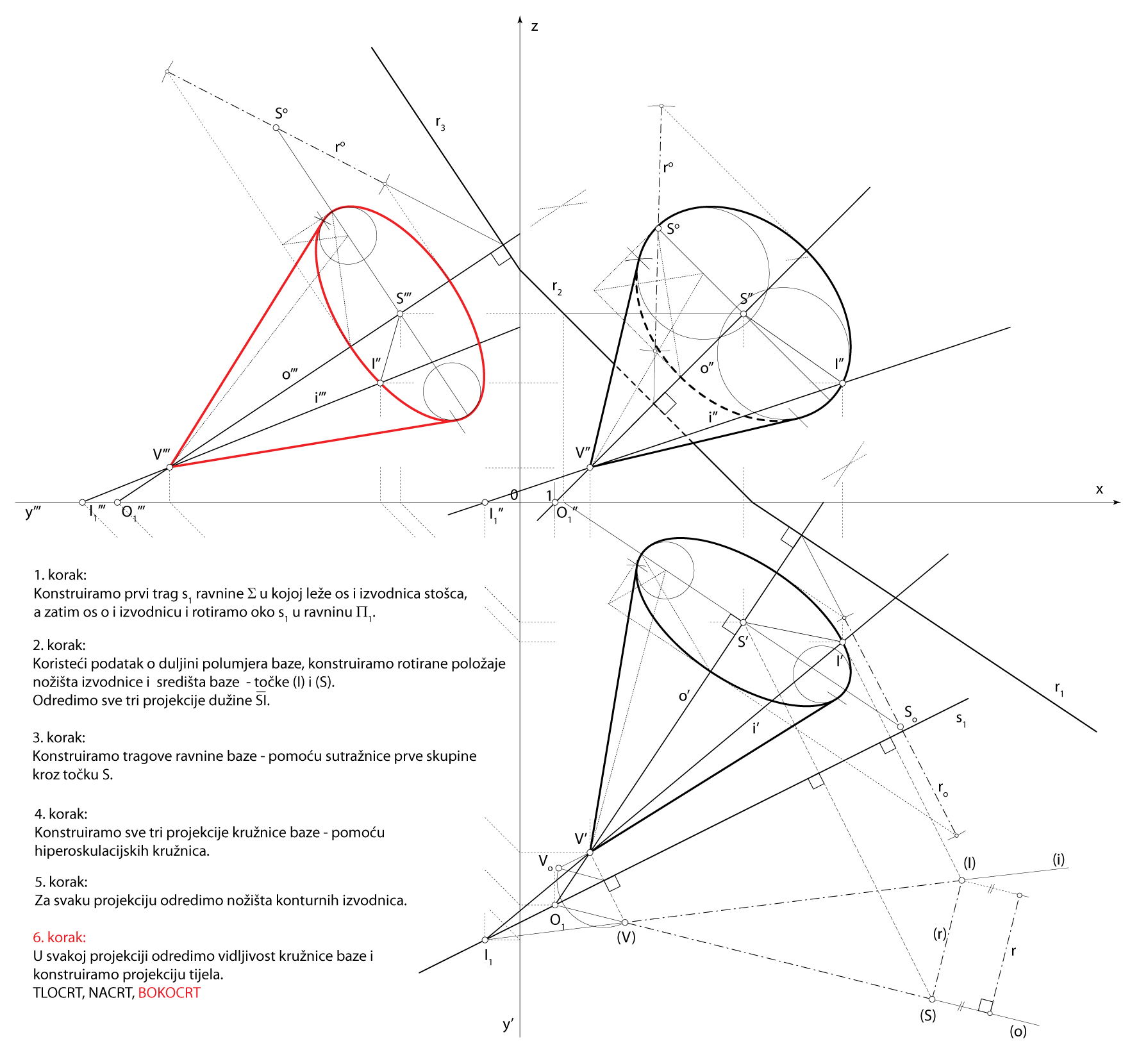
Završni crtež
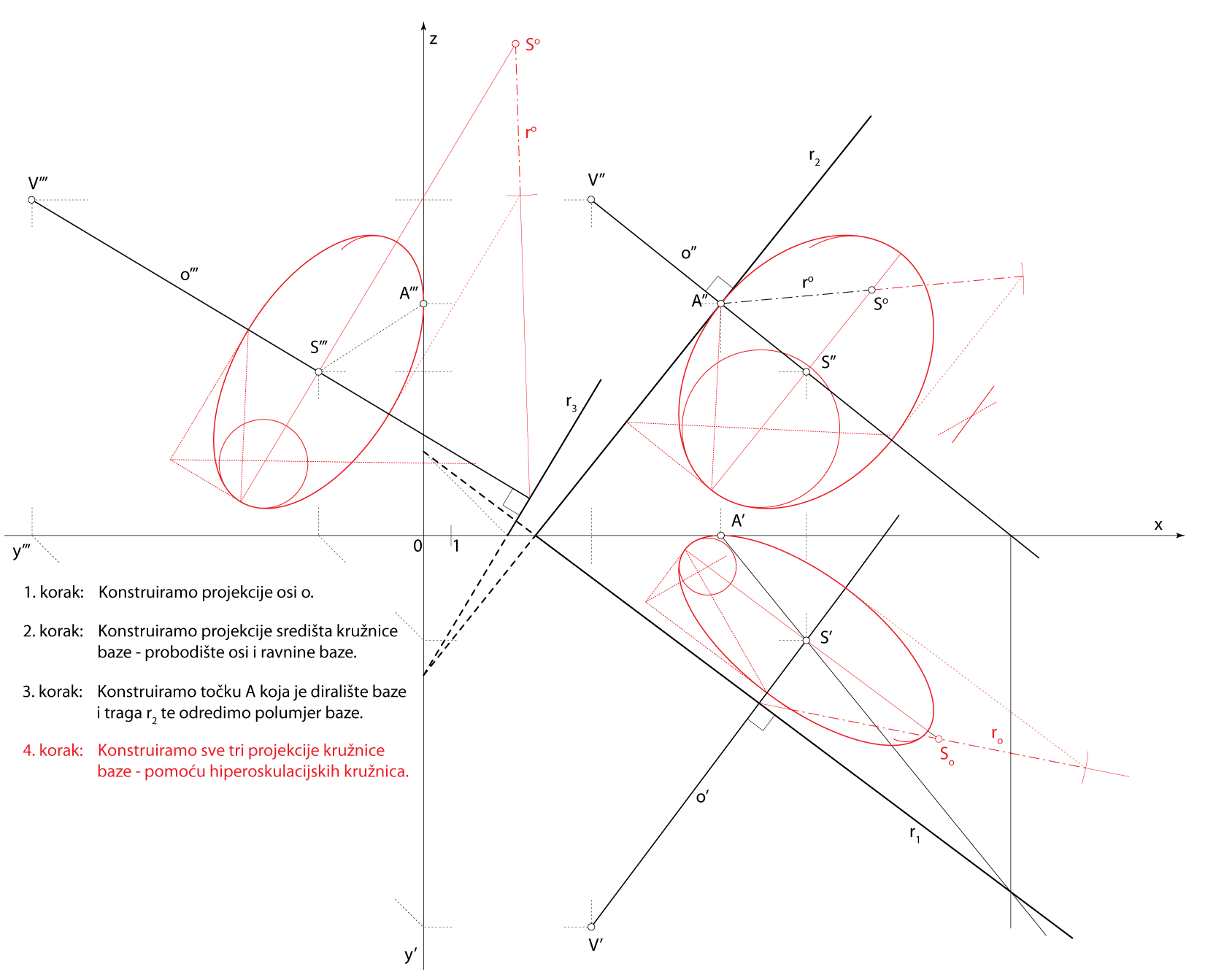
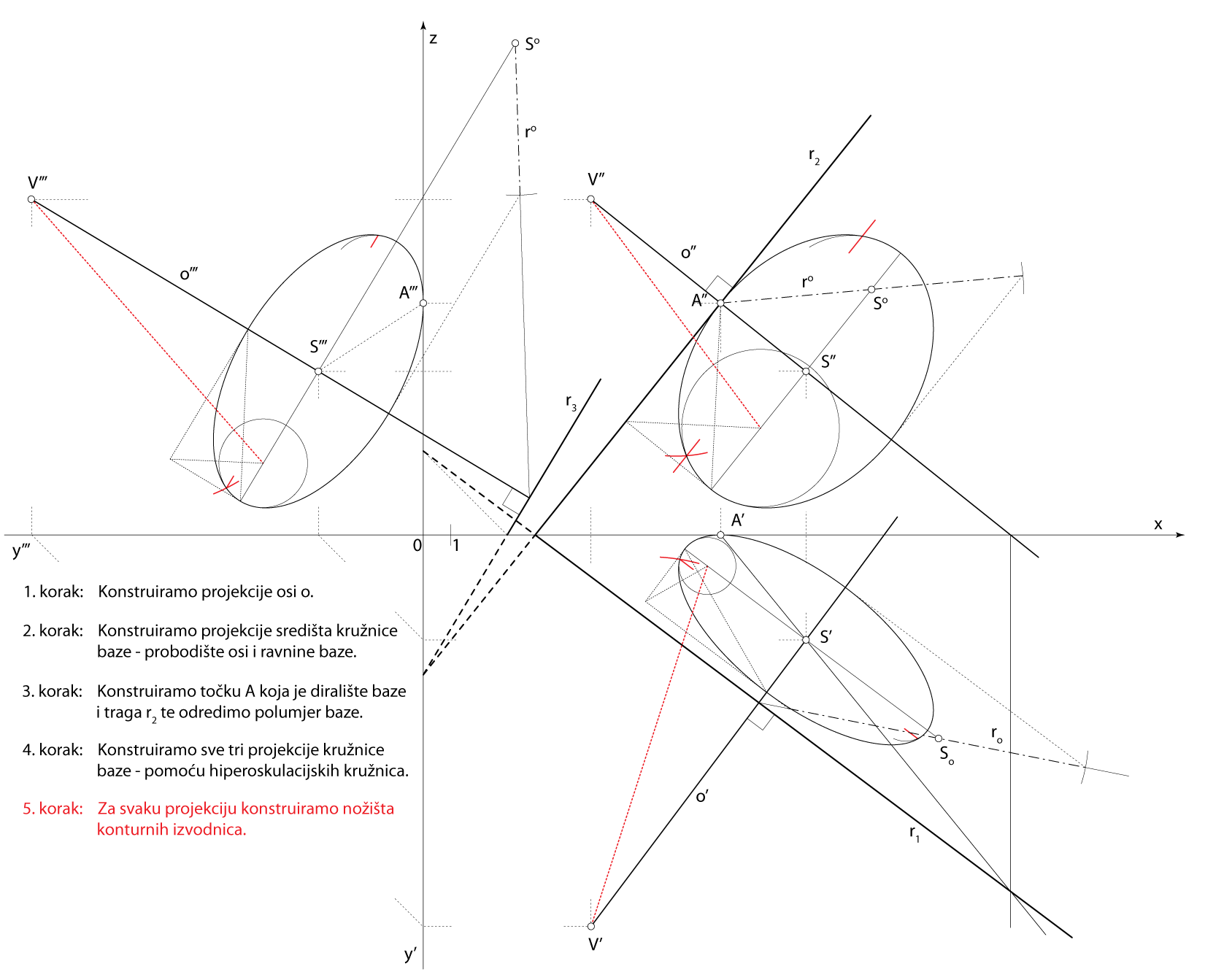
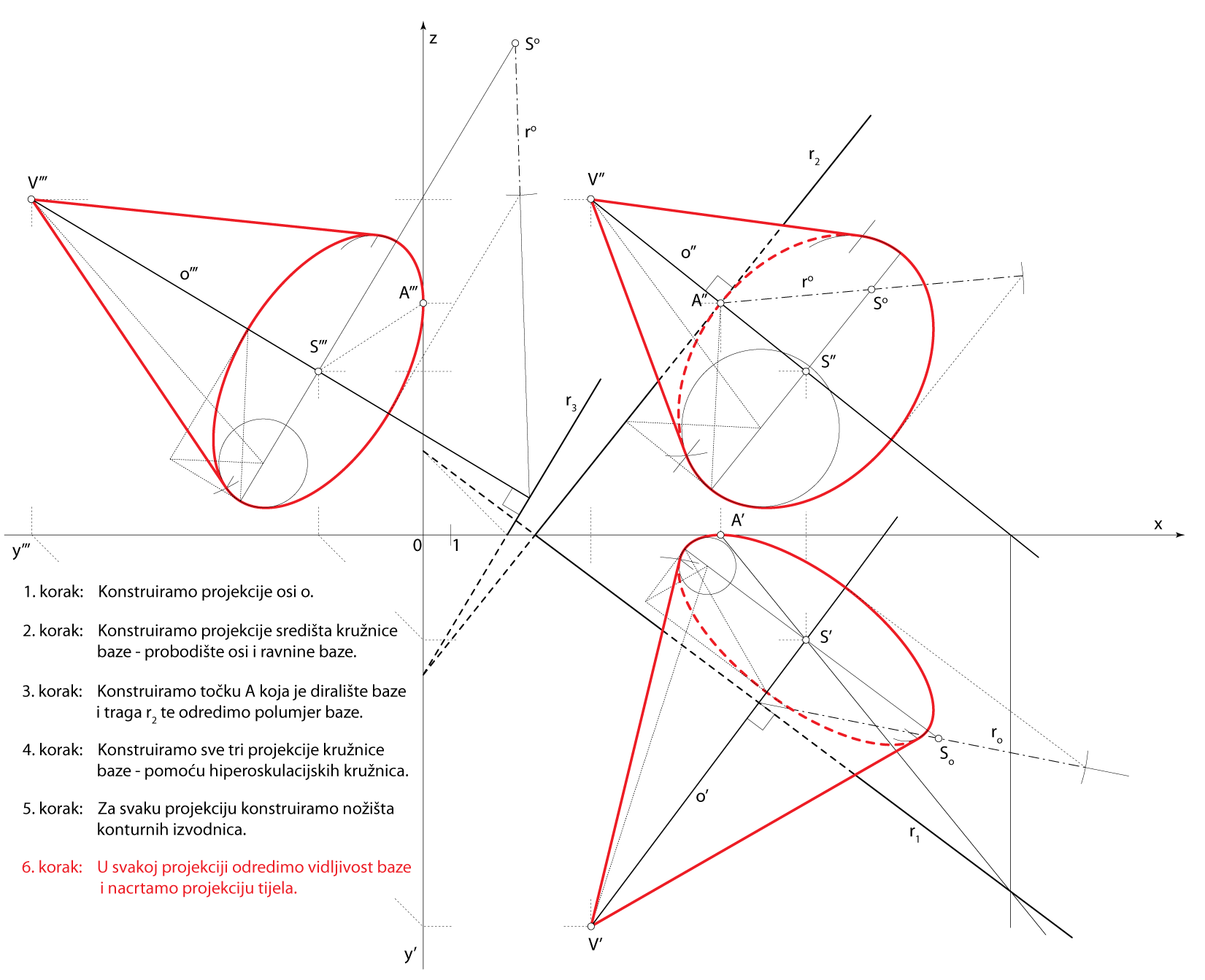
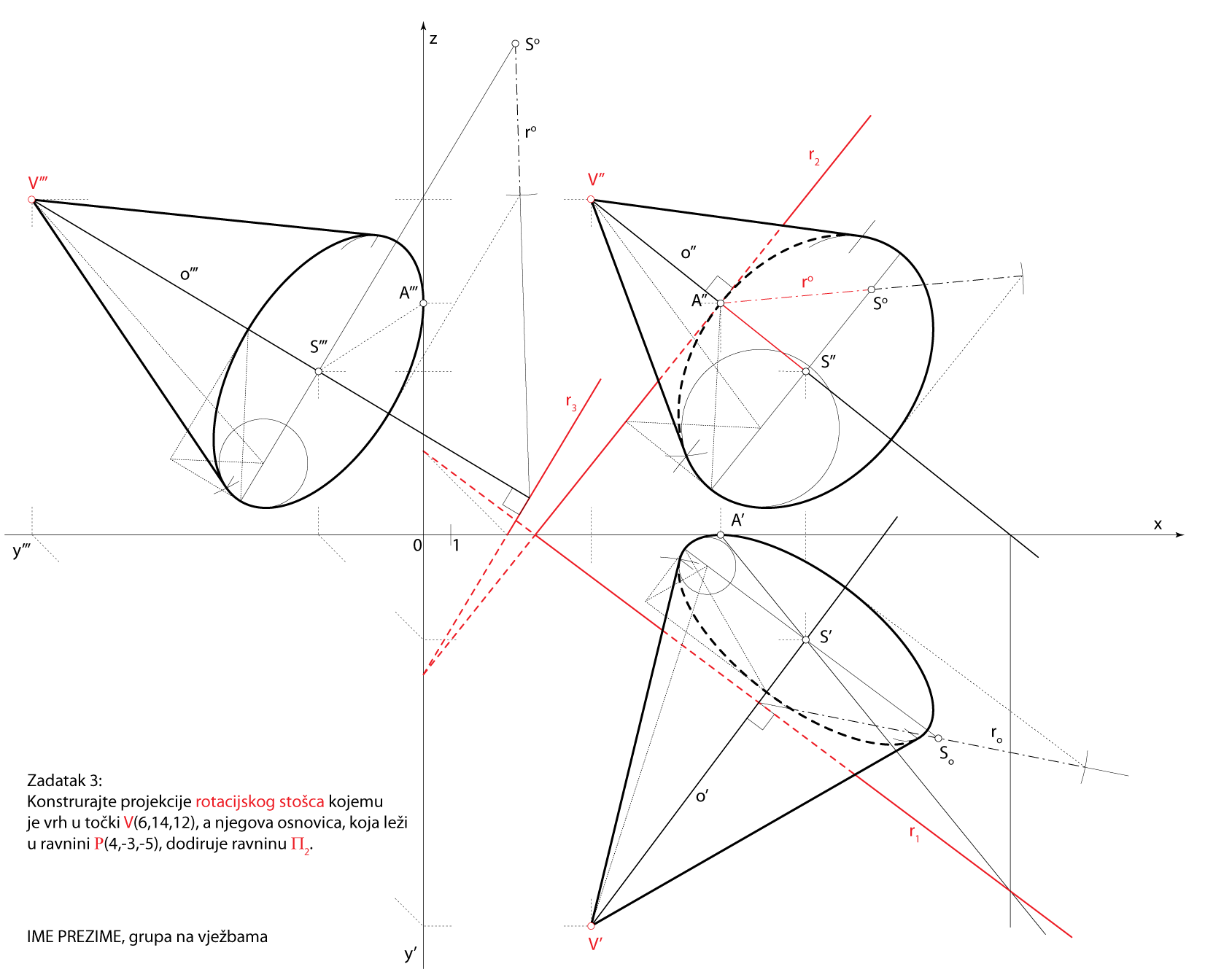
Zadatak 4: Konstrurajte projekcije rotacijskog stošca kojemu je vrh u točki \(\small V(6,14,12)\), a njegova osnovica, koja leži u ravnini \(\small\mathrm P\)\(\small (4,-3,-5)\), dodiruje ravninu \(\small \Pi_2\).
Shema prostornog rješenja
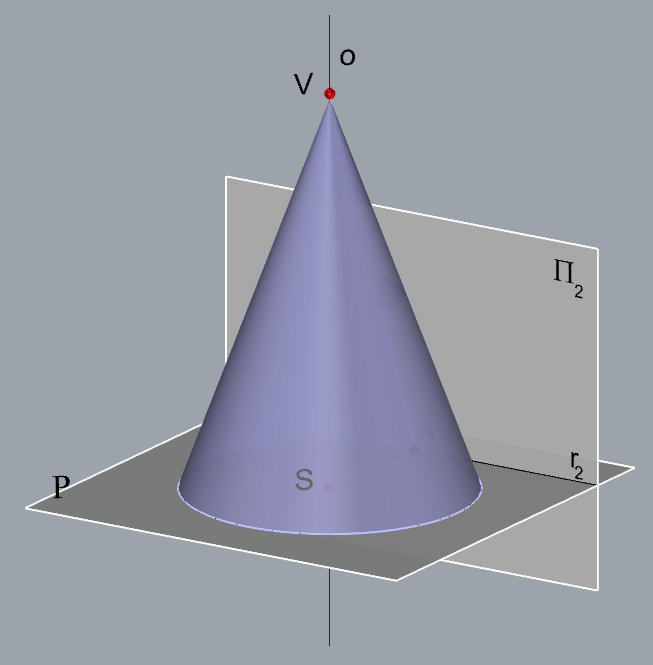
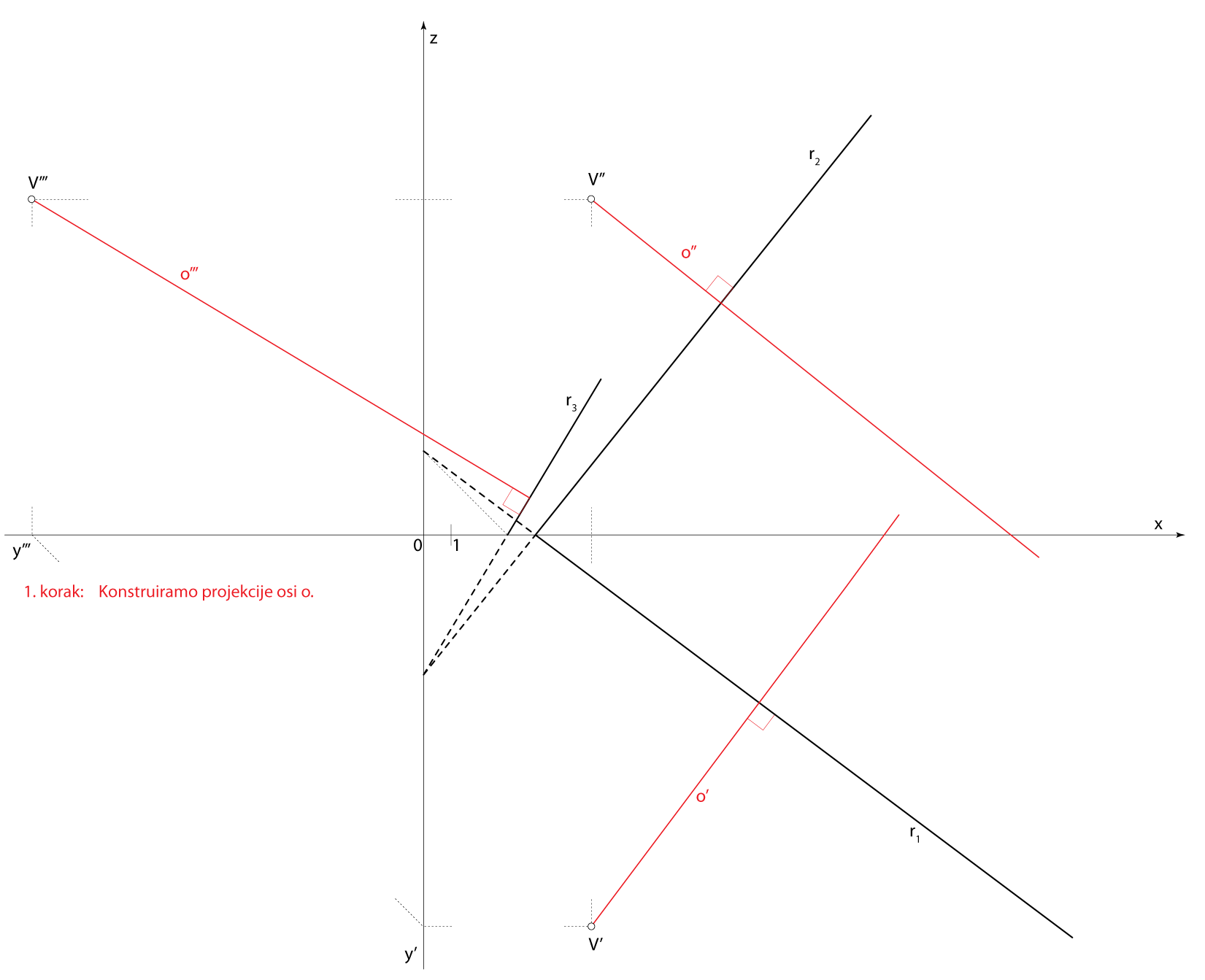
- \(\small o \,-\) os rotacijskog stošca
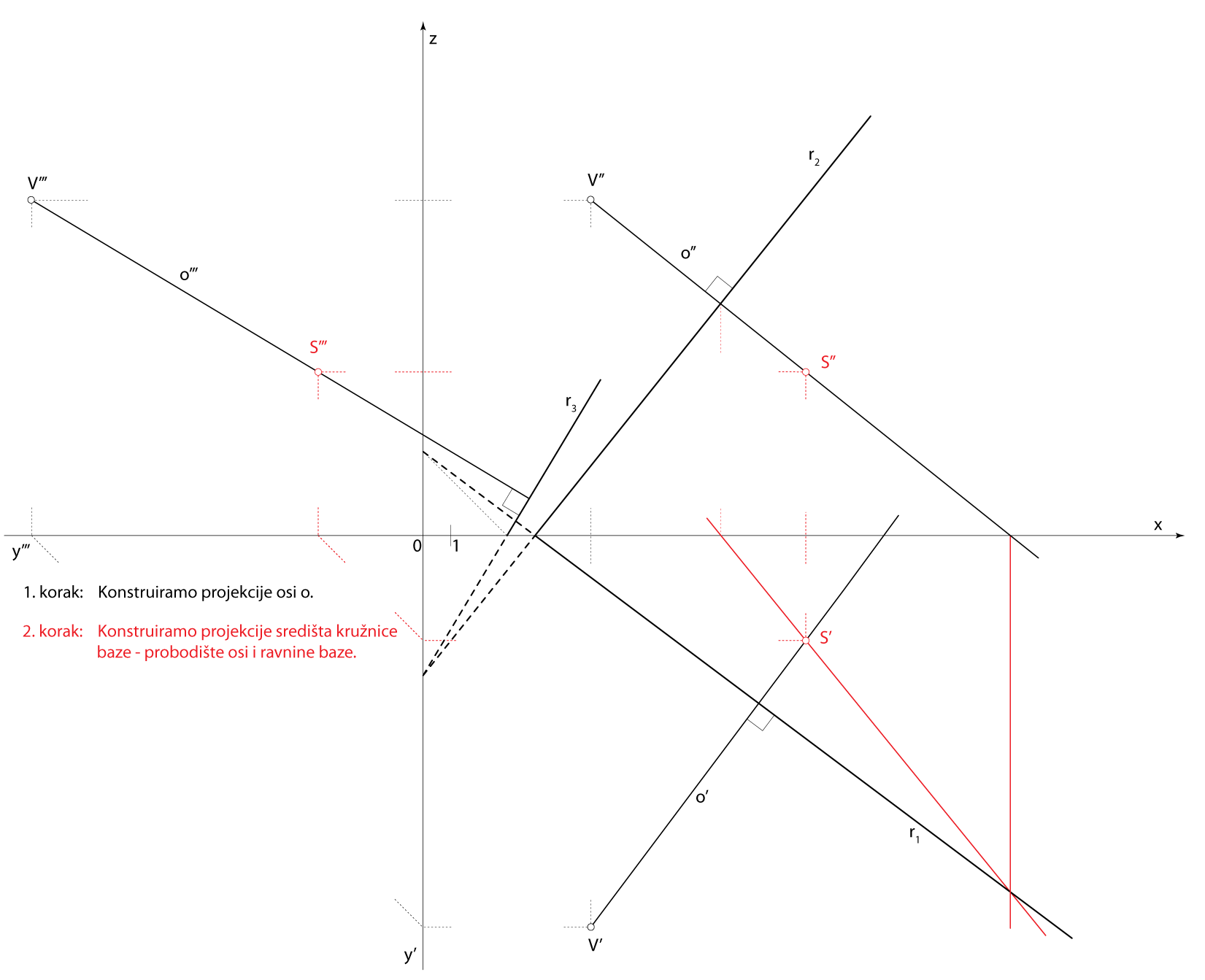
\(\small V\in o\), \(\small o \perp\,\) \(\small\mathrm P\) - \(\small S \,-\) središte baza stošca
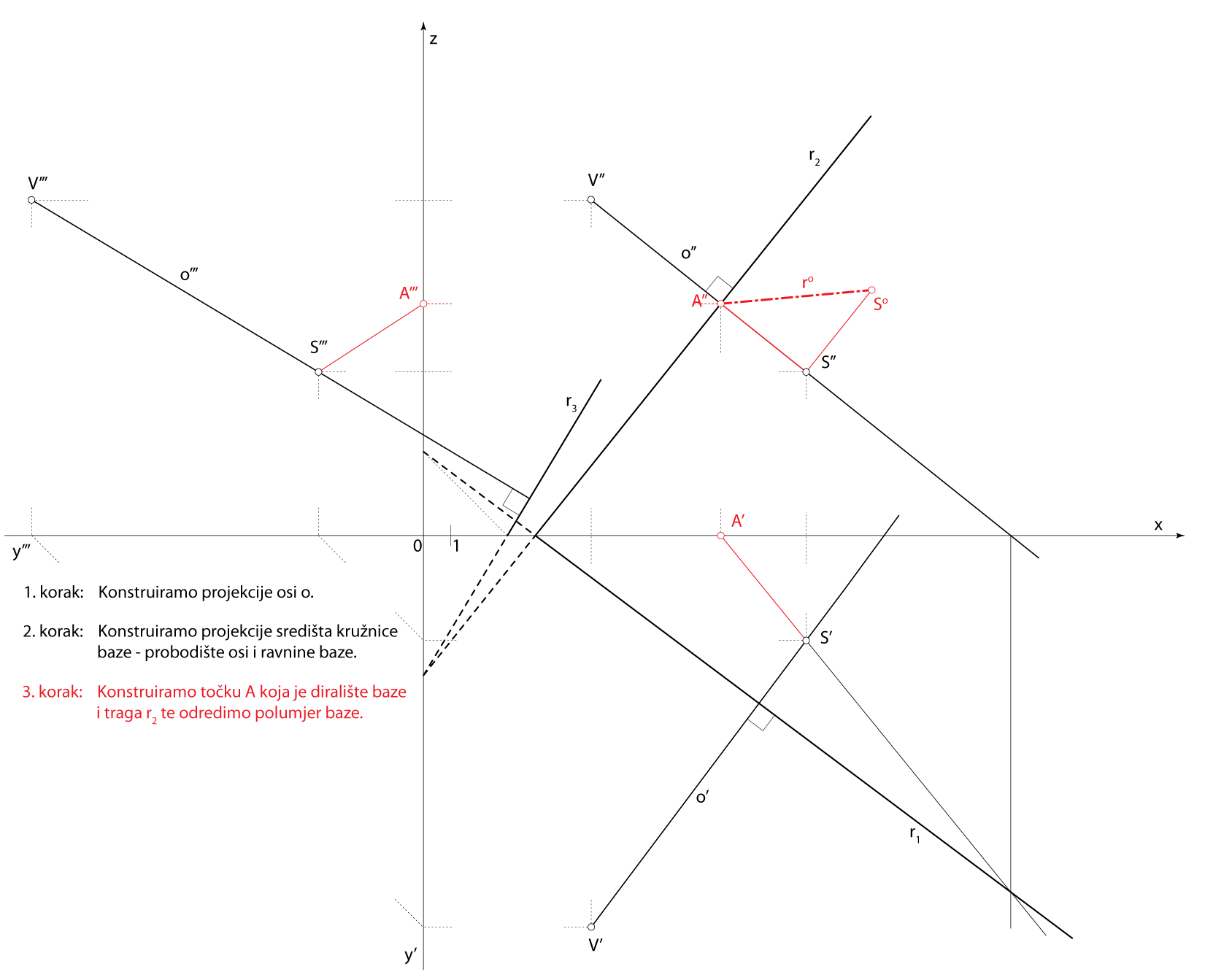
\(\small S=o\cap\,\)\(\small\mathrm P\) - \(\small A \,-\) točka na kružnici baze
\(\small A\in r_2\), \(\small SA\,\perp\,r_2\) - Kružnica u ravnini \(\small\mathrm P\), kojoj je \(\small S\) središte, a \(\small \overline{SA}\) polumjer, rub je osnovice zadanog stošca
Rješenje u Mongeovoj projekciji (po koracima)
Završni crtež
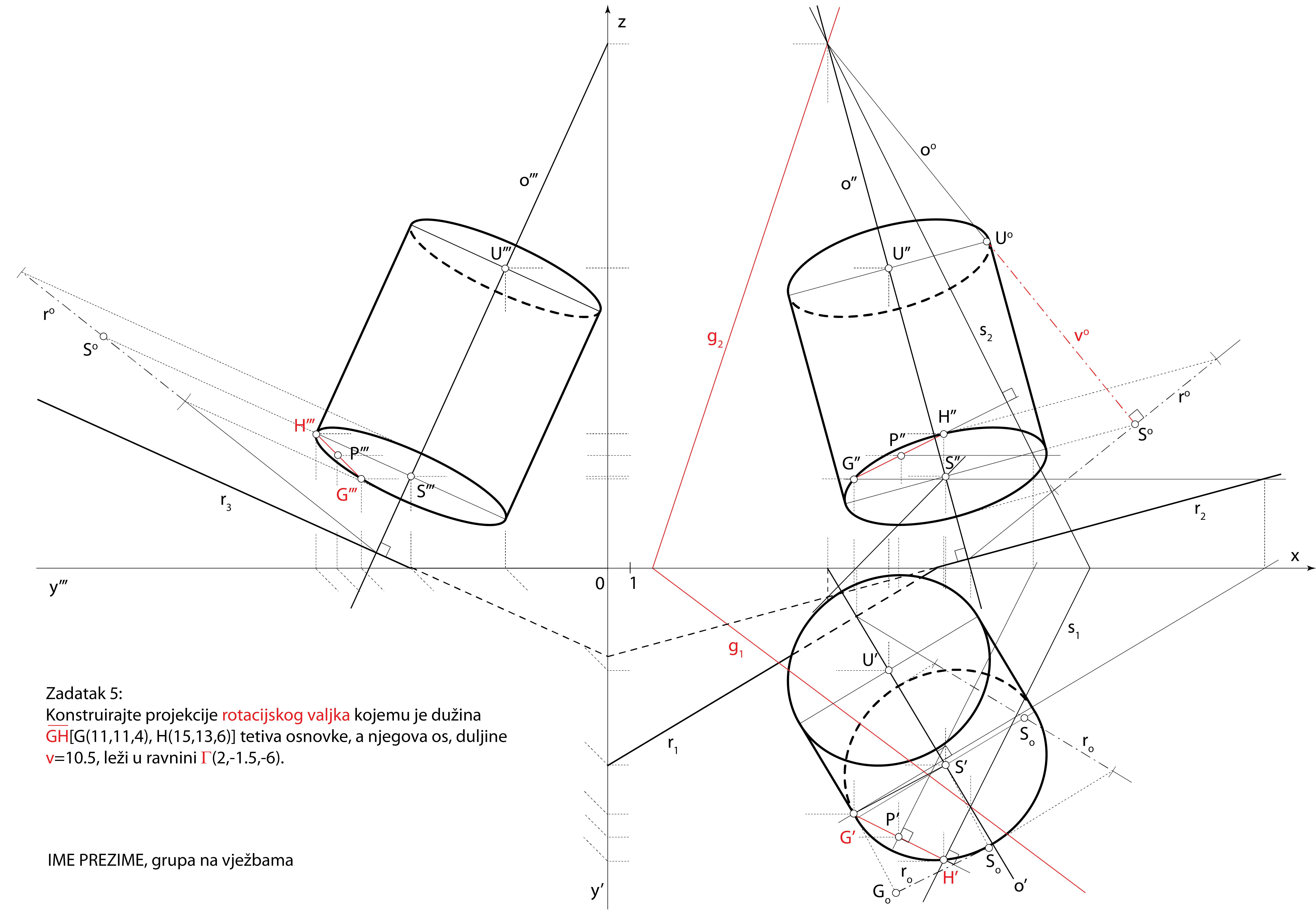
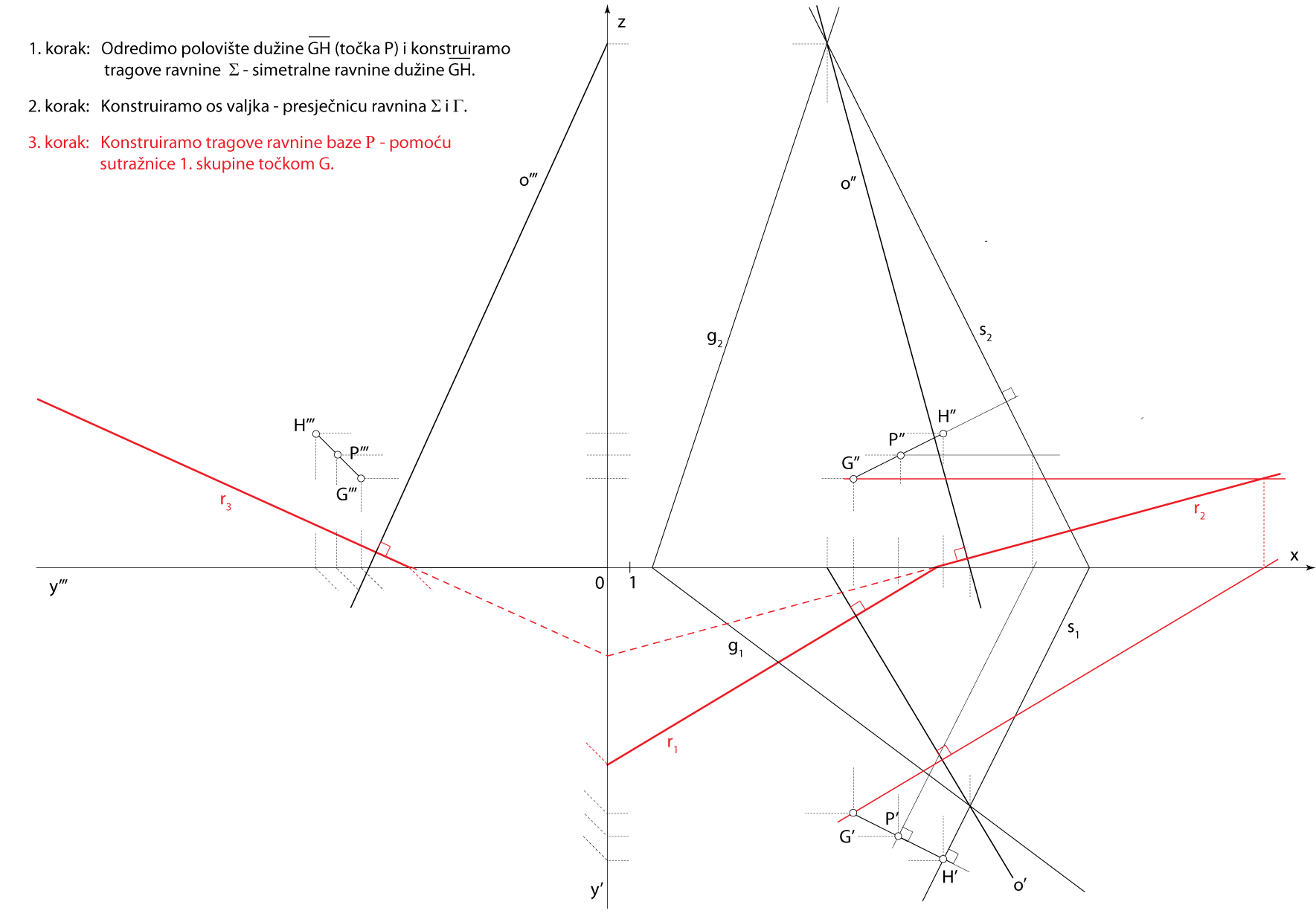
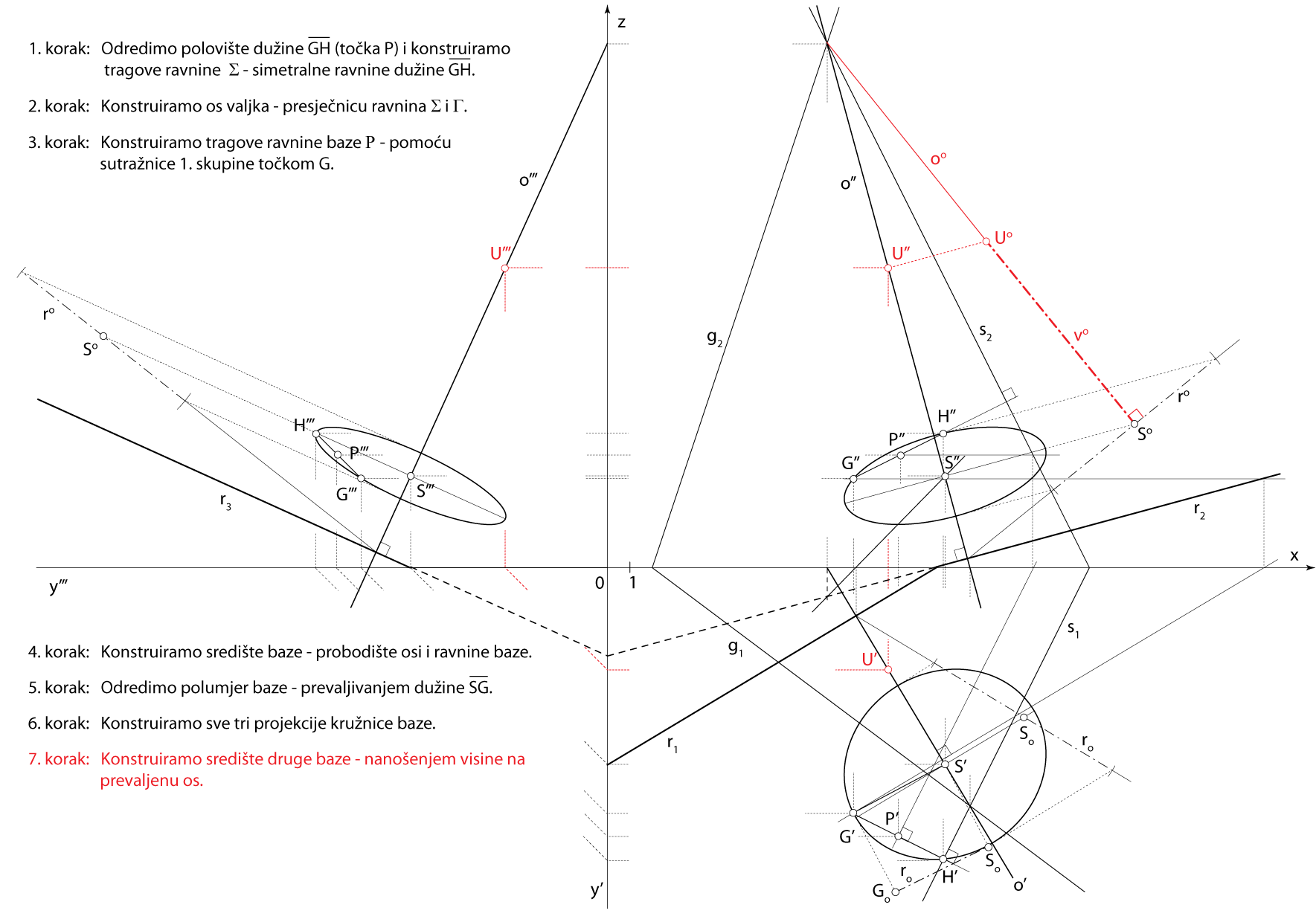
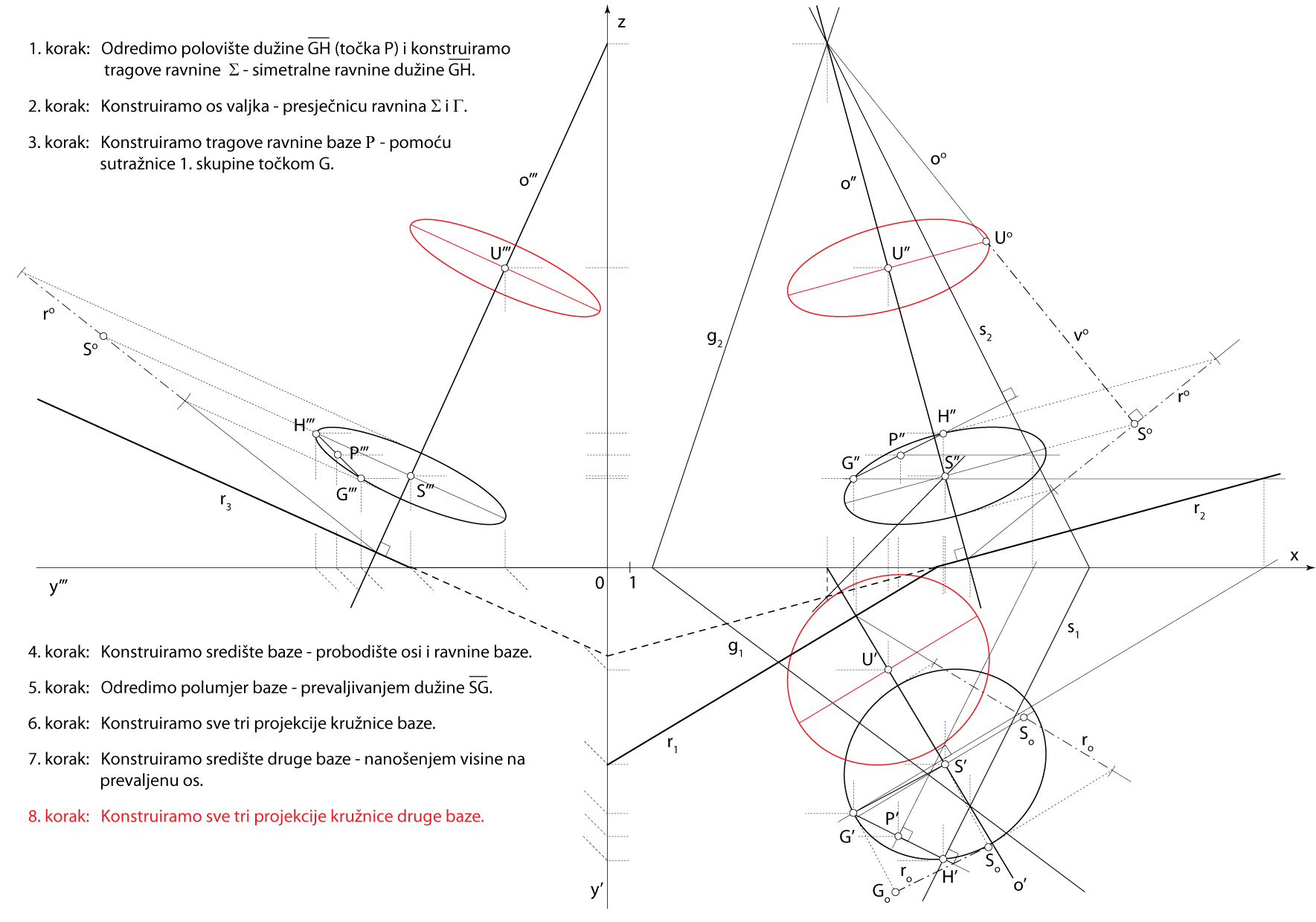
Zadatak 5: Konstruirajte projekcije rotacijskog valjka kojemu je dužina \(\small \overline{GH}[G(11,11,4) , H(15,13,6)]\) tetiva osnovke, a njegova os, duljine \(\small v=10.5\), leži u ravnini \(\small \Gamma(2,-1.5,-6)\).
Shema prostornog rješenja
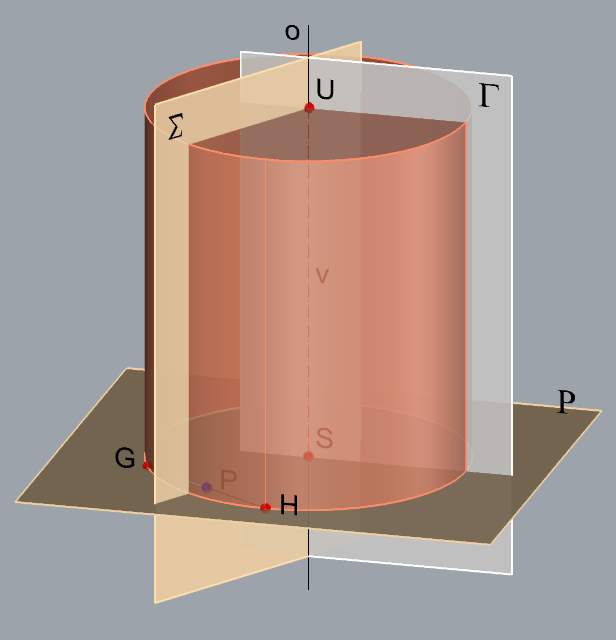
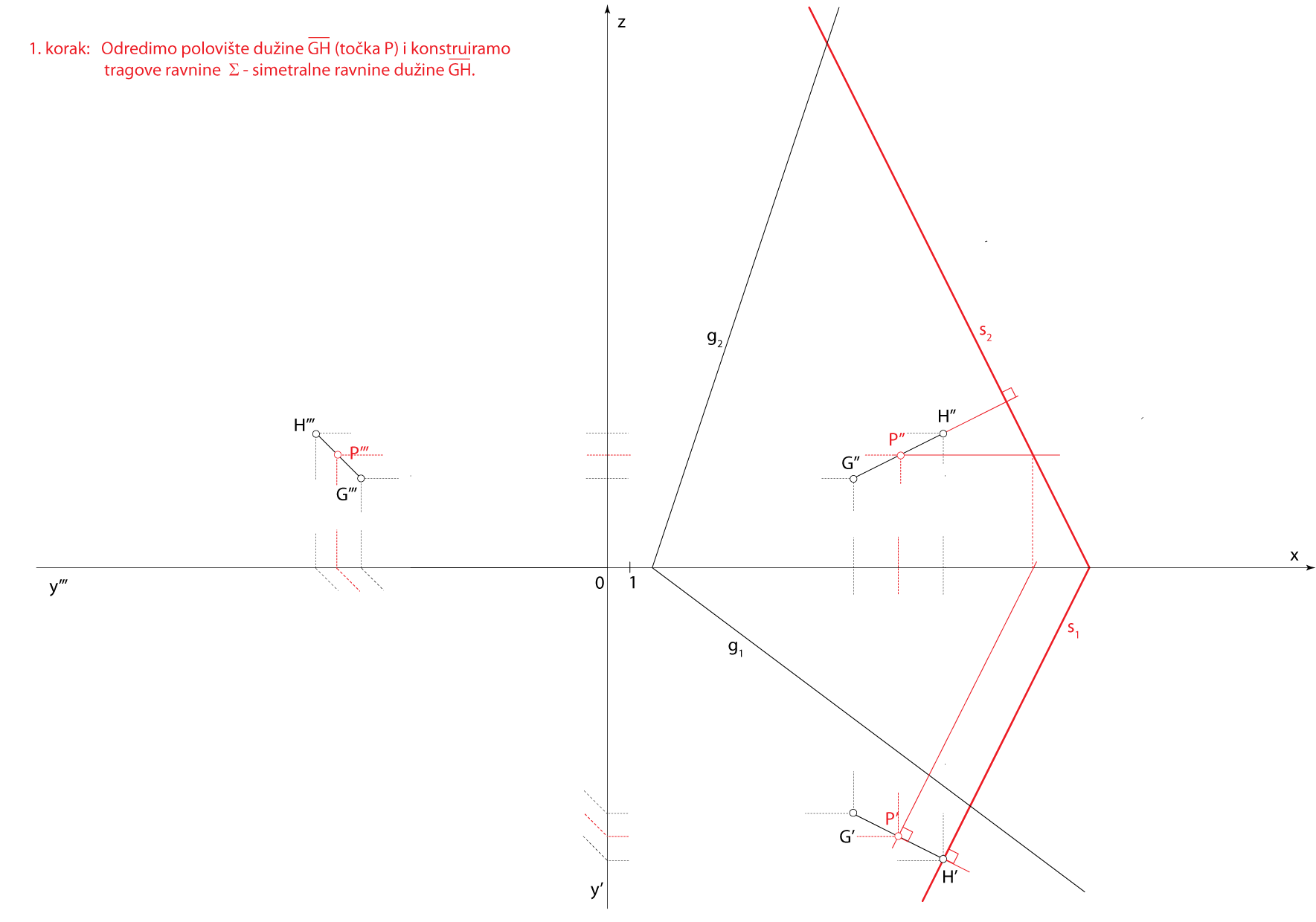
- \(\small \Sigma -\) simetralna ravnina dužine \(\small \overline {GH}\)
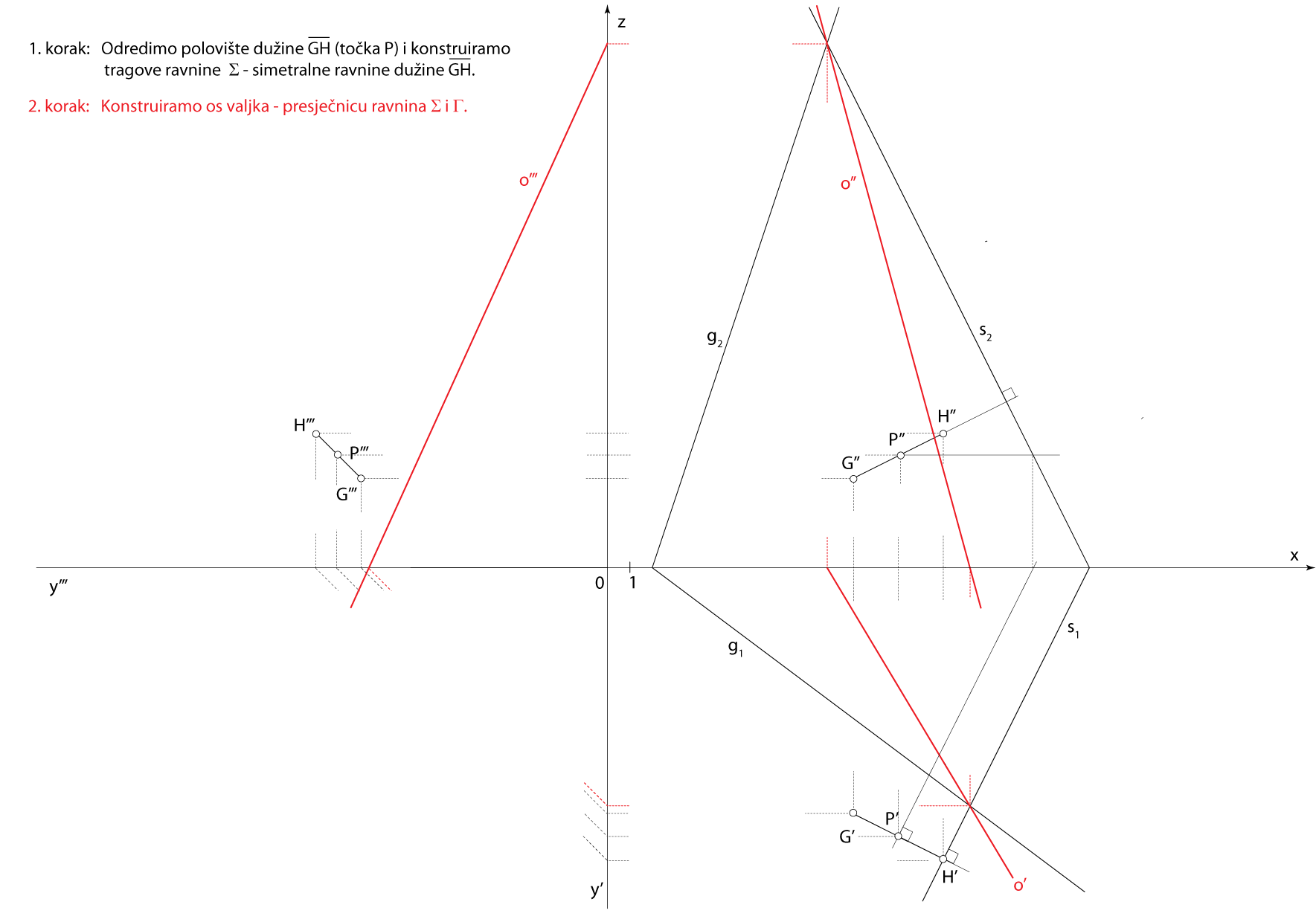
\(\small P -\) polovište \(\small \overline {GH}\), \(\small P \in \Sigma\), \(\small \Sigma\perp GH\) - \(\small o -\) os valjka, \(\small o = \Sigma \cap \Gamma\)
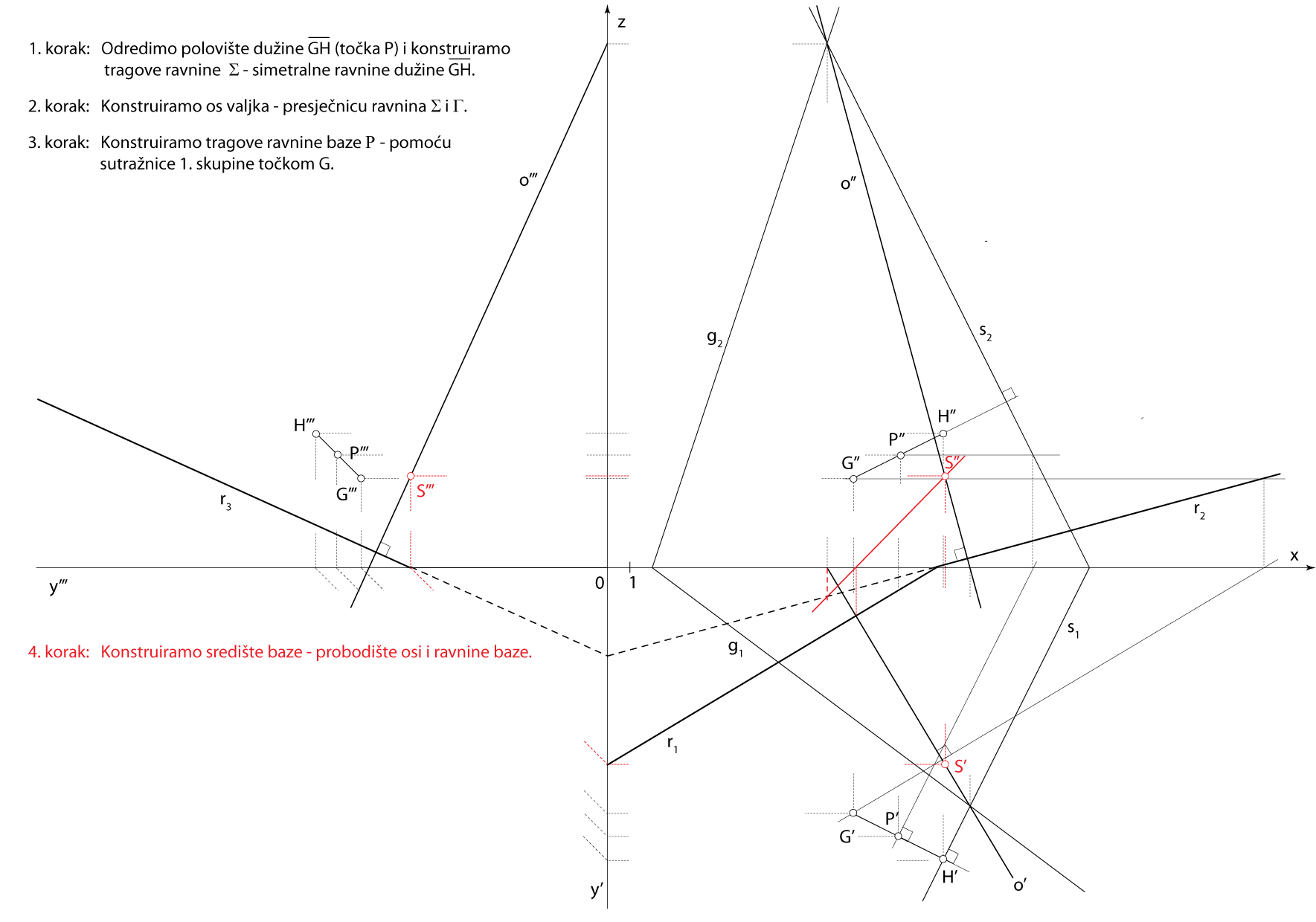
- \(\small\mathrm P\)\(\small -\) ravnina baze, \(\small G\in \) \(\small\mathrm P\), \(\small o \perp \) \(\small\mathrm P\)
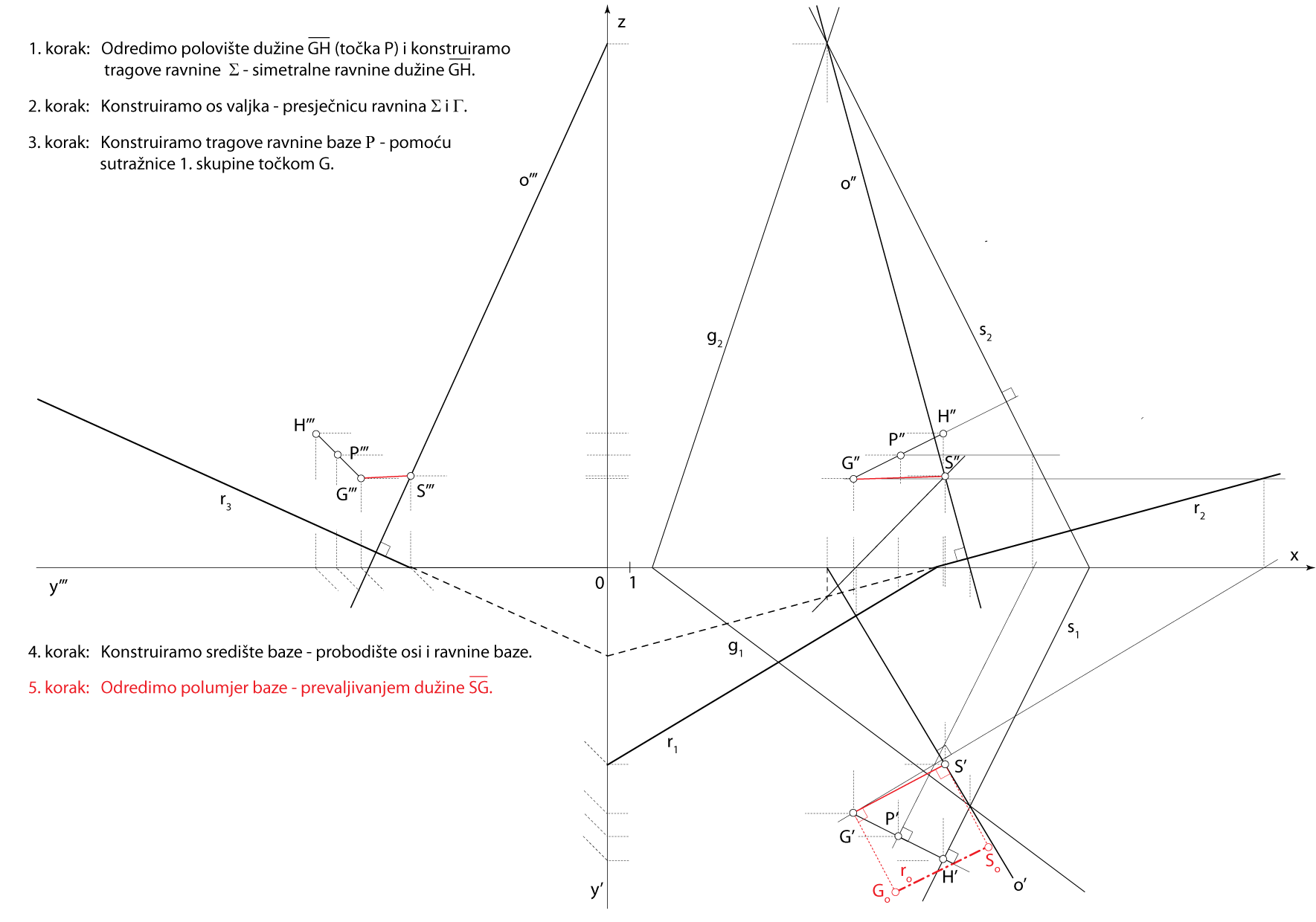
- \(\small S -\) središte baze, \(\small S = o \cap \) \(\small\mathrm P\)
- Kružnica baze leži u ravnini \(\small\mathrm P\), a polumjer joj je \(\small \overline {SG}\)
- \(\small U -\) središte druge baze
\(\small U \in o \), \(\small d(S,U)=v\)
Rješenje u Mongeovoj projekciji (po koracima)
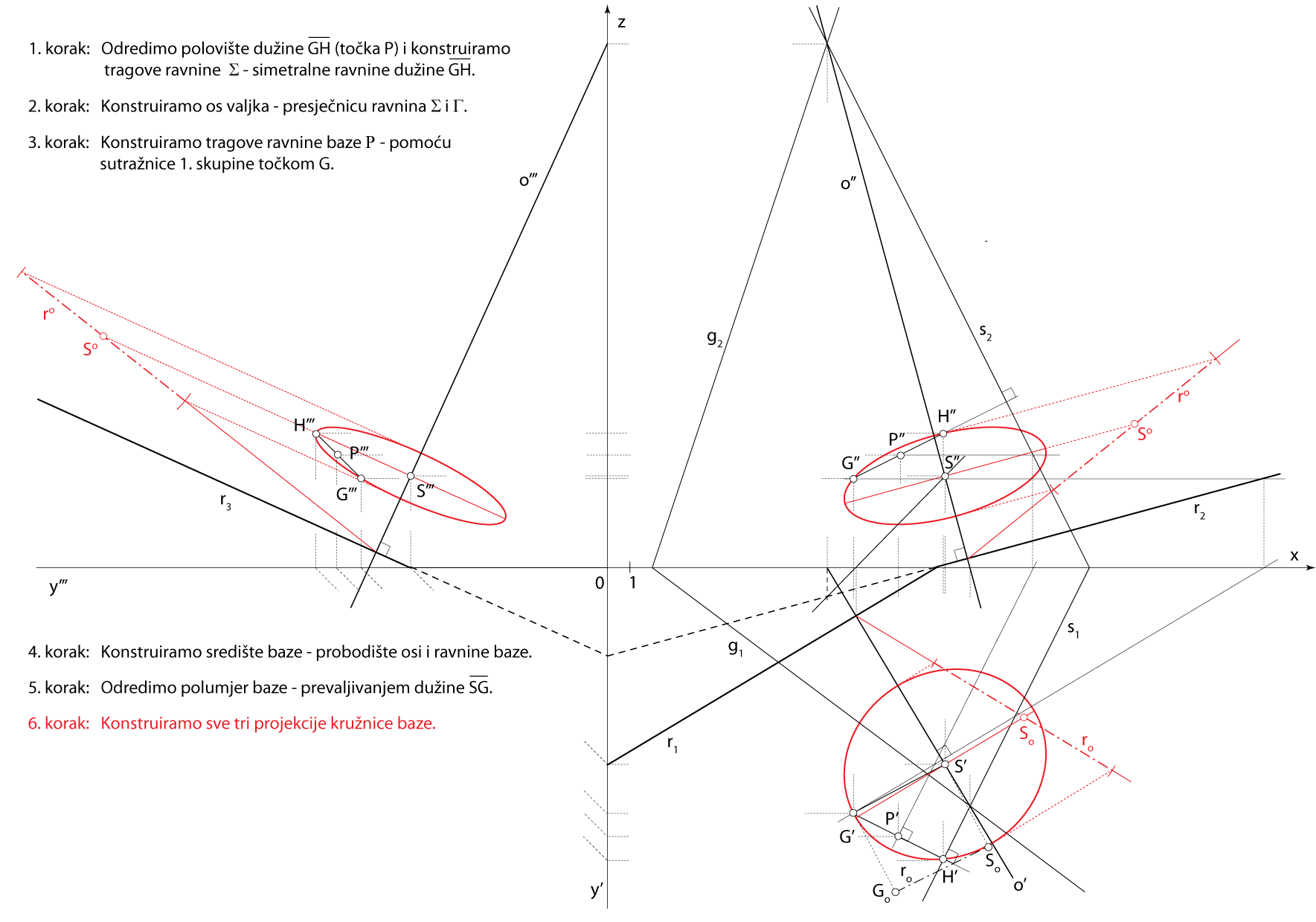
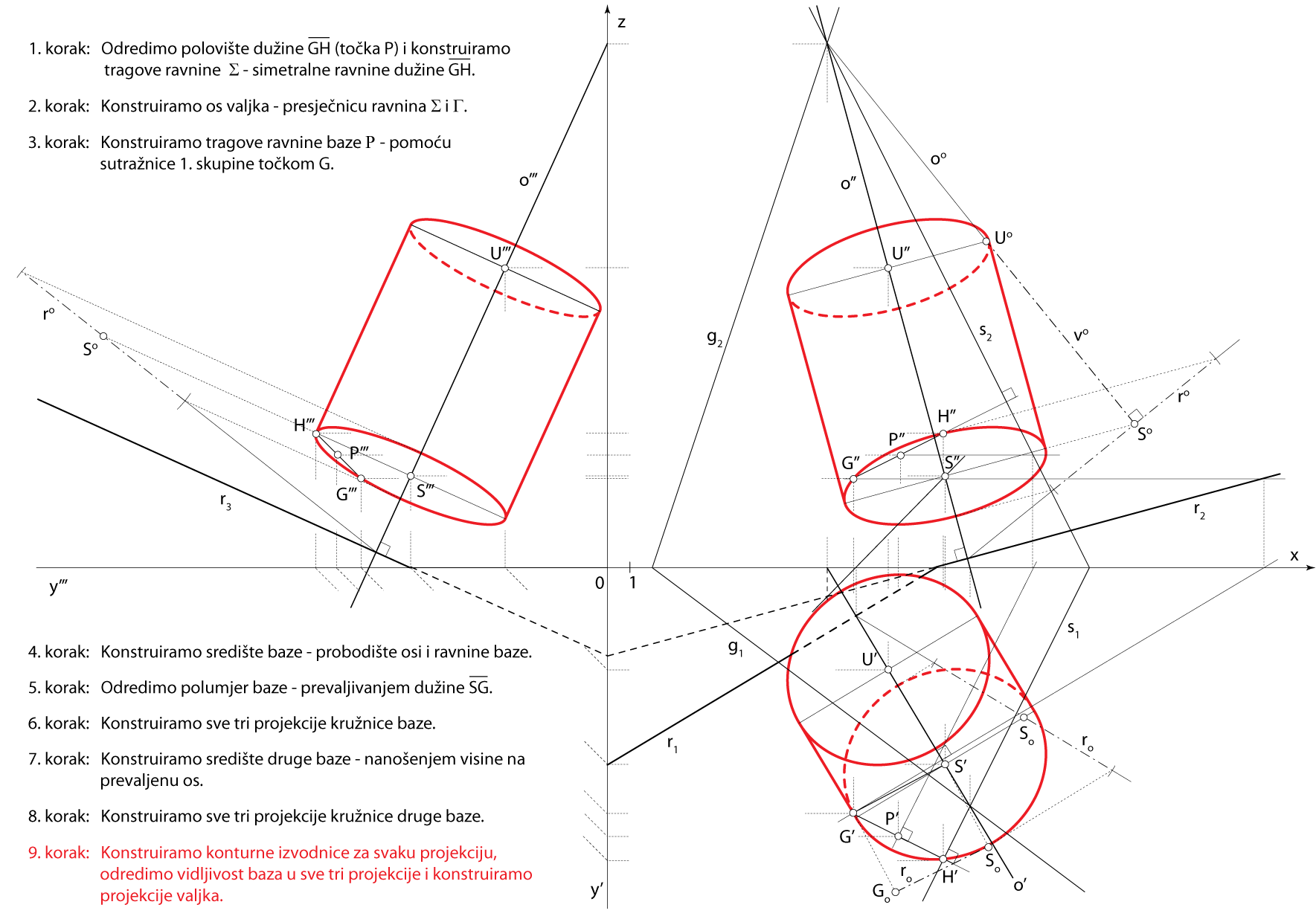
Završni crtež