Neka je \(\small O(x,y,z)\) Kartezijev koordinatni sustav i neka su \(\small X\), \(\small Y\) i \(\small Z\) točke na koordinatnim osima tog sustava (\(\small X \in x\), \(\small Y \in y\), \(\small Z \in z\)) za koje vrijedi \(\small d(O,X) = d(O,Y) = d(O,Z)\), odnosno \(\small O (X, Y, Z)\) je ortonormirani trobrid.

Povežemo li neki prostorni objekt s prikladno odabranim sustavom \(\small O(x,y,z)\) pa ga zajedno s osima tog sustava i jediničnim dužinama na njima paralelno projiciramo na neku ravninu dobit ćemo aksonometrijsku sliku objekta. Postupak takvog projiciranja nazivamo aksonometrijom. Ako je smjer projiciranja nakošen prema ravnini slike (projekcije) postupak nazivamo kosom aksonometrijom.

Prema Pohlkeovom teoremu u ravnini slike možemo odabrati bilo koji ravninski trobrid \(\small \overline O (\overline X, \overline Y, \overline Z)\), odnosno četiri nekolinearne točke, i smatrati ga paralelnom projekcijom ortonormiranog trobrida \(\small O(X, Y, Z)\). Sliku tog prostornog trobrida i njime određenih koordinatnih osi nazivamo osnim križem.

Slika 213: Osni križ
Slika 214: Točka \(\small \overline P\) je aksonometrijska slika točke \(\small P(2,3,2)\)

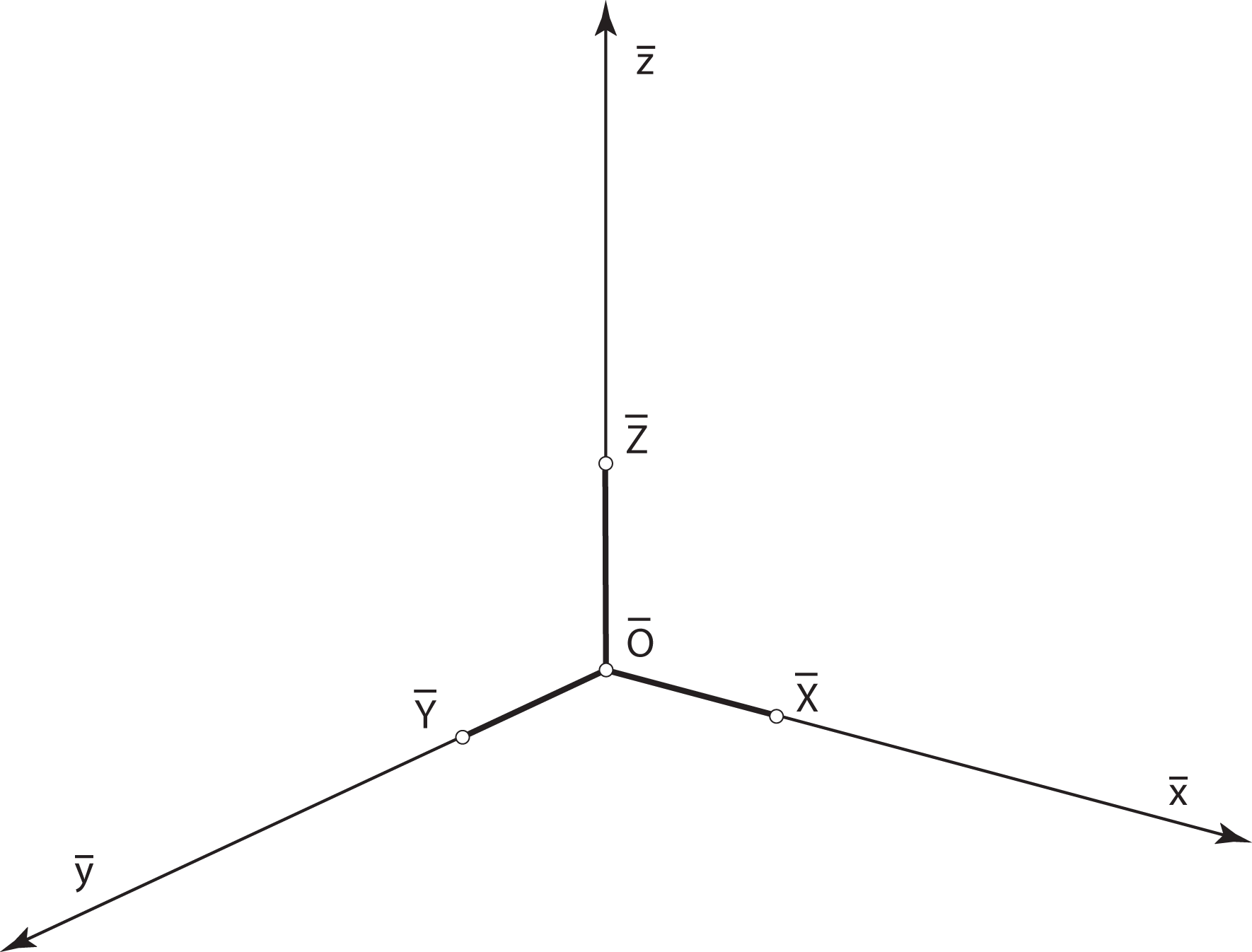
Da bi aksonometrijske slike objekata bile što manje izobličene i da bi što bolje predočavale zadane objekte, u literaturi se ipak preporučuju neka pravila za odabir položaja koordinatnih osi i prikrata\(^*\) u njihovim smjerovima.

Aksonometrijske projekcije koordinatnih osi uobičajeno je postavljati u sljedeći položaj:
  • os \(\small \overline z\) vertikalno
  • osi \(\small \overline x\) i \(\small \overline y\) tako da s horizontalom zatvaraju kutove \(\small \alpha\) i \(\small \beta\), gdje \(\small \alpha\in [10^\circ, 15^\circ]\) i \(\small \beta\in [20^\circ, 30^\circ]\).

Položaj svake točke u prostoru metrički je određen njezinim udaljenostima od koordinatnih ravnina. Udaljenosti se mjere u smjerovima koordinatnih osi \(\small x\), \(\small y\) i \(\small z\). Ako je neka dužina duljine \(\small d\) paralelna s osi \(\small x\), \(\small y\) ili \(\small z\), tada duljinu njezine projekcije redom označavamo \(\small d_x\), \(\small d_y\) ili \(\small d_z\).

  • Brojeve \(\small m=\frac{d_x}{d}\), \(\small n=\frac{d_y}{d}\) i \(\small p=\frac{d_z}{d}\) nazivamo prikratama\(^*\) u smjeru osi, a preporučuju se prikrate \(\small n\leq m\leq p\leq 1\).

\(^*\) Prikrata je omjer duljine projekcije neke dužine i njezine duljine.

Slika 215

Konstrukcija kutova proporcionalnosti

Konstrukcija kutova proporcionalnosti omogućuje da za bilo koje zadane prikrate \(\small m\), \(\small n\), \(\small p\) i neku duljinu \(\small d\), konstruiramo dužine čije su duljine \(\small d_x=m\cdot d\), \(\small \,\, d_y=n\cdot d\), \(\small \,\, d_z=p\cdot d\).

U prezentaciji 41 taj je konstrukcijski postupak izveden za slučaj \(\small m=0.8\), \(\small \,\, n=0.7\), \(\small \,\, p=0.9\). Točnost konstrukcije temelji se na teoremu o sličnosti trokuta.

Vrste aksonometrije prema odnosu prikrata:

  • trimetrija - sve tri prikrate su različite
  • dimetrija - samo su dvije prikrate jednake
  • izometrija\(^*\) - sve su tri prikrate jednake.
\(^*\) U dijelu literature naziv izometrija koristi se za projiciranje kod kojeg su još i sva tri kuta između projekcija osi jednaka.
Prezentacija 41

Pogledi

U našim ćemo primjerima razlikovati dva pogleda zdesna na koordinatne ravnine:

  • pogled odozgo
  • pogled odozdo

Slika 216: Pogled odozgo \(\small -\) oznaka \( \swarrow\)
Slika 217: Pogled odozdo \(\small -\) oznaka \( \nwarrow\)

Primjer 1: Zadana je uspravna šesterostrana piramida kojoj osnovka leži u ravnini \(\small \Pi_1\), točka \(\small S(4,4,0)\) je središte, a točka \(\small A(2,4,0)\) jedan vrh te osnovke. Visina je piramide 4. Konstruirajte projekciju te piramide u kosoj aksonometriji za koju je \(\small (\alpha,\,\beta,\,m,\,n,\,p)=(10^\circ,\,30^\circ,\,0.9,\,0.8,\,1)\). Nacrtajte rješenja za poglede odozgo i odozdo.

Slika 218

Kružnica u kosoj aksonometriji

Zbog svojstava paralelnog projiciranja elipsa je aksonometrijska slika kružnice koja ne leži u projicirajućoj ravnini. Pritom će se svaki par ortogonalnih promjera kružnice projicirati u par konjiguranih promjera elipse koja je njezina projekcija. Za konstrukciju osi elipse koja je zadana parom konjugiranih promjera uobičajeno se koristi Rytzova konstrukcija (Prezentacija 44).

Primjer 2: Dužina \( \small{\overline{ST}[S(0,5,5),T(12,5,5)]}\) os je rotacijskog valjka kojem je polumjer osnovke duljine 2. Konstruirajte projekciju dvostrukog uvećanja tog valjka u kosoj aksonometriji za koju je \(\small (\alpha,\,\beta,\,m,\,n,\,p)=(15^\circ,\,25^\circ,\,0.9,\,0.9,\,1)\). Projekciju objekta prikažite s pogledom odozgo.

Slika 219

Zadatak 1: Konstruirajte kosu aksonometriju objekta čiji su tlocrt i nacrt dani na slici 220. Zadatak riješite u izometriji.

Slika 220
Rješenje: prezentacija 46

Zadatak 2: Konstruirajte kosu aksonometriju uglatog objekta čiji su tlocrt i nacrt dani na slici 221. Zadatak riješite u izometriji.

Slika 221
Rješenje: slika 222