Teorija vjerojatnosti je matematička disciplina čiji je zadatak formirati i proučavati matematički model slučajnog pokusa. U 17. stoljeću, inspirirani kockarskim igramam matematičari B. Pascal i P. Fermat su se prvi bavili vjerojatnosnim problemima.
Pokus (eksperiment) je definiran odnosom uzroka i posljedica. Pretpostavke za
realizaciju pokusa su: ponavljanje pokusa proizvoljno konačno mnogo puta i poznavanje
moguć ih ishoda.
Ishodi pokusa su jedini objekti za izgradnju matematičkog modela pokusa.
U determinističkom pokusu ishod je jednoznačno odreden uvjetima pokusa, a u
slučajnom pokusu ishod nije jednoznačno odeden uvjetima pokusa.
Osnovna pretpostavka slučajnog pokusa je da svako vršenje pokusa mora dati ishod
(dogadaj) koji odgovara jednom i samo jednom elementarnom dogadaju.
MOTIV 2.1 (a) Bacamo igraću kocku. Koji su ishodi slučajnog pokusa?
(b) Bacamo istovremeno dvije igraće kocke. Koji su ishodi slučajnog pokusa?
Definicija 2.1 (ELEMENTARNI DOGAĐAJ.PROSTOR ELEMENTARNIH DOGAĐAJA)
Slučajni pokus je definiran svojim osnovnim ishodima koji se medusobno
isključuju i zovu se elementarni dogadaji. Označavaju se malim grčkim slovima
ω1,ω2,..
Skup Ω = {ωi : ωi =elementarni dogadaji, i = 1,..,n} je neprazan skup i zove se
prostor elementarnih dogadaja.
PRIMJER 2.1
Slučajni pokus= bacanje novčića;
elementarni dogadaji: ω1,ω2; ω1 = ”palo pismo”, ω2 = ”pala glava”;
Prostor elementarnih dogadaja Ω = {ω1,ω2}.
PRIMJER 2.2 motiv
(a) Slučajni pokus= bacanje kocke;
elementarni dogadaji: ω1,...,ω6; ω1 = ”pao broj 1”, .....,omega6 = ”pao broj 6”;
Prostor elementarnih dogadaja Ω = {ω1,...,ω6}
(b) Slučajni pokus= bacanje istovremeno dvije kocke;
elementarni dogadaji: ω1,...,ω36; ω1 = (1,1),... ,ω36 = (6,6).
Prostor elementarnih dogadaja Ω = {ω1,...,ω36}.
PRIMJER 2.3
Slučajni pokus (eksperiment)= vrijeme trajanja tri sijalice;
elementarni dogadaj: ω = (x,y,z) ∈ ℝ3 : x > 0,y > 0,z > 0; Prostor elementarnih
dogadaja Ω = {ω = (x,y,z) ∈ ℝ3 : x > 0,y > 0,z > 0}
PRIMJER 2.4 Slučajni pokus (eksperiment)= dnevna količina padalina i
maksimalna dnevna temperatura u Zagrebu;
elementarni dogadaj: ω = (x,y) : x ≤ 0,-30 < y ≤ 50; Prostor elementarnih
dogadaja Ω = {ω = (x,y) ∈ ℝ2 : x ≤ 0,-30 < y ≤ 50}
Definicija 2.2 (SLUČAJNI DOGAĐAJ)
Slučajni dogada je podskup prostora elementarnih dogadaja . Slučajni dogadaji
označavaju se velikim tiskanim slovima latinice A,B,...; A ⊆ Ω.
(SIGURAN DOGAĐAJ)
Cijeli prostor elementarnih dogadaja Ω je siguran dogadaj koji se mora dogoditi
u svakom vršenju pokusa.
(NEMOGUĆ DOGAĐAJ)
Prazan skup ∅ je nemoguć dogadaj koji se nikad neće dogoditi.
(POVOLJAN DOGAĐAJ)
Elementarni dogadaj koji pripada dogadaju A zove se povoljan za dogadaj A ako pojavljivanje tog elementarnog dogadaja u pokusu povlačda se dogodio dogadaj A.
PRIMJER 2.5
Slučajni pokus=bacanje igraće kocke;
elementarni dogadaji: ω1 = ”pala 1”,..., ω6 = ”pala 6”;
Prostor elementarnih dogadaja: Ω = {ω1,ω2,...,ω6} = {1,2,3,4,5,6};
A=”pao je paran broj”; A={ω2,ω4,ω6} = {2,4,6}.
Elementarni dogadaji ω2,ω4,ω6 su povoljni za dogadaj A.
OPERACIJE SA SKUPOVIMA
Slučajni dogadaji su podskupovi od Ω. Operacije sa dogadajima definiramo pomoću
operacija sa skupovima.
Podskup dogadaja: A ⊆ B : (dogodi se A ⇒ dogodi se B);
Razlika dogadaja: A\B : (dogadaj A\B se dogodi ako se dogodi A i ne dogodi
B);
Suprotan dogadaj: Ac = Ω\A : (Ac se dogodi ⇔ A ne dogodi);
Presjek dogadaja : A ∩ B : (dogadaj A ∩ B se dogodi ⇔ dogode se i A i B);
Unija dogadaja:A ∪ B : (dogadaj A ∪ B se dogodi ⇔ dogodi se ili A ili B);
T: Vrijede de Morganova pravila:
(⋃ kAk)c = ⋂ kAkc;
(⋂ kAk)c = ⋃ kAkc.
Definicija 2.3 (DOGAĐAJI SE ISKLJUČUJU)
Za dogadaje A i B kažemo da se medusobno isključuju ako je njihov presjek jednak ∅ .
Definicija 2.4 (POTPUN SISTEM DOGAĐAJA)
Skupovi A1,A2,...,An čine potpun sistem dogadaja ako se svi medusobno isključuju i ako im je unija cijeli prostor elementarnih dogadaja:
PRIMJER 2.6
Iz skupa jednoznamenkastih brojeva izabiremo jedan broj. Neka je dogadaj
A=”broj je djeljiv s 2” , dogadaj B=”broj je djeljiv s 3”.
Naći izraze za dogadaje C:
(a) C=”broj djeljiv i s 2 i s 3”;
(b) C=”broj djeljiv ili s 2 ili s 3”;
(c) C=”broj paran a nije djeljiv s 3”;
(d) C=”broj nije paran a djeljiv s 3”;
(e) C=”broj nije ni paran ni djeljiv s 3”.
Rješenje: A = {2,4,6,8}, B = {3,6,9}
(a) C=A ∩ B = {6};
(b) C=A ∪ B = {2,3,4,6,8,9};
(c) C=A\B = {2,4,8};
(d) C=B\A = {3,9};
(e) C=(A ∪ B)c = Ac ∩ Bc = {1,5,7}.
PRIMJER 2.7
Iz tablice slučajnih brojeva izabran je jedan broj. Dogadaj A=”broj je djeljiv s
dva”, dogadaj B=”zadnja znamenka je 0”. Što označava dogadaj C:
(a) C=A ∩ B;
(b) C=Ac ∩ B;
(c)C=A ∪ B;
Rješenje:
(a) C=”broj je paran i zadnja znamenka je 0”;
(b) C=∅ nemoguć dogadaj;
(c) C=A =”broj je paran”.
PRIMJER 2.8
Slučajni pokus je gadanje u metu. Pokus se ponavlja 3 puta. Promatraju se
dogadaji A, B, C koji znače pogadanje mete u prvom, drugom i trećem pokušaju.
Pomoću tih dogadaja opisati slijedeće dogadaje:
(a) ”sva tri pogotka”;
(b) ”tri promašaja”;
(c) ”bar jedan pogodak”;
(d) ”bar jedan promašaj”;
(e) ”najviše dva pogotka”;
(f) ”najviše jedan pogodak”;
(g) ”bar dva pogotka”;
(h) ”do trećeg gadanja nije bilo pogodaka”.
Rješenje:
(a) A ∩ B ∩ C;
(b) Ac ∩ Bc ∩ Cc = (A ∪ B ∪ C)c;
(c) A ∪ B ∪ C;
(d) Ac ∪ Bc ∪ Cc = (A ∩ B ∩ C)c;
(e) Ac ∪ (A ∩ Bc) ∪ (A ∩ B ∩ Cc) = Ac ∪ Bc ∪ Cc;=(d)
(f) (Ac ∩ Bc ∩ Cc) ∪ (A ∩ Bc ∩ Cc) ∪ (Ac ∩ Bc ∩ C) ∪ (Ac ∩ B ∩ Cc);
(g) (A ∩ B ∩ C) ∪ (A ∩ B) ∪ (A ∩ C) ∪ (B ∩ C);
(h) Ac ∩ Bc = (A ∪ B)c.
PRIMJER 2.9
Za koje dogadaje vrijedi:
(a) A ∪ B = A;
(b) A ∩ B = A;
(c) A ∩ B = A ∪ B;
(d) A ∩ B = Ac
(e) A ∪ B = Ac.
Rješenje:
(a) B ⊂ A;
(b) A ⊂ B;
(c) A = B;
(d) A = Ω,B = ∅;
(e) A = ∅,B = Ω.
Francuski matematičar P.S. Laplace (1749.-1827.) objavio je 1812. djelo ”Theorie
analitique des probabilities” u kojem uvodi pojam elemntarnih dogadaja i pojam
vjerojatnosti a priori i a posteriori. Vjerojatnost dogadaja a priori odreduje preko
omjera koji ovisi o prirodi dogadaja. Za homogeni novčić prije bacanja može se odrediti
da je vjerojatnost (a priori) da će pasti pismo jednaka 
. Vjerojatnost dogadaja a
posteriori odreduje nakon velikog broja ponavljanja eksperimenta kao omjer broja
pojavljivanja dogadaja i ukupnog broja ponavljanja.
MOTIV 2.2
U skupu od 27 proizvoda 7 je neispravnih. Kolika je vjerojatnost da izaberemo uzorak koji se sastoji od 5 dobrih i 3 neispravna proizvoda?
Definicija 2.5 (KLASIČNA DEFINICIJA VJEROJATNOSTI A PRIORI)
Neka je prostor elementarnih dogadaja konačan skup |Ω| = n, Ω = {ω1,...,ωn}.
Neka su svi elementarni dogadaji jednako mogući. Neka dogadaj A ima m povoljnih
elementarnih dogadaja, A ⊂ Ω,|A| = m.
Vjerojatnost svakog elementarnog dogadaja je P(ω) = 
.
Vjerojatnost dogadaja A definira se kao broj:
T: SVOJSTVA:
(1) P(Ω) = 1,
(2) P(Ac) = 1 - P(A),
(3) P(∅) = 0,
(4) 0 ≤ P(A) ≤ 1,
(5) A ⊂ B ⇒ P(A) ≤ P(B),
(6) A ∩ B = ∅⇒ P(A ∪ B) = P(A) + P(B),
(7) P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
D:
(1) P(Ω) = 
= 1,
(2) P(Ac) = 
= 1 -
= 1 - P(A),
(3) P(∅) = P(Ωc) = (2) = 1 - P(Ω) = (1) = 1 - 1 = 0,
(4) A ⊂ Ω,0 < |A| < n ⇒ 0 < P(A) < 1, prema (1) i (3) ⇒ 0 ≤ P(A) ≤ 1.
(5) |A|≤|B|⇒
≤
⇒ P(A) ≤ P(B),
(6) |A ∪ B| = |A| + |B|⇒
P(A ∪ B) = 
= 
= 
+ 
= P(A) + P(B),
(7) |A ∪ B| = |A| + |B|-|A ∩ B|⇒
P(A∪B) = 
= 
= 
+ 
-
= P(A) + P(B) -P(A∩B).
SLABOSTI:
-restriktivna jer se može primijeniti samo na slučajne pokuse s konačno mnogo elementarnih dogadaja;
-kružna jer se u definiciji vjerojatnosti koristi formulacija ”jednako mogući” tj. ”jednako vjerojatni”.
PRIMJER 2.10
Slučajni pokus: bacanje igraće kocke. Kolika je vjerojatnost (klasična apriori) dogadaja A=”pao broj veći ili jednak 3”?
Rješenje:
Ω = {1,2,3,4,5,6}, n = |Ω| = 6.
A = {3,4,5,6}, |A| = 4.
P(A) = 
= 
= 0.666.
PRIMJER 2.11
U kutiji je pet kuglica: dvije bijele i 3 crne. Iz kutije slučajno izvučemo jednu kuglicu. Kolika je vjerojatnost da će izvučena kuglica biti crna?
Rješenje:
Slučajni pokus: izvlačimo kuglicu iz kutije u kojoj su 2 b i 3 c kuglice;
Ω = {b,b,c,c,c}, n = |Ω| = 5.
A=”kuglica je crna”; A = {c,c,c}, |A| = 3,
P(A) = 
= 
.
PRIMJER 2.12
U kutiji je n olovaka jedne vrste od kojih je nT ispravnih, a nD = n - nT neispravnih. Uzmemo slučajni uzorak od r olovaka. Kolika je vjerojatnost da je medu njima rT ispravnih (0 ≤ rT ≤ r)i rD neispravnih?
Rješenje:
Slučajni pokus: izbor od r elemenata (bez vraćanja) iz skupa koji ima n elemenata
n = nT + nD,r = rT + rD.
Ω = {svi uzorci veličine r iz n-čl. skupa}, |Ω| = 
;
Dogadaj A=”uzorak ima rT ispravnih i rD neispravnih”;
|A| = Broj svih uzoraka veličine r iz n-čl. skupa bez vraćanja koji imaju rT ispravnih i
rD neispravnih:
Koristimo formulu za uzorak bez vraćanja (koristimo teorem o uzastopnom
prebrojavanju i broj kombinacija ri-razreda od ni elemenata).
|A| = CnT(rT) ⋅ Cn
D(rD) = 
⋅
= 
⋅
.
P(A) = 
= 
.
PRIMJER 2.13 motiv
U skupu od 27 proizvoda 7 je neispravnih. Kolika je vjerojatnost da izaberemo uzorak koji se sastoji od 5 dobrih i 3 neispravna proizvoda?
Rješenje:
Slučajni pokus: izbor od r elemenata (bez vraćanja) iz skupa koji ima n elemenata
n = nT + nD,r = rT + rD.
n = 27, r = 8, nT = 20, nD = 7, rT = 5, rD = 3.
Ω ={svi uzorci veličine r = 8 iz n = 27-čl. skupa};
|Ω| = 
= 
= 2220075;
Dogadaj A=”uzorak ima rT = 5 ispravnih i rD =3 neispravnih”;
|A| =Broj svih uzoraka veličine r iz n -čl. skupa bez vraćanja koji imaju rT ispravnih
od nT i rD neispravnih od nD:
|A| = 
⋅
= 
⋅
= 
⋅
= 542640
P(A)=
= 
= 0.24442.
MOTIV 2.3 Kolika je vjerojatnost šestice kod bacanja igraće kocke? Bacili smo kocku 1000 puta i 170 puta je pala šestica.
Definicija 2.6 (KLASIČNA DEFINICIJA VJEROJATNOSTI
A POSTERIORI)
Neka se slučajni pokus ponavlja n puta, n ∈ N, i neka dogadaj A nastupi
nA puta. Ako slučajni pokus zadovoljava uvjet statističke stabilnosti relativnih
frekvencija, tj. limn→∞
= p, onda se vjerojatnost a posteriori dogadaja A
definira kao broj:
Često se P(A) zove STATISTIČKA DEFINICIJA VJEROJATNOSTI.
T: SVOJSTVA:
ω1 = 0 = ”nije se dogodio A”;
ω2 = 1 = ”dogodio se A”;
Ω = {0,1}× ... ×{0,1},n puta;
(1) P(Ω) = limn→∞
= limn→∞
= 1,
(2) P(Ac) = 1 - P(A),
(3) P(∅) = 0,
(4) 0 ≤ P(A) ≤ 1,
(5) A ⊂ B ⇒ P(A) ≤ P(B),
(6) A ∩ B = ∅⇒ P(A ∪ B) = P(A) + P(B),
(7) P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
D: analogno kao klasična definicija vjerojatnosti a priori.
SLABOSTI:
P(A)=limn→∞
,
∀ϵ > 0,∃n0 ∈ N,∀n > n0 ⇒|P(A) -
| < ϵ, ali n0 ovisi o realizaciji slučajnog
pokusa.
Za konkretan slučajni pokus teško provjeriti ima li svojstvo stabilnosti relativnih
frekvencija!
PRIMJER 2.14 motiv
Kolika je vjerojatnost šestice kod bacanja igraće kocke? Bacili smo kocku 1000 puta i 170 puta je pala šestica.
Rješenje: Slučajni pokus: bacanje kocke.
ω1 = 1 = ” pala broj 1”; ω6 = 6 = ”pao broj 6”;
Ω = {1,2,..,6}× ... ×{1,2,..,6},n = 1000 puta;
Pokus zadovoljava uvjet statističke stabilnosti relativnih frekvencija ako jekocka
homogena.
P(ω1)=limn→∞
= p = 
(iskustvo),...,
P(ω6)=limn→∞
= p = 
(iskustvo).
A = ω6, nω6 = 170
P(A) = 
= 
= 0.1705.
PRIMJER 2.15
Bacamo novčić n=24000 puta. Kolika je vjerojatnost a posteriori dogadaja A=”palo pismo” ako je pismo palo 12012 puta.
Rješenje: Slučajni pokus: bacanje novčića.
ω1 = 0 = ”nije palo pismo”; ω2 = 1 = ”palo pismo”;
Ω = {0,1}× ... ×{0,1},n = 24000 puta;
Pokus zadovoljava uvjet statističke stabilnosti relativnih frekvencija ako je
homogen.
P(ω1)=limn→∞
= p = 
(iskustvo),
P(ω2)=limn→∞
= p = 
(iskustvo).
A = ω2, nω2 = 12012
P(A) = 
= 
= 0.5005.
MOTIV 2.4 Mladić i djevojka su dogovorili sastanak na trgu u 12 sati. Čekat će se najdulje 20 minuta nakon dolaska. Kolika je vjerojatnost da se susretnu ako su oboje došli na trg od 12 do 13 sati?
Definicija 2.7 Neka se slučajni pokus sastoji u slučajnom izboru točke u skupu
Ω = Rn za koji vrijedi μ(Ω) > 0, gdje je μ geometrijska mjera (Lebegova mjera) (za
n=1 duljina, n=2 površina, n=3 volumen). Neka je dogadaj A ⊂ Ω izbor točke iz
skupa A (A je Borelov skup). Geometrijska vjerojatnost dogadaja A, (vjerojatnost
da je izabrana točka iz skupa A) je broj P(A) = 
.
PRIMJER 2.16
U kvadratu stranice a slučajno je izabrana jedna točka. Kolika je vjerojatnost da je točka s dijagonale kvadrata?
Rješenje:
Slučajni pokus: slučajni izbor točke u skupu Ω = [0,a] × [0,a].
A=dijagonala kvadrata, A ⊂ Ω, A = {(x,y) ∈ Ω : x = y}.
μ(Ω) = a2, μ(A) = 0, P(A) = 
= 0.
PRIMJER 2.17
U kvadratu stranice a slučajno je izabrana jedna točka. Kolika je vjerojatnost da je točka unutar upisanog kruga?
Rješenje:
Slučajni pokus: slučajni izbor točke u skupu Ω = [0,a] × [0,a].
A=upisani krug u kvadrat, A ⊂ Ω, A = {(x,y) ∈ Ω : x2 + y2 = (
)2}.
μ(Ω) = a2, μ(A) = (
)2π, P(A) = 
= 
= 
.
PRIMJER 2.18
Kolika je vjerojatnost da zbir dva slučajno izabrana broja unutar segmenta [0,1] bude manji od 1, a da njihov produkt bude manji od 2/9?
Rješenje: Ω = [0,1] × [0,1];A ⊂ Ω,
A = {(x,y) ∈ Ω : 0 ≤ x ≤ 1∕3,0 ≤ y ≤ 1 - x}∪
{(x,y) ∈ Ω : 
≤ x ≤ 2∕3,0 ≤ y ≤
}∪
{(x,y) ∈ Ω : 
≤ x ≤ 1,0 ≤ y ≤ 1 - x}.
μ(Ω) = 1, μ(A) = 
+ 
ln2, P(A) = 
= 
+ 
ln2.
PRIMJER 2.19 Na brojevnom pravcu odaberem slučajno točke a i b tako da je a ∈ [0,3],b ∈ [-2,0]. Odredite vjerojatnost da je udaljenost točaka a i b veća od 3?
Rješenje: Ω= točka je unutar pravokutnika [0,3] × [-2,0].
A = točka je unutar trokuta {(x,y) ∈ Ω : x - y > 3,x > 1,y > -2}.
μ(Ω) = 6,μ(A) = 2, P(A) = 
= 
= 
.
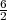PRIMJER 2.20 motiv Mladić i djevojka su se dogovorili sastanak na trgu u 12 sati i čekat će se najdulje 20 minuta nakon dolaska. Kolika je vjerojatnost da se susretnu ako su oboje došli na trg od 12 do 13 sati?
Rješenje: Susret je unutar vremenskog razmaka od 60 minuta pa je Ω = [0,60] × [0,60].
Treba odrediti vjerojatnost dogadaja A=par se susreo={(x,y) ∈ Ω : |x - y| < 20}.
P(A) = 
= 
.
| Prostor elemntarnih dogadaja | Ω = {ω1,...,ωn} |
| Dogadaj A ⊂ Ω | |A| broj povoljnih elem. dog. za A |
| Klasična vjerojatnost a priori | P(A) =  |
| Klasična vjerojatnost a posteriori | P(A) = limn→∞ |
| Geometrijska vjerojatnost | P(A) =  |