PRIMJER 15.2 Neka je nul-hipoteza H0(p = p0) za slučajne varijable koje
imaju B(1,p) binomnu distribuciju.
Test statistika T =  ∑
i=1nX
i ima normalnu distribuciju T ~ N(p,
∑
i=1nX
i ima normalnu distribuciju T ~ N(p, p(1 - p)),
za n →∞.
p(1 - p)),
za n →∞.
Teorija testiranja statističkih hipoteza sastoji se u odredivanju kriterija na osnovu kojeg pomoću eksperimentalnih vrijednosti slučajne varijable možemo odlučiti prihvaćamo li ili odbacujemo hipotezu. Parametarske hipoteze odnose se na parametre poznate funkcije distribucije slučajne varijable, a neparametarske se odnose na nepoznatu razdiobu.
Definicija 15.1 (STATISTIČKA HIPOTEZA)
Statistička hipoteza je bilo koja pretpostavka o distribuciji neke slučajne varijable (slučajnog vektora). Neparametarska hipoteza je pretpostavka o funkciji distribucije neke slučajne varijable. Parametarska hipoteza je pretpostavka o parametrima poznate distribucije neke slučajne varijable. Statističke hipoteze označavamo s H0,H1,..,Hn.
PRIMJER 15.1 H0(λ = λ0) je parametarska hipoteza za parametar λ u Poissonovoj distribuciji.
Definicija 15.2 (PROSTA HIPOTEZA)
Parametarska hipoteza je prosta hipoteza ako sadrži samo jednu pretpostavku
o parametru (npr. H0(μ = μ0)). Parametarska hipoteza je složena ako se sastoji
od konačno ili beskonačno mnogo prostih hipoteza
(npr. H1(μ > μ0), H1(μ < μ0), H1(μ≠μ0)).
Definicija 15.3 (STATISTIČKI TEST)
Testiranje statističkih hipoteza moguće je ako postaje barem dvije alternativne hipoteze: H0 nul-hipoteza i njoj alternativna H1 hipoteza (u nekom smislu suprotna). Statistiku T na uzorku (X1,X2,...,Xn) pomoću koje se donosi odluka o prihvaćanju nul-hipoteze ili prihvaćanju neke od alternativno postavljenih hipoteza ako je dobivena vrijednost slučajnog uzorka (x1,x2,...,xn) zovemo statističkom testom. Test statistika ima svoju poznatu distribuciju.
PRIMJER 15.2 Neka je nul-hipoteza H0(p = p0) za slučajne varijable koje
imaju B(1,p) binomnu distribuciju.
Test statistika T =  ∑
i=1nX
i ima normalnu distribuciju T ~ N(p,
∑
i=1nX
i ima normalnu distribuciju T ~ N(p, p(1 - p)),
za n →∞.
p(1 - p)),
za n →∞.
Definicija 15.4 (GREŠKA PRVE VRSTE, NIVO ZNAČAJNOSTI)
Testom je napravljena greška prve vrste ako se nije prihvatila ispravna
nul-hipoteza.
Vjerojatnost da se napravi greška prve vrste naziva se nivo (razina) značajnosti i
označava s α.
Definicija 15.5 GREŠKA DRUGE VRSTE, JAKOST TESTA
Testom je napravljena greška druge vrste ako se prihvatila lažna nul-hipoteza.
Vjerojatnost da se napravi greška druge vrste označava s β.
Vjerojatnost da se ne napravi greška druge vrste zove se jakost testa označava s
η, η = 1 - β.
(Jakost testa je vjerojatnost da se odbaci lažna nul-hipoteza.)
Definicija 15.6 Kritično područje
Vrijednost tkr statistike T na uzorku (X1,X2,...,Xn) na osnovu koje odlučujemo
prihvacamo li ili odbacujemo nul-hipotezu H0 zove se kritična točka.
Skup vrijednosti statistike T za koje se prihvaća H0 zove se područje prihavćanja
nul-hipoteze, a skup vrijednosti statistike T za koje se ne prihvaća H0 zove se
kritično područje.
Jednostrano kritično područje može biti odredeno s uvjetom T > tkr za tkr > 0 ili
uvjetom T < tkr za tkr < 0.
Dvostrano kritično područje odredeno je s uvjetom T < tkr1 i T > tkr2 za
tkr1 < tkr2.
NAPOMENA 15.1 Neka je zadan nivo značajnosti α i test statistika T za
parametarsku hipotezu H0(parametar = parametar0).
(a) Za dvostrani test:


 , P(T > tkr2) =
, P(T > tkr2) =  ;
;  i tkr2 = z1-
i tkr2 = z1-




NAPOMENA 15.2 Vrijednosti α,β ovise o tkr. Želimo da obe greške budu male
a to je kontradiktorno (ako α opada, tkr se miče u desno i β raste.)
U praksi se na početku izabere α = 0.05 ili α = 0.01, zatim se odredi tkr i na kraju
se izračuna β. Ako je β veliko onda ponavljamo test pomoću većeg uzorka.
NAPOMENA 15.3 Svi teoremi o testiranju hipoteza o parametrima (očekivanje, vjerojatnost i varijanca) su dani bez dokaza. Dokazi se temelje na rezultatima dobivenim u poglavlju Intervali povjerenja i u uvodu objašnjenog postupka.
MOTIV 15.1 Proizvodač lijeka tvdri da je lijek za alergiju djelotvoran 90% u vremenskom razdoblju od 8 sati tako da se ukloni alergijska reakcija kože. Liječnik je vršio istraživanje. Na uzorku od 200 pacijenata s alergijskim problemima lijek je bio učinkovit kod njih 160. Koji je zaključak liječnik dobio- treba li vjerovati deklaraciji proizvodača? Pretpostavimo da je odluku donio uz razinu značajnosti 1% tj. vjerojatnost da je odbacio istinitu tvrdnju je 1%.
TEOREM 15.1 Ako je broj ponavljanja u Bernoullijevoj shemi veliki onda za parametarsku hipotezu H0(p = p0) test statistika


 , tkr2 = z1-
, tkr2 = z1- su kvantili za F*, funkciju distribucije T ~ N(0,1).
su kvantili za F*, funkciju distribucije T ~ N(0,1).
 ∈ (tkr1,tkr2) prihvaćamo nulhipotezu H0, inače prihvaćamo
alternativnu H1.
∈ (tkr1,tkr2) prihvaćamo nulhipotezu H0, inače prihvaćamo
alternativnu H1.
 ∈ (tkr1,∞) prihvaćamo nul-hipotezu H0, inač prihvaćamo alternativnu
H1.
∈ (tkr1,∞) prihvaćamo nul-hipotezu H0, inač prihvaćamo alternativnu
H1.
 ∈ (-∞,tkr) prihvaćamo nul-hipotezu H0, inač prihvaćamo
alternativnu H1.
∈ (-∞,tkr) prihvaćamo nul-hipotezu H0, inač prihvaćamo
alternativnu H1.
PRIMJER 15.3 Napravljen je slučajni pokus bacanje novčića. Pokus je ponovljen n=4040 puta i dobiveno je 2048 grbova. Znamo da je uspjeh u pokusu binomna slučajna varijabla s parametrom p vjerojatnost da padne grb. Testiramo nulhipotezu H0(p = 0.5) tj. testiramo hipotezu da je novčić ispravan. Alternativna hipozeza je H1(p≠0.5). Neka je nivo značajnosti α = 0.05.
Rješenje: Postavljamo hipoteze:
nul-hipoteza H0(p = 0.5)
alternativna hipoteze H1(p≠0.5) H1(p < 0.5) i H1(p > 0.5).
Za zadani α = 0.05 provjeravamo dvostrani test.
tkr1 = z0.025, tkr2 = z0.975 su kvantili standardne normalne distribucije F*.

Područje prihvaćanja za nul-hipotezu H0(p = 0.5) za nivo značajnosti
α = 0.05 je (tkr1,tkr2) = (-1.96,1.96).
Vrijednost test statistike T(X1,X2,...,Xn), je

PRIMJER 15.4 motiv
Proizvodač lijeka tvdri da je lijek za alergiju djelotvoran 90% u vremenskom razdoblju od 8 sati tako da se ukloni alergijska reakcija kože. Liječnik je vršio istraživanje. Na uzorku od 200 pacijenata s alergijskim problemima lijek je bio učinkovit kod njih 160. Koji je zaključak liječnik dobio- treba li vjerovati deklaraciji proizvodača? Pretpostavimo da je odluku donio uz razinu značajnosti 1% tj. vjerojatnost da je odbacio istinitu tvrdnju je 1%.
Rješenje: Postavljamo hipoteze:
H0(p = 0.9), deklaracija o lijeku je isprvna
H1(p < 0.9) deklaracija je lažna.
U zadatku je zadano α = 0.01, p0 = 0.9, x =  , n = 200.
, n = 200.
Test statistika je T = 
 i ima standardnu normalnu distribuciju
T ~ N(0,1), n →∞.
i ima standardnu normalnu distribuciju
T ~ N(0,1), n →∞.
Za jednostrani test, kritičnu točku tkr odredujemo iz uvjeta P(T < tkr) = α. Tako je
tkr = zα kvantili za F*, funkciju distribucije T ~ N(0,1).
Kritična točka je tkr = zα = -z1-α = -2.33.
Područje prihvaćanja za nul-hipotezu H0(p = 0.9) za nivo značajnosti
α = 0.01 je (tkr,∞) = (-2.33,∞).
Vrijednost test statistike T(X1,X2,...,Xn),

 (tkr,∞) nije unutar područja prihvatljivosti nul-hipoteze, prihvaćamo
alternativnu H1(p < 0.9) tj. deklaracija nije vjerodostojna uz razinu značajnosti
1%.
(tkr,∞) nije unutar područja prihvatljivosti nul-hipoteze, prihvaćamo
alternativnu H1(p < 0.9) tj. deklaracija nije vjerodostojna uz razinu značajnosti
1%.
(i za n > 30 )
MOTIV 15.2
Prekidna čvrstoća kablova proizvedenih u jednoj tvornici ima uzoračku aritmetičku sredinu 815 kg i standardnu devijaciju 45 kg. Novom tehnologijom u proizvodnom procesu tvrdi se da je prekidna čvrstoća povećana. Da testira tu tvrdnju kontrolor je testirao 50 kablova i dobio uzoračku aritmetičku sredinu 840 kg. Hoće li kontorlor prihvatiti tvrdnju proizvodača uz razinu značajnosti 1%.
U 13. i 14. poglavlju (Intervali povjerenja) uočili smo da pomoću statistika
T(X1,...,Xn) donosimo zaključke o parametrima teorijske distribucije (očekivanje μ i
varijanca σ2). U slučaju velikog uzorka sve statsitike imaju normalnu distribuciju
N(μ, ) bez obzira o teorijsku distribuciju populacije. Zato, za velike uzorke, ako nije
poznata varijanca, možemo korigiranu uzoračku varijancu
) bez obzira o teorijsku distribuciju populacije. Zato, za velike uzorke, ako nije
poznata varijanca, možemo korigiranu uzoračku varijancu  2 i uzoračku varijancu
2 i uzoračku varijancu  2
uzeti za procjenu σ2.
2
uzeti za procjenu σ2.
TEOREM 15.2 Neka je (X1,X2,..Xn) slučajni uzorak slučajne varijable X
koja ima poznatu distribuciju (normalna) s nepoznatim parametrom očekivanje μ
i poznatom varijancom σ2 (ili poznatom korigiranom uzoračkom varijancom  2).
Ako je veliki uzorak (n →∞) za parametarsku hipotezu H0(μ = μ0) test statistika
T =
2).
Ako je veliki uzorak (n →∞) za parametarsku hipotezu H0(μ = μ0) test statistika
T = 
 ima standardnu normalnu distribuciju T ~ N(0,1).
ima standardnu normalnu distribuciju T ~ N(0,1).
Neka je zadan nivo (razina) značajnosti α.
(a) Za dvostrani test:
nul-hipoteza H0(μ = μ0) i alternativna H1(μ≠μ0),
kritične točke tkr1, tkr2, odredujemo iz uvjeta

 , tkr2 = z1-
, tkr2 = z1- su kvantili za F*, funkciju distribucije T ~ N(0,1).
su kvantili za F*, funkciju distribucije T ~ N(0,1).
 ∈ (tkr1,tkr2) prihvaćamo nulhipotezu H0, inače prihvaćamo alternativnu
H1.
∈ (tkr1,tkr2) prihvaćamo nulhipotezu H0, inače prihvaćamo alternativnu
H1.
 ∈ (tkr,∞) prihvaćamo nul-hipotezu H0, inače prihvaćamo alternativnu
H1.
∈ (tkr,∞) prihvaćamo nul-hipotezu H0, inače prihvaćamo alternativnu
H1.
 ∈ (-∞,tkr) prihvaćamo nul-hipotezu H0, inače prihvaćamo alternativnu
H1.
∈ (-∞,tkr) prihvaćamo nul-hipotezu H0, inače prihvaćamo alternativnu
H1.
PRIMJER 15.5 Slučajna varijabla X ~ N(μ,σ2 = 4). U uzorku veličine n=25
vrijednost uzoračke aritmetičke sredine je x = 14.7. Za nivo značajnosti α = 0.01
testirati
(a) nul-hipotezu H0(μ = 16) i alternativnu hipotezu H1(μ≠16),
(b) nul-hipotezu H0(μ = 16) i alternativnu hipotezu H1(μ < 16).
Rješenje :
Zadan je uzorak iz normalne distribucije pa za parametarsku hipotezu H0(μ = μ0) test
statistika T = 
 ima standardnu normalnu distribuciju T ~ N(0,1).
ima standardnu normalnu distribuciju T ~ N(0,1).
Nivo značajnosti je α = 0.01, i n = 25.
(a)Testiramo:
nul-hipotezu H0(μ = 16) i alternativnu hipotezu H1(μ≠16),
Kritične točke su kvantili za F* :



 =
= 
 = -3.25
= -3.25 (tkr1,tkr2) pa odbacujemo nul-hipotezu H0(μ = 16)
i prihvaćamo alternativnu hipotezu H1(μ≠16).
(tkr1,tkr2) pa odbacujemo nul-hipotezu H0(μ = 16)
i prihvaćamo alternativnu hipotezu H1(μ≠16).
 =
=  ⋅
⋅ = -3.,25
= -3.,25 (-2.33,∞), pa odbacujemo nul-hipotezu i
prihvaćamo alternativnu hipotezu H1(μ < 16).
(-2.33,∞), pa odbacujemo nul-hipotezu i
prihvaćamo alternativnu hipotezu H1(μ < 16).
PRIMJER 15.6 motiv
Prekidna čvrstoća kablova proizvedenih u jednoj tvornici ima uzoračku aritmetičku sredinu 815 kg i standardnu devijaciju 45 kg. Novom tehnologijom u proizvodnom procesu tvrdi se da je prekidna čvrstoća povećana. Da testira tu tvrdnju kontrolor je testirao 50 kablova i dobio uzoračku aritmetičku sredinu 840 kg. Hoće li kontorlor prihvatiti tvrdnju proizvodača uz razinu značajnosti 1%.
Rješenje :
Uzorak je veliki n > 30, pa za parametarsku hipotezu H0(μ = μ0) test statistika
T = 
 ima standardnu normalnu distribuciju T ~ N(0,1).
ima standardnu normalnu distribuciju T ~ N(0,1).
Testiramo:
nul-hipoteza H0(μ = 815) i alternativna H1(μ > 815)
pomoću jednostranog testa.
U zadatku su poznati podatci n = 50, = 45,x = 840,α = 0.01.
= 45,x = 840,α = 0.01.
Za veliki uzorak standardnu devijaciju σ procijenit ćemo sa uzoračkom devijacijom  .
Za jednostrani test, kritičnu točku tkr odredujemo iz uvjeta P(T > tkr) = α;
.
Za jednostrani test, kritičnu točku tkr odredujemo iz uvjeta P(T > tkr) = α;
tkr = z1-α = 2.33 je kvantil standardne normalne distribucije.
Područje prihvaćanja za nul-hipotezu H0(μ = 815) za nivo značajnosti 0.01 je
(-∞,2.33).
Vrijednost test statistike T(X1,X2,...,Xn),
t = 
 =
= 
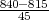 = 3.93
= 3.93 (-∞,2.33) pa odbacujemo nul-hipotezu i
prihvaćamo alternativnu hipotezu H1(μ > 815. Kontrolor će prihvatiti tvrdnju
proizvodača o poboljšanju prekidne čvrstoće.
(-∞,2.33) pa odbacujemo nul-hipotezu i
prihvaćamo alternativnu hipotezu H1(μ > 815. Kontrolor će prihvatiti tvrdnju
proizvodača o poboljšanju prekidne čvrstoće.
MOTIV 15.3
Da testira prekidnu čvrstoću užadi kontrolor je testirao 6 užadi i dobio uzoračku aritmetičku sredinu 3515 kg i korigiranu uzoračku varijancu 66 kg. Proizvodač tvrdi da je 3630 kg. Hoće li kontorlor prihvatiti tvrdnju proizvodača uz razinu značajnosti 1%.
MOTIV 15.4
Izvršena su mjerenja tlačne čvrstoće [ ] uzorka betona visoke kvalitete (A)
i običnog betona (B). Dobiveni su sljedeće vrijednosti
] uzorka betona visoke kvalitete (A)
i običnog betona (B). Dobiveni su sljedeće vrijednosti
| A | 357 356 413 |
| B | 346 358 302 |
Pretpostavimo da su tlačne čvrstoće normalno distribuirane i da imaju jednake varijance. Testirajte hipotezu da je oba tipa betona imaju jednaka očekivanja μ1 = μ2 uz alternativnu hipotezu da je μ1 > μ2, uz razinu značajnosti 5%.
TEOREM 15.3 Neka je (X1,X2,..Xn) slučajni uzorak slučajne varijable X koja ima normalnu distribuciju s nepoznatim parametrom očekivanje μ i nepoznatom varijancom σ2. Za parametarsku hipotezu H0(μ = μ0) test statistika


 , tkr2 = z1-
, tkr2 = z1- su kvantili za F, funkciju distribucije T ~ t(n - 1).
su kvantili za F, funkciju distribucije T ~ t(n - 1).
 ∈ (tkr1,tkr2) prihvaćamo nulhipotezu H0, inače prihvaćamo alternativnu
H1.
∈ (tkr1,tkr2) prihvaćamo nulhipotezu H0, inače prihvaćamo alternativnu
H1.
 ∈ (tkr,∞) prihvaćamo H0, inače prihvaćamo alternativnu H1.
∈ (tkr,∞) prihvaćamo H0, inače prihvaćamo alternativnu H1.
 ∈ (-∞,tkr) prihvaćamo nulhipotezu H0, inače prihvaćamo alternativnu
H1.
∈ (-∞,tkr) prihvaćamo nulhipotezu H0, inače prihvaćamo alternativnu
H1.
NAPOMENA 15.4 Kvantili za Studentovu distribuciju za n = 5, t(4),
F(zα) = α :

PRIMJER 15.7 Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznate varijance σ2. Uzet je utorak veličine n = 5 i dobivena je
vrijednost uzoračke aritmetičke sredine x = 10.2, i vrijednost korigirane uzoračke
varijance  2 = 0.64. Za nivo značajnosti α = 0.05 testirati
2 = 0.64. Za nivo značajnosti α = 0.05 testirati
(a) nul-hipotezu H0(μ = 10) i alternativnu hipotezu H1(μ≠10),
(b) nul-hipotezu H0(μ = 10) i alternativnu hipotezu H1(μ < 10).
Rješenje:
Za parametarsku hipotezu H0(μ = μ0) test statistika




 =
=  ⋅
⋅ = 0.55902 ∈ (tkr1,tkr2) je upala u područje prihvaćanja, pa
prihvaćamo nulhipotezu H0(μ = 10).
= 0.55902 ∈ (tkr1,tkr2) je upala u područje prihvaćanja, pa
prihvaćamo nulhipotezu H0(μ = 10).

 =
=  ⋅
⋅ = 0.559 ∈ (-2.13,∞) pa prihvaćamo nul-hipotezu
H0(μ = 10).
= 0.559 ∈ (-2.13,∞) pa prihvaćamo nul-hipotezu
H0(μ = 10).
PRIMJER 15.8 motiv
Da testira prekidnu čvrstoću užadi kontrolor je testirao 6 užadi i dobio uzoračku aritmetičku sredinu 3515 kg i uzoračku standardnu devijaciju 66 kg. Proizvodač tvrdi da je 3630 kg. Hoće li kontorlor prihvatiti tvrdnju proizvodača uz razinu značajnosti 1%.
Rješenje:
Testira se:
nulhipoteza H0(μ = 3630) i alternativna H1(μ < 3630)
pomoću jednostranog testa.
Test statistika T = 
 =
= 
 ima studentovu distribuciju
T ~ t(n - 1).
ima studentovu distribuciju
T ~ t(n - 1).
Za jednostrani test kritičnu točku tkr odredujemo iz uvjeta P(T < tkr) = α.
tkr = zα, je kvantil za F, funkciju distribucije test statistike T ~ t(n - 1).
Za α = 0.01 i n = 6, tkr = zα = z0.01, -tkr = z0.99, -tkr = 3.37, tkr = -3.37.
Područje prihvaćanja za nul-hipotezu H0(μ = 3630) za nivo značajnosti α = 0.01 je
(-3.37,∞).
Vrijednost test statistike T(X1,X2,...,Xn),
t = 
 =
=  ⋅
⋅ = -3.89
= -3.89 (-3.37,∞) pa ne prihvaćamo nulhipotezu
H0(μ = 3630), nego alternativnu H1(μ < 3630). Kontrolor će odbaciti tvrdnju
proizvodača s razinom značajnosti 1%.
(-3.37,∞) pa ne prihvaćamo nulhipotezu
H0(μ = 3630), nego alternativnu H1(μ < 3630). Kontrolor će odbaciti tvrdnju
proizvodača s razinom značajnosti 1%.
NAPOMENA 15.5 Neka su (X1,X2,....Xn) i (Y 1,Y 2,...,Y n) zadana dva
slučajna uzorka iz normalne distribucije nepoznatih očekivanja μ1 i μ2 ali jedankih
varijanci σ12 = σ22. Ako testiramo H0(μ1 = μ2)
uz alternativne hipoteze H1(μ1 > μ2) ili H1(μ1 < mu2) ili H1(μ1≠μ2)
definiramo μ = μ1 - μ2 i testiramo H0 : μ = 0
uz alternativne hipoteze H1(μ > 0) ili H1(μ < 0) ili H1(μ≠0).
PRIMJER 15.9 motiv
Izvršena su mjerenja tlačne čvrstoće [ ] uzorka betona visoke kvalitete (A)
i običnog betona (B). Dobiveni su sljedeće vrijednosti
] uzorka betona visoke kvalitete (A)
i običnog betona (B). Dobiveni su sljedeće vrijednosti
| A | 357 359 413 |
| B | 346 358 302 |
Pretpostavimo da su tlačne čvrstoće normalno distribuirane i da imaju jednake varijance. Testirajte hipotezu da je oba tipa betona imaju jednaka očekivanja μ1 = μ2 uz alternativnu hipotezu da je μ1 > μ2, uz razinu značajnosti 5%.
Rješenje:
Definiramo novu varijablu razlike čvrstoća D i uzorak razlike čvrstoća
| A-B | 11 1 111 |
Uzoračaka aritmetička sredina za D je d = 41, a korigiranqauzoračka varijanca
 D2 = 3700
D2 = 3700
Za ovaj uzorak testiramo nul-hipotezu H0(μ = 0)
uz alternativnu hipotezu H1(μ > 0). Koristimo test statistiku T = 
 koja ima
studentovu distribuciju T ~ t(n - 1).
koja ima
studentovu distribuciju T ~ t(n - 1).
Za jednostrani test, kritičnu točku tkr odredujemo iz uvjeta P(T > tkr) = α.
tkr = z1-α, je kvantil za F, funkciju distribucije test statistike T ~ t(n - 1).
U zadatku je zadana razina značajnosti α = 0.05 i n = 3 pa iz tablice t(2) očitavamo
tkr = z1-α = 2.92.
Područje prihvaćanja za nul-hipotezu H0(μ = 0) za nivo značajnosti α = 0.05 je
(-∞,2.92).
Ako je vrijednost test statistike t = 
 ∈ (tkr,∞) prihvaćamo nul-hipotezu, inače
prihvaćamo alternativnu.
∈ (tkr,∞) prihvaćamo nul-hipotezu, inače
prihvaćamo alternativnu.
t = 
 = 1.167 ∈ (-∞,2.92), pa prihvaćamo nul-hiptezu H0 : μ = 0, tj.
nul-hipotezu H0(μ1 = μ2).
= 1.167 ∈ (-∞,2.92), pa prihvaćamo nul-hiptezu H0 : μ = 0, tj.
nul-hipotezu H0(μ1 = μ2).
S razinom značajnosti 5% prihvaćamo hipotezu da oba betona imaju jednaka očekivanja čvrstoće.
MOTIV 15.5 Očekivana masa palete opeka je 1166.4 kg. Standardna devijacija mase palete opeka je 5.5 kg. Kontrolor je testirao uzorak od 20 paleta i dobio uzoračku standardnu devijaciju 6.5 kg. Može li kontrolor zaključiti da je standardna devijacija u porastu uz nivo značajnosti 5%?
TEOREM 15.4 Neka je (X1,X2,..Xn) slučajni uzorak slučajne varijable X koja ima normalnu distribuciju s nepoznatim parametrom varijancom σ2. Za parametarsku hipotezu H0(σ2 = σ02) test statistika


 , tkr2 = z1-
, tkr2 = z1- su kvantili za funkciju distribucije χ2(n - 1).
su kvantili za funkciju distribucije χ2(n - 1).
 2 ∈ (tkr1,tkr2)
2 ∈ (tkr1,tkr2)
 2 ∈ (tkr,∞)
2 ∈ (tkr,∞)
 2 ∈ (-∞,tkr)
2 ∈ (-∞,tkr)
NAPOMENA 15.6 Kvantili za hikvadrat distribuciju za n = 4, χ2(4),
F(zα) = α :

PRIMJER 15.10 Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2). U uzorku veličine n = 5 vrijednost korigirane uzoračke varijance je
 2 = 0.64 Za nivo značajnosti α = 0.05 testirati
2 = 0.64 Za nivo značajnosti α = 0.05 testirati
(a) nul-hipotezu H0(σ2 = 0.82) i alternativnu hipotezu H1(σ2≠0.8),
(b) nul-hipotezu H0(σ2 = 0.82) i alternativnu hipotezu H1(σ2 < 0.8).
Rješenje :
Za parametarsku hipotezu H0(σ2 = σ02) test statistika

(a) Testitamo:
nul-hipotezu H0(σ2 = 0.82) i alternativnu hipotezu H1(σ2≠0.82),
Za α = 0.05, n = 5 kritične točke su kvantili distribucije χ2(4) :



 2 =
2 =  0.64 = 4 ∈ (0.48,11.14) pa prihvaćamo nul-hipotezu H0.
0.64 = 4 ∈ (0.48,11.14) pa prihvaćamo nul-hipotezu H0. Za α = 0.05, n = 5, kritična točka je kvantil distribucije χ2(4) :
tkr = zα = z0.05,tkr = 0.71.
Područje prihvaćanja za nul-hipotezu H0(σ2 = 0.64) za nivo značajnosti α = 0.05 je
(tkr,∞) = (0.71,∞).
Vrijednost test statistike T(X1,X2,...,Xn),
t = 
 2 =
2 =  0.64 = 4 ∈ (0.71,∞) pa prihvaćamo nul-hipotezu H0(σ2 = 0.64).
0.64 = 4 ∈ (0.71,∞) pa prihvaćamo nul-hipotezu H0(σ2 = 0.64).
PRIMJER 15.11 motiv
Očekivana masa palete opeka je 1166.4 kg. Standardna devijacija mase palete opeka je 5.5 kg. Kontrolor je testirao uzorak od 20 paleta i dobio uzoračku standardnu devijaciju 6.5 kg. Može li kontrolor zaključiti da je standardna devijacija u porastu uz nivo značajnosti 1%?
Rješenje :
U zadatku su zadani n = 20,  = 6.5, i nivo značajnosti α = 0.01.
= 6.5, i nivo značajnosti α = 0.01.
Ako se testira:
nulhipoteza H0(σ = 5.5) i alternativna H1(σ > 5.5),
pomoću jednostranog testa, izabiremo test statistiku


 2 =
2 =  ⋅ 6.52 = 34.35 ∈ (-∞,36.19), pa prihvaćamo o nul-hipotezu
H0(σ = 5.5).
⋅ 6.52 = 34.35 ∈ (-∞,36.19), pa prihvaćamo o nul-hipotezu
H0(σ = 5.5).
TEST HIPOTEZA za parametar t
| slučajni uzorak | (X1,X2,...,Xn) |
| parametar | t |
| nivo (razina) značajnosti | α = 0.01 ili 0.05 |
| nul-hipoteza | H0(t = t0) |
| alternativna hipoteze | H0(t≠t0), H0(t < t0) ,H0(t > t0) |
| test statistika | T uz H0 |
| dvostrani test za t | P(T < tkr1) + P(T > tkr2) = α |
tkr1 = z tkr2 = z1- tkr2 = z1- |
|
| prihvat za H0 | t ∈ (tkr1,tkr2) |
| jednostrani test za t | P(T < tkr) = α |
| tkr = zα | |
| prihvat za H0 | t ∈ (tkr,∞) |
| jednostrani test za t | P(T > tkr) = α |
| tkr = z1-α | |
| prihvat za H0 | t ∈ (-∞,tkr) |
TEST HIPOTEZA za p (n > 30)
| slučajni uzorak | (X1,X2,...,Xn) n > 30 B(n,p) |
| parametar p, | |
| nivo (razina) značajnosti | α = 0.01 ili 0.05 |
| nul-hipoteza | H0(p = p0) |
| alternativna hipoteze | H0(p≠p0), H0(p < p0) ,H0(p > p0) |
| test statistika | T =   ~ N(0,1) ~ N(0,1) |
TEST HIPOTEZA za μ (n > 30)
| slučajni uzorak | (X1,X2,...,Xn) n > 30 iliN(μ,σ2) |
| parametar μ, | σ2 poznat |
| nivo (razina) značajnosti | α = 0.01 ili 0.05 |
| nul-hipoteza | H0(μ = μ0) |
| alternativna hipoteze | H0(μ≠μ0), H0(μ < μ0) ,H0(μ > μ0) |
| test statistika | T =   ~ N(0,1) ~ N(0,1) |
TEST HIPOTEZA za μ (normalne distribucije)
| slučajni uzorak | (X1,X2,...,Xn) n < 30 ili N(μ,σ2) |
| parametar μ, | σ2 nepoznat |
| nivo (razina) značajnosti | α = 0.01 ili 0.05 |
| nul-hipoteza | H0(μ = μ0) |
| alternativna hipoteze | H0(μ≠μ0), H0(μ < μ0) ,H0(μ > μ0) |
| test statistika | T =   ~ t(n - 1) ~ t(n - 1) |
TEST HIPOTEZA za σ2
| slučajni uzorak | (X1,X2,...,Xn) n < 30 ili N(μ,σ2) |
| parametar σ2, | |
| nivo (razina) značajnosti | α = 0.01 ili 0.05 |
| nul-hipoteza | H0(σ2 = σ02) |
| alternativna hipoteze | H0(σ2≠σ02), H0(σ2 < _0) ,H0(σ2 > σ02) |
| test statistika | T =    2 ~ χ2(n - 1) 2 ~ χ2(n - 1) |