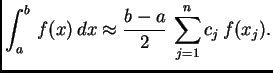 |
(3.23) |
Trapezna i Simpsonova formula su koristile ekvidistantnu podjelu. Točke podjele su bile jednoliko razmještene na segmentu. Te formule u pravilu računaju točno integrale polinoma najviše onog stupnja kojeg je bio interpolacioni polinom. Tako trapezna formula računa točno integrale polinoma do uključivo prvog stupnja.
Postavlja se pitanje da li postoje formule koje računaju točno integrale polinoma stupnja višeg nego što je interpolacioni polinom. Takve formule postoje i zovu se Gaussove kvadraturne formule. U tim formulama točke podjele nisu više ekvidistantno raspoređene. Točke podjele ćemo u daljnjem zvati čvorovima.
Kvadraturna formula općenito je oblika
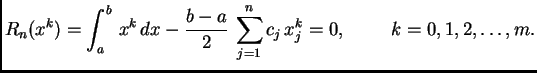
Umjesto rješavanja gornjeg sustava, za određivanje čvorova
![]() i težina
i težina
![]() koristimo ideju
koja potječe od C. F. Gaussa, a osniva se na sljedećem
razmatranju.
koristimo ideju
koja potječe od C. F. Gaussa, a osniva se na sljedećem
razmatranju.
Neprekidne funkcije na ![]() čine vektorski prostor obzirom na
uobičajene operacije zbrajanja funkcija i množenja funkcije
brojem. Svakom paru
čine vektorski prostor obzirom na
uobičajene operacije zbrajanja funkcija i množenja funkcije
brojem. Svakom paru ![]() takvih funkcija možemo pridružiti broj
takvih funkcija možemo pridružiti broj
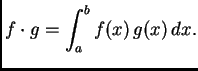
Vratimo se sada na naš problem. Da diskusija ne bi ovisila o
području integracije, prijeđimo na segment ![]() supstitucijom
supstitucijom

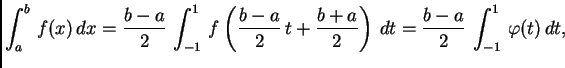
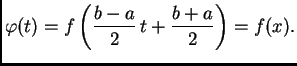
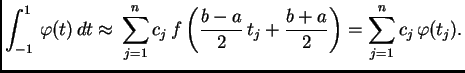
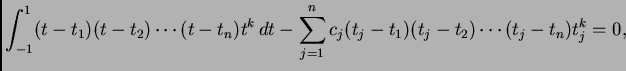
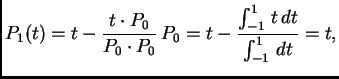
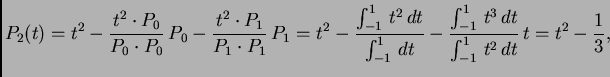
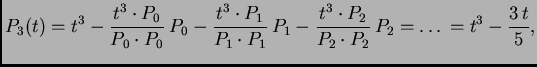
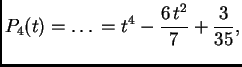
Tako na segmentu ![]() imamo točke kvadrature
imamo točke kvadrature
| 0 | ||||
| 0 | ||||
Težine ![]() jednostavno možemo izračunati na sljedeći
način. Gaussova kvadratura računa točno polinome do uključivo
jednostavno možemo izračunati na sljedeći
način. Gaussova kvadratura računa točno polinome do uključivo
![]() -og stupnja. Neka su
-og stupnja. Neka su
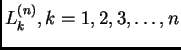 polinomi sa
svojstvom
polinomi sa
svojstvom
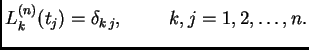
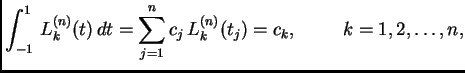
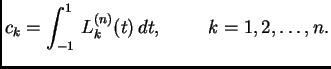
Nultočke Legendreovihovih polinoma uglavnom su iracionalni brojevi, pa uzimajući vrijednosti iz gornje tablice, činimo grešku zamjenjujući iracionalan broj decimalnim. Tako ipak ne dobivamo apsolutnu točnost. No, barem smo uklonili grešku koja se odnosi na zamjenu integrala kvadraturnom formulom.