Osnovne oznake i pojmovi vezani uz perspektivu su:
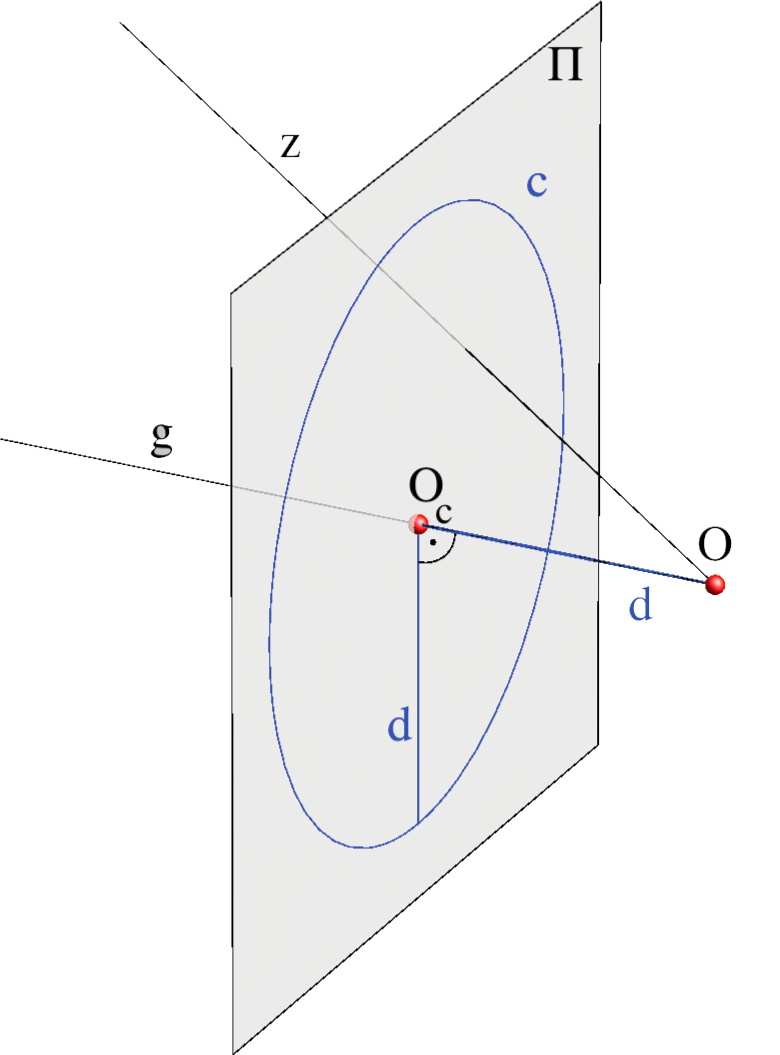
\({\small \Pi}\) \(-\) ravnina projekcije ili ravnina slike (vertikalni položaj)
\({\small O}\) \(-\) centar projekcije ili očište
\({\small z }\) \(-\) zrake projiciranja ili vidni pravci (snop pravaca kroz \({\small O}\))
\({\small g }\) \(-\) glavna zraka ili os pogleda (vidni pravac okomit na \({\small \Pi}\))
\({\small O_c }\)\(-\) glavna točka (ortogonalna projekcija očišta na ravninu slike)
\({\small d }\) \(-\) distancija (udaljenost očišta od ravnine slike)
\({\small c }\) \(-\) distancijska kružnica (kružnica sa središtem \({\small O_c }\) i polumjerom \({\small d}\))

Perspektivnu sliku točke \( {\small T}\) označavat ćemo \({\small T_c}\). Ta je točka probodište vidnog pravca (zrake) kroz točku \( {\small T}\) i ravnine projekcije \( {\small \Pi}\).
Zrake projiciranja koje su paralelne s ravninom slike leže u ravnini koja prolazi točkom \( {\small O}\) i paralelna je s ravninom slike \( {\small \Pi}\). Sve točke te ravnine projiciraju se u beskonačno daleke točke ravnine \( {\small \Pi}\), stoga tu ravninu nazivamo izbježnom ravninom i označavamo je \({\small \Pi_i}\).
Kao što je u uvodu napomenuto, položaj točke u prostoru nećemo moći jednoznačno odrediti samo na temelju njezine centralne projekcije. Međutim, ako točka leži na nekom pravcu, njezina će projekcija ležati na projekciji tog pravca (\({\small T\in p \Rightarrow T_c\in p_c }\)). Zato ćemo prvo odrediti projekciju pravca, tako da temeljem nje možemo jednoznačno odrediti položaj pravca u prostoru, a zatim projekciju točke na tom pravcu.
Projiciranje pravca i točke
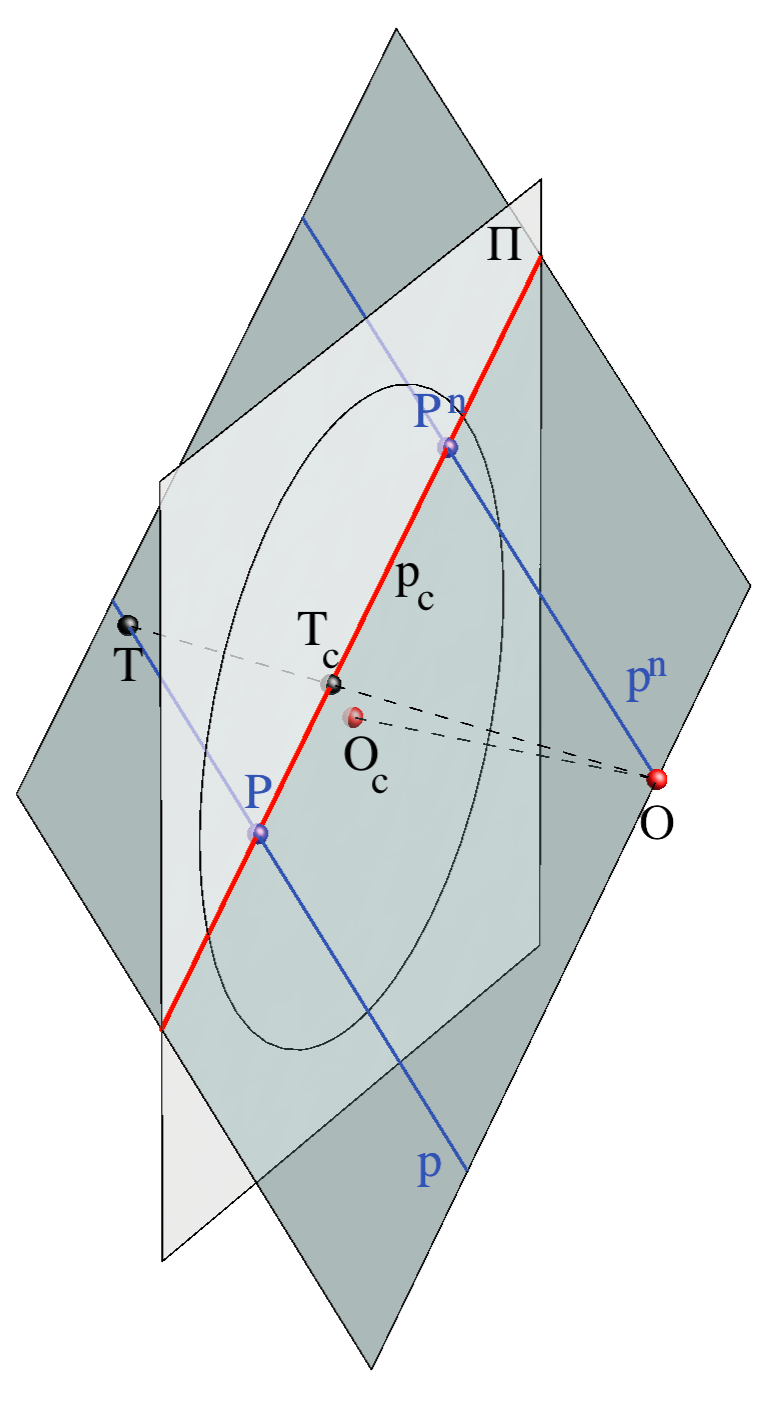
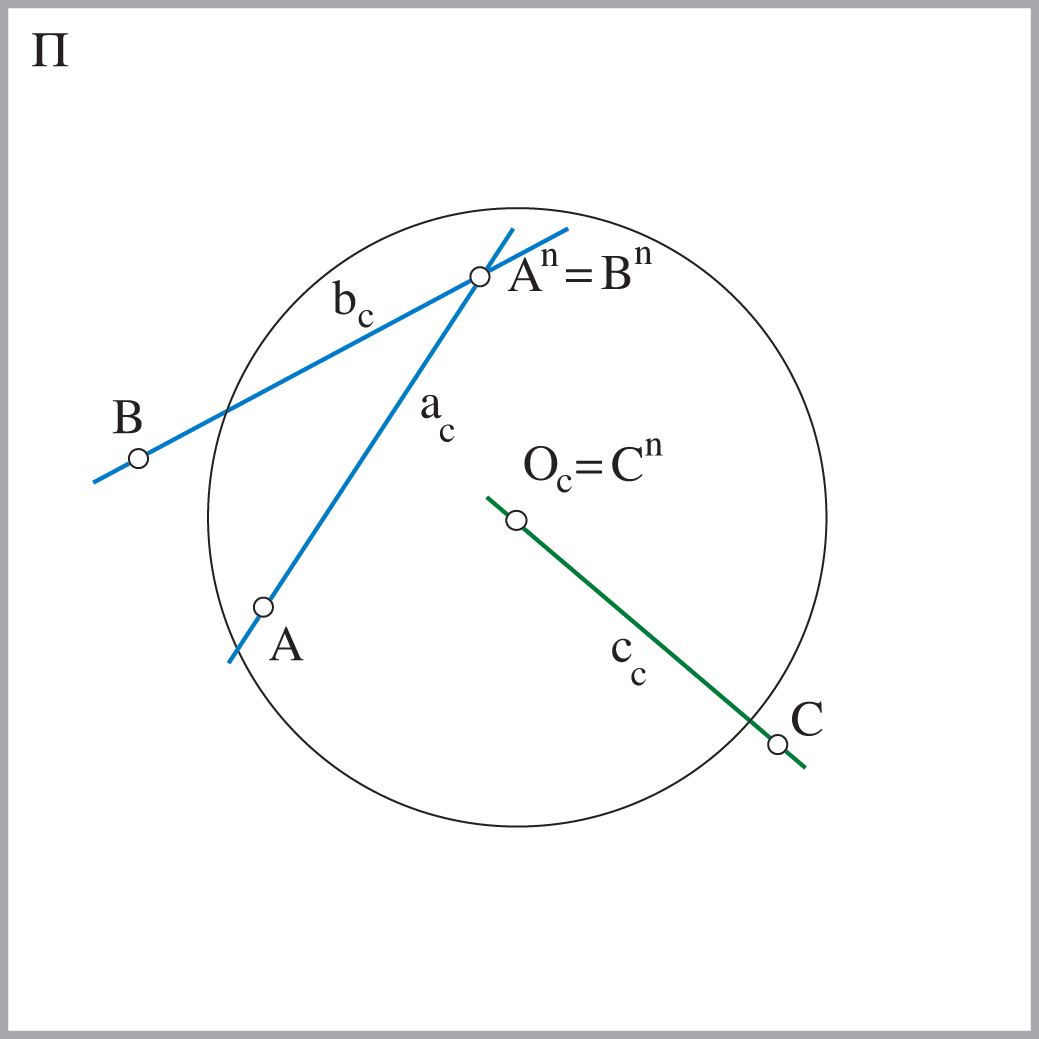
Za neki pravac \({\small p }\) koji je u općem položaju prema ravnini \({\small \Pi }\) i točki \({\small O }\), koji su odredbeni elementi projekcije, definiramo sljedeće elemente i oznake:
\({\small p }\) \(-\) bilo koji pravac u općem položaju prema odredbenim elementima projekcije
\({\small p^n }\) \(-\) nedogledni pravac pravca \({\small p }\) (prolazi očištem i paralelan je s pravcem \({\small p }\))
\({\small P }\) \(-\) pravo probodište pravca \({\small p }\) (probodište pravca \({\small p }\) i ravnine slike)
\({\small P^n }\) \(-\) nedogled pravca \({\small p }\) (probodište nedoglednog pravca \({\small p^n }\) i ravnine slike, odnosno perspektivna slika beskonačno daleke točke pravca \({\small p }\))
\({\small p_c }\) \(-\) centralna projekcija pravca \({\small p }\)
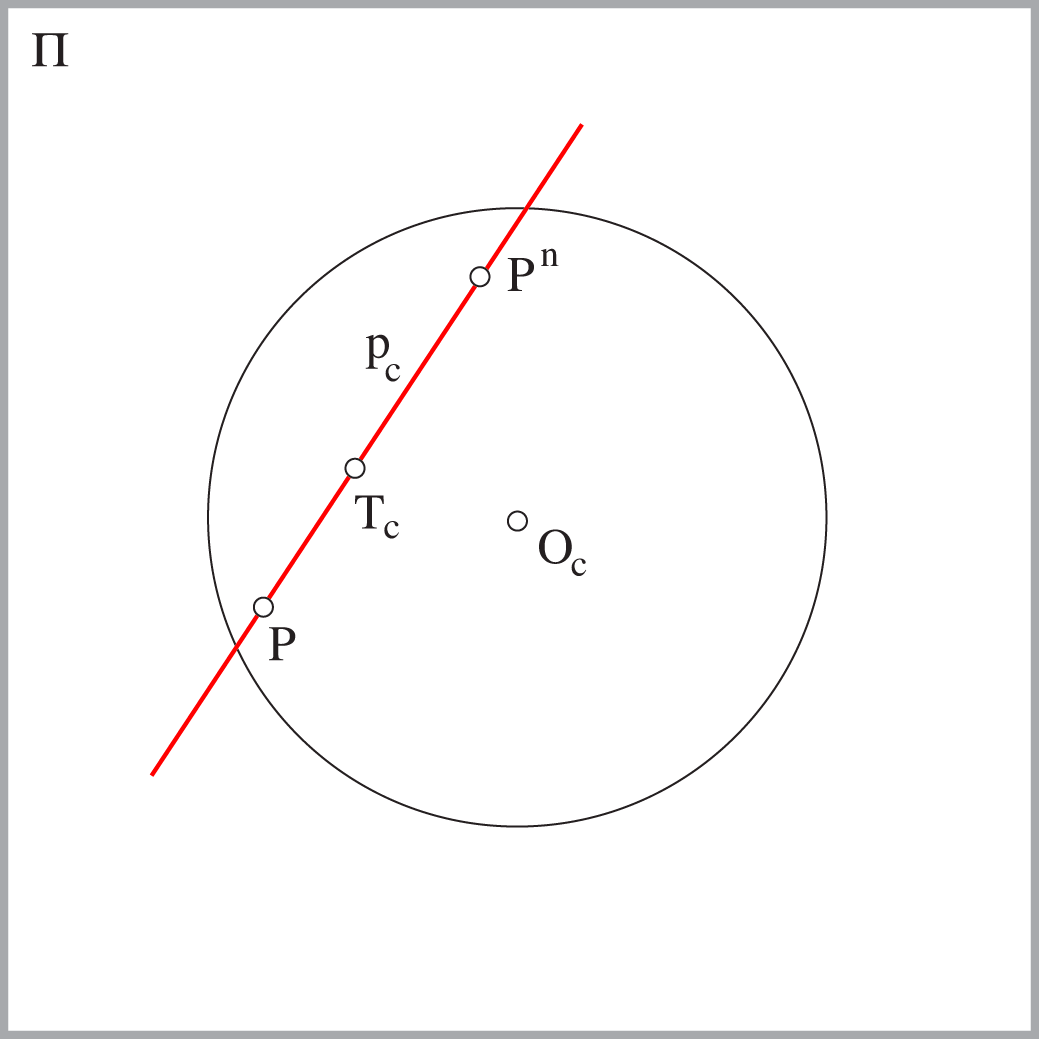
- Pravac \({\small p }\), koji je u općem položaju prema očištu i ravnini slike, u perspektivi prikazujemo tako da na njegovoj centralnoj projekciji \({\small p_c }\) istaknemo nedogled \({\small P^n }\) i pravo probodište \({\small P}\)
- Točku u perspektivi prikazujemo tako da istaknemo projekciju jednog pravca na kojem leži. Taj pravac nazivamo njezinim nositeljem
Taj način prikazivanja pravaca i točaka omogućuje jednoznačnu rekonstrukciju prostornog položaja tih elemenata na temelju njihove ravninske slike (vidi slike 260 i 261).
Izbježna točka pravca \({\small p }\) je njegovo probodište s izbježnom ravninom. Ta se točka projicira u beskonačno daleku točku pravca \({\small p_c }\).
Svojstva:
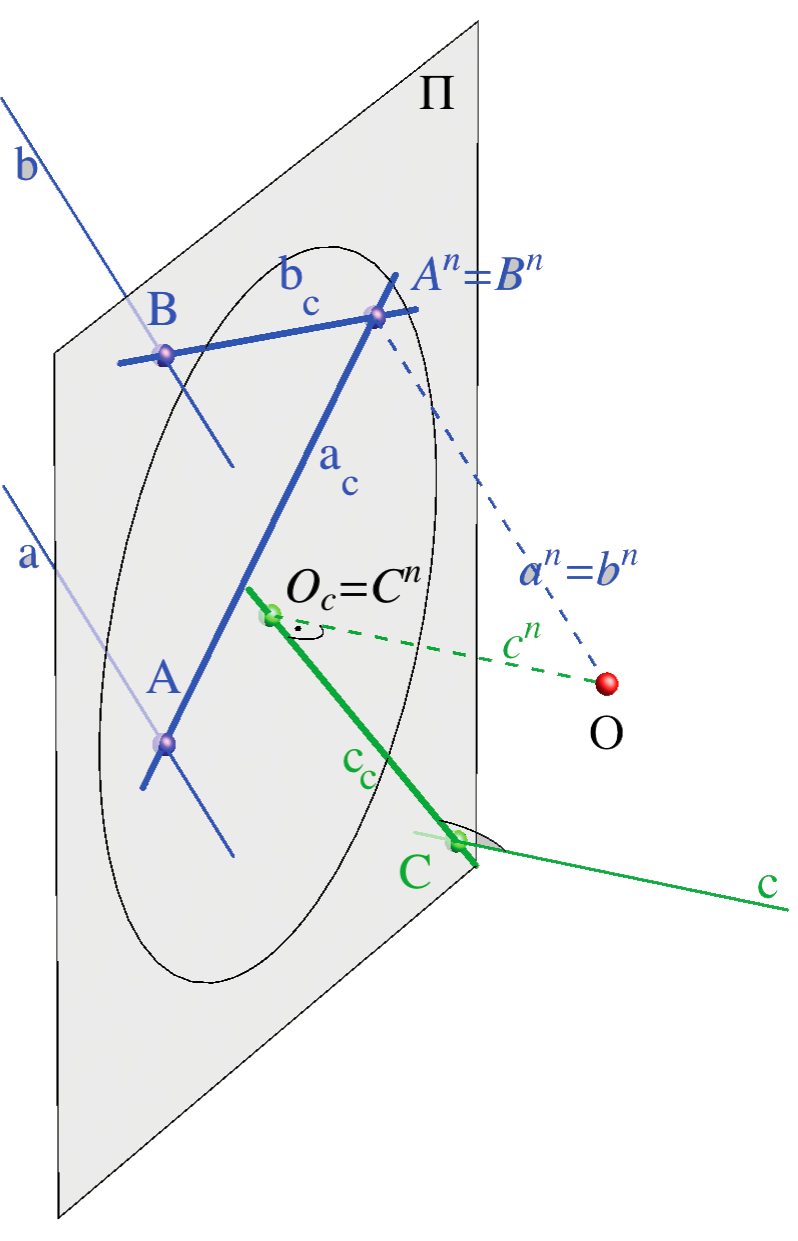
- Paralelni pravci imaju isti nedogled, odnosno \({\small a\parallel b \Leftrightarrow A^n=B^n }\)
- Pravci okomiti na ravninu slike imaju nedogled u glavnoj točki, odnosno \({\small c\perp \Pi \Leftrightarrow C^n=O_c }\)
Posebni pravci
- Vidni pravac (zraka projiciranja) projicira se u točku, odnosno u svoje probodište s ravninom slike
- Svi pravci izbježne ravnine projiciraju se u beskonačno daleki pravac ravnine slike
- Pravci paralelni s ravninom slike nemaju u konačnosti niti probodište niti nedogled - obje se točke podudaraju s njihovom beskonačno dalekom točkom. Kasnije ćemo prikazati način njihova zadavanja, jer će njihovi nositelji biti ravnine
Ravnina
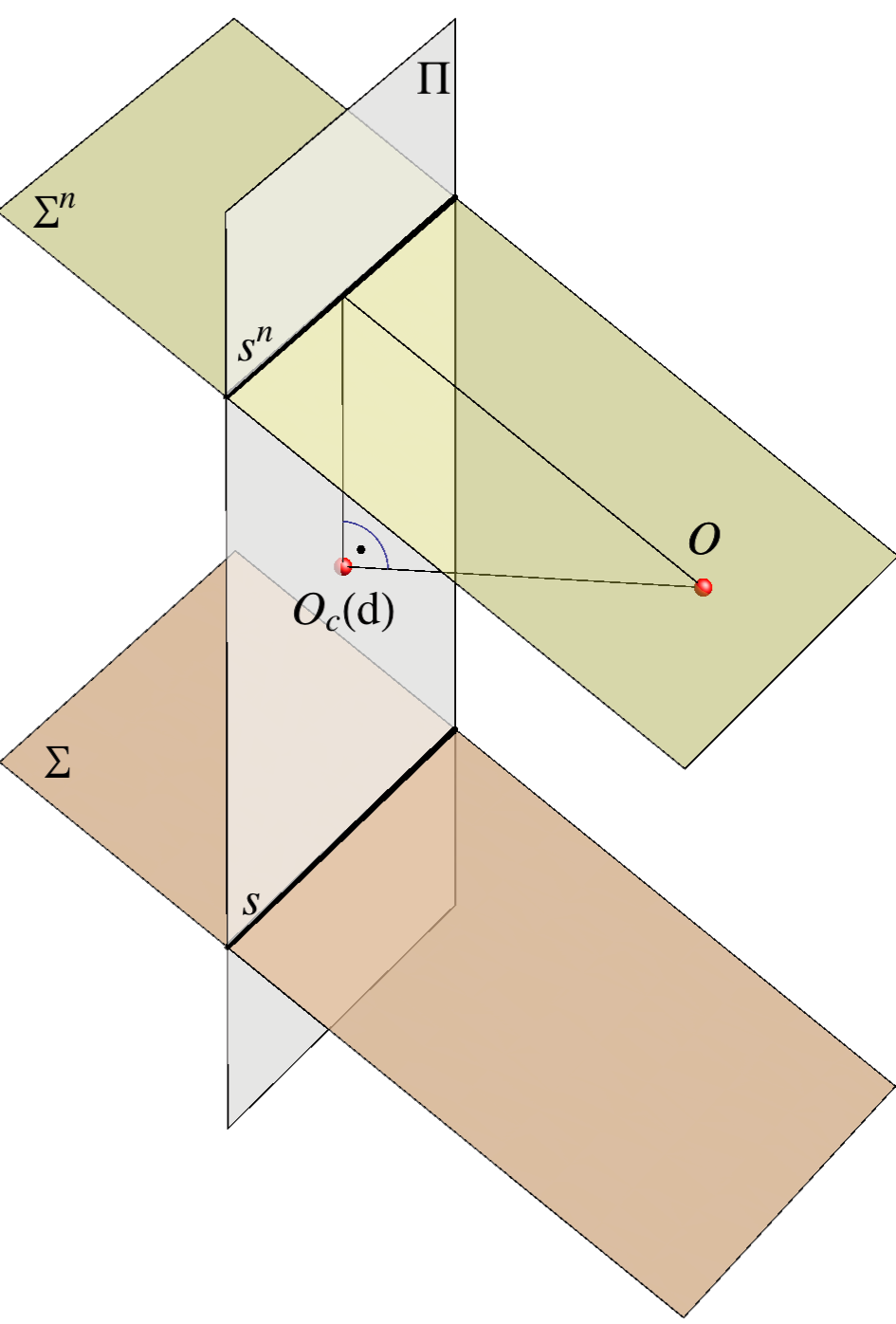
Za ravninu \({\small \Sigma }\), koja je u općem položaju prema ravnini \({\small \Pi }\) i točki \({\small O }\), definiramo sljedeće elemente i oznake:
\({\small \Sigma }\) \(-\) bilo koja ravnina koja ne sadrži očište i nije paralelna s ravninom slike
\({\small \Sigma^n }\) \(-\) nedogledna ravnina ravnine \({\small \Sigma }\) (prolazi očištem i paralelna je s ravninom \({\small \Sigma }\))
\({\small s }\) \(-\) pravi trag ravnine \({\small \Sigma }\) (presječnica ravnine \({\small \Sigma }\) i ravnine slike)
\({\small s^n }\) \(-\) nedogledni trag ili nedoglednica ravnine \({\small \Sigma }\) (presječnica ravnina \({\small \Sigma^n }\) i \({\small \Pi }\))
- Ravninu \({\small \Sigma }\) u perspektivi zadajemo njenim pravim i nedoglednim tragom (\({\small s^n }\),\({\small s }\))
Svojstva
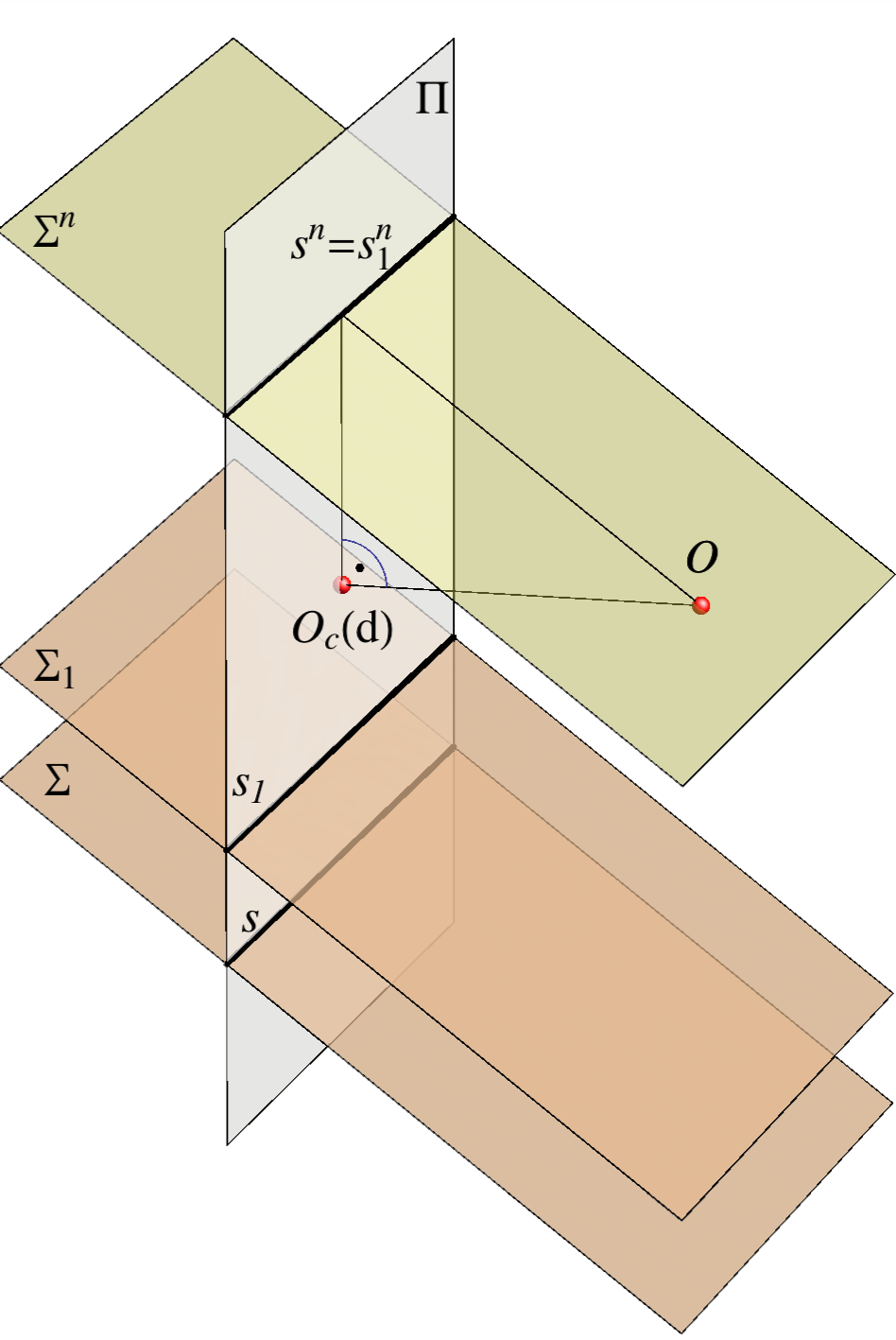
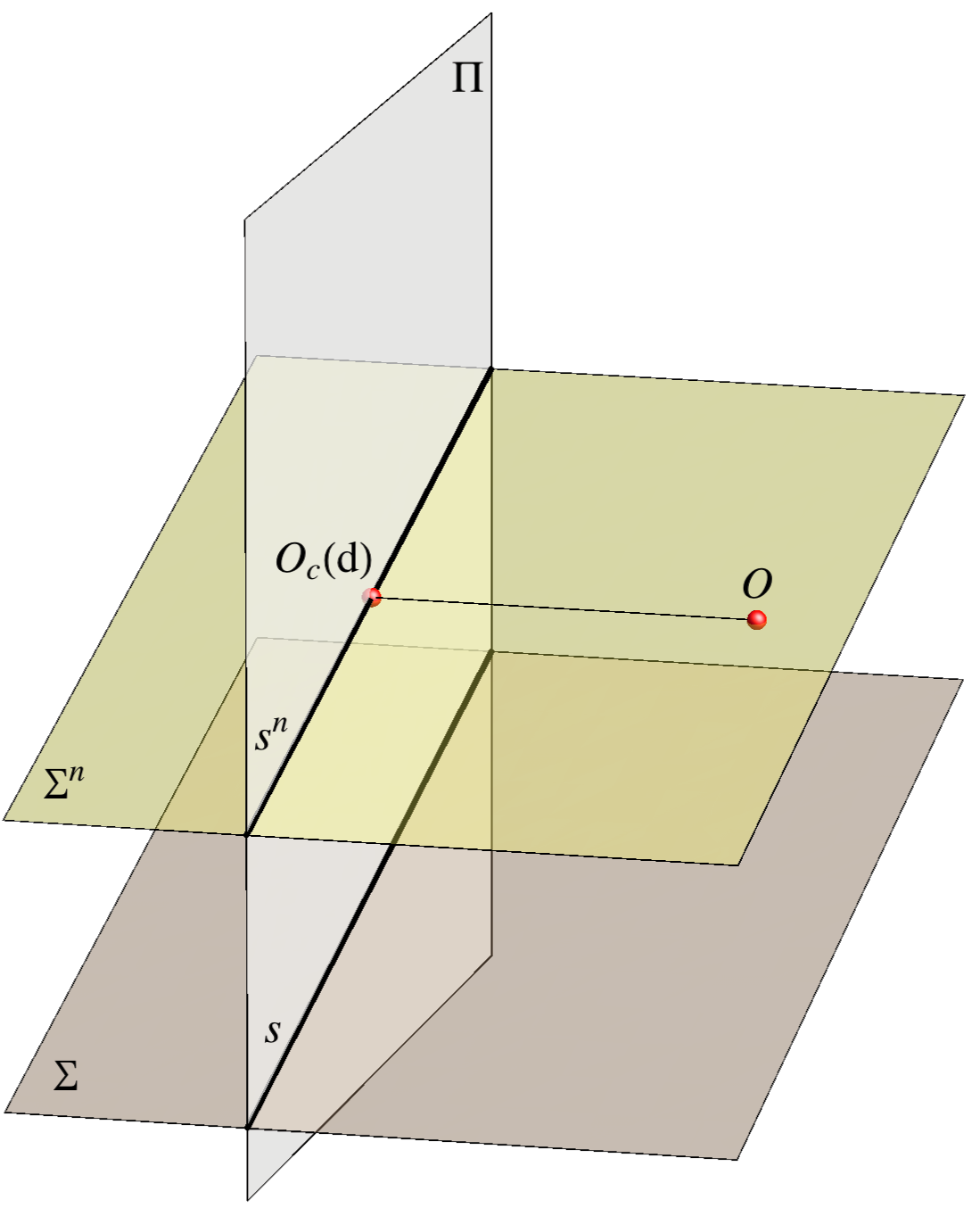
- Pravi i nedogledni trag uvijek su paralelni
- Paralelne ravnine imaju istu nedoglednicu, odnosno \({\small \mathbb A\parallel \mathbb B \Leftrightarrow a^n=b^n }\)
- Nedoglednica ravnine okomite na ravninu slike prolazi glavnom točkom, dakle \({\small \Sigma\perp \Pi \Leftrightarrow O_c\in s^n }\)
- Pravci ravnine koji su paralelni s ravninom slike (u ortogonalnim projekcijama nazivali smo ih sutražnicama) projiciraju se paralelno s tragovima ravnine. Ako je neka ravnina zadana svojim tragovima \({\small \Sigma (s,s^n) }\) tada centralna projekcija bilo koje njezine sutražnice \({\small a_c }\) jednoznačno određuje položaj te sutražnice u prostoru. Stoga, pravac paralelan s ravninom \({\small \Pi }\) zadavat ćemo njegovom projekcijom i tragovima bilo koje ravnine koja sadrži taj pravac
Međusobni odnosi točaka, pravaca i ravnina
- Pravac leži u ravnini ako mu je pravo probodište na pravom, a nedogled na nedoglednom pravcu ravnine, odnosno kada je \({\small p\subset \Sigma \Leftrightarrow P\in s \wedge P^n\in s^n }\)
- Pravac je paralelan s ravninom ako mu nedogled leži na nedoglednici ravnine, odnosno kada je \({\small p\parallel \Sigma \Leftrightarrow P^n\in s^n }\)
- Točka leži u ravnini ako leži na nekom pravcu te ravnine
- Paralelne ravnine imaju istu nedoglednicu, odnosno vrijedi \({\small \Delta\parallel \Sigma \Leftrightarrow d^n\in s^n }\)
- Pravo probodište presječnice dviju ravnina leži u sjecištu njihovih pravih tragova, dok je nedogled presječnice u sjecištu nedoglednica ravnina
Prikloni kut pravca i ravnine
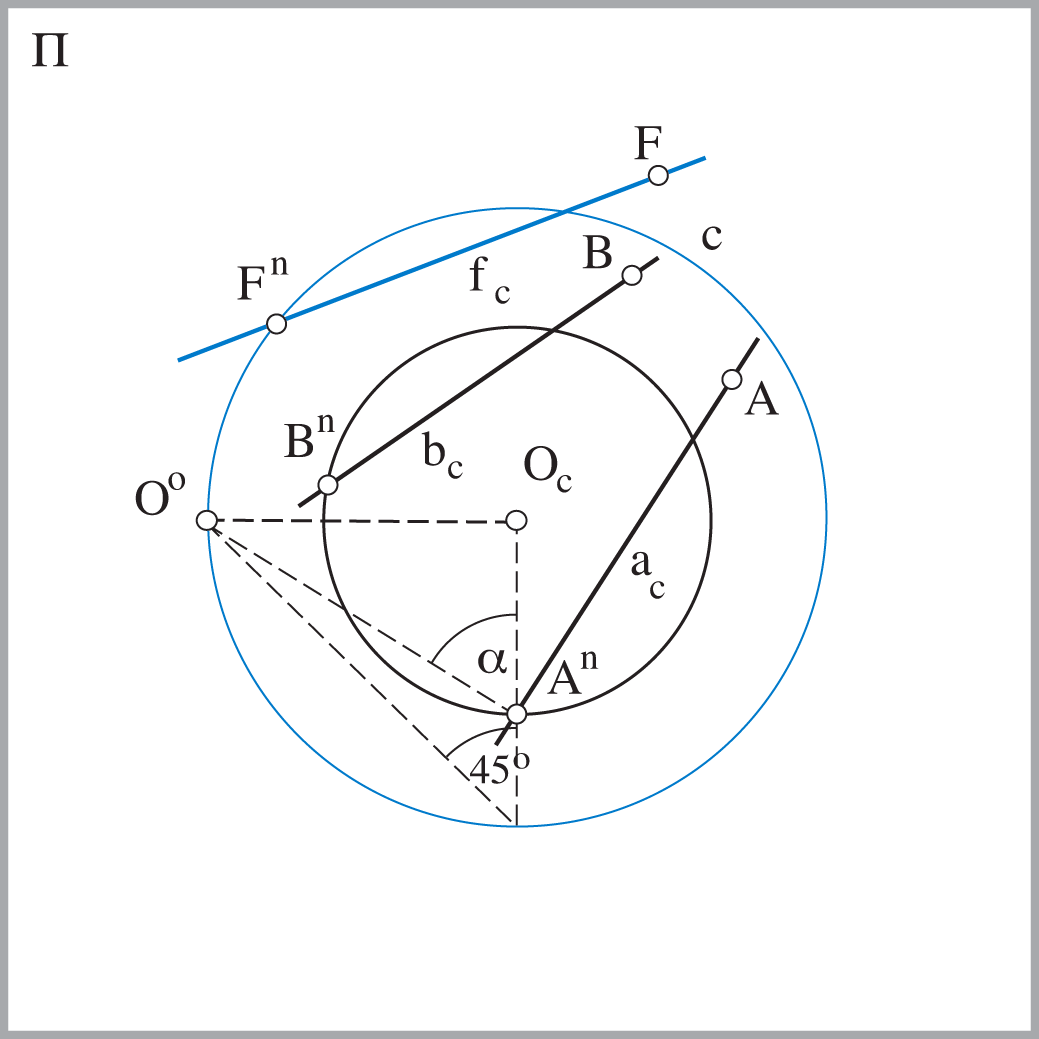
Pod priklonim kutom pravca (ravnine) podrazumijevamo kut što ga taj pravac (ravnina) zatvara s ravninom slike. Budući da paralelni pravci imaju iste priklone kutove, možemo zaključiti da je prikloni kut svakog pravca jednak priklonom kutu njegovog nedoglednog pravca. Na temelju toga zaključujemo sljedeće:
- Nedogledi svih pravaca kojima je prikloni kut 45o leže na distancijskoj kružnici
- Nedogledi svih pravaca koji imaju isti prikloni kut α leže na kružnici koja je koncentrična s distancijskom kružnicom

Priklonica ravnine je bilo koji njezin pravac koji je okomit na njezine tragove. Prikloni kut neke ravnine jednak je priklonom kutu bilo koje njezine priklonice.
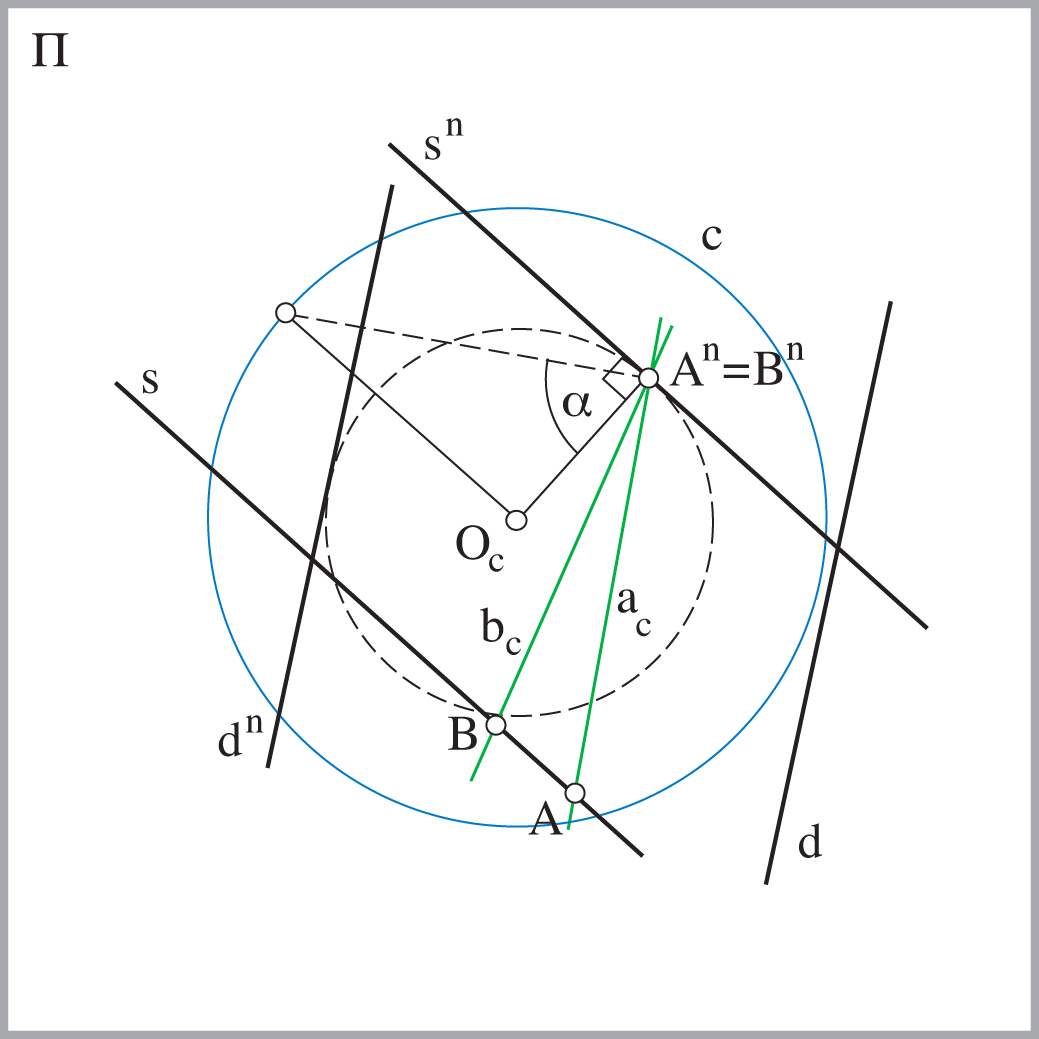
- Nožište okomice postavljene kroz glavnu točku \({\small O_c }\) na nedoglednicu \({\small s^n }\) ravnine \({\small \Sigma }\) je nedogled svih priklonica ravnine \({\small \Sigma }\)
- Nedoglednice ravnina koje imaju isti prikloni kut tangente su iste kružnice sa središtem u glavnoj točki
- Specijalno, tangente distancijske kružnice su nedoglednice ravnina koje s ravninom slike zatvaraju kut od \({\small 45^\circ }\), dok su pravci pramena \({\small O_c }\) nedoglednice ravnina okomitih na ravninu slike
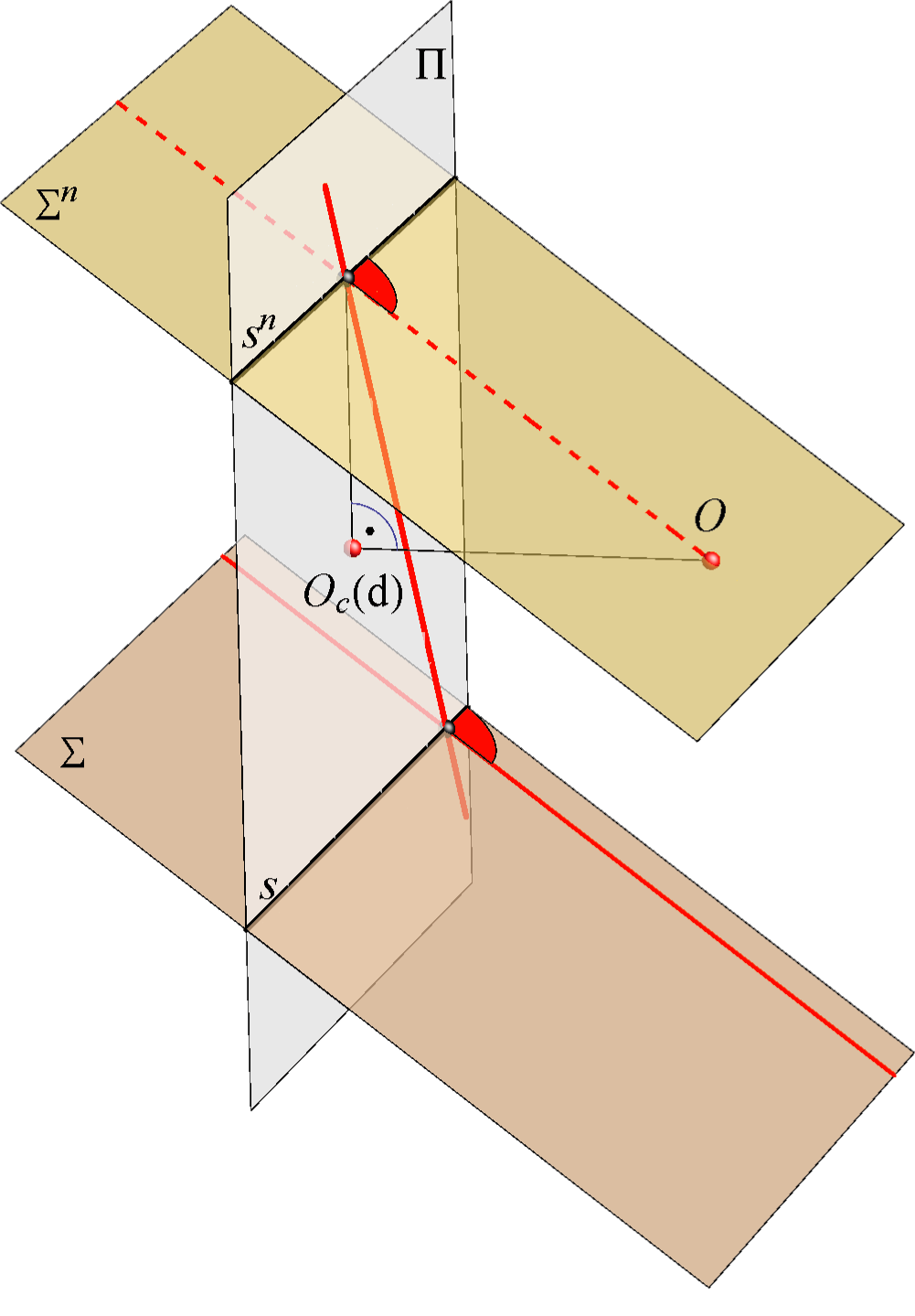
Okomitost pravca i ravnine
Za neku ravninu \(\small \Sigma\) nedogled svih pravaca koji su na nju okomiti (točka \(\small N_n\)) je probodište njezine normale kroz \(\small O\) i ravnine slike. Nedogledni pravac svih normala i nedogledni pravac svih priklonica ravnine \(\small \Sigma\) leže u ravnini koja je okomita na ravninu slike, a siječe ju po okomici iz \(\small O_c\) na tragove \(\small s\) i \(\small s_n\) (vidi sliku 271). Prevaljivanjem te ravnine u ravninu slike možemo konstruirati točku \(\small N_n\) (vidi sliku 272).

