
\( o\) – osnovica
pravi trag horizontalne ravnine
\( h\) – horizont
nedogledni trag horizontalne ravnine
\( \small D_1, D_2 \) – distancijske točke
nedogledi pravaca horizontalne ravnine s priklonim kutem od \( 45^\circ\)
Prava veličina nekih dužina
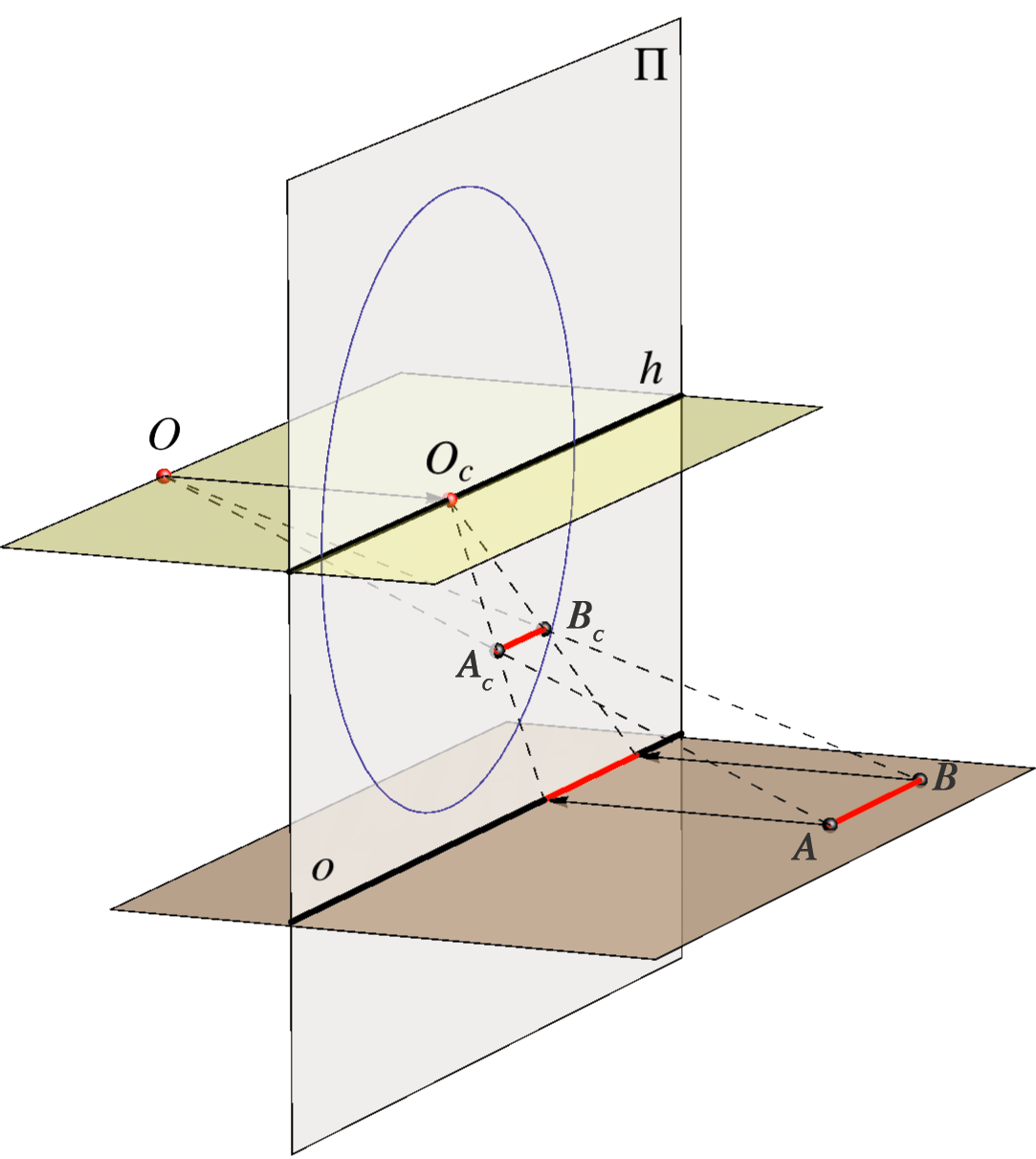
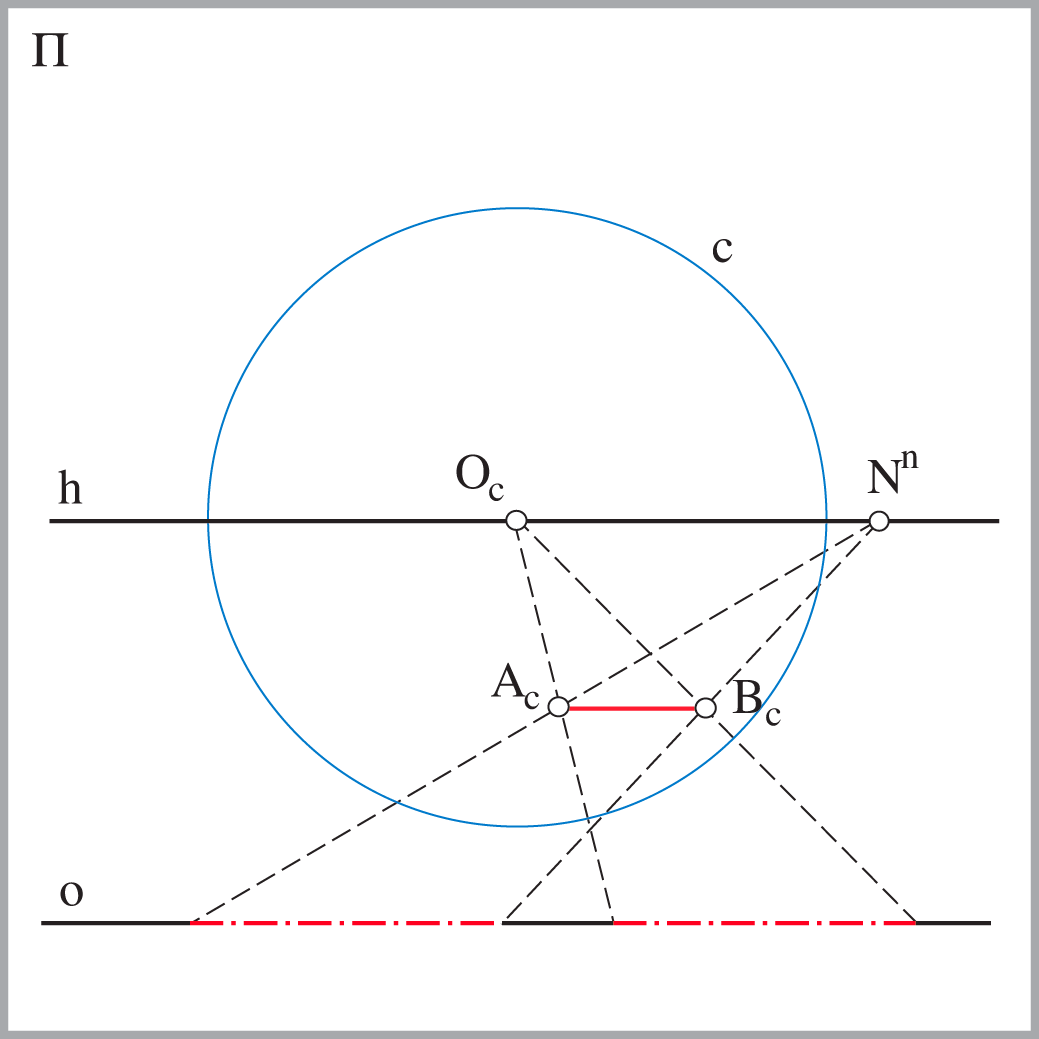
Pravu veličinu dužine \( {\small \overline{AB}}\) koja leži u horizontalnoj ravnini i paralelna je s ravninom slike, možemo odrediti tako da njezinu perspektivnu sliku \( {\small \overline{A_cB_c}}\) projiciramo na osnovicu \( {\small o}\) iz bilo koje točke horizonta \( {\small h}\).

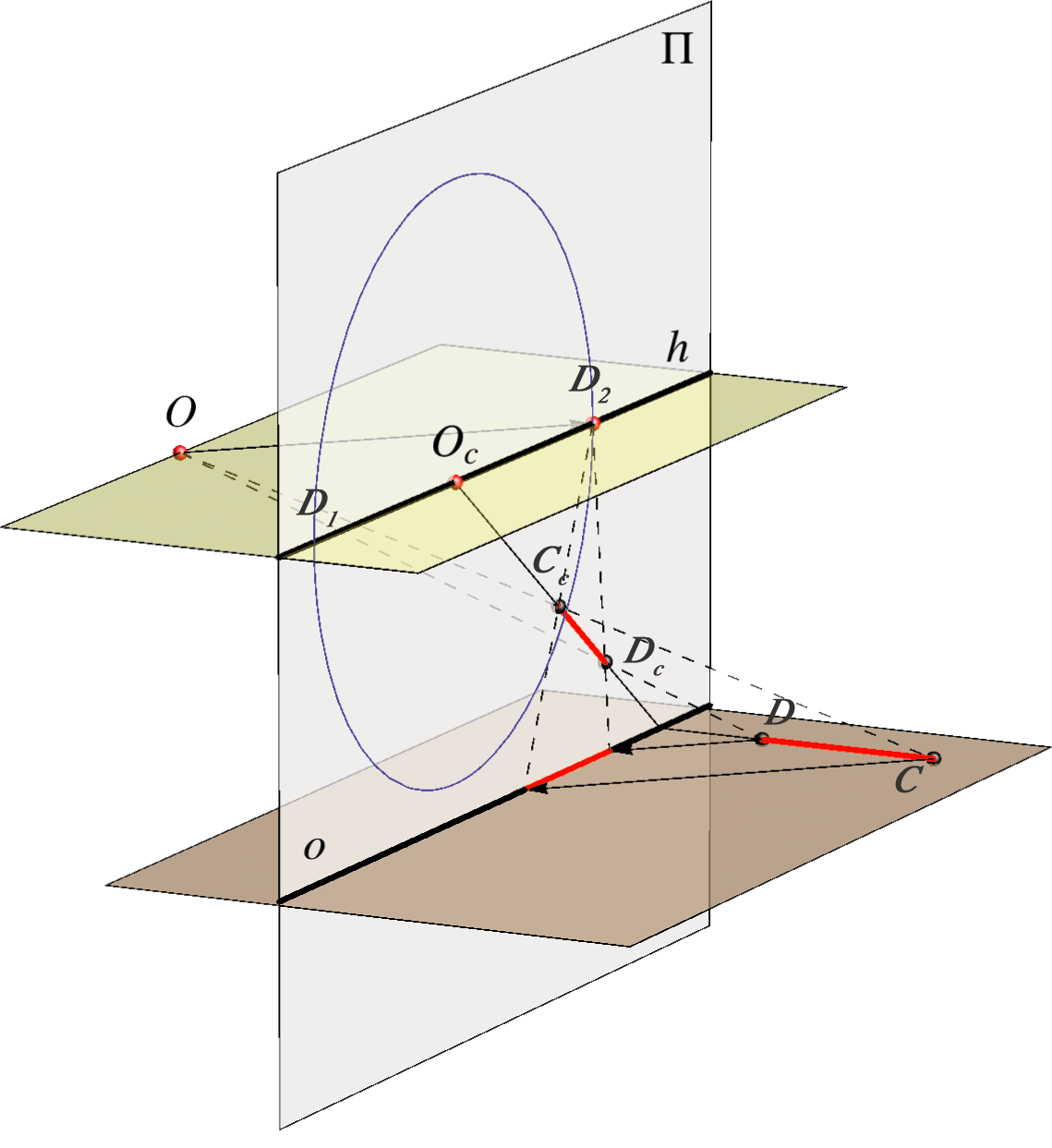
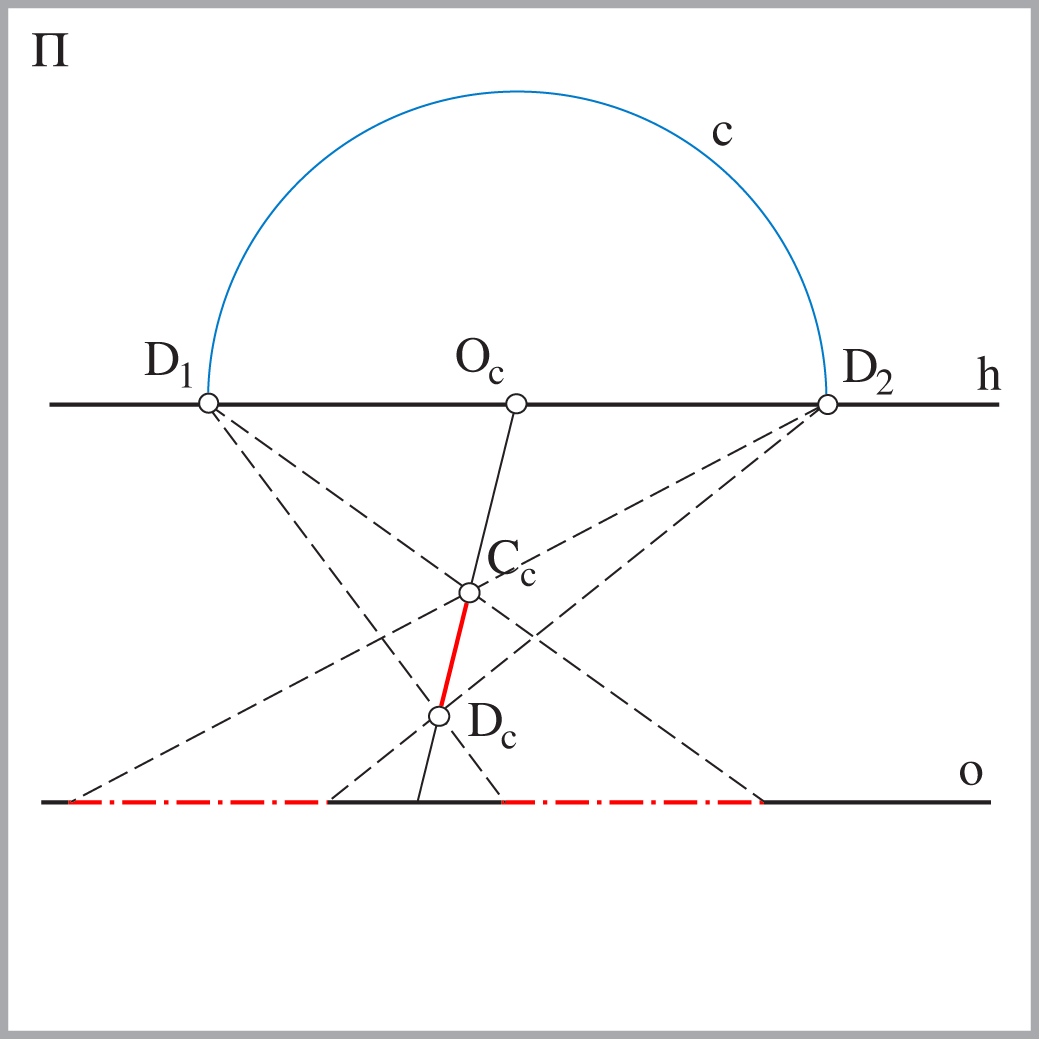
Pravu veličinu dužine \( {\small \overline{CD}}\) koja leži u horizontalnoj ravnini i okomita je na ravninu slike, možemo odrediti tako da njezinu perspektivnu sliku \( {\small \overline{C_cD_c}}\) projiciramo na osnovicu \( {\small o}\) iz distancijske točke \( {\small D_1}\) ili \( {\small D_2}\).
Pravu veličinu dužine \( {\small \overline{EF}}\) koja je okomita na horizontalnu ravninu, a točka \( {\small E}\) joj leži u horizontalnoj ravnini, određujemo na način koji je prikazan na donjim slikama 279-281.

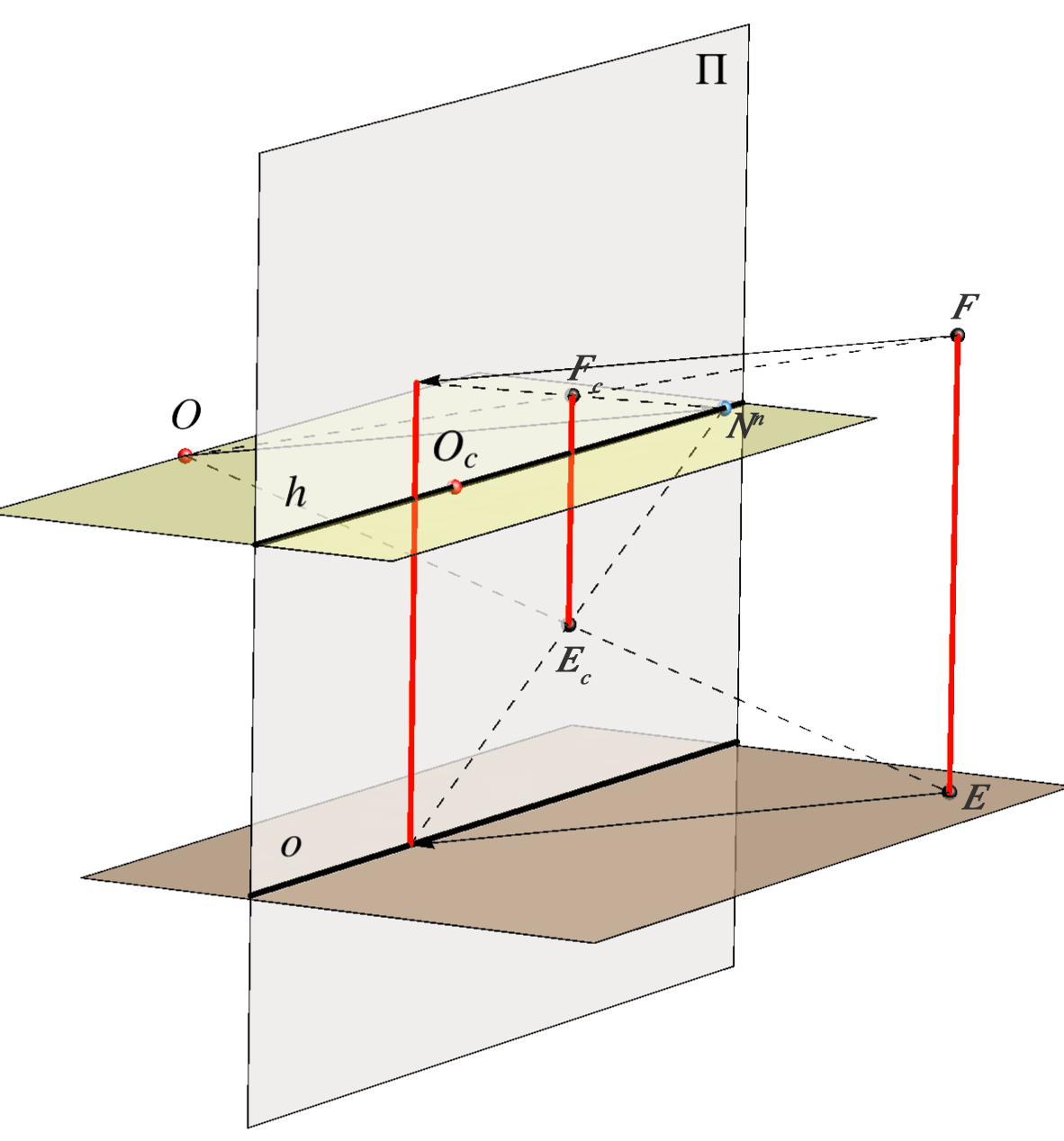

Prevaljivanje horizontalne ravnine u ravninu slike
PONOVITE: Perspektivna kolineacija
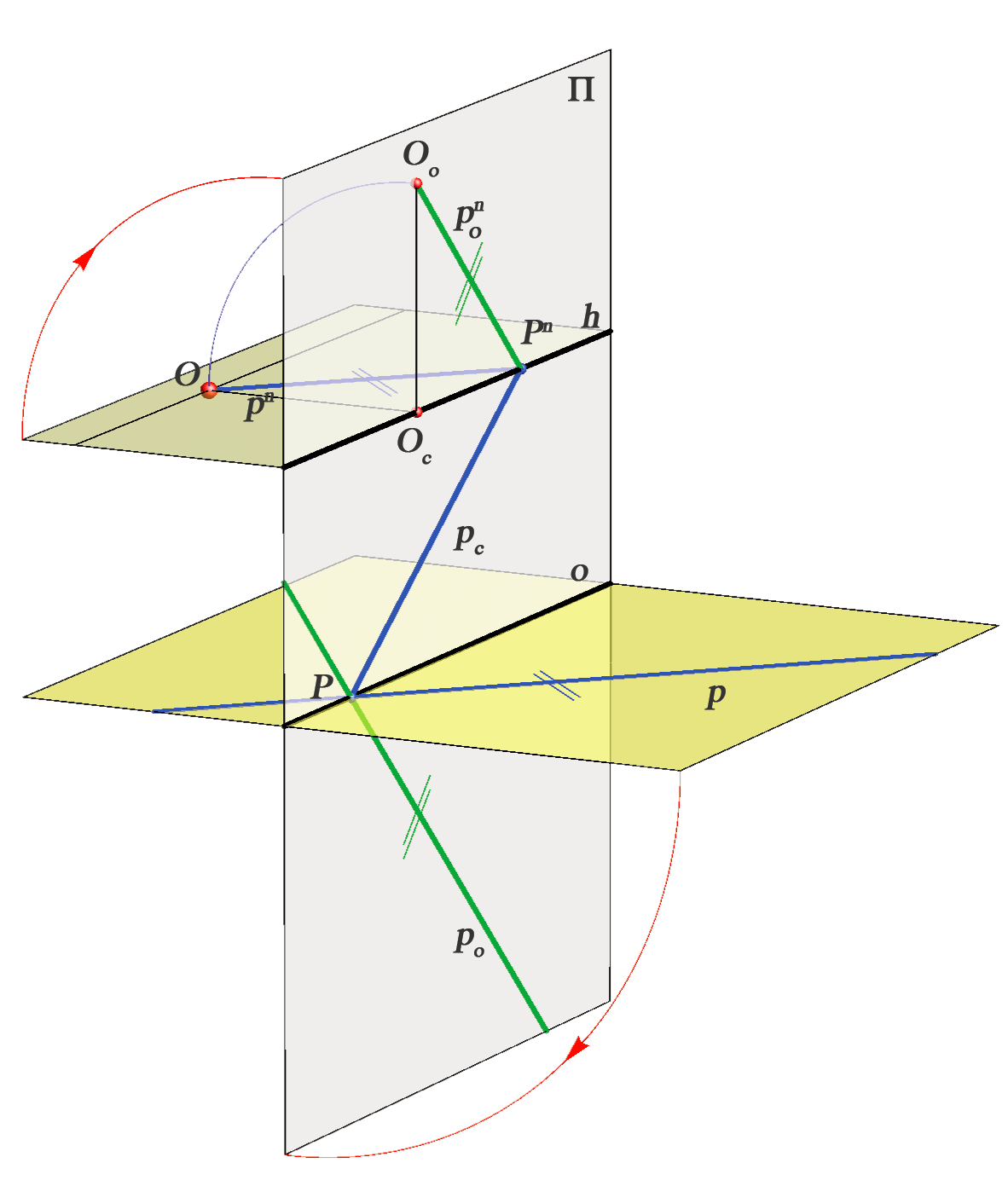
Za konstrukciju slike nekog objekta važno je znati konstruirati pravu veličinu geometrijske figure koja leži u horizontalnoj ravnini. Pod pojmom prevaljivanja horizontalne ravnine u ravninu slike podrazumijevamo njezinu rotaciju za kut od \(90^\circ\) oko osnovice \(o\). Da bismo došli do što jednostavnijih konstrukcijskih postupaka i horizontalnu ravninu kroz očište također rotiramo za \(90^\circ\), ali oko horizonta \(h\). Položaje rotiranih elemenata označavat ćemo donjim znakom \(\circ\).
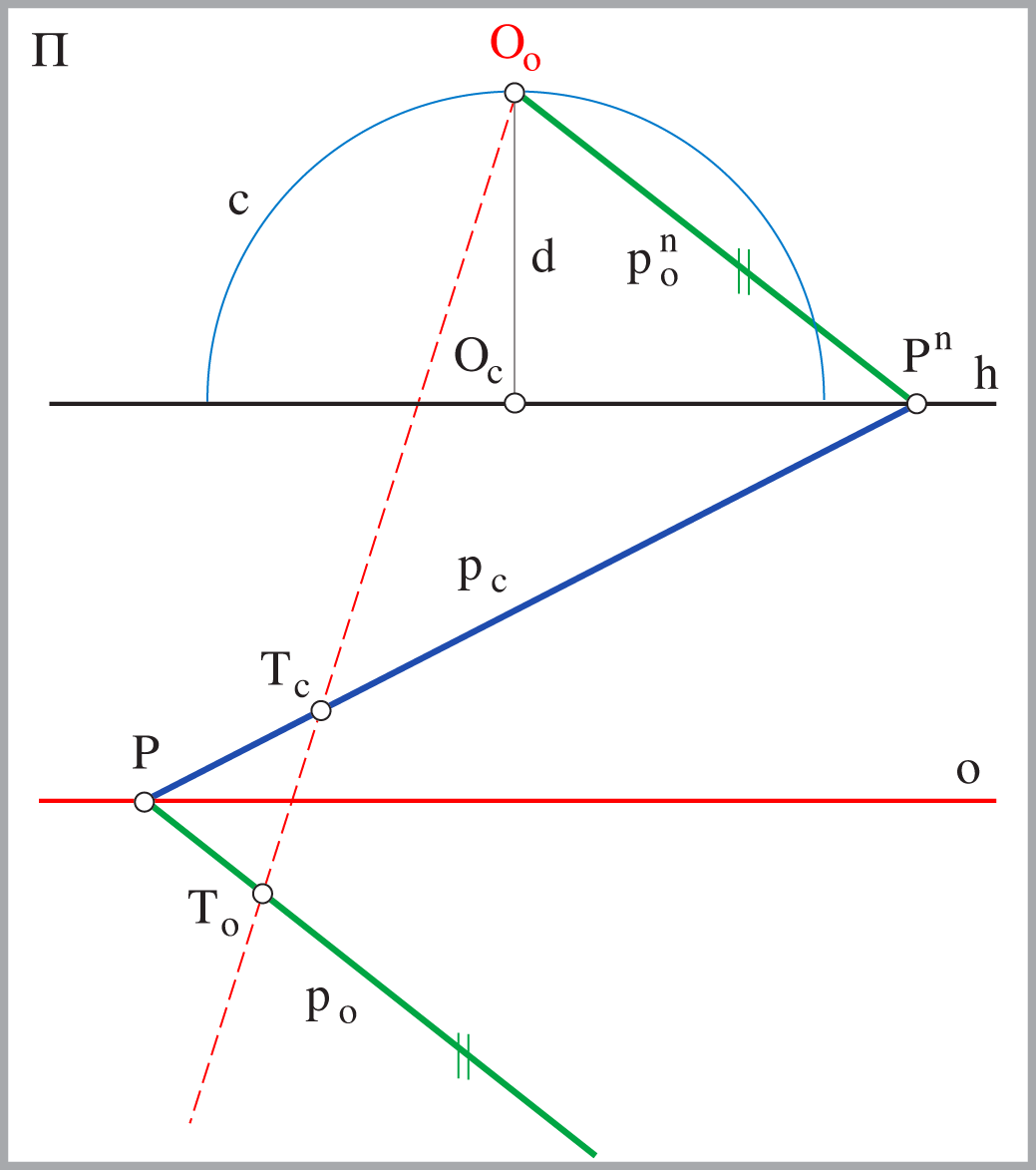
Sa slike 282 može se zaključiti da vrijedi sljedeće:
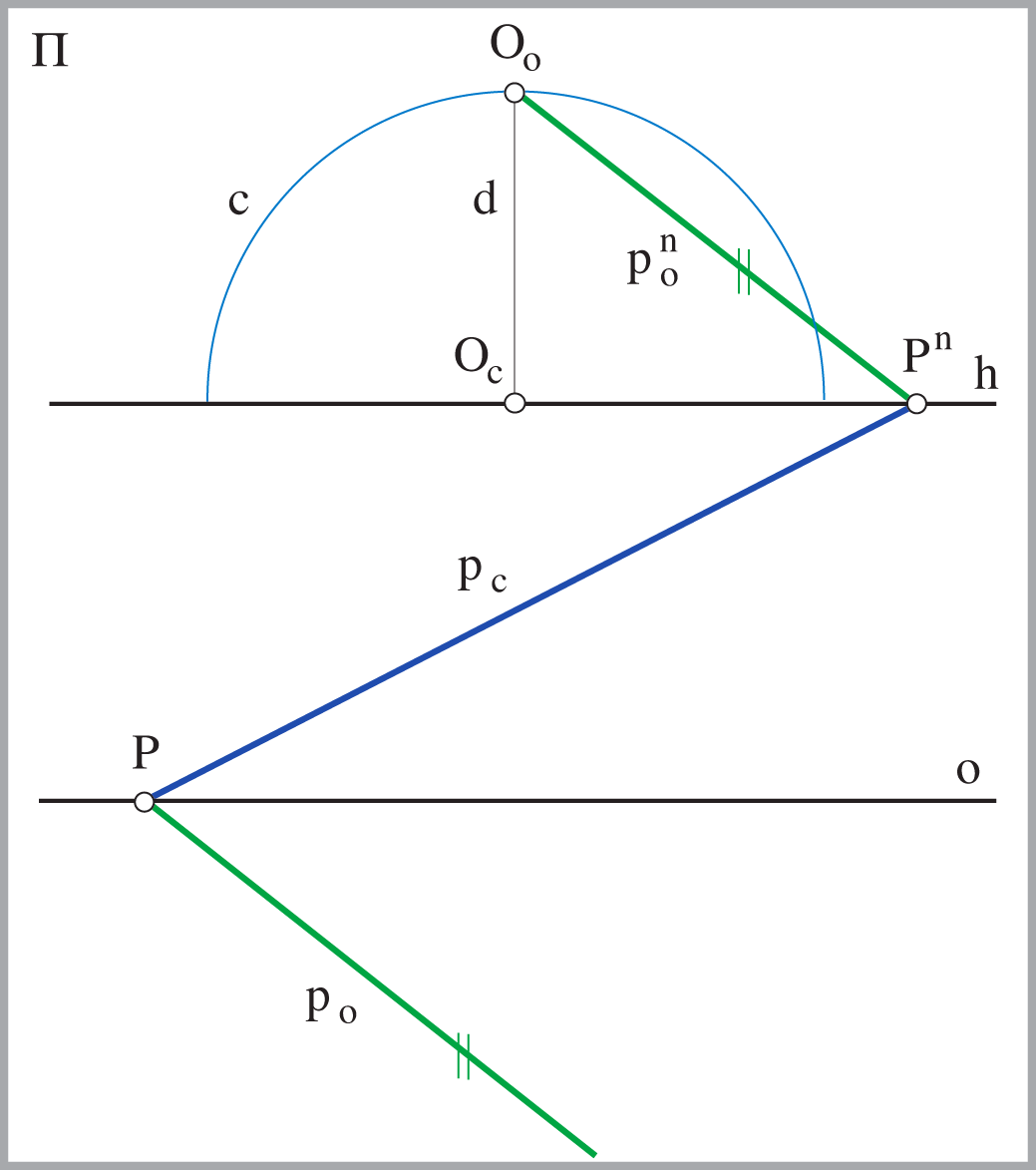
- Za svaki pravac \(\small p(P,P^n)\) horizontalne ravnine, koji je u općem položaju prema zadanim elementima projekcije, vrijedi da je \(\small p_\circ\) paralelan sa spojnicom \(\small O_\circ P^n\), odnosno \(\small p_\circ \parallel O_\circ P^n\)
Na slici 284 možemo uočiti da za pridruživanje \(\small T_c \longleftrightarrow T_\circ \) vrijedi da sve spojnice \(\small T_c T_\circ \) prolaze točkom \(\small O_\circ\), da su sve točke osnovice \(\small o\) same sebi pridružene te da se parovi pridruženih pravaca \(\small (p_c, p_\circ) \) sijeku na osnovici \(\small o\). Na temelju toga zaključujemo:
- Za svaku točku \(\small T\) horizontalne ravnine, koja je u općem položaju prema zadanim elementima projekcije, vrijedi da je bijekcija \(\small T_c \longleftrightarrow T_\circ \) perspektivna kolineacija kojoj je \(\small O_\circ\) središte, a pravac \(\small o\) os. Tako zadanu perspektivnu kolineaciju označavamo \(\small (O_\circ, o, T_c, T_\circ )\)
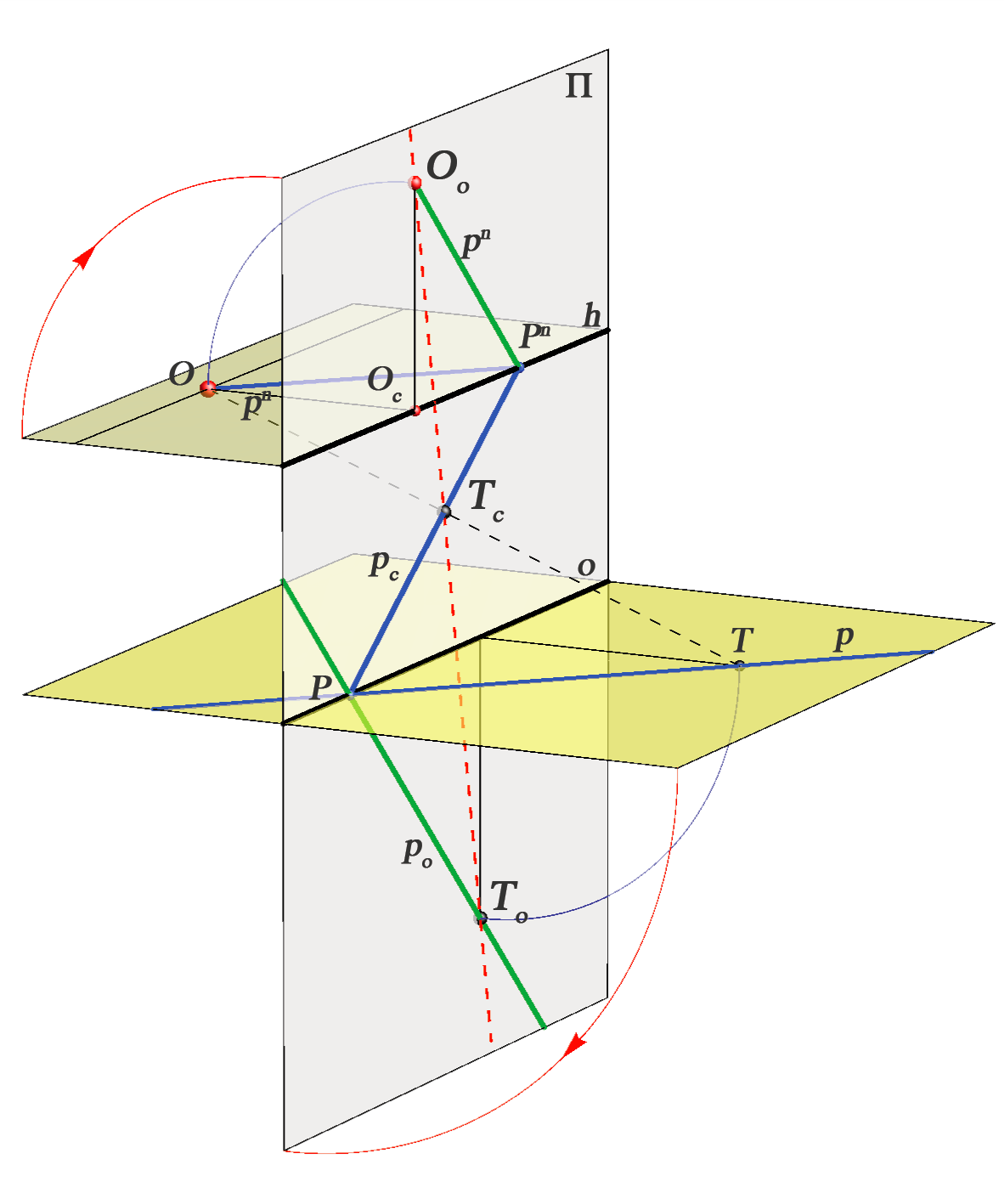
Pravac ravnine čije se točke projiciraju u beskonačno daleke točke ravnine slike nazivamo izbježnicom ravnine. On je presječnica promatrane i izbježne ravnine.
Pravac \(\small i_\circ\), rotirana izbježnica horizontalne ravnine, je paralela s osnovicom koja je od nje udaljena za distanciju \(\small d\).
Taj je pravac ujedno i izbježni pravac perspektivne kolineacije \(\small (O_\circ, o, T_c, T_\circ )\).

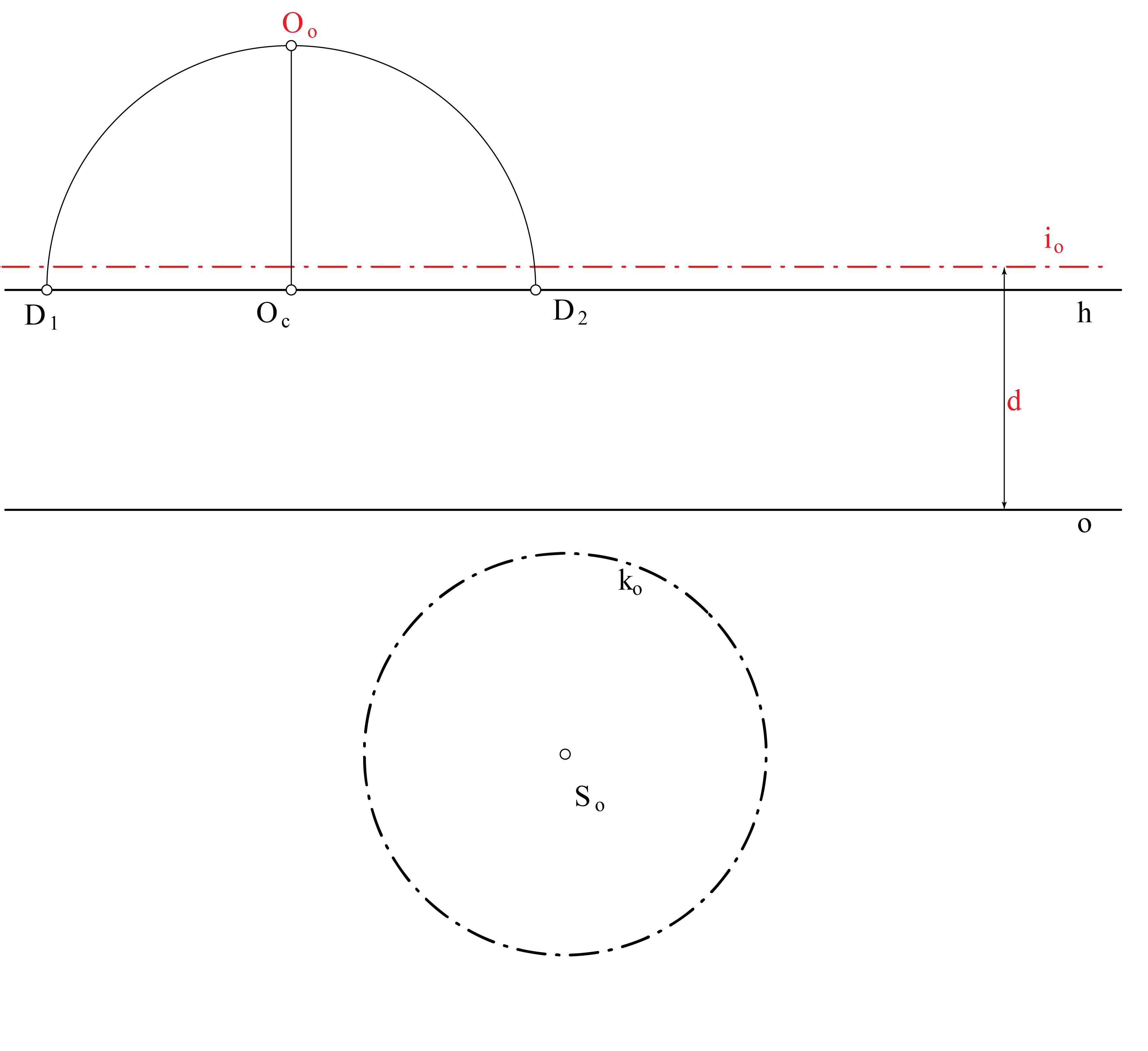
Kružnica u horizontalnoj ravnini
PONOVITE: Klasifikacija konikaPretpostavimo da kružnica \(\small k\) leži u ravnini koja ne sadrži očište \(\small O\). Svaka takva kružnica ima s izbježnom ravninom dvije zajedničke točke koje leže na izbježnici njezine ravnine. Ovisno o tome da li su te dvije presječne točke konjugirano imaginarne, realne i podudarne ili realne i različite, konika \(\small k_c\) je redom elipsa, parabola ili hiperbola. Slično zaključujemo i ako koniku \(\small k_c\) promatramo kao presjek ravnine \(\small \Pi\) i stošca određenog kružnicom \(\small k\) te vrhom \(\small O\). Konika \(\small k_c\) je elipsa, parabola ili hiperbola, ako izbježna ravnina \(\small \Pi_i\) siječe spomenuti stožac redom u dvije konjugirano imaginarne, realne i podudarne ili realne i različite izvodnice. Vidi slike 287-289.
Ako kružnica leži u ravnini koja sadrži očište \(\small O\), njezina je slika dužina ili pravac. Specijalno, ako leži u izbježnoj ravnini, njezina je slika beskonačno daleki pravac ravnine slike.
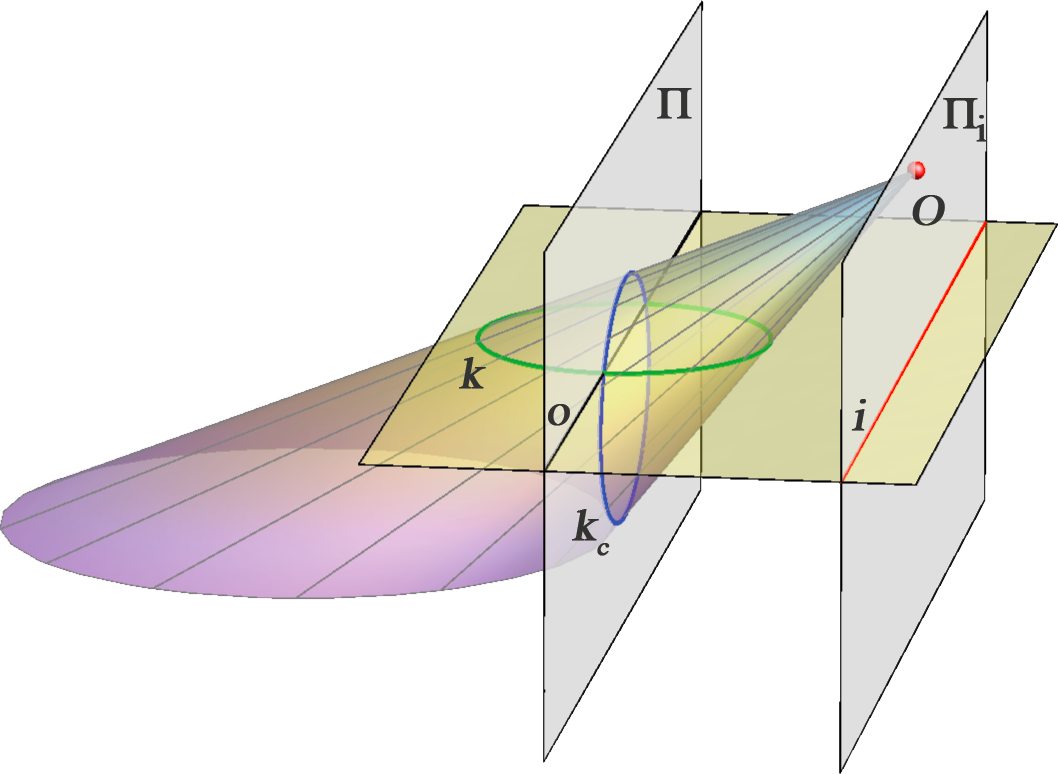
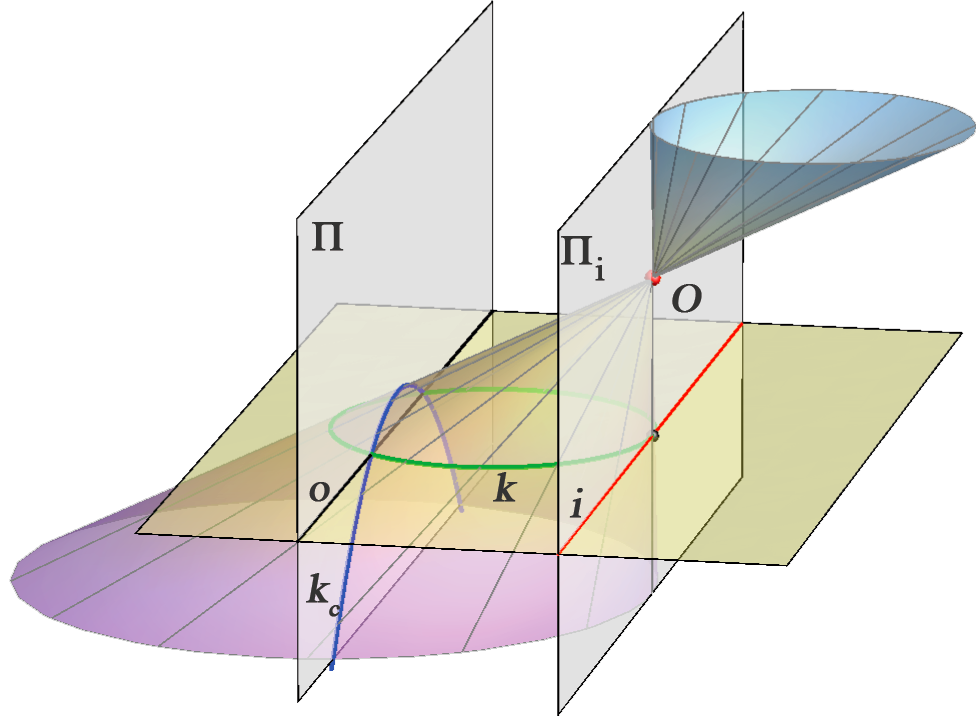
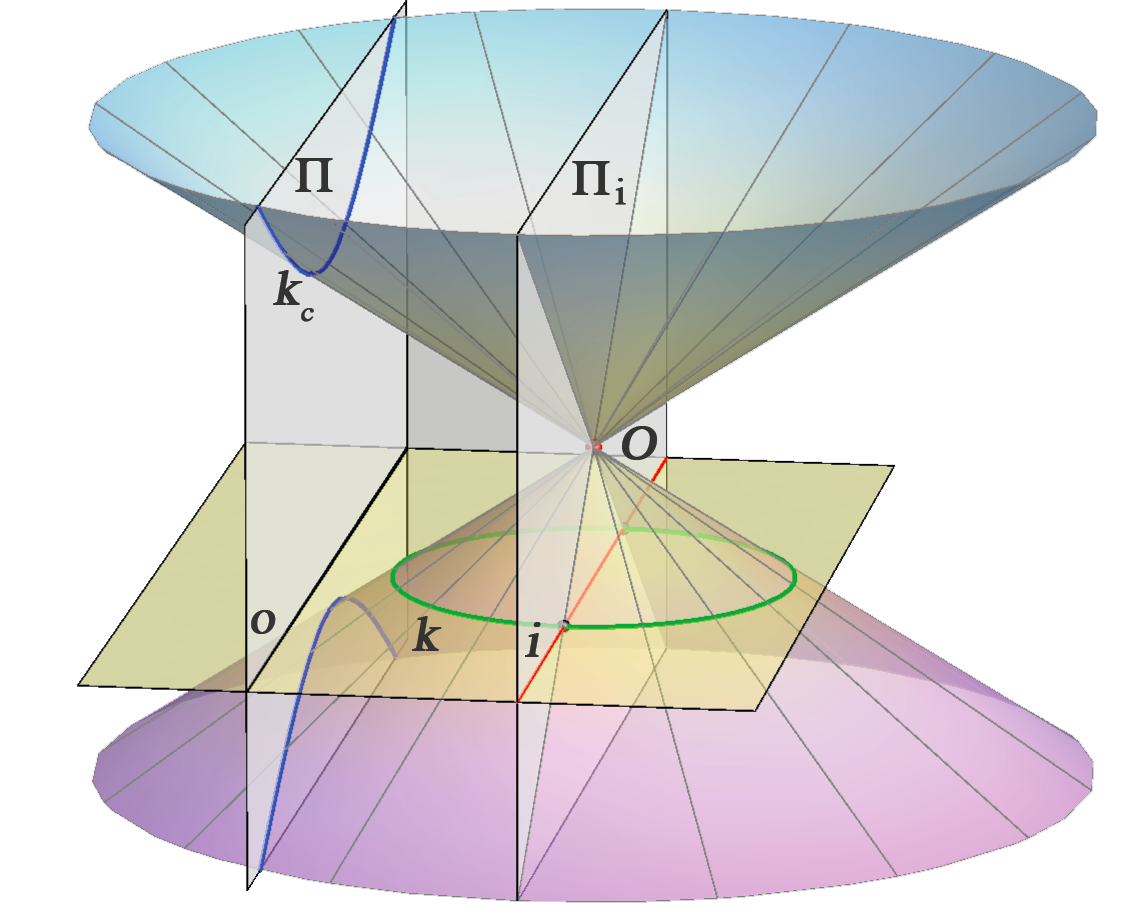
Zadatak: Kružnica \(\small k\) leži u horizontalnoj ravnini, a na slici je zadana svojim rotiranim položajem \(\small (S_\circ, k_\circ )\). Nacrtajte koniku \(\small k_c\) pomoću njezinih osam tangenata s diralištima.





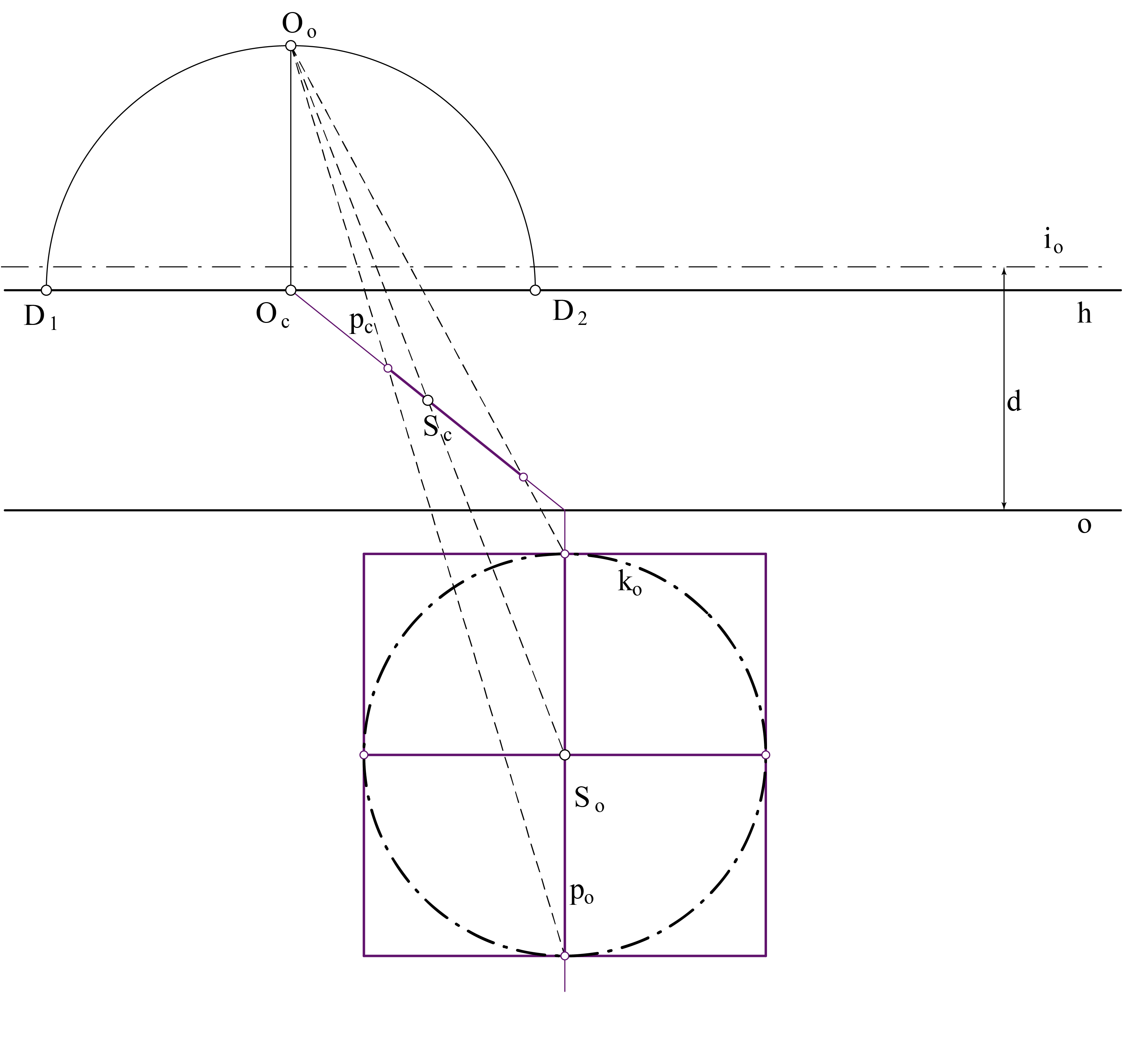


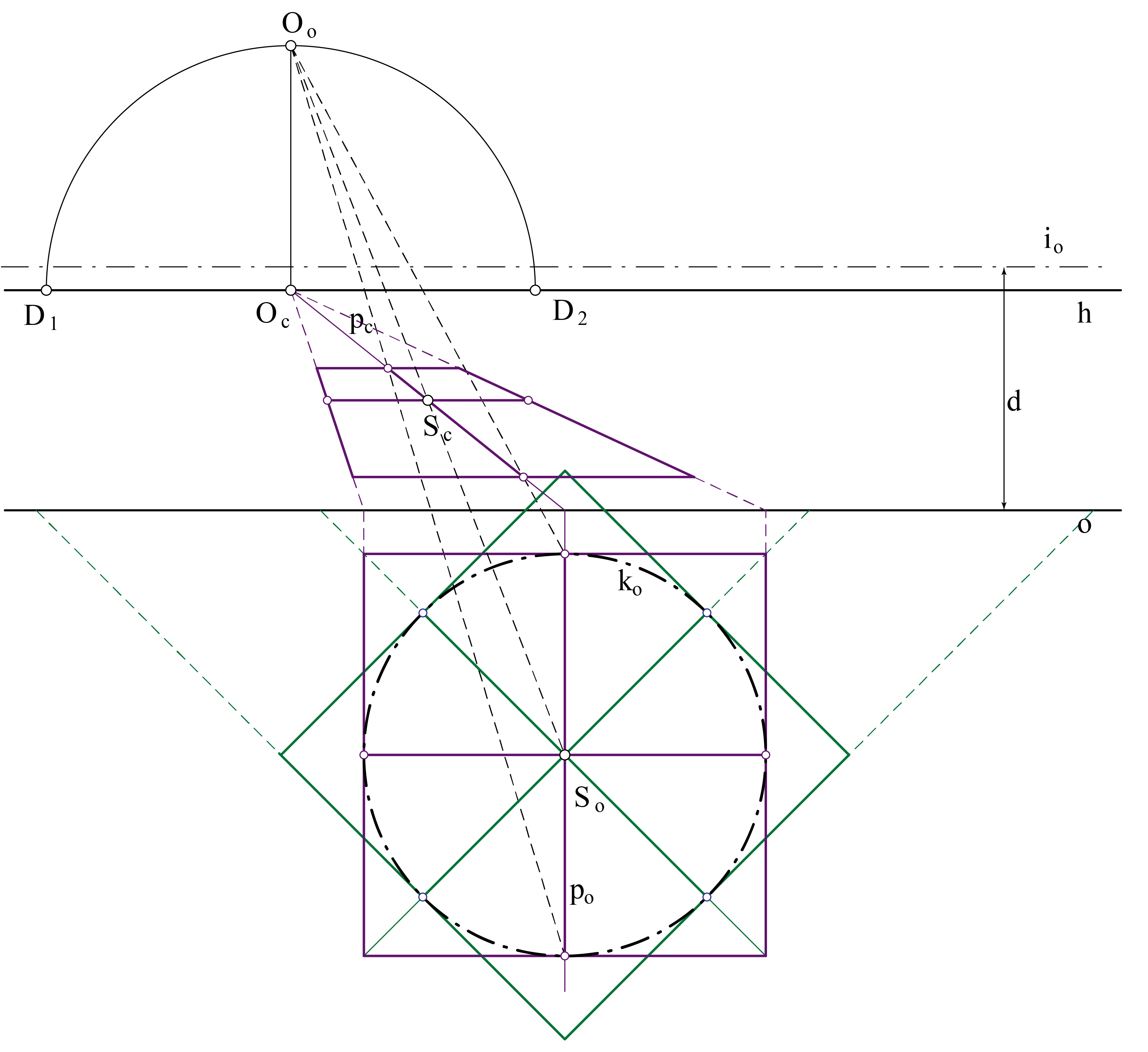
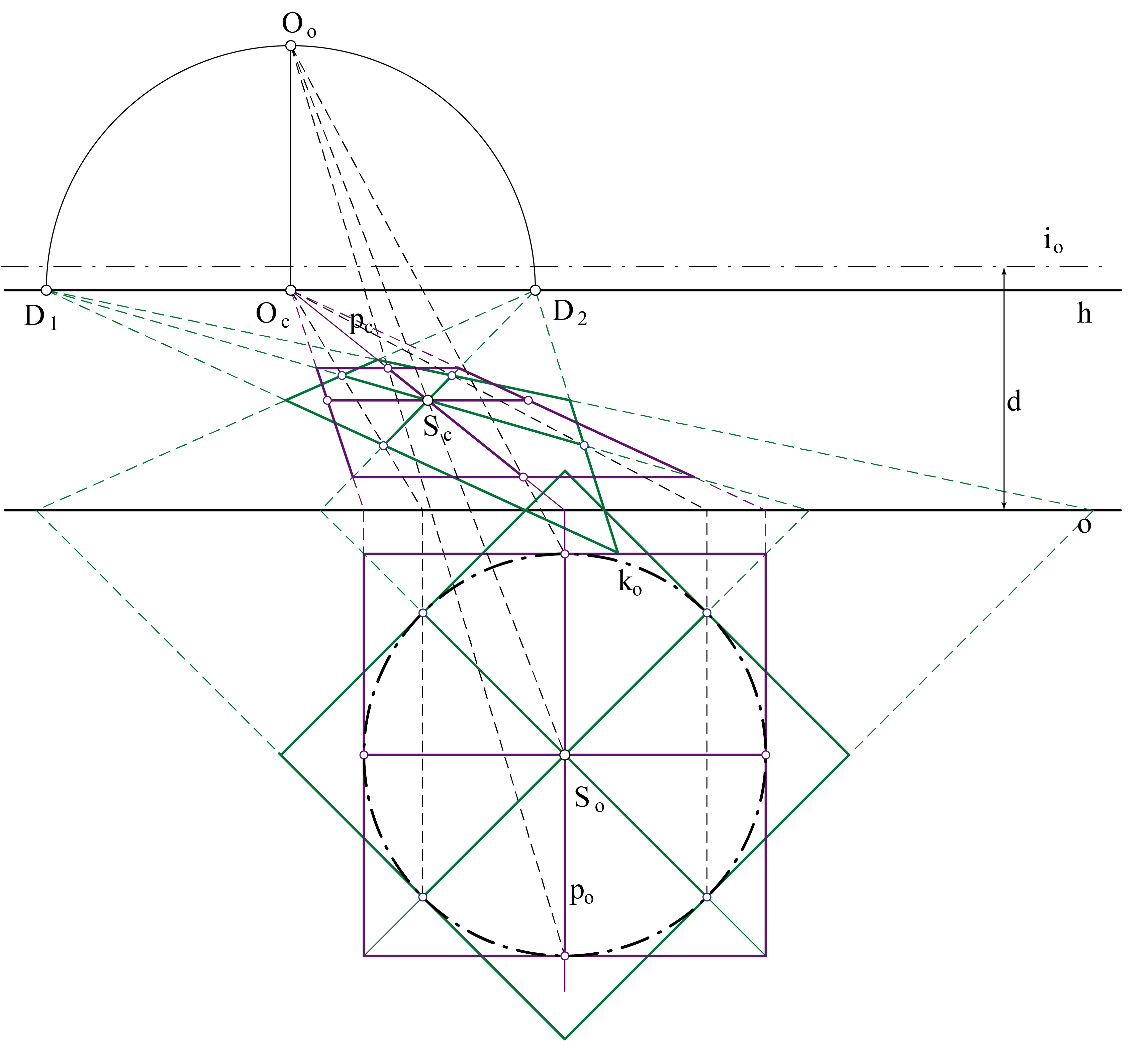
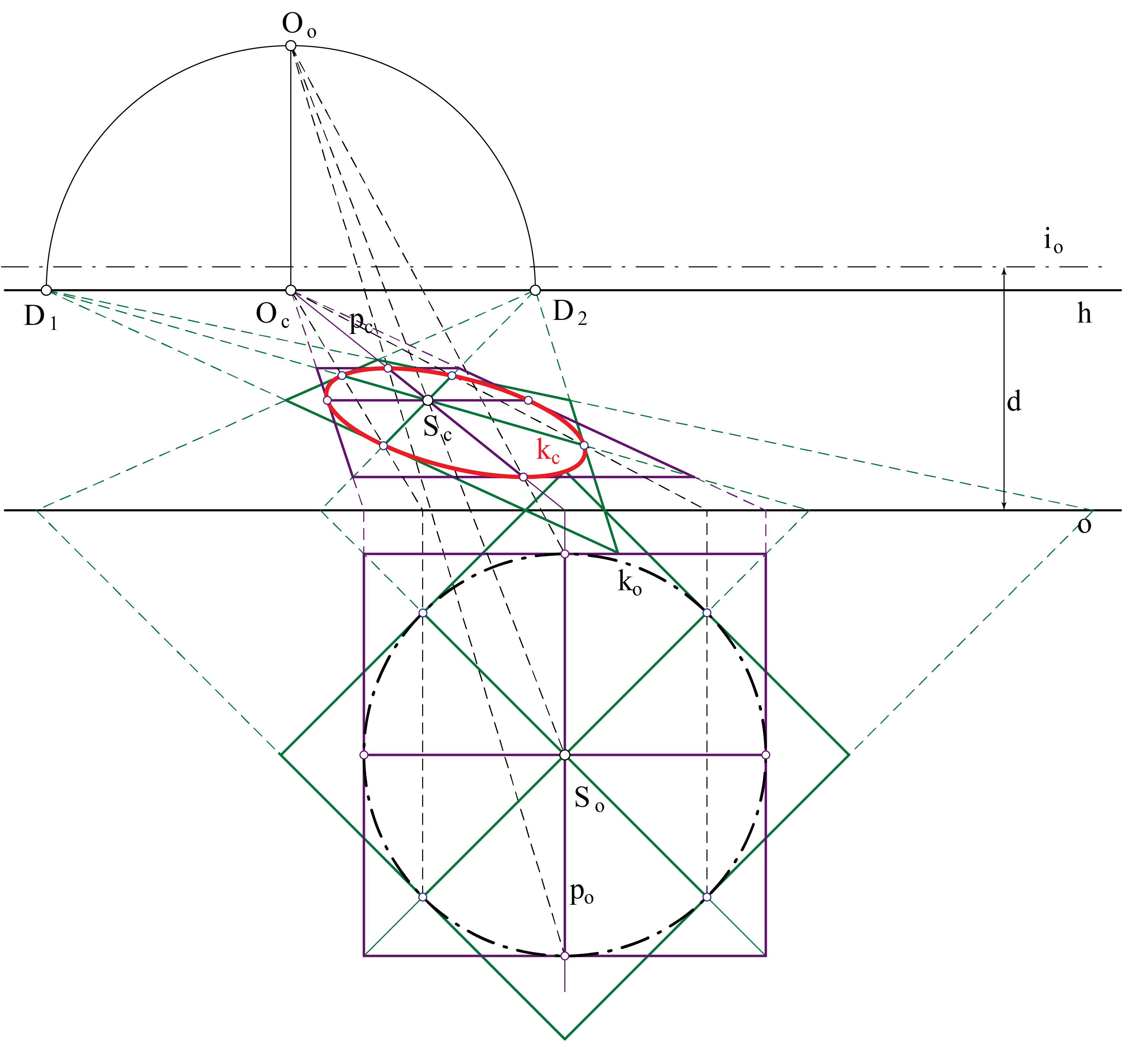
- Konstruiramo točku \(\small O_\circ\) i izbježnicu \(\small i_\circ .\) Zaključujemo da je \(\small k_c\) elipsa
- Uočimo pravac \(\small p_\circ\) kroz \(\small S_\circ\) (\(\small p\) je okomit na ravninu slike) i konstruiramo njegovu sliku \(\small p_c\)
- Koristeći svojstvo perspektivne kolineacije, konstruiramo sliku središta kružnice i onog njezinog promjera koji leži na pravcu \(\small p\). Uočite da se promjeri kružnice ne projiciraju u promjere njezine slike
- Pomoću perspektivne kolineacije odredimo slike za još tri promjera kružnice \(\small k\) (onog paralelnog s ravninom slike i dva koji ju sijeku pod kutom od \(\small 45^\circ\)) kao i slike tangenata u krajnjim točkama tih promjera
- Iscrtamo elipsu \(\small k_c\) pomoću osam točaka u kojima imamo tangente