Hiperbolički paraboloid (HIPAR)

Bilo koja tri mimosmjerna pravca koji su paralelni s istom ravninom ravnalice su hiperboličkog paraboloida. Njihove transverzale čine izvodnice jednog sustava. Ravninu s kojom su ravnalice paralelne nazivamo direkcijska ravnina hipara.

Za sustave izvodnica ove plohe vrijede ista svojstva kao i kod jednokrilnog hiperboloida:
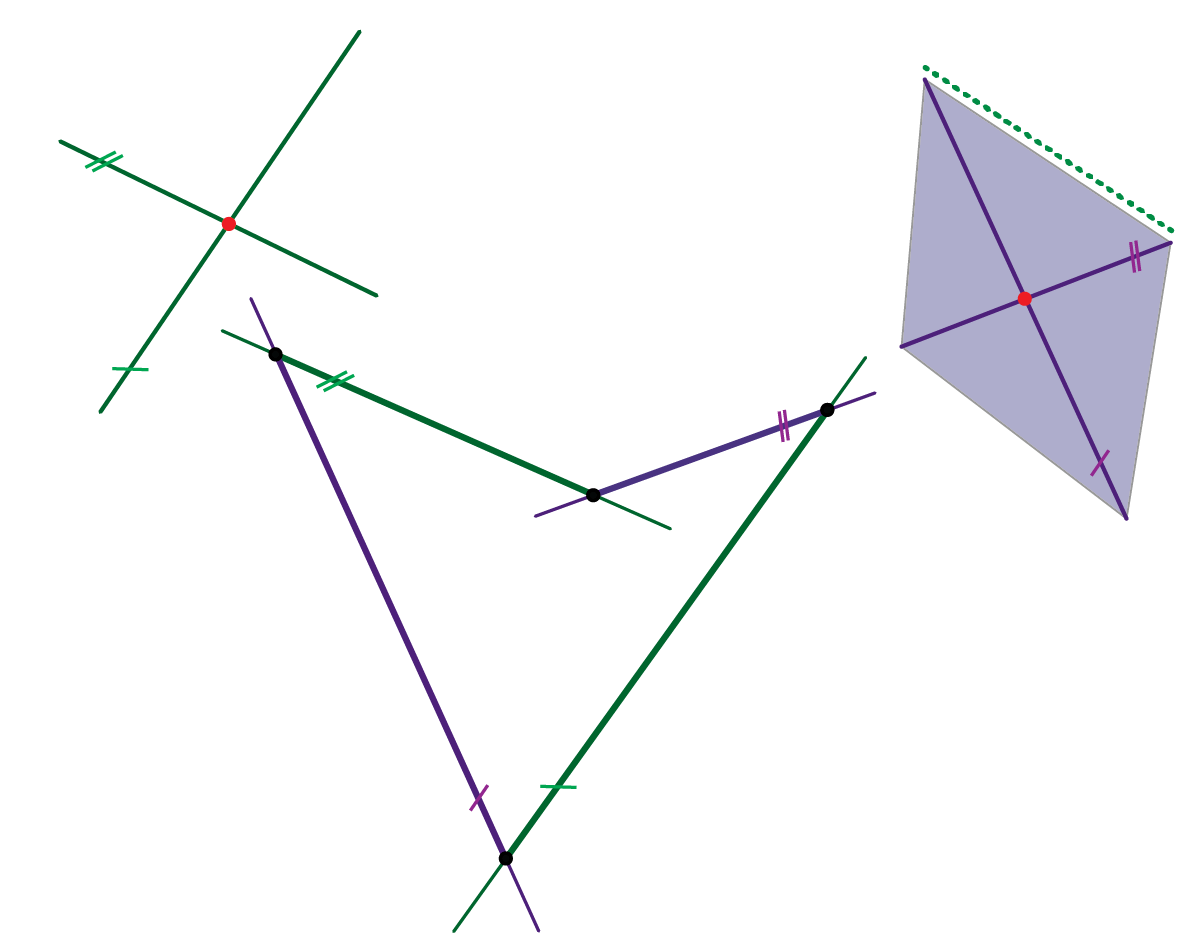
  • Hipar ima dva sustava izvodnica, odnosno svakom njegovom točkom prolaze dvije izvodnice - svaka iz jednog sustava.
  • Sve izvodnice istog sustava međusobno su mimosmjerne, a svaka od njih siječe sve izvodnice drugog sustava.
  • Bilo koje tri izvodnice jednog sustava možemo odabrati za ravnalice hipara.

Međutim, hipar ima i neka posebna svojstva:
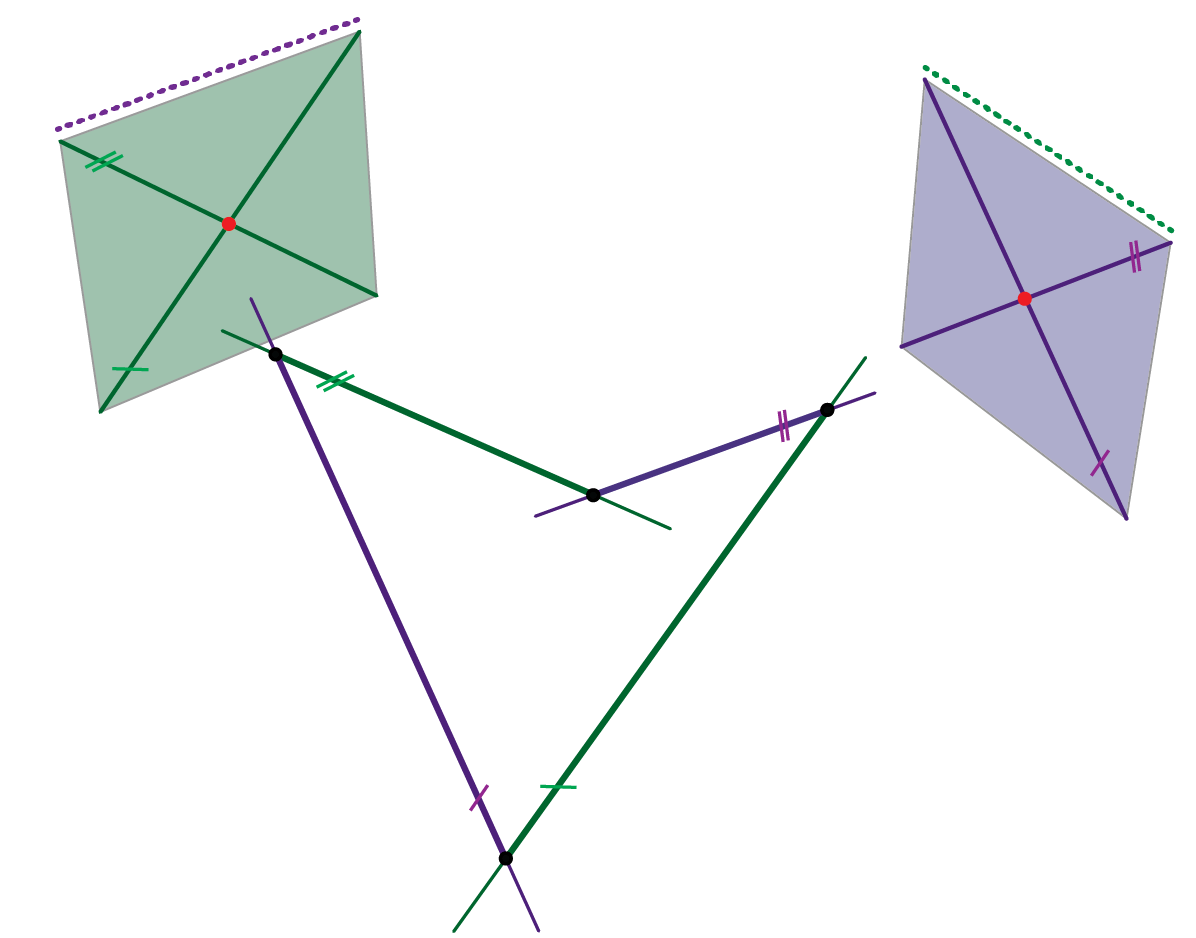
  • Sve izvodnice jednog sustava paralelne su s istom direkcijskom ravninom.
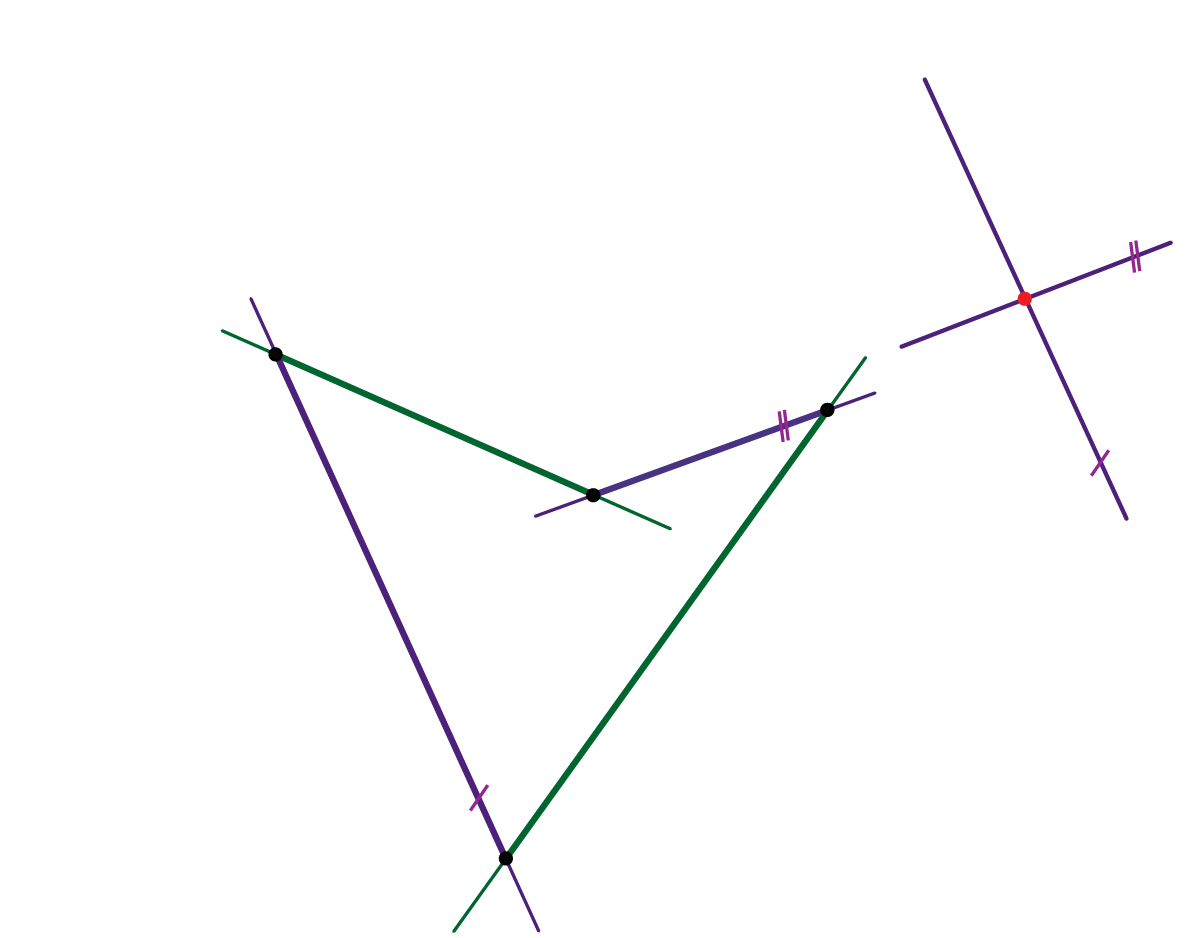
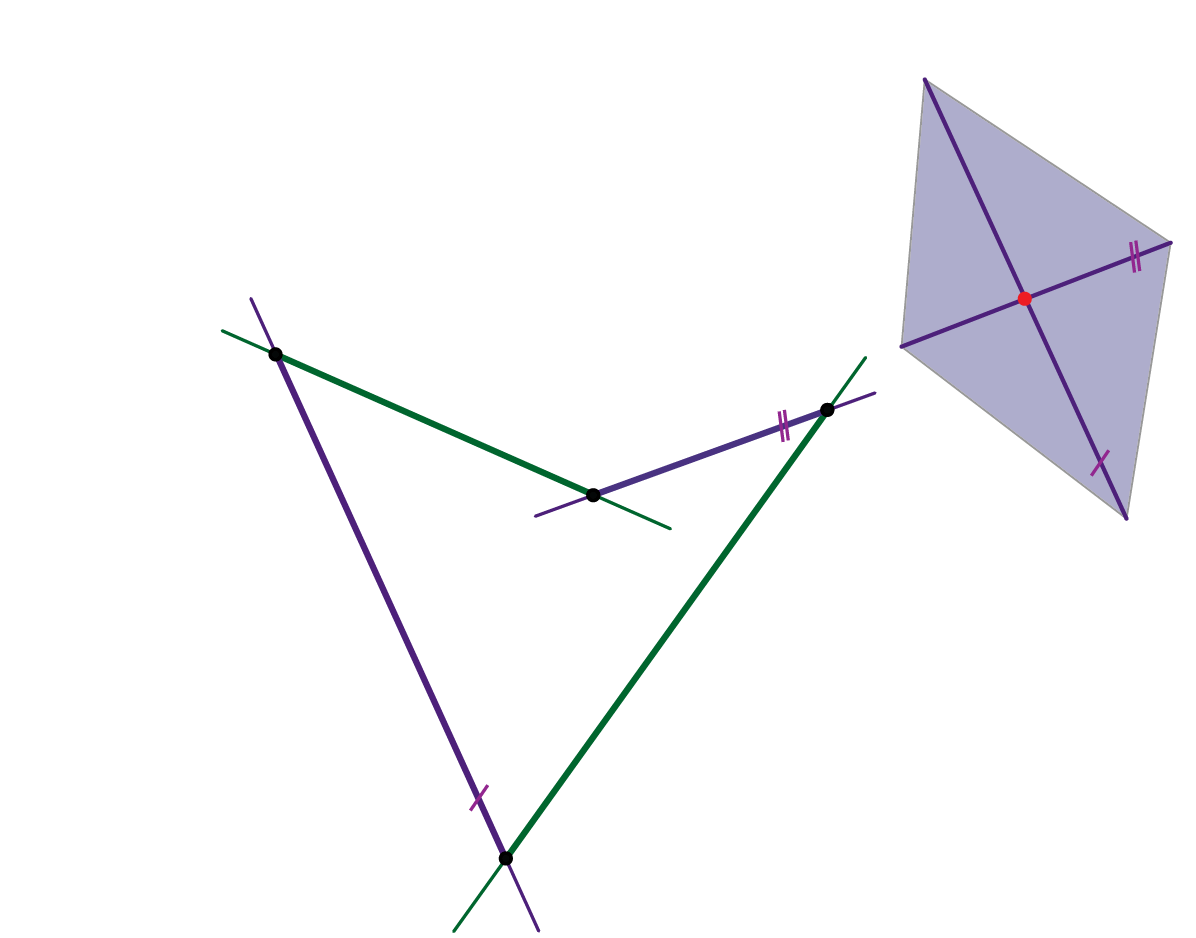
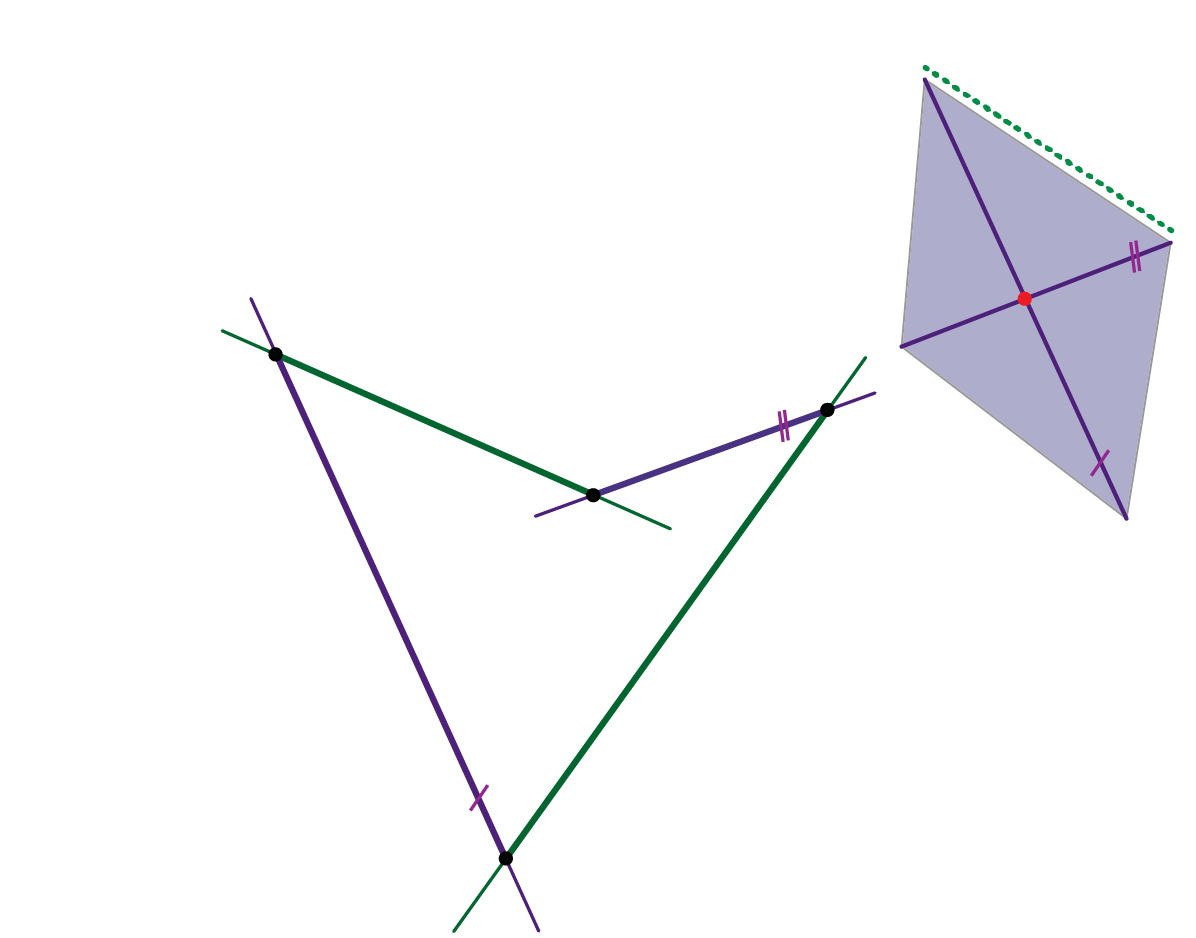
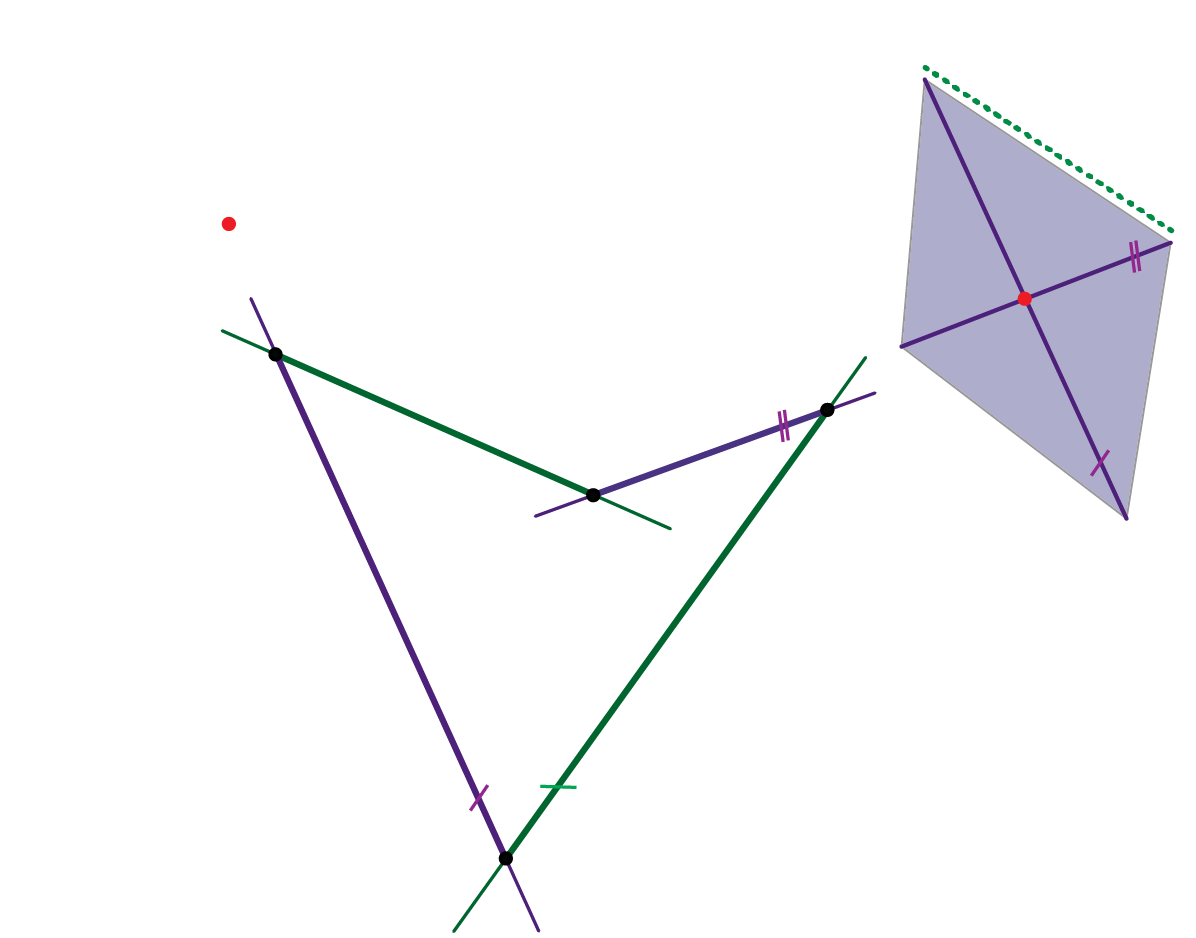
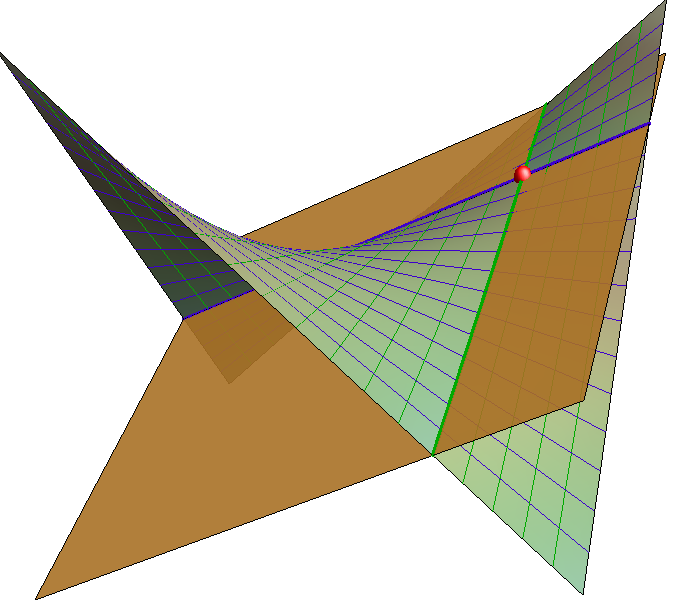
  • U svakom sustavu izvodnica hipara postoji jedna izvodnica koja je beskonačno daleka - to je beskonačno daleki pravac direkcijske ravnine drugog sustava (vidi sliku 430).
  • Hipar je konoid 2. stupnja.

Slika 430


Tri načina zadavanja hiperboličkog paraboloida kao pravčaste plohe

1. Ravnalice plohe su tri mimosmjerna pravca koji su paralelni s istom ravninom. Bilo koje tri izvodnice istog sustava mogu se odabrati za ravnalice plohe. Svakom točkom bilo koje od te tri ravnalice prolazi jedinstvena transverzala drugih dviju - to je izvodnica drugog sustava (vidi animacije 77 i 78).


Animacija 77
Animacija 78

2. Ravnalice plohe su tri mimosmjerna pravca od kojih je jedan u beskonačnosti. Ta beskonačno daleka ravnalica zadana je direkcijskom ravninom. Izvodnice drugog sustava konstruiramo kao spojnice probodišta zadanih ravnalica sa sustavom paralelnih direkcijskih ravnina (vidi animacije 79 i 80).

Animacija 79
Animacija 80

3. Hipar je zadan vitoperim (prostornim) četverovrhom čije stranice leže na četiri njegove izvodnice (po dvije iz svakog sustava). Na temlju tako zadanih elemenata moguće je za svaki sustav izvodnica odrediti direkcijsku ravninu (vidi prezentaciju 82), a zatim i konstruirati po volji mnogo izvodnica hipara (vidi animaciju 81).



Prezenacija 82
Animacija 81

Presjeci hipara ravninom

Svaka dirna ravnina hiperboličkog paraboloida siječe tu plohu po dva pravca, odnosno po izvodnicama hipara koje prolaze diralištem (vidi sliku 431). Beskonačno daleka ravnina prostora također je dirna ravnina hiperboličkog paraboloida koja sadrži njegove dvije beskonačno daleke izvodnice. Njezino je diralište beskonačno daleka točka presječnice direkcijskih ravnina hipara (vidi sliku 432).
Slika 431 Slika 432


Ako ravnina nije dirna ravnina hipara, njezin presjek s tom plohom je prava krivulja 2. stupnja koja nikada nije elipsa. Naime, bilo koja ravnina prostora siječe beskonačcno daleke izvodnice hipara u realnim točkama pa će presjek biti parabola, ako je ravnina paralelna s presječnicom direkcijskih ravnina (vidi sliku 433), a hiperbola u svim ostalim slučajevima (slika 434).
Slika 433 Slika 434

Hipar kao translacijska (klizna) ploha

Kao što smo već naveli, hiperbolički je paraboloid translacijska ploha. Nastaje translatornim gibanjem (klizanjem) parabole po parabaoli pri čemu su grane parabola okrenute na suprotne strane (vidi animaciju 82).

Animacija 82

Slika 435: Hipar s iscrtanim sustavom parabola (gore) i pravaca (dolje)



Sonja Gorjanc - PERSPEKTIVA (predavanja)