Hiperboloidi

Osnovna podjela hiperboloida je na dvokrilne (dvodijelne) i jednokrilne (jednodijelne), a svaki od ta dva tipa dijeli se nadalje na eliptičke i rotacijske (kružne). Sve točke na dvokrilnim hiperboloidima su eliptičke, a one na jednokrilnima su hiperboličke. Realni presjeci ovih ploha mogu biti sve prave konike (elipse, kružnice, parabole i hiperbole), a u slučaju jednokrilnog hiperboloida i dva realna pravca. Beskonačno daleka ravnina prostora siječe hiperboloide po realnim konikama.

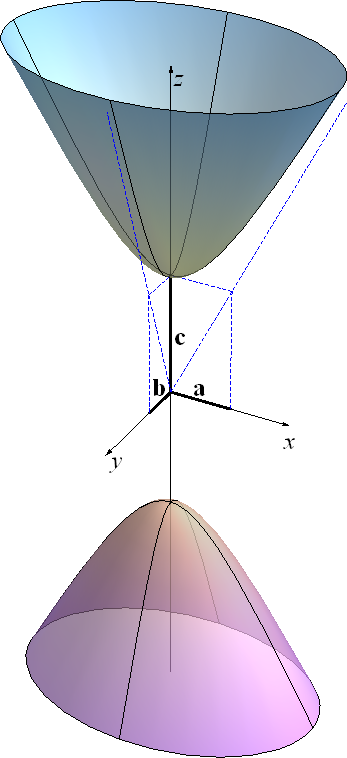
1. dvokrilni hiperboloidi

\(-\frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\) (eliptički)

\(-\frac{x^2+y^2}{a^2}+\frac{z^2}{c^2}=1\) (rotacijski)

Nastaje rotacijom hiperbole oko njezine realne osi (slika 328).

Slika 327: Dvokrilni eliptički hiperboloid

Slika 328

Animacija 21: Dvokrilni rotacijski hiperboloid

2. jednokrilni hiperboloidi

\(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1\) (eliptički)

Jednokrilni hiperboloid je pravčasta ploha s dva sustava izvodnica, odnosno svakom točkom te plohe prolaze dva pravca koji leže na toj plohi (vidi sliku 330).

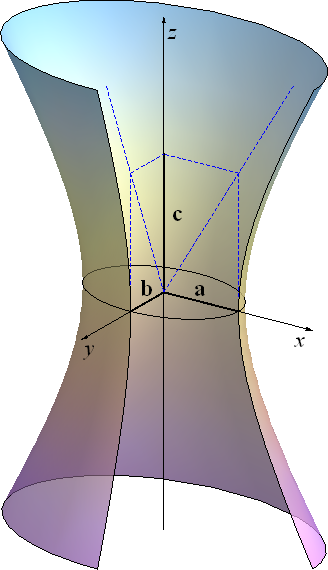
Slika 329: Jednokrilni eliptički hiperboloid

Slika 330: Jednokrilni eliptički hiperboloid je pravčasta ploha

\(\frac{x^2}{a^2+y^2}-\frac{z^2}{c^2}=1\) (rotacijski)

Ova ploha nastaje na dva načina:

Rotacijom hiperbole oko njene imaginarne osi (slika 331 i animacija 22).


Slika 331	Animacija 22

Rotacijom pravca oko osi s kojom je taj pravac mimosmjeran (animacije 23 i 24).
Pravac koji rotira je izvodnica koja pripada bilo kojem od dva sistema izvodnica ove plohe.

Animacija 23

Animacija 24

Studentima, koje zanima nešto više o pravčastim hiperboloidima, preporučujemo sljedeći odjeljak.

Sonja Gorjanc - GeomTeh3D - Razvojni projekt Sveučiliša u Zagrebu