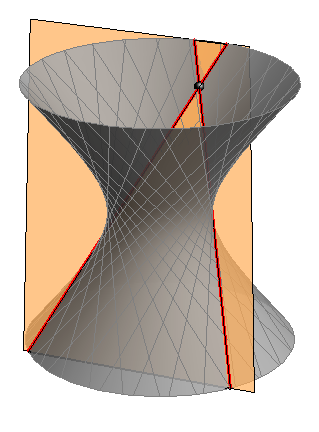
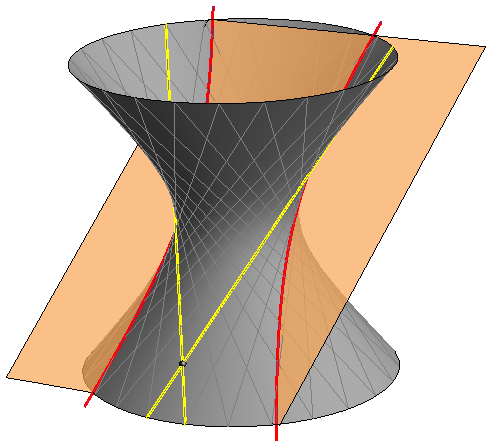
Jednokrilni (jednodijelni) hiperboloid

  • Bilo koja tri mimosmjerna pravca koji nisu paralelni s istom ravninom ravnalice su jednokrilnog hiperboloida. Njihove transverzale čine izvodnice jednog sustava.

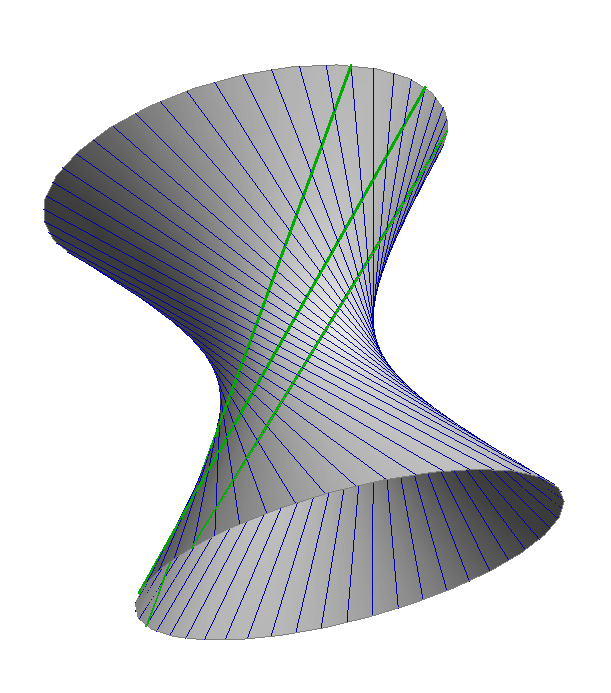
  • Jednokrilni hiperboloid ima dva sustava izvodnica, odnosno svakom njegovom točkom prolaze dvije izvodnice, svaka iz jednog sustava.

  • Sve izvodnice istog sustava međusobno su mimosmjerne, a svaka od njih siječe sve izvodnice drugog sustava.

  • Bilo koje tri izvodnice jednog sustava možemo odabrati za ravnalice jednokrilnog hiperboloida.
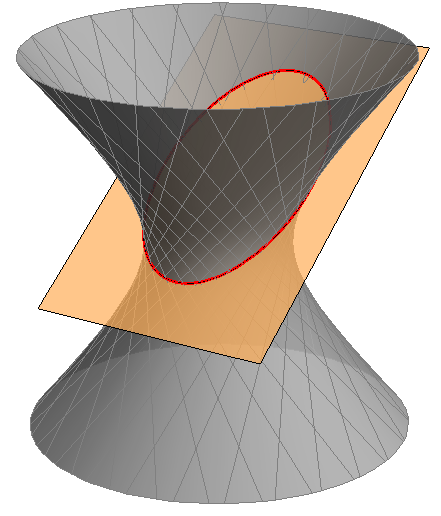
Animacije 70 i 71 te slike 422 i 423 ilustriraju navedena svojstva.
Animacija 70 Slika 422 Animacija 71 Slika 423

Presjeci jednokrilnog hiperboloida

U svakoj točki jednokrilnog hiperboloida dirna je ravnina određena dvjema izvodnicama koje se u njoj sijeku (slika 424).

Osim dviju izvodnica presjek jednokrilnog hiperboloida može biti:
hiperbola \(-\) ako je presječna ravnina paralelna s dvije njegove ukrštene izvodnice (slika 425)
parabola \(-\) ako je presječna ravnina paralelna s dvije njegove paralelne izvodnice (slika 426)
elipsa \(-\) ako presječna ravnina nije paralelna niti s jednom njegovom izvodnicom (slika 427).

Slika 424 Slika 425 Slika 426 Slika 427

Rotacijski jednokrilni hiperboloid

Jednodijelni rotacijski hiperboloid izvodimo na dva načina:

Animacija 72

Animacija 73

Animacija 74 		Za svaki od dva sustava izvodnica ovog hiperboloida vrijedi da je dobiven rotacijom bilo koje svoje izvodnice oko osi hiperboloida. Vidi animacije 74 i 75.







Animacija 75

Grlena kružnica

Paralelu najmanjeg polumjera nazivamo grlenom kružnicom rotacijskog jednodijelnog hiperboloida (slika 428). Na toj kružnici leže tjemena svih meridijanskih hiperbola plohe. Njezin je polumjer jednak udaljenosti bilo koje izvodnice od osi hiperboloida.

Projekcije izvodnica takvog hiperboloida na ravninu njegove grlene kružnice (ili na neku s njom paralelnu) su tangente grlene kružnice, vidi sliku 429.
Slika 428 Slika 429

Asimptotski stožac

Asimptote svih meridijanskih hiperbola jednokrilnog rotacijskog hiperboloida izvodnice su rotacijskog stošca kojem je vrh u središtu grlene kružnice, vidi animaciju 76. Taj stožac nazivamo asimptotskim stošcem hiperboloida. Hiperboloid i njegov asimptotski stožac dodiruju se duž jedne konike u beskonačno dalekoj ravnini.

Svaka ravnina, koja nije dirna za rotacijski hiperboloid i koja ne prolazi vrhom njegovog asimptotskog stošca, siječe hiperboloid i njegov asimptotski stožac po istoj vrsti konike.








Animacija 76


Sonja Gorjanc - PERSPEKTIVA (predavanja)