




Next: Analitičke i harmonijske funkcije
Up: Funkcije kompleksne varijable
Previous: Pojam funkcije kompleksne varijable
Contents
Index
Subsections
Primjer 7.4
Funkcija 
se definira formulom
i zove se
eksponencijalna funkcija kompleksne varijable. Iz ove
definicije, uz pomoć adicijskih teorema za sinus i kosinus, slijedi
važno svojstvo eksponencijalne funkcije
Navedimo neka svojstva te funkcije.
a) Iz formule slijedi
Za

imamo
 |
(7.1) |
To je poznata
Eulerova formula. Odatle
Tako je
b) Jednadžba
nema rješenja, jer je

za svaki

c) Neka je
 i neka je
i neka je
 Jednadžba
Jednadžba
se svodi na
odakle slijedi
Iz ovih formula se
vidi da je slika funkcije

cijeli skup

Pri tom
se uočava da se pruga

preslikava na

Na isti skup se preslikavaju i pruge

Tako funkcija

lijepi beskonačno mnogo točaka u jednu točku.
Iz
slijedi
pa se radi o zrakama u

-ravnini

gdje je

pa se radi o kružnicama u

-ravnini

gdje je

Tako imamo sljedeću sliku
Primjer 7.5
Funkcija 
Iz prethodnog primjera se vidi da ne postoji inverzna funkcija od funkcije
 No, ako uzmemo restrikciju funkcije
No, ako uzmemo restrikciju funkcije  na skup
na skup
onda je preslikavanje

injekcija, i prema tome postoji inverzna funkcija. Ona
je definirana na

a formula se dobije iz zahtjeva
Slijedi
tj.
Ova funkcija se zove
 -ta grana prirodnog logaritma
-ta grana prirodnog logaritma. Nulta grana
prirodnog logaritma
Ln

se obično zove
glavna vrijednost (grana) prirodnog logaritma.
Iz
slijedi da glavna grana prirodnog logaritma preslikava koordinatne
linije u  -ravnini u krivulje čije su jednadžbe dane formulama
Ovim jednadžbama su dane krivulje u
-ravnini u krivulje čije su jednadžbe dane formulama
Ovim jednadžbama su dane krivulje u  -ravnini.
Te krivulje vidimo na sljedećoj slici
-ravnini.
Te krivulje vidimo na sljedećoj slici
Primjer 7.6
 -ti korijen
-ti korijen. U Matematici I smo prodiskutirali

-ti
korijen kompleksnog broja

i došli do formule

To pokazuje da se, ukoliko želimo imati

-ti
korijen kao funkciju, moramo odlučiti za jednu od vrijednosti broja

Tako i

-ti korijen ima više grana. Ona, koja se dobije kad se uzme

se zove
glavna grana  -tog korijena
-tog korijena.
Kako djeluje funkcija 'treći korijen' vidi se na sljedećim slikama.
Tu smo kao koordinatne linije u  -ravnini uzeli koordinatne linije u
polarnom sustavu.
-ravnini uzeli koordinatne linije u
polarnom sustavu.
Primjer 7.7
Trigonometrijske funkcije.
Iz formula
slijedi
Shodno tome definiramo trigonometrijske funkcije na

kako slijedi
Na temelju ovih definicija i svojstava kompleksne eksponencijalne funkcije,
lako se može pokazati da vrijede poznate formule, kao što su adicijski
teoremi, Pitagorin poučak, formule za dvostruki argument, polovični
argument i sl.
Kako djeluju te funkcije vidi se iz sljedećih slika.
Sinus:
pa za  imamo
dok za
imamo
dok za  imamo
Kosinus:
pa za
imamo
Kosinus:
pa za  imamo
dok za
imamo
dok za  imamo
Tangens:
pa za
imamo
Tangens:
pa za  imamo
dok za
imamo
dok za  imamo
Kotangens:
pa za
imamo
Kotangens:
pa za  imamo
dok za
imamo
dok za  imamo
imamo
Primjer 7.8
Hiperbolne funkcije.
Hiperbolne funkcije se definiraju kao i u realnom području
Također i za hiperbolne funkcije vrijede formule poznate iz realnog
područja. Tako na pr.
Iz gornjih formula slijede i veze između trigonometrijskih i hiperbolnih funkcija
Kako djeluju te funkcije vidi se iz sljedećih slika
Sinus hiperbolni:
Odatle
Kosinus hiperbolni:
Odatle
Tangens hiperbolni:
Odatle
Kotangens hiperbolni:
Odatle
Primjer 7.9
Opća potencija

Definirana je formulom
Primjer 7.10
Arcus i area funkcije.
Tako je
Analogno se mogu dobiti formule za ostale arcus, kao i za area funkcije.
Definicija 48
Za funkciju

gdje je

područje u

kažemo da je
neprekidna u točki 
ako

postoji

tako da
Ako je
funkcija neprekidna u svakoj točki iz

onda kažemo da je
neprekidna na 
. U protivnom kažemo da ima
prekid na

.
Slika 7.3:
Neprekidnost funkcije kompleksne varijable.
|
|
Vrijedi
- -
- Funkcija
 je neprekidna u točki
je neprekidna u točki  ako i samo ako su funkcije
ako i samo ako su funkcije  neprekidne u točki
neprekidne u točki 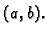
- -
- Neka je
 neprekidna u točki
neprekidna u točki
 Tada postoje
Tada postoje  i
i  takvi da
takvi da
- -
- Neka je
 neprekidna u točki
neprekidna u točki
 i neka je
i neka je
 Tada postoji
Tada postoji  takav da
takav da
- -
- Neka je
 gdje su
gdje su  područja takva da je
područja takva da je
 Neka je
Neka je  neprekidna u točki
neprekidna u točki
 a
a  neprekidna u točki
neprekidna u točki  Tada je funkcija
Tada je funkcija
 neprekidna u točki
neprekidna u točki 
- -
- Neka su
 i
i
 funkcije neprekidne u točki
funkcije neprekidne u točki  i neka je
i neka je
 Tada je
Tada je
- 1.
 neprekidna u točki
neprekidna u točki 
- 2.
 neprekidna u točki
neprekidna u točki 
- 3.
 neprekidna u točki
neprekidna u točki 
- 4.
- Ako je
 onda je
onda je
 neprekidna u točki
neprekidna u točki 
- -
- Neka je
 konvergentan niz kompleksnih brojeva i neka je
konvergentan niz kompleksnih brojeva i neka je
 Neka je
Neka je
 neprekidna funkcija, i neka je
neprekidna funkcija, i neka je
 Tada
je kompozicija
Tada
je kompozicija
 konvergentan niz i vrijedi
konvergentan niz i vrijedi
- -
- Ako je funkcija neprekidna na zatvorenom ograničenom skupu
 onda je ona ograničena na
onda je ona ograničena na 
- -
- Ako je funkcija neprekidna na zatvorenom ograničenom skupu
 onda postoje
onda postoje
 takvi da je
takvi da je
Definicija 49
Kažemo da funkcija

definirana na području

osim možda u
točki

ima
limes 
u točki

ako

postoji

tako da
Pišemo

Vrijedi
- -
- Ako funkcija nije definirana
u točki
 a ima limes
a ima limes  u točki
u točki  i ako stavimo
i ako stavimo
 za
za  i
i
 onda je
onda je  neprekidna u točki
neprekidna u točki

- -
- Ako je funkcija definirana u točki
 ima limes
ima limes  u točki
u točki  koji možda
nije jednak
koji možda
nije jednak  i ako stavimo
i ako stavimo
 za
za  i
i
 onda je
onda je  neprekidna u točki
neprekidna u točki 
- -
-
 ako i samo ako vrijedi
ako i samo ako vrijedi
- -
- Neka je
 neprekidna funkcija u točki
neprekidna funkcija u točki  Tada
Tada  ima limes u točki
ima limes u točki  i
i

- -
- Neka
 ima limes u točki
ima limes u točki  i neka je
i neka je
 Tada je
Tada je  neprekidna u točki
neprekidna u točki 
Definicija 50
Neka je

područje u

Kažemo da je funkcija
 derivabilna u točki
derivabilna u točki 
ako postoji
Taj broj označavamo s

i zovemo
derivacijom funkcije  u točki
u točki 
.
Također se umjesto  može pisati i
može pisati i

Primjer 7.11
Funkcija

je derivabilna na

i

Rješenje. Neka je  proizvoljan kompleksan broj.
proizvoljan kompleksan broj.
Primjer 7.12
Funkcija

nije derivabilna u točki

Rješenje. Limes, koji se pojavljuje u definiciji derivacije funkcije
kompleksne varijable, ne ovisi o putu u Gaussovoj ravnini kojim  teži prema nuli. Po svakom putu mora postojati limes i uvijek mora biti jedan te isti broj. Izaberimo najprije put duž kojeg je
teži prema nuli. Po svakom putu mora postojati limes i uvijek mora biti jedan te isti broj. Izaberimo najprije put duž kojeg je  Tada je
Tada je
Po drugom putu na kojem je

imamo
Budući da limesi nisu isti, zaključujemo
da funkcija nije derivabilna u točki

Ako je funkcija  derivabilna u svakoj točki područja
derivabilna u svakoj točki područja  onda
funkciju
onda
funkciju  koja kompleksnom broju
koja kompleksnom broju  pridružuje
pridružuje  zovemo
derivacijom funkcije
zovemo
derivacijom funkcije  .
.
Kao i kod derivacija realnih funkcija realne varijable, imamo formule
- 1.
- Nabrojite osnovne elementarne funkcije. Kako se definiraju? U čemu je
problem pri definiranju na pr. logaritma?
- 2.
- Kojim formulama se definiraju arcus funkcije?
- 3.
- Kad kažemo da je funkcija kompleksne varijable neprekidna?
- 4.
- Kako se neprekidnost odnosi prema operacijama s funkcijama?
- 5.
- Kako definiramo limes funkcije kompleksne varijable i koja
svojstva ima?
- 1.
- Dokazati sljedeće formule
- (a)
-

- (b)
-

Rješenje.
- (a)
- Pomoću adicionog teorema za

- (b)
- Također pomoću adicionog teorema ali za
 Odatle
Koristeći formule
Odatle
Koristeći formule
 i
i
 imamo
imamo
- 2.
- Odrediti one točke
 u kojima funkcija
u kojima funkcija
 prima realne
vrijednosti.
prima realne
vrijednosti.
Rješenje. Funkcija
 prima realne vrijednosti u onim točkama
kompleksne ravnine, u kojima se njezin imaginarni dio
prima realne vrijednosti u onim točkama
kompleksne ravnine, u kojima se njezin imaginarni dio  poništava.
poništava.
Odatle
 i
i
 Ovdje je važno napomenuti da su
Ovdje je važno napomenuti da su  i
i
 realne varijable. Iz jednadžbe slijedi
realne varijable. Iz jednadžbe slijedi
 a iz nejednadžbe slijedi da treba isključiti točku
a iz nejednadžbe slijedi da treba isključiti točku  Dakle, to je skup točaka na pravcima
Dakle, to je skup točaka na pravcima
 paralelnim s realnom osi, osim ishodišta.
paralelnim s realnom osi, osim ishodišta.
- 3.
- Riješiti jednadžbu

Rješenje. Jedan od načina rješavanja je da izjednačimo realne i
imaginarne dijelove s lijeva i s desna, i tako dobijemo dvije
jednadžbe za nepoznanice  i
i  Ovdje, međutim, možemo
koristiti formulu za inverznu funkciju
Ovdje, međutim, možemo
koristiti formulu za inverznu funkciju
 Dakle
Dakle
Imamo
pa
daje dvije vrijednosti
Prva vrijednost daje rješenja
a druga





Next: Analitičke i harmonijske funkcije
Up: Funkcije kompleksne varijable
Previous: Pojam funkcije kompleksne varijable
Contents
Index
Salih Suljagic
2000-03-11
![]() i neka je
i neka je
![]() Jednadžba
Jednadžba

![]() i neka je
i neka je
![]() Jednadžba
Jednadžba

![]() No, ako uzmemo restrikciju funkcije
No, ako uzmemo restrikciju funkcije ![]() na skup
na skup

![% latex2html id marker 44602
$\displaystyle \sqrt[n]{z}= \sqrt[n]{\vert z\vert} ...
...k\pi}{n}\right)=
\sqrt[n]{\vert z\vert}\,e^{i\,\frac{ {\rm Arg\,}z +2k\pi}{n}},$](img3310.gif)
![]() -ravnini uzeli koordinatne linije u
polarnom sustavu.
-ravnini uzeli koordinatne linije u
polarnom sustavu.























![]() može pisati i
može pisati i

![]() proizvoljan kompleksan broj.
proizvoljan kompleksan broj.

![]() teži prema nuli. Po svakom putu mora postojati limes i uvijek mora biti jedan te isti broj. Izaberimo najprije put duž kojeg je
teži prema nuli. Po svakom putu mora postojati limes i uvijek mora biti jedan te isti broj. Izaberimo najprije put duž kojeg je ![]() Tada je
Tada je


![]() derivabilna u svakoj točki područja
derivabilna u svakoj točki područja ![]() onda
funkciju
onda
funkciju ![]() koja kompleksnom broju
koja kompleksnom broju ![]() pridružuje
pridružuje ![]() zovemo
derivacijom funkcije
zovemo
derivacijom funkcije ![]() .
.




![]() prima realne vrijednosti u onim točkama
kompleksne ravnine, u kojima se njezin imaginarni dio
prima realne vrijednosti u onim točkama
kompleksne ravnine, u kojima se njezin imaginarni dio ![]() poništava.
poništava.

![]() i
i ![]() Ovdje, međutim, možemo
koristiti formulu za inverznu funkciju
Ovdje, međutim, možemo
koristiti formulu za inverznu funkciju
![]() Dakle
Dakle
![% latex2html id marker 45104
$\displaystyle {\rm Arccos}\,\frac{1}{4}\,(3+i) = \...
...left[i\,\frac{1}{4}\,(3+i) +
\sqrt{1-\left(\frac{1}{4}\,(3+i)\right)^2}\right].$](img3448.gif)




