




Next: Krivulje i krivuljni integrali
Up: Višestruki integrali
Previous: Računanje integrala supstitucijom
Contents
Index
Subsections
Neka je dano  materijalnih točaka s masama
materijalnih točaka s masama
 u
prostoru tako da su njihovi radijvektori
u
prostoru tako da su njihovi radijvektori
 Točka
Točka  čiji je
radijvektor
čiji je
radijvektor  sa svojstvom da je
sa svojstvom da je
 |
(2.5) |
zove se središte masa
 Središte masa ima sljedeće važno
svojstvo. Pretpostavimo da se materijalne točke
Središte masa ima sljedeće važno
svojstvo. Pretpostavimo da se materijalne točke
 gibaju. Tada su njihovi radijvektori
gibaju. Tada su njihovi radijvektori
 funkcije
vremena. Središte masa se također giba. Pripadni radijvektor je
funkcije
vremena. Središte masa se također giba. Pripadni radijvektor je
 Ako (2.5) deriviramo po vremenu
Ako (2.5) deriviramo po vremenu  i tu
derivaciju označimo s točkom kao što je uobičajeno, slijedi
i tu
derivaciju označimo s točkom kao što je uobičajeno, slijedi
 |
(2.6) |
Prema tome količina gibanja sustava materijalnih točaka jednaka je
količini gibanja jedne materijalne točke čija je masa jednaka
ukupnoj masi sustava, a nalazi se u središtu masa sustava.
Nađimo sada koordinate središta masa. Stavimo, radi kratkoće
zapisa,
i pretpostavimo da je
Tada iz (2.5) slijedi
Neka je dano materijalno tijelo T, sa zadanom gustoćom mase
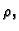 koje zauzima u prostoru neko zatvoreno područje
koje zauzima u prostoru neko zatvoreno područje
 Želimo naći središte masa tijela
Želimo naći središte masa tijela  U tu svrhu opišemo
oko tijela minimalni kvadar
U tu svrhu opišemo
oko tijela minimalni kvadar  stranica paralelnih koordinatnim ravninama,
i definiramo gustoću mase na kvadru
stranica paralelnih koordinatnim ravninama,
i definiramo gustoću mase na kvadru 
Subdivizijama podijelimo  na male kvadre
na male kvadre  U svakom od
njih izaberemo jednu točku
U svakom od
njih izaberemo jednu točku
 Zamislimo da
je masa malog kvadra
Zamislimo da
je masa malog kvadra  koncentrirana u toj točki. Ona je
približno jednaka
koncentrirana u toj točki. Ona je
približno jednaka
 Ako
ponovimo razmatranje o središtu masa sustava od konačno mnogo
materijalnih točaka, dobivamo za apscisu središta masa
gdje
Ako
ponovimo razmatranje o središtu masa sustava od konačno mnogo
materijalnih točaka, dobivamo za apscisu središta masa
gdje  predstavlja ukupnu masu tijela
predstavlja ukupnu masu tijela  U ovoj
formuli brojnik je integralna suma za funkciju
U ovoj
formuli brojnik je integralna suma za funkciju
 po području
po području  Ako je gustoća mase integrabilna funkcija,
zaključujemo da je
Na sličan način možemo dobiti
Ako je gustoća mase integrabilna funkcija,
zaključujemo da je
Na sličan način možemo dobiti
Ako se radi o vrlo tankom materijalnom tijelu  (ravna ploča), koje
zauzima u ravnini
(ravna ploča), koje
zauzima u ravnini  zatvoreno područje
zatvoreno područje  i čija gustoća
mase je
i čija gustoća
mase je
 onda su koordinate središta masa
onda su koordinate središta masa
Konačno, ako se radi o tankom ravnom štapu, na segmentu ![$ [a,b],$](img1000.gif) čija je
gustoća mase
čija je
gustoća mase  onda je središte masa
onda je središte masa
Veličine koje se pojavljuju u brojnicima koordinata središta masa,
se zovu statički momenti
Tako se integrali
redom zovu statički momenti tijela  u odnosu na ravninu
u odnosu na ravninu 


Integrali
se zovu redom statički
momenti ravne ploče  u odnosu na
u odnosu na  -os,
-os,  -os.
-os.
Integral
se zove statički moment štapa u odnosu na ishodište.
Primjer 2.18
Naći statički moment valjka radiusa baze

i visine

u odnosu na ravninu baze valjka.
Rješenje. Ako se ne kaže ništa o gustoći mase, onda se
pretpostavlja da je

Neka su dvije mase  i
i  povezane tankom šipkom, čiju masu
možemo zanemariti. Pretpostavimo da okomito na šipku djeluje sila
(na pr. sila teža). Postoji točka
povezane tankom šipkom, čiju masu
možemo zanemariti. Pretpostavimo da okomito na šipku djeluje sila
(na pr. sila teža). Postoji točka  na šipki takva da sistem
ostane u stanju ravnoteže, ako ga u toj točki objesimo. Razlog tome
je taj da je suma momenata sile u odnosu na točku
na šipki takva da sistem
ostane u stanju ravnoteže, ako ga u toj točki objesimo. Razlog tome
je taj da je suma momenata sile u odnosu na točku  jednaka nuli.
Ta točka se zove težište. Pretpostavimo da
se masa
jednaka nuli.
Ta točka se zove težište. Pretpostavimo da
se masa  nalazi u položaju
nalazi u položaju  i da je na tom mjestu
akceleracija sile
i da je na tom mjestu
akceleracija sile  a masa
a masa  u
u  i da je na tom mjestu
akceleracija sile
i da je na tom mjestu
akceleracija sile  Dakle, mora biti
odnosno
Dakle, mora biti
odnosno
Da je bilo više masa,
 sa svojim položajima
sa svojim položajima
 na sličan način dobili bismo
na sličan način dobili bismo
Neka je dano materijalno tijelo T, s gustoćom mase
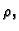 koje zauzima u prostoru neko zatvoreno područje
koje zauzima u prostoru neko zatvoreno područje  Ako ga objesimo u jednoj točki, onda ono u polju sile zauzme
ravnotežni položaj. Uzrok tome je taj što je suma svih momenata
sile, od najmanjih djelića tijela jednaka nuli. Opišemo oko tijela
minimalni kvadar
Ako ga objesimo u jednoj točki, onda ono u polju sile zauzme
ravnotežni položaj. Uzrok tome je taj što je suma svih momenata
sile, od najmanjih djelića tijela jednaka nuli. Opišemo oko tijela
minimalni kvadar  stranica paralelnih koordinatnim ravninama, i
definiramo gustoću mase na
stranica paralelnih koordinatnim ravninama, i
definiramo gustoću mase na 
Kao kod definicije trostrukog integrala podijelimo kvadar  na
mnogo malih kvadara
na
mnogo malih kvadara  U svakom od njih izaberemo jednu točku
U svakom od njih izaberemo jednu točku
 Pretpostavimo da je masa kvadra
Pretpostavimo da je masa kvadra  koncentrirana u toj točki. Tada na sličan način kao gore dobivamo
U brojniku imamo integralnu sumu funkcije
koncentrirana u toj točki. Tada na sličan način kao gore dobivamo
U brojniku imamo integralnu sumu funkcije
 a u nazivniku funkcije
a u nazivniku funkcije
 Tako, uz uvjet da su funkcije
Tako, uz uvjet da su funkcije
 i
i  integrabilne, imamo apscisu težišta
Na sličan način možemo dobiti ostale koordinate težišta
integrabilne, imamo apscisu težišta
Na sličan način možemo dobiti ostale koordinate težišta
U nazivnicima koordinata težišta se pojavljuje integral, koji
predstavlja ukupnu silu koja djeluje na tijelo (u slučaju sile teže
to je težina).
Ako se radi o tankoj ploči, u ravnini  čija je gustoća
mase
čija je gustoća
mase
 onda su koordinate težišta
onda su koordinate težišta
Konačno, ako se radi o tankom ravnom štapu, na segmentu ![$ [a,b],$](img1000.gif) čija je
gustoća mase
čija je
gustoća mase  onda je težište
onda je težište
Ako sila svakoj točki tijela daje jednako ubrzanje, tj. ako je sila
konstanta, onda je njezina akceleracija  konstanta, pa se može izlučiti
ispred integrala, i skratiti. U tom slučaju se težište poklapa sa
središtem masa. To se događa kad se u polju sile teže nalazi
tijelo, čije dimenzije nisu tako velike da bi razlika udaljenosti
pojedinih dijelova tijela do središta Zemlje bila relativno
značajna.
konstanta, pa se može izlučiti
ispred integrala, i skratiti. U tom slučaju se težište poklapa sa
središtem masa. To se događa kad se u polju sile teže nalazi
tijelo, čije dimenzije nisu tako velike da bi razlika udaljenosti
pojedinih dijelova tijela do središta Zemlje bila relativno
značajna.
Neka se materijalna točka mase  jednoliko giba po kružnici u
ravnini
jednoliko giba po kružnici u
ravnini  oko ishodišta. Moment vrtnje (moment količine
gibanja) se definira kao
gdje je
oko ishodišta. Moment vrtnje (moment količine
gibanja) se definira kao
gdje je  radijvektor položaja materijalne točke, a
radijvektor položaja materijalne točke, a
 njezina brzina (linearna). Kod ovakvog gibanja je
njezina brzina (linearna). Kod ovakvog gibanja je
 pa je
Linearna brzina
pa je
Linearna brzina  se može izraziti pomoću kutne brzine
se može izraziti pomoću kutne brzine
 kao
gdje je
kao
gdje je
 Odatle, budući da je
Odatle, budući da je
 pa nakon uvrštavanja imamo
Ako prihvatimo da je kod takvog gibanja prirodno za brzinu uzeti
pa nakon uvrštavanja imamo
Ako prihvatimo da je kod takvog gibanja prirodno za brzinu uzeti
 onda veličina
odgovara onome što je inercijska masa prilikom jednolikog gibanja po
pravcu. Zato se
onda veličina
odgovara onome što je inercijska masa prilikom jednolikog gibanja po
pravcu. Zato se  zove moment inercije materijalne
točke. Primjetimo da je
zove moment inercije materijalne
točke. Primjetimo da je
 zapravo kvadrat udaljenosti od
središta vrtnje.
zapravo kvadrat udaljenosti od
središta vrtnje.
Neka je dano materijalno tijelo  gustoće mase
gustoće mase 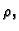 koje u
prostoru zauzima zatvoreno
područje
koje u
prostoru zauzima zatvoreno
područje  i neka se to tijelo jednoliko giba na pr. oko osi
i neka se to tijelo jednoliko giba na pr. oko osi  Kako sada izgleda formula za intenzitet momenta vrtnje?
Da bismo odgovorili na to pitanje, opišemo oko tijela minimalni
kvadar
Kako sada izgleda formula za intenzitet momenta vrtnje?
Da bismo odgovorili na to pitanje, opišemo oko tijela minimalni
kvadar  čije su stranice paralelne koordinatnim ravninama, i
definiramo gustoću mase kvadra
čije su stranice paralelne koordinatnim ravninama, i
definiramo gustoću mase kvadra  kao
kao
Subdivizijom podijelimo  na male kvadre
na male kvadre  Ako u svakom
od njih izaberemo jednu točku
Ako u svakom
od njih izaberemo jednu točku
 onda je
moment inercije približno jednak
što je integralna suma za funkciju
onda je
moment inercije približno jednak
što je integralna suma za funkciju
 po
kvadru
po
kvadru  Dakle, možemo zaključiti da je moment inercije tijela
jednak
Primijetimo da
Dakle, možemo zaključiti da je moment inercije tijela
jednak
Primijetimo da  predstavlja udaljenost točke
predstavlja udaljenost točke  tijela od osi vrtnje.
tijela od osi vrtnje.
Općenito, neka je pravac  os vrtnje, i
os vrtnje, i
 udaljenost točke
udaljenost točke  tijela od pravca
tijela od pravca  Broj
Broj
se zove
moment
inercije tijela  u odnosu na pravac
u odnosu na pravac  .
.
Primjer 2.19
Naći moment inercije stošca radiusa baze

visine

u odnosu na njegovu os simetrije.
Rješenje. Budući da se ništa ne kaže o gustoći mase,
pretpostavljamo da je
 Riješimo taj zadatak prelaskom
u cilindrični koordinatni sustav. Iz sličnosti trokuta
Riješimo taj zadatak prelaskom
u cilindrični koordinatni sustav. Iz sličnosti trokuta
slijedi

Tako je
Ako taj rezultat želimo iskazati pomoću mase, onda, zbog


volumen

pa je
Primjer 2.20
Nađimo kinetičku energiju tijela koje rotira jednoliko
oko neke osi. Radi određenosti pretpostavimo da tijelo
zauzima područje

u prostoru i da rotira oko osi

Rješenje. Malen kvadar tijela oko točke  ima masu
približno
ima masu
približno
Prilikom rotacije oko osi

kutnom brzinom

taj dio tijela ima
kinetičku energiju približno
gdje je

linearna brzina točke. Ukupna kinetička
energija je dakle približno
Odatle slijedi da je točna vrijednost kinetičke energije tijela
Dakle kinetička energija tijela prilikom rotacije oko neke osi jednaka je
polovini umnoška momenta inercije tijela u odnosu na tu os i kvadrata
kutne brzine.
Neka je
![$ I=[a,b]\times [c,d],$](img1107.gif) i neka je
i neka je
 neprekidna
funkcija na
neprekidna
funkcija na  Ako
Ako  integriramo po
integriramo po  onda dobivamo funkciju od
onda dobivamo funkciju od 
Postavlja se pitanje da li funkciju  možemo derivirati i integrirati po
možemo derivirati i integrirati po
 i kako? Što se tiče integriranja odgovor je dan ranije, kad smo
definirali dvostruki integral i dali formule za računanje
Dakle integrirati se može i to tako da se najprije integrira po
i kako? Što se tiče integriranja odgovor je dan ranije, kad smo
definirali dvostruki integral i dali formule za računanje
Dakle integrirati se može i to tako da se najprije integrira po  To neki
puta može biti lakše nego najprije računati
To neki
puta može biti lakše nego najprije računati  pa onda integrirati.
Ako područje nije pravokutnik, onda granice nisu konstante. U tom slučaju
se, prilikom zamjene poretka integracije, moraju odrediti nove granice.
pa onda integrirati.
Ako područje nije pravokutnik, onda granice nisu konstante. U tom slučaju
se, prilikom zamjene poretka integracije, moraju odrediti nove granice.
Za deriviranje funkcije  imamo sljedeće pravilo.
imamo sljedeće pravilo.
Teorem 13
(Leibnizovo pravilo).
Neka je

neprekidna funkcija na
![$ I=[a,b]\times [c,d],$](img1107.gif)
i neka ima neprekidnu
parcijalnu derivaciju po

na

Tada je funkcija
klase
![$ C^1([a,b]),$](img1519.gif)
i vrijedi
Dokaz.

Primjer 2.21
Rješenje.
Odatle
Za

je

pa je tako

Dakle
Ako  nije pravokutnik, tj. ako su granice
nije pravokutnik, tj. ako su granice  i
i  funkcije od
funkcije od
 i to klase
i to klase
![$ C^1([a,b]),$](img1519.gif) onda imamo
onda imamo
 |
(2.7) |
U tom slučaju formula za  glasi
glasi
 |
(2.8) |
Zaista, neka je  funkcija od tri varijable
funkcija od tri varijable 
Ako su  i
i  funkcije od
funkcije od  onda imamo složenu funkciju od jedne
varijable
ona ima derivaciju i ta glasi
U ovoj formuli je
onda imamo složenu funkciju od jedne
varijable
ona ima derivaciju i ta glasi
U ovoj formuli je
 je
derivacija integrala (2.7) po donjoj granici, a
je
derivacija integrala (2.7) po donjoj granici, a
 je derivacija istog inegrala po gornjoj granici.
Derivacija integrala po gornjoj granici jednaka je vrijednosti
podintegralne funkcije u toj granici (v. 8.5)
Donju granicu možemo učiniti gornjom promjenom predznaka, dakle
Nakon uvrštenja dobivamo upravo traženu formulu.
je derivacija istog inegrala po gornjoj granici.
Derivacija integrala po gornjoj granici jednaka je vrijednosti
podintegralne funkcije u toj granici (v. 8.5)
Donju granicu možemo učiniti gornjom promjenom predznaka, dakle
Nakon uvrštenja dobivamo upravo traženu formulu.
Primjer 2.22
Neka je
Treba naći

Rješenje. Gornji integral je neelementaran, pa se  ne
može odrediti pomoću konačno mnogo elementarnih funkcija. Ipak,
zahvaljujući formuli (2.8), derivaciju možemo naći.
ne
može odrediti pomoću konačno mnogo elementarnih funkcija. Ipak,
zahvaljujući formuli (2.8), derivaciju možemo naći.
- 1.
- Što je središte masa, i kako se računa?
- 2.
- Što je težište, i kako se računa? Uz koji uvjet se težište
i središte masa podudaraju?
- 3.
- Što je statički moment, i kako se računa?
- 4.
- Što je moment inercije, i kako se računa?
- 5.
- Iskažite Leibnizovo pravilo za deriviranje pod znakom
integrala.
- 6.
- Napišite formulu za deriviranje pod znakom integrala, ako
granice integracije ovise o varijabli po kojoj se derivira i
objasnite je.
- 1.
- Naći središte mase polukugle radiusa

Rješenje. Očito je

Volumen polukugle je
 pa je tako
pa je tako
- 2.
- Naći središte mase homogenog kružnog isječka radiusa
 i kuta
i kuta

Slika 2.14:
Kružni isječak.
|
|
Rješenje.
Dakle
- 3.
- Naći statičke momente lika koji određuju jedan svod
cikloide i os

Slika 2.15:
Lik omeđen cikloidom.
|
|
Rješenje. Pretpostavljamo da je  Cikloida je
zadana s
Cikloida je
zadana s
Tako je
- 4.
- Naći statički moment štapa duljine
 u odnosu na jedan
kraj, ako se gustoća mase mijenja linearno od iznosa
u odnosu na jedan
kraj, ako se gustoća mase mijenja linearno od iznosa  na tom kraju
do
na tom kraju
do
 na drugom kraju.
na drugom kraju.
Rješenje.
pa slijedi
- 5.
- Dokažite sljedeći teorem (Steinerov
teorem) Moment
inercije
 tijela
tijela  u odnosu na proizvoljnu os
u odnosu na proizvoljnu os  jednak je
zbroju momenta inercije
jednak je
zbroju momenta inercije  tijela
tijela  u odnosu na os koja je
paralelna s
u odnosu na os koja je
paralelna s  i prolazi središtem masa tijela
i prolazi središtem masa tijela  i umnoška
mase
i umnoška
mase  tijela i kvadrata udaljenosti
tijela i kvadrata udaljenosti  osi
osi  i
i  tj. formulom
tj. formulom
Rješenje. Pretpostavimo da tijelo  zauzima u prostoru zatvoreno područje
zauzima u prostoru zatvoreno područje
 Neka je njegova gustoća mase
Neka je njegova gustoća mase  Također, radi
jednostavnosti dokaza, pretpostavimo da su osi
Također, radi
jednostavnosti dokaza, pretpostavimo da su osi  i
i  paralelne s
osi
paralelne s
osi  tj. okomite na ravninu
tj. okomite na ravninu  Neka je
Neka je  proizvoljna
točka tijela
proizvoljna
točka tijela  Povucimo točkom
Povucimo točkom  ravninu okomitu na osi
ravninu okomitu na osi  i
i
 Neka su točke
Neka su točke
 i
i
 sjecišta te ravnine i pravaca
sjecišta te ravnine i pravaca  i
i
 Budući da je ravnina paralelna s ravninom
Budući da je ravnina paralelna s ravninom  slijedi
slijedi
 i također
i također
 Prema tome,
kvadrat udaljenosti točaka
Prema tome,
kvadrat udaljenosti točaka  i
i  je
je
U prvoj uglatoj zagradi je kvadrat udaljenosti točke  od osi kroz centar
masa, u drugoj uglatoj zagradi je kvadrat udaljenosti osi, i osim toga
uočimo da
od osi kroz centar
masa, u drugoj uglatoj zagradi je kvadrat udaljenosti osi, i osim toga
uočimo da
 i
i
 ne ovise o
ne ovise o  Tako
imamo
Integral
Tako
imamo
Integral
 jednak je masi
jednak je masi  tijela
tijela
 Zatim, iz formule za
Zatim, iz formule za  slijedi
Na isti način
Dakle, doista vrijedi formula
slijedi
Na isti način
Dakle, doista vrijedi formula
- 6.
-

Rješenje.
Supstitucijom


 slijedi
Odatle
Dakle
slijedi
Odatle
Dakle
 ne ovisi o
ne ovisi o  pa prema tome
Dakle
pa prema tome
Dakle





Next: Krivulje i krivuljni integrali
Up: Višestruki integrali
Previous: Računanje integrala supstitucijom
Contents
Index
Salih Suljagic
2000-03-11
![]() materijalnih točaka s masama
materijalnih točaka s masama
![]() u
prostoru tako da su njihovi radijvektori
u
prostoru tako da su njihovi radijvektori
![]() Točka
Točka ![]() čiji je
radijvektor
čiji je
radijvektor ![]() sa svojstvom da je
sa svojstvom da je



![]() koje zauzima u prostoru neko zatvoreno područje
koje zauzima u prostoru neko zatvoreno područje
![]() Želimo naći središte masa tijela
Želimo naći središte masa tijela ![]() U tu svrhu opišemo
oko tijela minimalni kvadar
U tu svrhu opišemo
oko tijela minimalni kvadar ![]() stranica paralelnih koordinatnim ravninama,
i definiramo gustoću mase na kvadru
stranica paralelnih koordinatnim ravninama,
i definiramo gustoću mase na kvadru ![]()






![]() (ravna ploča), koje
zauzima u ravnini
(ravna ploča), koje
zauzima u ravnini ![]() zatvoreno područje
zatvoreno područje ![]() i čija gustoća
mase je
i čija gustoća
mase je
![]() onda su koordinate središta masa
onda su koordinate središta masa

![]() čija je
gustoća mase
čija je
gustoća mase ![]() onda je središte masa
onda je središte masa





![]()



![]() sa svojim položajima
sa svojim položajima
![]() na sličan način dobili bismo
na sličan način dobili bismo

![]() koje zauzima u prostoru neko zatvoreno područje
koje zauzima u prostoru neko zatvoreno područje ![]() Ako ga objesimo u jednoj točki, onda ono u polju sile zauzme
ravnotežni položaj. Uzrok tome je taj što je suma svih momenata
sile, od najmanjih djelića tijela jednaka nuli. Opišemo oko tijela
minimalni kvadar
Ako ga objesimo u jednoj točki, onda ono u polju sile zauzme
ravnotežni položaj. Uzrok tome je taj što je suma svih momenata
sile, od najmanjih djelića tijela jednaka nuli. Opišemo oko tijela
minimalni kvadar ![]() stranica paralelnih koordinatnim ravninama, i
definiramo gustoću mase na
stranica paralelnih koordinatnim ravninama, i
definiramo gustoću mase na ![]()




![]() čija je gustoća
mase
čija je gustoća
mase
![]() onda su koordinate težišta
onda su koordinate težišta

![]() čija je
gustoća mase
čija je
gustoća mase ![]() onda je težište
onda je težište

![]() konstanta, pa se može izlučiti
ispred integrala, i skratiti. U tom slučaju se težište poklapa sa
središtem masa. To se događa kad se u polju sile teže nalazi
tijelo, čije dimenzije nisu tako velike da bi razlika udaljenosti
pojedinih dijelova tijela do središta Zemlje bila relativno
značajna.
konstanta, pa se može izlučiti
ispred integrala, i skratiti. U tom slučaju se težište poklapa sa
središtem masa. To se događa kad se u polju sile teže nalazi
tijelo, čije dimenzije nisu tako velike da bi razlika udaljenosti
pojedinih dijelova tijela do središta Zemlje bila relativno
značajna.

![]() gustoće mase
gustoće mase ![]() koje u
prostoru zauzima zatvoreno
područje
koje u
prostoru zauzima zatvoreno
područje ![]() i neka se to tijelo jednoliko giba na pr. oko osi
i neka se to tijelo jednoliko giba na pr. oko osi ![]() Kako sada izgleda formula za intenzitet momenta vrtnje?
Da bismo odgovorili na to pitanje, opišemo oko tijela minimalni
kvadar
Kako sada izgleda formula za intenzitet momenta vrtnje?
Da bismo odgovorili na to pitanje, opišemo oko tijela minimalni
kvadar ![]() čije su stranice paralelne koordinatnim ravninama, i
definiramo gustoću mase kvadra
čije su stranice paralelne koordinatnim ravninama, i
definiramo gustoću mase kvadra ![]() kao
kao



![]() os vrtnje, i
os vrtnje, i
![]() udaljenost točke
udaljenost točke ![]() tijela od pravca
tijela od pravca ![]() Broj
Broj

![]() Riješimo taj zadatak prelaskom
u cilindrični koordinatni sustav. Iz sličnosti trokuta
Riješimo taj zadatak prelaskom
u cilindrični koordinatni sustav. Iz sličnosti trokuta




![]() ima masu
približno
ima masu
približno




![]() i neka je
i neka je
![]() neprekidna
funkcija na
neprekidna
funkcija na ![]() Ako
Ako ![]() integriramo po
integriramo po ![]() onda dobivamo funkciju od
onda dobivamo funkciju od ![]()


![]() imamo sljedeće pravilo.
imamo sljedeće pravilo.


![]()




![]() nije pravokutnik, tj. ako su granice
nije pravokutnik, tj. ako su granice ![]() i
i ![]() funkcije od
funkcije od
![]() i to klase
i to klase
![]() onda imamo
onda imamo
![]() funkcija od tri varijable
funkcija od tri varijable ![]()







![]() ne
može odrediti pomoću konačno mnogo elementarnih funkcija. Ipak,
zahvaljujući formuli (2.8), derivaciju možemo naći.
ne
može odrediti pomoću konačno mnogo elementarnih funkcija. Ipak,
zahvaljujući formuli (2.8), derivaciju možemo naći.



![]()






![]() Cikloida je
zadana s
Cikloida je
zadana s



![$\displaystyle M_0=\int_0^{\ell} x\left[\frac{\rho_{\ell}-\rho_0}{\ell}x+\rho_0\right]\,dx=
\frac{2\rho_{\ell}+\rho_0}{6}\ell^2.$](img1568.gif)
![]() zauzima u prostoru zatvoreno područje
zauzima u prostoru zatvoreno područje
![]() Neka je njegova gustoća mase
Neka je njegova gustoća mase ![]() Također, radi
jednostavnosti dokaza, pretpostavimo da su osi
Također, radi
jednostavnosti dokaza, pretpostavimo da su osi ![]() i
i ![]() paralelne s
osi
paralelne s
osi ![]() tj. okomite na ravninu
tj. okomite na ravninu ![]() Neka je
Neka je ![]() proizvoljna
točka tijela
proizvoljna
točka tijela ![]() Povucimo točkom
Povucimo točkom ![]() ravninu okomitu na osi
ravninu okomitu na osi ![]() i
i
![]() Neka su točke
Neka su točke
![]() i
i
![]() sjecišta te ravnine i pravaca
sjecišta te ravnine i pravaca ![]() i
i
![]() Budući da je ravnina paralelna s ravninom
Budući da je ravnina paralelna s ravninom ![]() slijedi
slijedi
![]() i također
i također
![]() Prema tome,
kvadrat udaljenosti točaka
Prema tome,
kvadrat udaljenosti točaka ![]() i
i ![]() je
je
![$\displaystyle I_p = \iiint_{\Omega}\,[{{\left( x - {x_p} \right) }^2} + {{\left( y - {y_p}
\right) }^2}] \,\rho(x,y,z)\,dx\,dy\,dz$](img1586.gif)
![$\displaystyle = \iiint_{\Omega}\,[(x-x_S)^2 +
(y-y_S)^2] \,\rho(x,y,z)\,dx\,dy\,dz$](img1587.gif)
![$\displaystyle + \iiint_{\Omega}\,[(x_S-x_p)^2 +
(y_S-y_p)^2] \,\rho(x,y,z)\,dx\...
..._{\Omega}\,
[(x-x_S)\,(x_S-x_p) + (y-y_S)\,(y_S-y_p)]
\,\rho(x,y,z)\,dx\,dy\,dz$](img1588.gif)











![$\displaystyle C=\lim_{a\rightarrow \infty}\left[
\int_0^{\pi/2} \ln\left(1-\frac{\sin^2\theta}{a^2}\right)\,d\theta+
\pi\ln\frac{a}{a+\sqrt{a^2-1}}\right]=$](img1607.gif)

