Dinamički proračun

I za dinamički je proračun opis konstrukcije većim dijelom jednak opisu za statički proračun. No:

• opterećenja se ne zadaju;
• konstrukcija ne može imati unutarnje zglobove (ležajevi smiju biti nepomični, zglobni ili zglobni klizni).

Za dinamički proračun treba odabrati Frequency analysis u izborniku Analysis. Proračun se može provesti s konzistentnom ili s dijagonalnom matricom masa: u podizborniku Frequency analysis može se odabrati Consistent mass matrix ili Diagonal mass matrix.

Program ispisuje približne vrijednosti perioda T_i (T_i) i frekvencija f_i i $\omega_{i}^{}$ (f_i i omega_i) svojstvenih oblika osciliranja konstrukcije.

Kružne frekvencije $\omega_{i}^{}$ korijeni su rješenja poopćenoga problema svojstvenih vrijednosti

(K - $$\omega^{2}_{}$$M) v = 0,

gdje su K i M matrice krutosti i masa konstrukcije ( M može biti konzistentna ili dijagonalna matrica). Frekvencije f_i definirane su izrazom

f_i = $${\frac{{\omega_i}}{{2 \pi}}}$$,

a periodi su

T_i = 1/f_i.

Normalizirani osnovni oblici osciliranja (točnije: njihove aproksimacije polinomima trećeg stupnja) mogu se prikazati izborom Natural modes u podizborniku Diagrams izbornika Analysis. Mogu se ispisati vrijednosti pomaka odabranoga osnovnog oblika u čvorovima (izborom Values) ili se taj oblik može prikazati kao crtež (izborom Graph) ili animacija (Animate).

Primjer: okvir

Okvirna konstrukcija zadana je sljedećim podacima:

• čvorovi:

  Label	x	y
  1	0,0 [m]	0,0 [m]
  2	1,732 [m]	3,0 [m]
  3	4,732 [m]	3,0 [m]
  4	4,732 [m]	0,0 [m]

• elementi:

  Label	1st node	2nd node
  1	1	2
  2	2	3
  3	3	4

• ležajevi: čvorovi 1 i 4 upeti;

• materijalne karakteristike:

  E = 2, 0 ^. 10⁸  [kN/m²]

  $\varrho$ = 7, 8  [t/m³]

• geometrijske karakteristike:
  • elementi 1 i 2:

    A = 32, 0 ^. 10^-4  [m²]

    I_x = 2, 356 ^. 10^-5  [m⁴]

  • element 3:

    A = 66, 0 ^. 10^-4  [m²]

    I_x = 5, 245 ^. 10^-5  [m⁴]

Proračun s konzistentnom matricom masa daje:

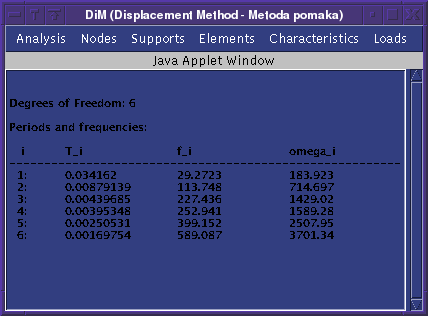
a proračun s dijagonalnom matricom daje:

Prvi, drugi i treći svojstveni oblici osciliranja prikazani su na sljedećim slikama:

Primjer: okvirni element

Za dinamički proračun `konstrukcija' ne mora imati najmanji neophodni broj vanjskih veza za geometrijsku nepromjenjivost.¹

Najjednostavniji je primjer vjerojatno okvirni element bez ležajeva.

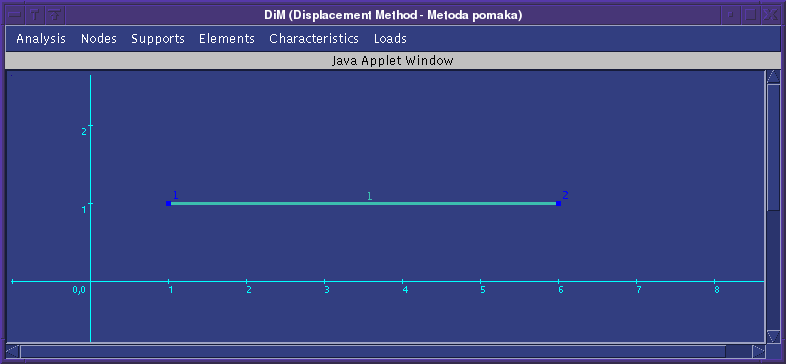
Prva su tri rješenja poopćenoga problema svojstvenih vrijednosti jednaka nuli, što znači da tri stupnja slobode odgovaraju gibanjima krutog tijela u ravnini; na slici je prikazan drugi svojstveni oblik (proračun je proveden s konzistentnom matricom masa).

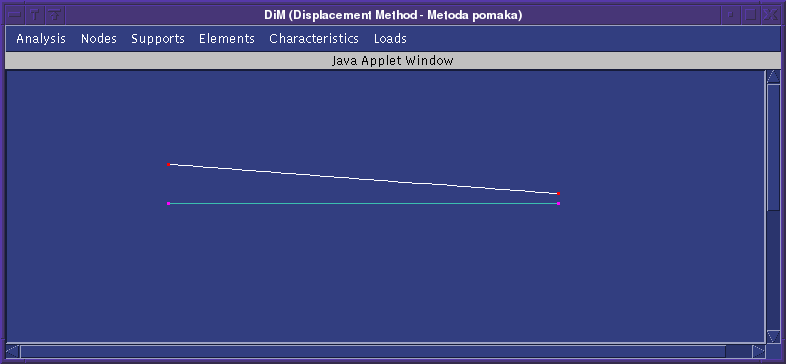
Četvrti, peti i šesti svojstveni oblik uključuju i promjenu oblika elementa; na slici je prikazan peti svojstveni oblik.

Domaća zadaća

Sklop elemenata² zadan je na sljedeći način:

• čvorovi:

  Label	x	y
  1	0,0 [m]	0,0 [m]
  2	2,0 [m]	0,0 [m]
  3	1,0 [m]	3,0 [m]
  4	-1,0 [m]	5,0 [m]
  5	1,0 [m]	6,0 [m]
  6	2,0 [m]	4,0 [m]
  7	1,0 [m]	7,0 [m]

• elementi:

  Label	1st node	2nd node
  1	1	3
  2	3	5
  3	4	5
  4	5	7
  5	5	6
  6	3	2

• materijalne i geometrijske karakteristike svih elemenata:

  E = 3, 0 ^. 10⁷  [kN/m²] (ponuđena vrijednost)

  $\varrho$ = 2, 5  [t/m³] (ponuđena vrijednost)

  b/h = 0, 5/0, 5  [m]

Animirajte osmi svojstveni oblik osciliranja.

... nepromjenjivost.¹

Riječ `konstrukcija' stavili smo u navodnike jer element ili sklop elemenata postoje konstrukcijom tek onda kada može sva opterećenja prenijeti na podlogu - drugim riječima, kada je geometrijski nepromjenjiv.

... elemenata²

Nema ležajeva, pa nećemo upotrijebiti pojam konstrukcije.