U ovom ćemo odjeljku riješiti nekoliko zadataka koje smo već riješili u odjeljku 2.2.12 Mongeovom metodom.
Sjetimo se da smo u Mongeovoj metodi koristili lijevi, a da Rhino koristi desni koordinatni sustav. Ukoliko želimo dobiti rješenje identično onom koje smo dobili korištenjem Mongeove metode, potrebno je svim zadanim točkama, prilikom unosa koordinata, promjeniti predznak \(\small y\)-koordinate. Postupci rješavanja zadataka neće biti jednaki onima u Mongeovoj metodi jer su mogućnosti koje pruža Rhino različite od mogućnosti konstruktivne metode na papiru.
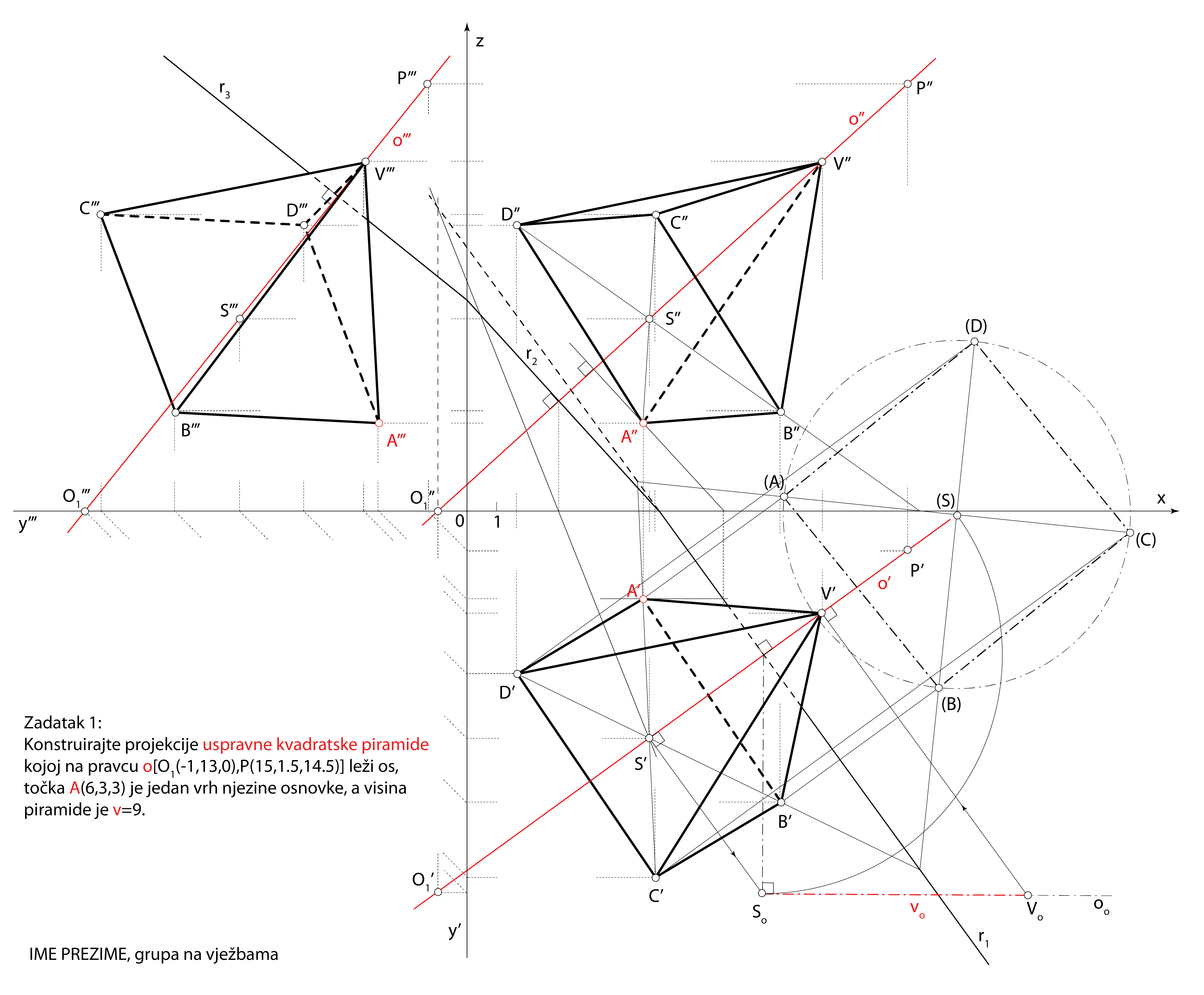
Zadatak 1: Konstruirajte projekcije uspravne kvadratske piramide kojoj na pravcu \(\small o[ O_1(-1,13,0), P(15,1.5,14.5)]\) leži os, točka \(\small A(6,3,3)\) je jedan vrh njezine osnovke, a visina piramide je \(\small v=9\).
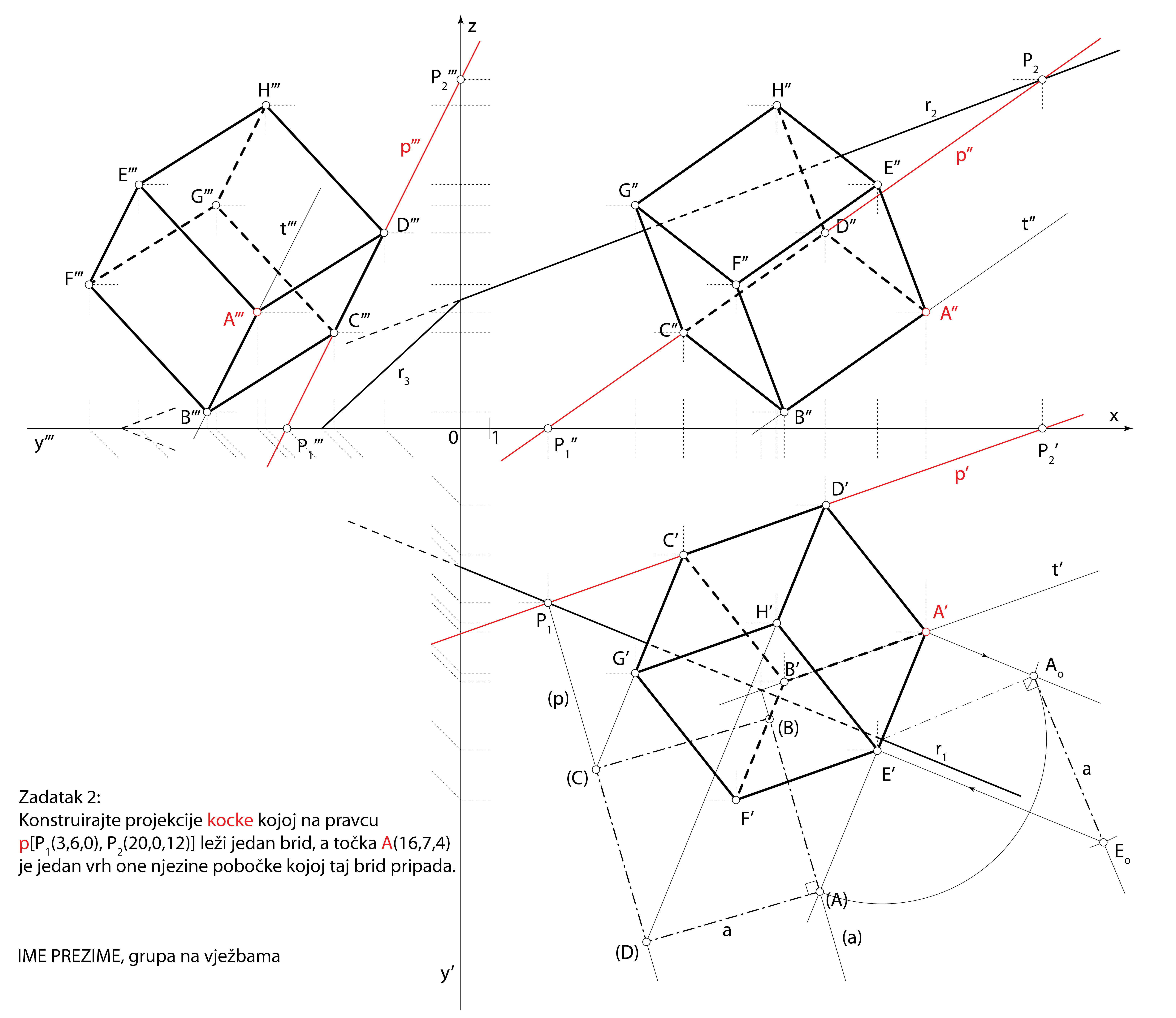
Zadatak 2: Konstruirajte projekcije kocke kojoj na pravcu \(\small p[ P_1(3,6,0), P_2(20,0,12)]\) leži jedan brid, a točka \(\small A(16,7,4)\) je jedan vrh one njezine pobočke kojoj taj brid pripada.
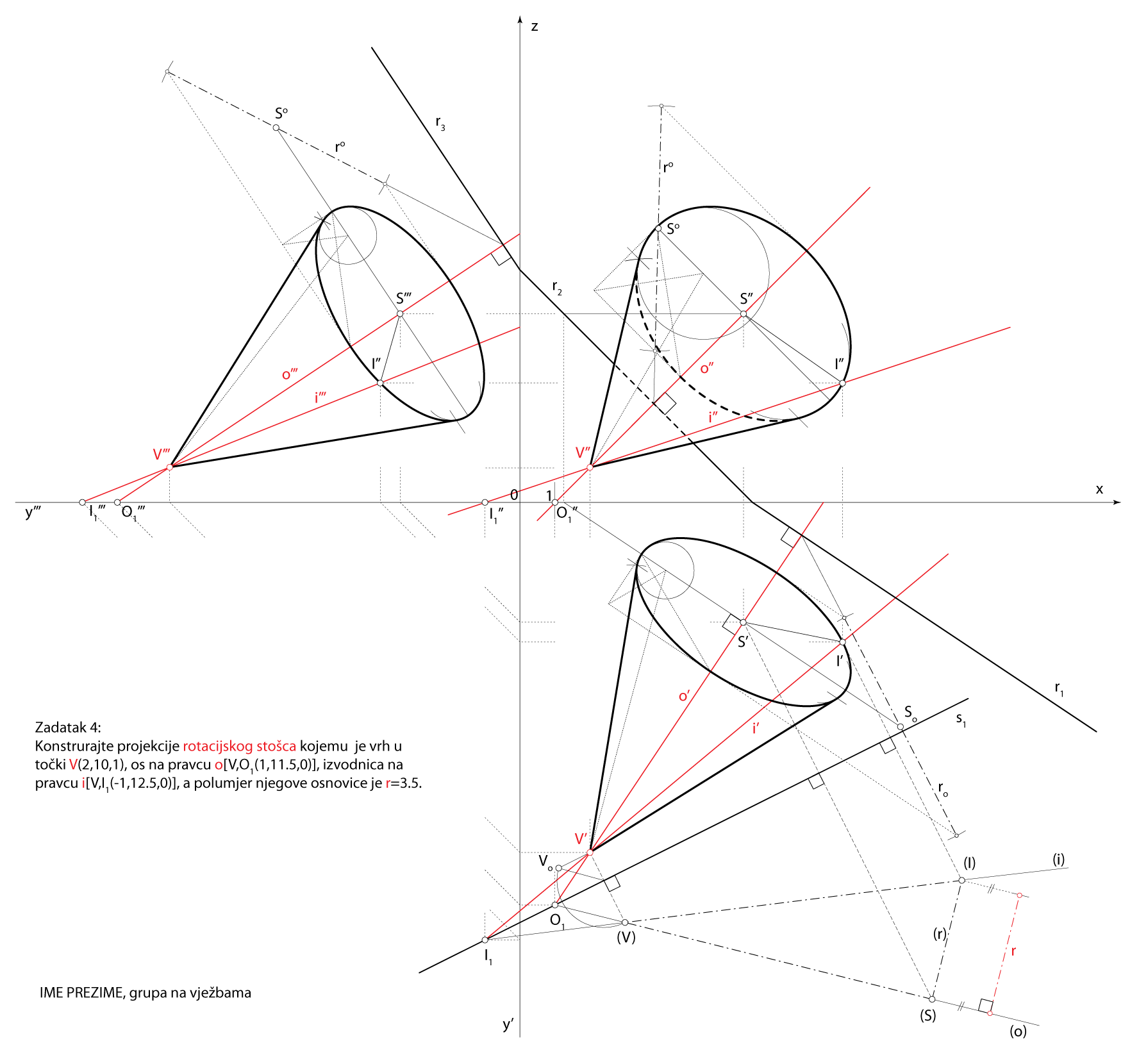
Zadatak 3: Konstruirajte projekcije rotacijskog stošca kojemu je vrh u točki \(\small V(2,10,1)\), os na pravcu \(\small o [V, O_1(1,11.5,0)]\), izvodnica na pravcu \(\small i [ V, I_1(-1,12.5,0)]\), a polumjer njegove osnovke je \(\small r=3.5\).
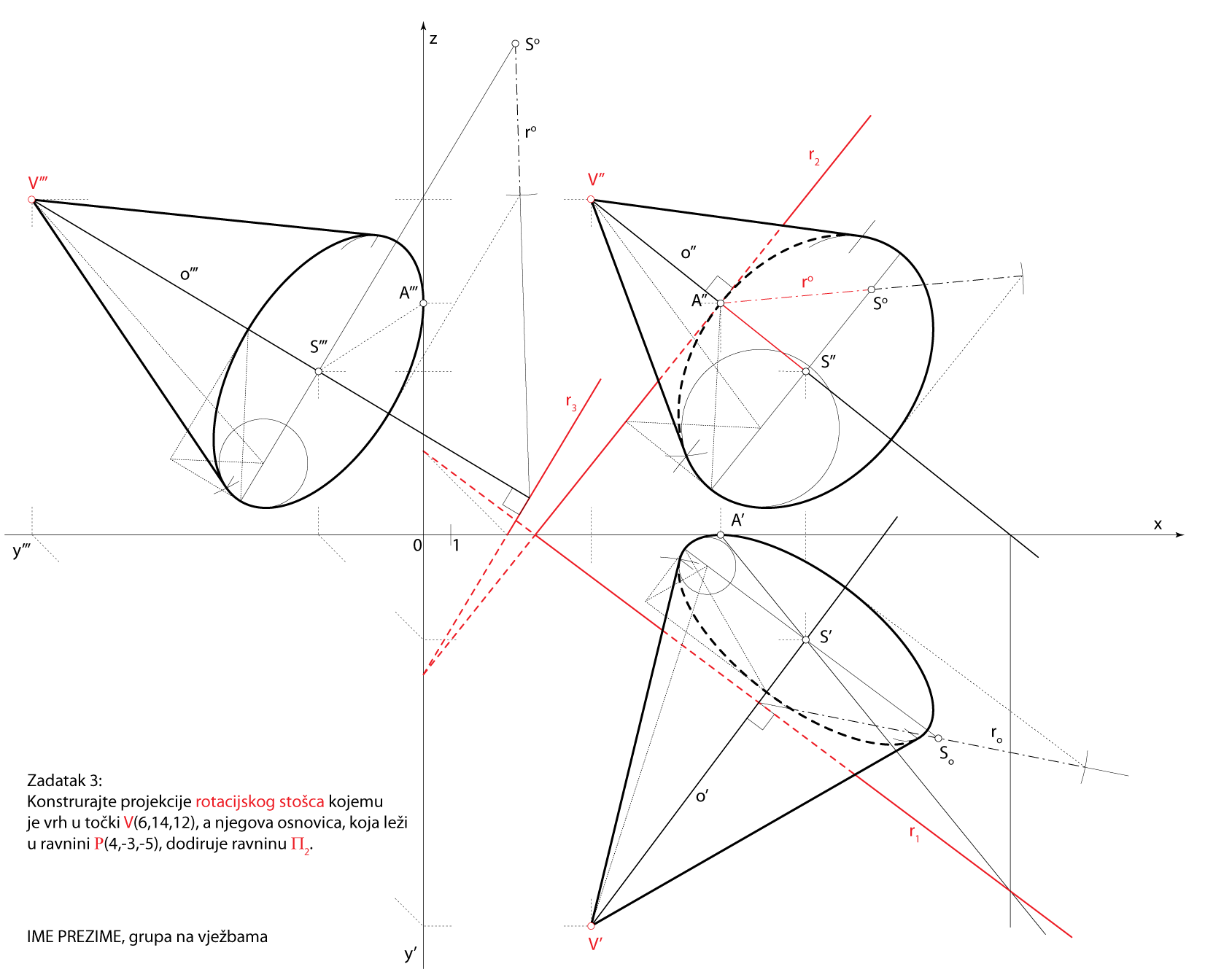
Zadatak 4: Konstruirajte projekcije rotacijskog stošca kojemu je vrh u točki \(\small V(6,14,12)\), a njegova osnovka, koja leži u ravnini P\(\small (4,-3,-5)\), dodiruje ravninu \(\small \Pi_2\).
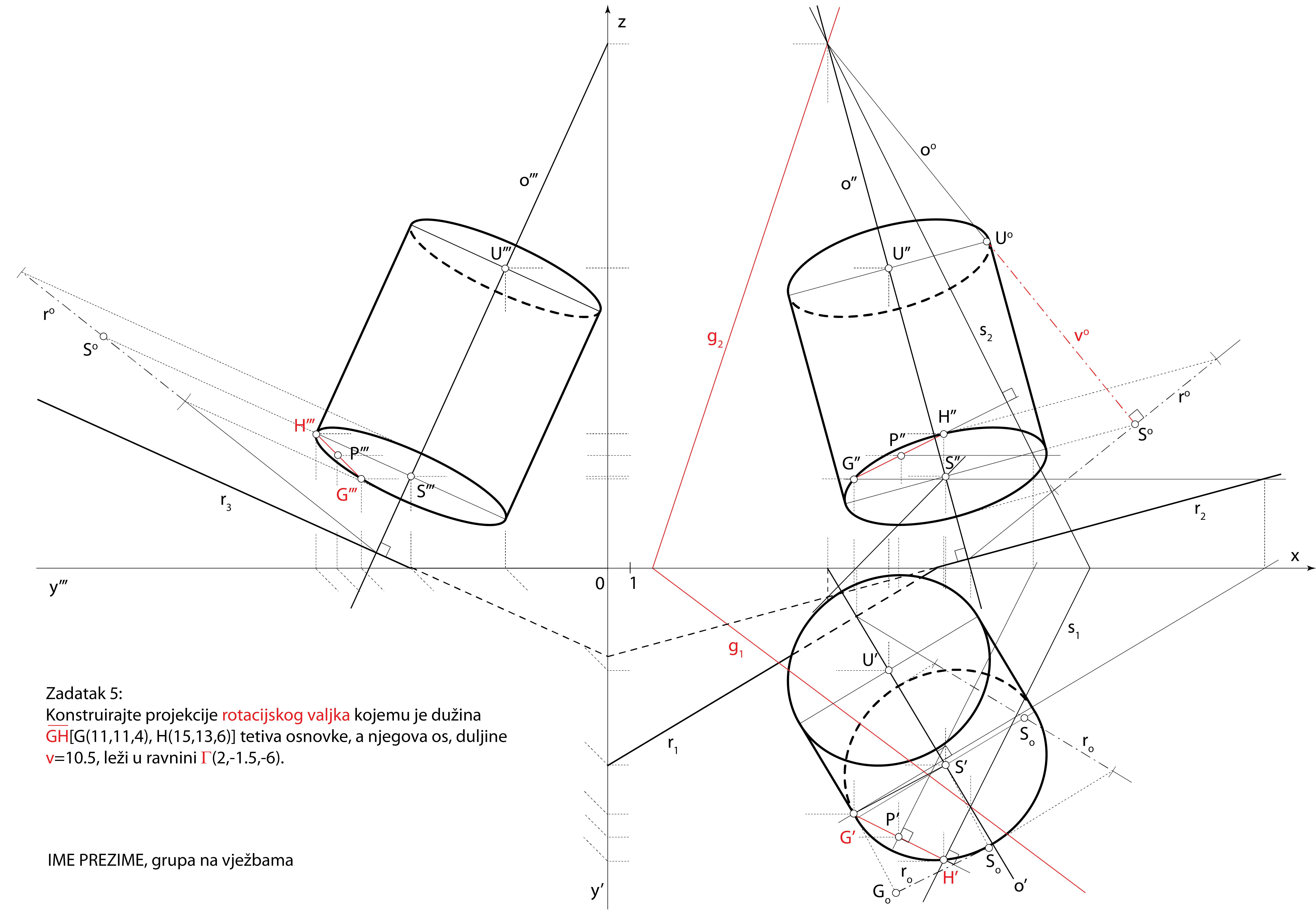
Zadatak 5: Konstruirajte projekcije rotacijskog valjka kojemu je dužina \(\small \overline{GH}[G(11,11,4), H(15,13,6)]\) tetiva osnovke, a njegova os, duljine \(\small v=10.5\), leži u ravnini \(\small\Gamma(2,-1.5,-6)\).