3.3.3. Prodor dvaju stožaca

Osnovni princip konstrukcije točaka prodorne krivulje dvaju stožaca

U slučaju konstrukcije točaka prodorne krivulje dvaju stožaca odabiremo sustav ravnina koji oba stošca siječe po pravcima, odnosno po njihovim izvodnicama. Budući da svaka ravnina koja prolazi vrhom stošca siječe taj stožac po izvodnicama, sustav onih ravnina koje dva stošca sijeku po pravcima prolazi vrhovima tih stožaca. Takve ravnine, dakle, čine pramen ravnina koje prolaze spojnicom vrhova stožaca u prodoru.
Svaka ravnina tog pramena siječe svaki od stožaca u prodoru u dvije izvodnice. Te četiri izvodnice sijeku se u šest točaka, od koji su dvije vrhovi stožaca, a četiri preostala sjecišta su točke prodorne krivulje.

Konstruirati prodornu krivulju znači odrediti skup realnih točaka te krivulje. Izvodnice po kojima ravnine sustava sijeku stošce, mogu biti realne i različite, mogu se podudarati (ako je ravnina sustava tangencijalna ravnina stošca), a mogu biti i imaginarne.

Ako je ravnina sustava takva da se u njoj za svaki od stožaca podudaraju dvije presječne izvodnice, znači da je tangencijalna za obje plohe i da je sjecište dviju presječnih izvodnica dvostruka točka prodorne krivulje zadanih stožaca.

Vidi animaciju 63.
Animacija 63: Pramen ravnina kroz vrhove stožaca u prodoru


Primjeri prodornih krivulja dvaju stožaca

Prave krivulje 4. reda

  • Ako niti jedan stožac ne prodire u potpunosti kroz onaj drugi, odnosno na svakom od stožaca u prodoru postoje izvodnice koje nemaju realnih probodišta s drugim stošcem, prodorna je krivulja jednodijelna. Takav prodor nazivamo nepotpunim prodorom ili zadorom (vidi sliku 377).
  • Ako jedan od stožaca potpuno prodire kroz drugi, ako dakle svaka od njegovih izvodnica probada drugi stožac u dvije realne točke, prodorna je krivulja dvodijelna. Takav prodor nazivamo potpunim prodorom (vidi sliku 378).
Prodorna krivulja dvaju stožaca imat će dvostruku točku u dva slučaja:
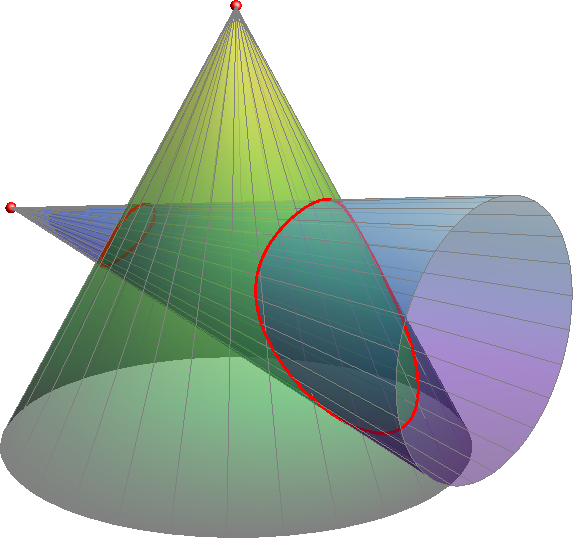
  • Ako oba stošca imaju u jednoj točki (koja je regularna točka za svaki) zajedničku tangencijalnu ravninu, ta je točka dvostruka točka njihove prodorne krivulje (vidi sliku 379).
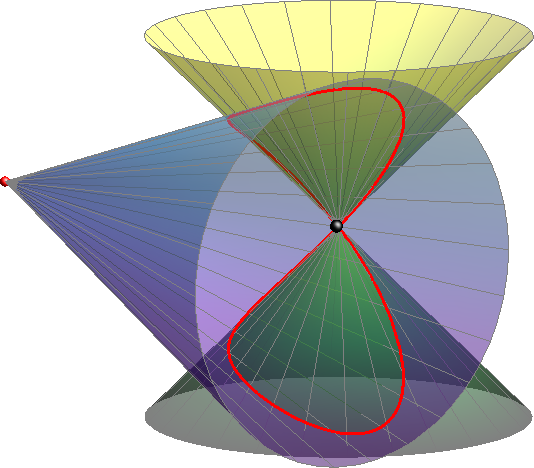
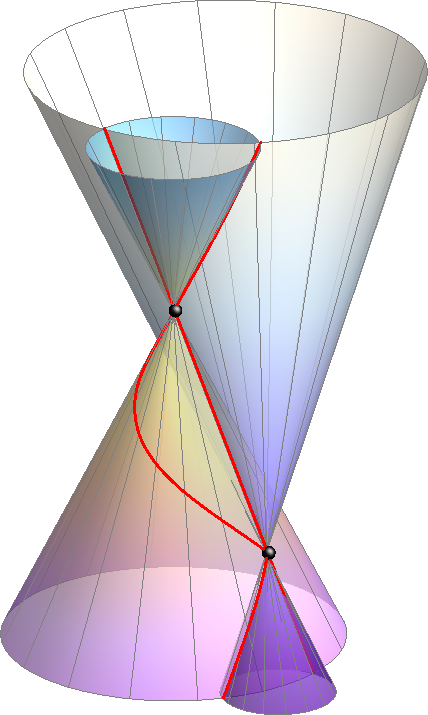
  • Ako jedan od stožaca prolazi vrhom drugoga. Kako je vrh dvostruka točka stošca, bit će ujedno i dvostruka točka prodorne krivulje (vidi sliku 380).
Slika 377: Zador
Slika 378: Potpuni prodor Slika 379: Dvostruka točka Slika 380: Dvostruka točka


Raspadnute krivulje 4. reda

Do potpunog raspada prodorne krivulje dvaju stožaca dolazi u slučaju kada stošci imaju isti vrh. Tada naime stošci imaju zajedničke četiri izvodnice koje su spojnice njihovih vrhova sa četiri sjecišta njihovih osnovica (u bilo kojoj ravnini koja ne prolazi vrhom). Kako ta sjecišta mogu biti realna i različita, realna i poklopljena ili u parovima konjugirano imaginarna, takve mogu biti i presječne izvodnice.
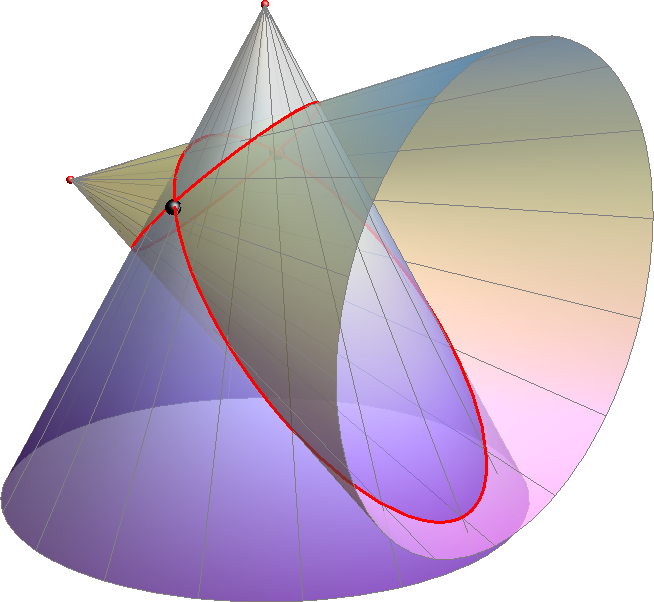
  • Dakle, svaka se dva stošca sa zajedničkim vrhom prodiru u četiri pravca koji prolaze njihovim vrhom (vidi sliku 381).
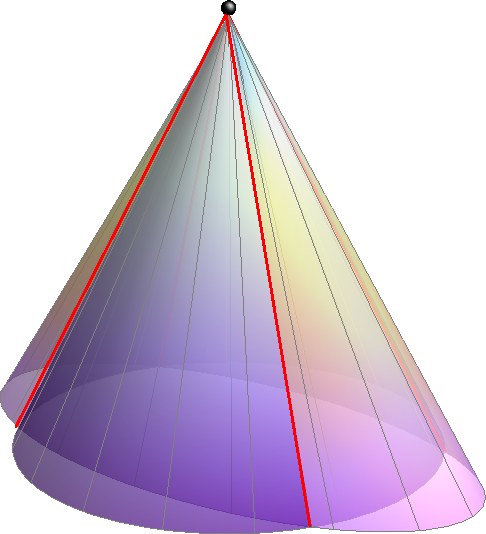
Pri prodoru dvaju stožaca ne može doći do raspada prodorne krivulje 4. reda na dva različita pravca i koniku. Naime, u tom bi slučaju sjecište tih pravaca bio zajednički vrh tih stožaca, a tada se prodorna krivulja raspada na četiri pravca. Međutim, ako dva stošca imaju zajedničku jednu izvodnicu i tangencijalnu ravninu duž te izvodnice, tada je ona dvostruko brojeni pravac u raspadu njihova prodora, a preostali je dio neka konika.
  • Ako dakle dva stošca nemaju isti vrh, ali imaju zajedničku izvodnicu i duž nje tangecijalnu ravninu, njihova će se prodorna krivulja raspasti na dvostruki pravac i koniku (vidi sliku 382).
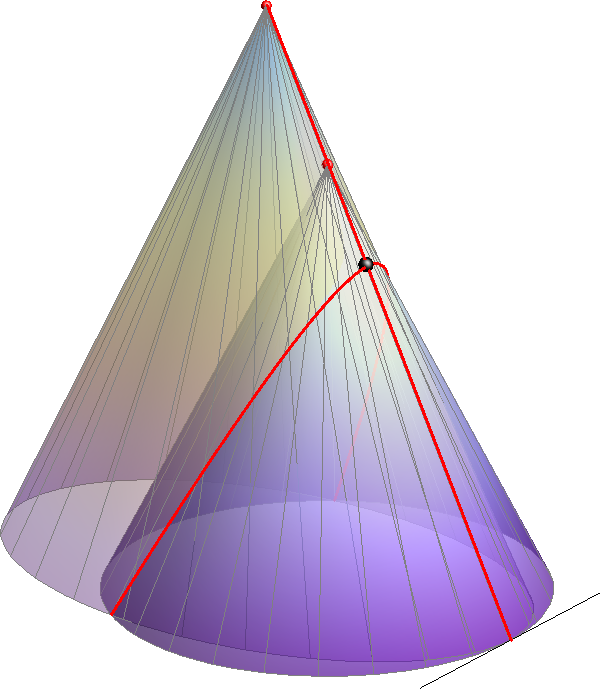
  • Ako dva stošca imaju zajedničku izvodnicu, a nemaju isti vrh ni tangencijalnu ravninu duž zajedničke izvodnice, tada se njihova prodorna krivulja raspada na pravac i krivulju 3. reda (vidi sliku 383).
  • Ako stošci imaju dvije zajedničke tangencijalne ravnine, a nemaju zajedničku ni jednu izvodnicu, njihova prodorna krivulja ima dvije dvostruke točke i raspada se na dvije konike (vidi sliku 384). Nužan uvjet za ovakav raspad prodorne krivulje rotacijskih stožaca je taj da im se osi sijeku.
Slika 381: Četiri pravca Slika 382: Dvostruki pravac i konika Slika 383: Pravac i krivulja 3. reda Slika 384: Dvije konike



Sonja Gorjanc - GeomTeh3D - Razvojni projekt Sveučiliša u Zagrebu