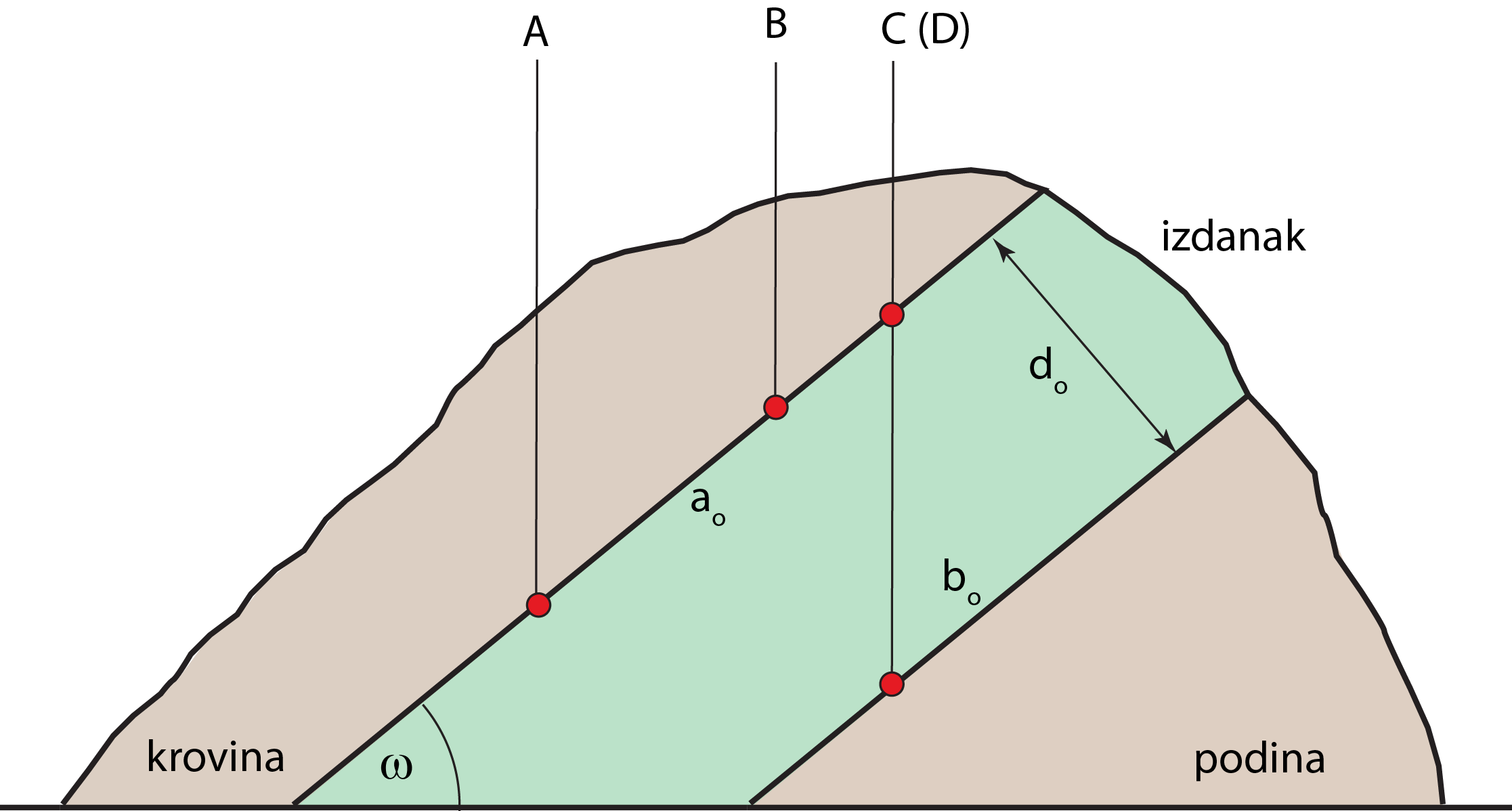
Udaljenost između krovinske i podinske ravnine nazivamo debljinom sloja \(\small d\).
Presjek sloja s površinom terena zove se izdanak.

Slika 252
|
Sloj
je osnovna jedinica sedimentnih ili taložnih stijena. Omeđen je dvjema
plohama, gornjom i donjom slojnom plohom. Radi lakšega geometrijskog prikaza te ćemo plohe aproksimirati paralelnim ravninama te označavati s \(\small \alpha\) i \(\small \beta\). |
|
Dio terena (stijenske mase) iznad gornje ravnine sloja zove se krovina, a onaj ispod donje ravnine sloja podina.
Zbog toga ćemo ravnine \(\small \alpha\) i \(\small \beta\) nazivati krovinskom
i podinskom ravninom. Udaljenost između krovinske i podinske ravnine nazivamo debljinom sloja \(\small d\). Presjek sloja s površinom terena zove se izdanak. |
 Slika 252 |
| Kako se sloj nalazi pod površinom Zemlje, dakle unutar jedne topografske plohe ili terena, najpogodnija metoda za njegovo rješavanje je kotirana projekcija. |
Položaj sloja u prirodi određuje se:
Kut \(\small \gamma\) zovemo kutom pada sloja, a kut \(\small \gamma +90^\circ\) kutom pružanja sloja. |
 Slika 253 |
|
Pri konstruktivnom rješavanju sloja razlikovat ćemo dva tipa zadataka. 1. tip zadataka |
|
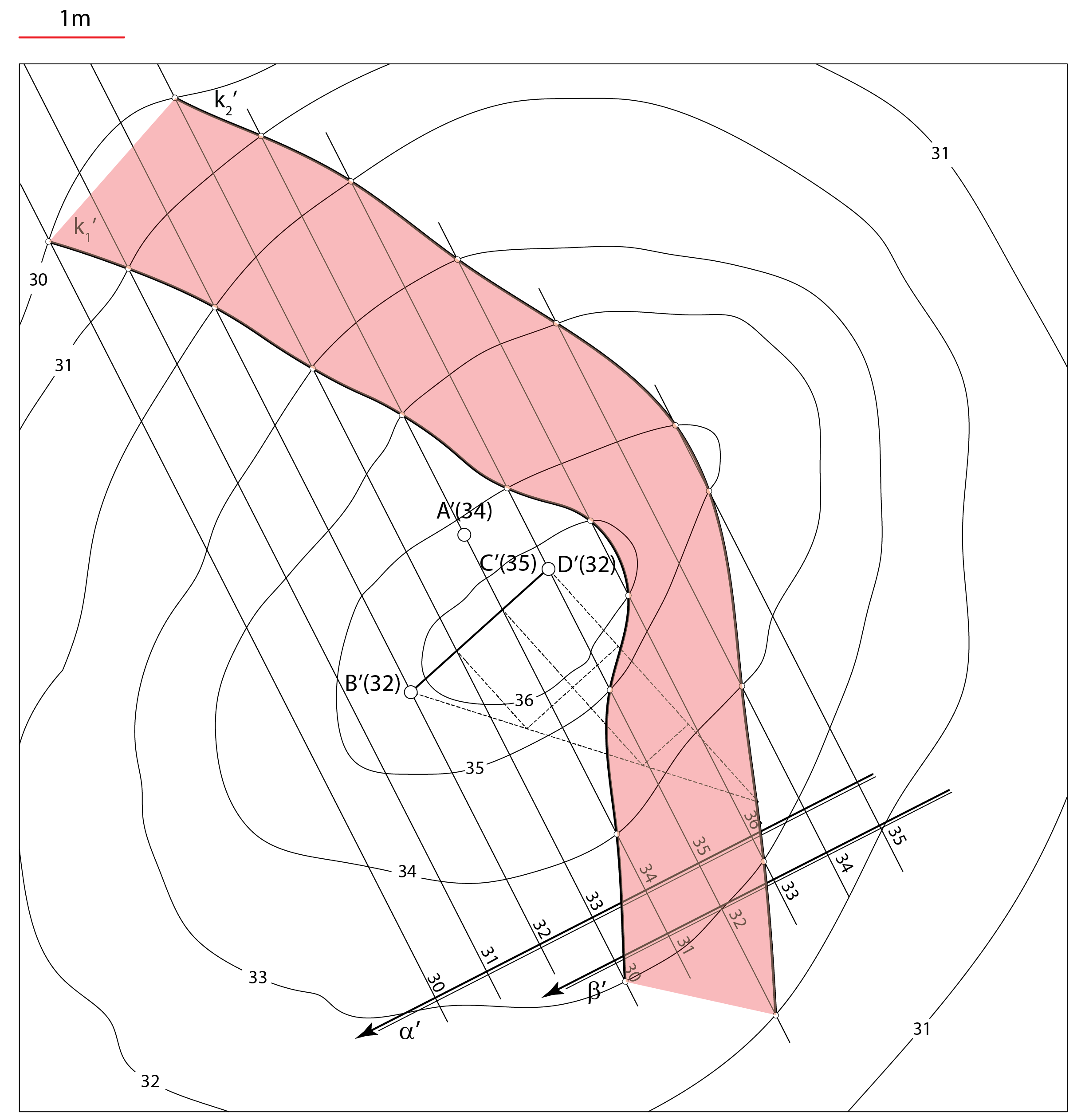
Na zadanom terenu krovinsku ravninu \(\small \alpha\) određuju tri bušotine
(točke \(\small A\), \(\small B\), \(\small C\)). Podinska
ravnina \(\small \beta\) određena je četvrtom bušotninom ispod jedne od tri zadane bušotine (npr. točka
\(\small D\) ispod točke \(\small C\)), slika 254.
|
 Slika 254 |
Opis konstrukcije:
|
Primjer 1: Na zadanom terenu \(\small \Phi\) krovinsku ravninu \(\small \alpha\) određuju tri bušotine
(točke \(\small A\), \(\small B\), \(\small C\)) kojima su zadani položaji projekcijom i kotom. Podinska
ravnina \(\small \beta\) određena je četvrtom bušotninom \(\small D\) (ispod bušotine \(\small C\)). Odredite sljedeće:
|



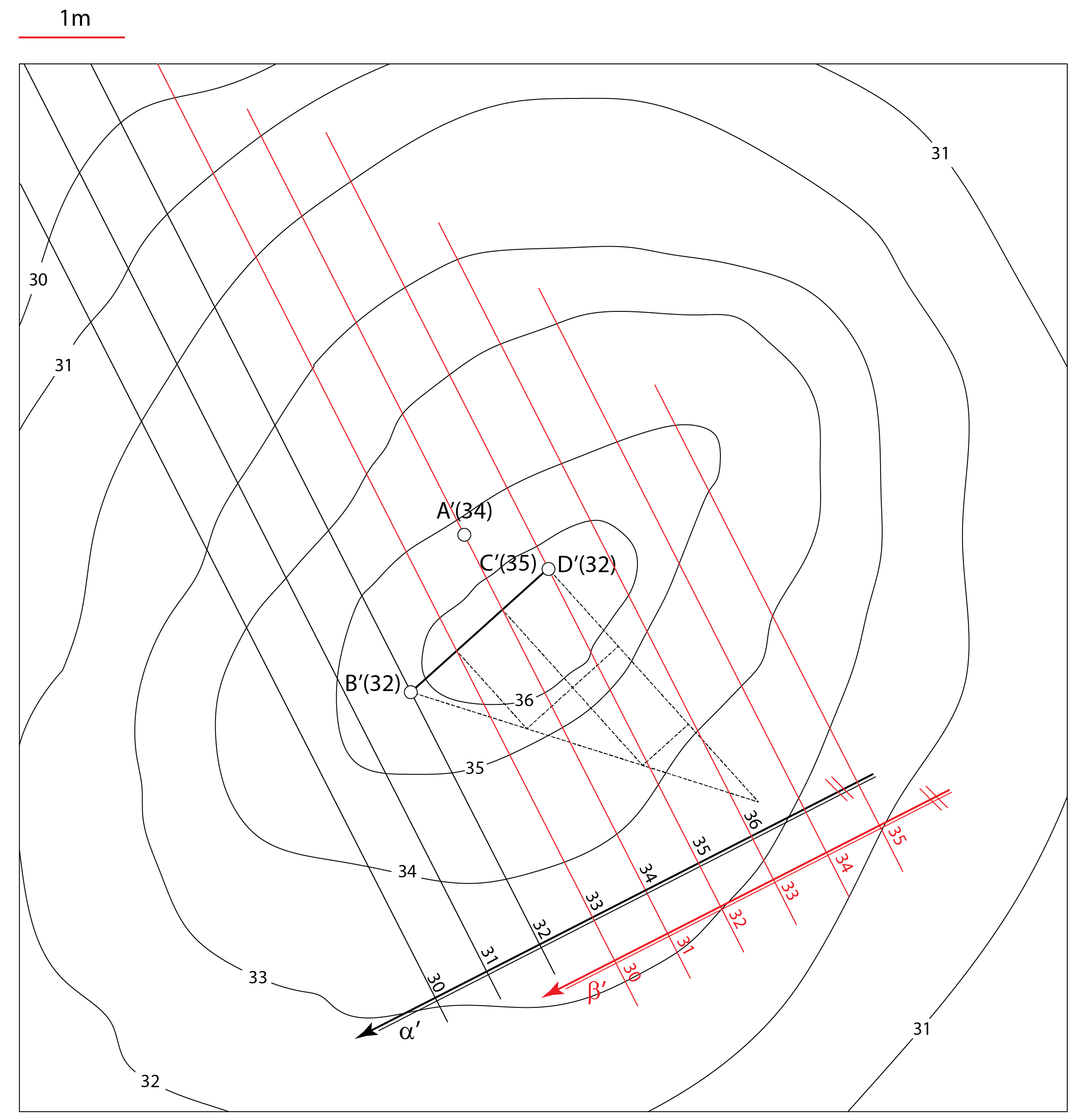

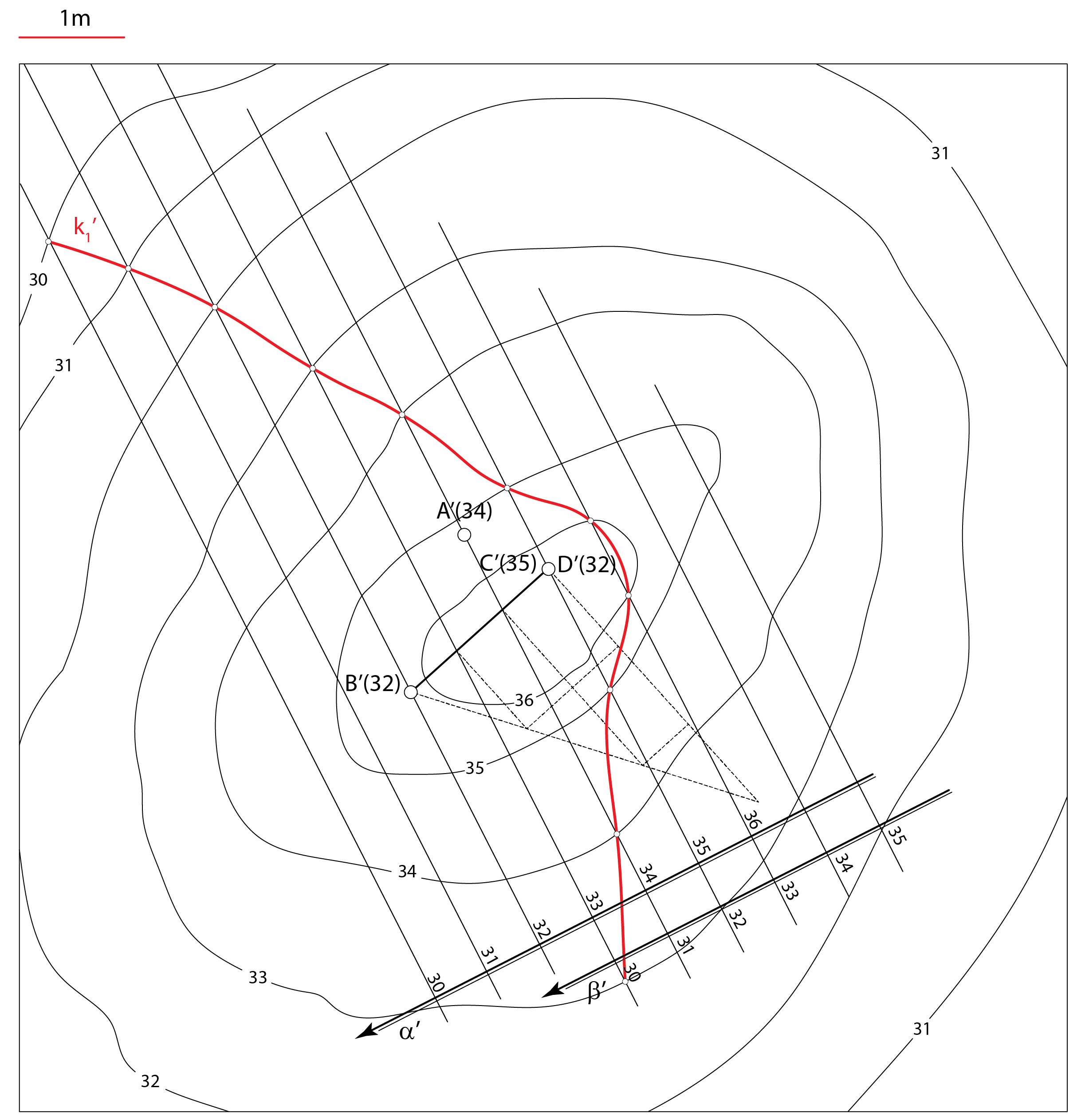
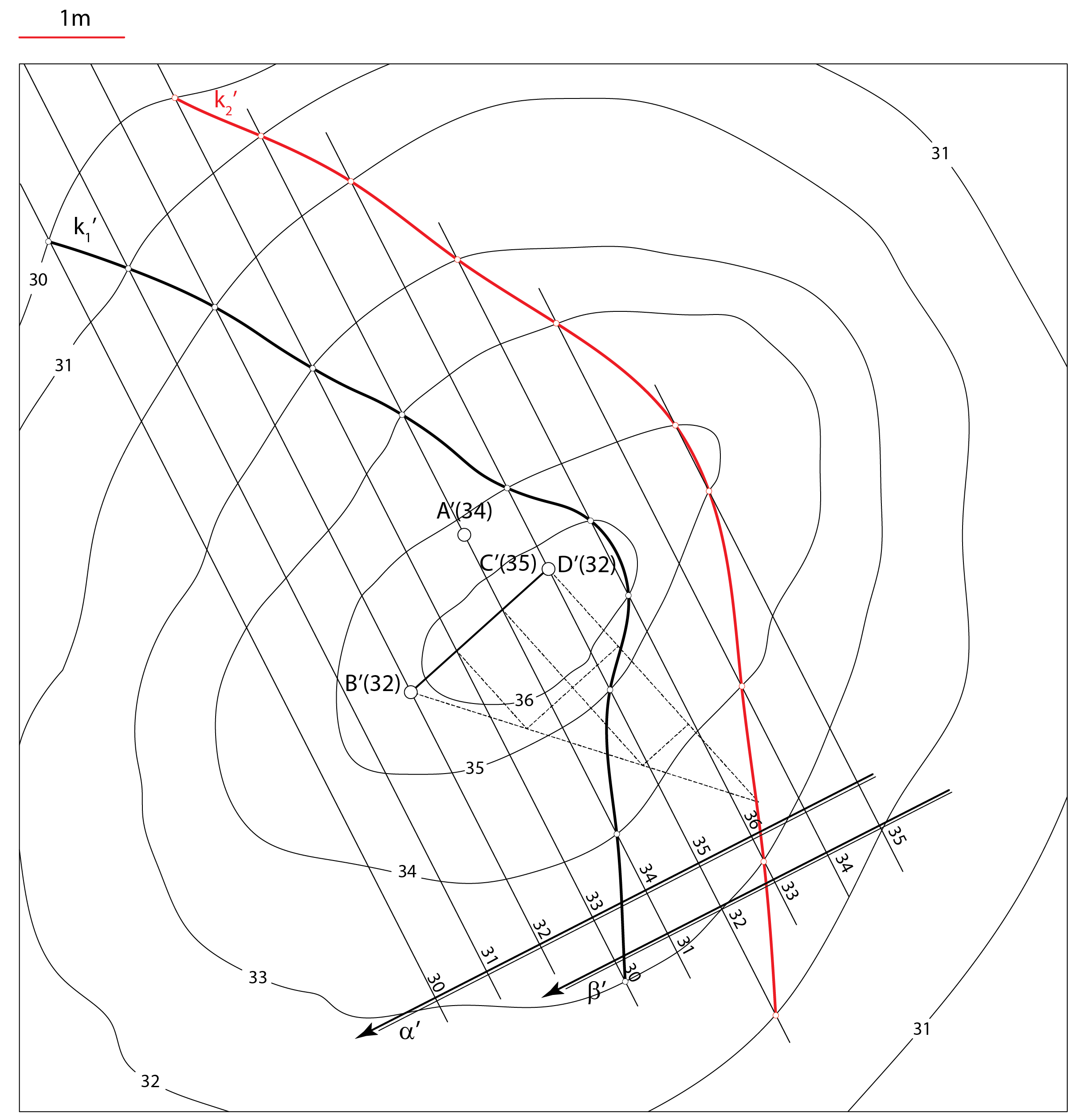
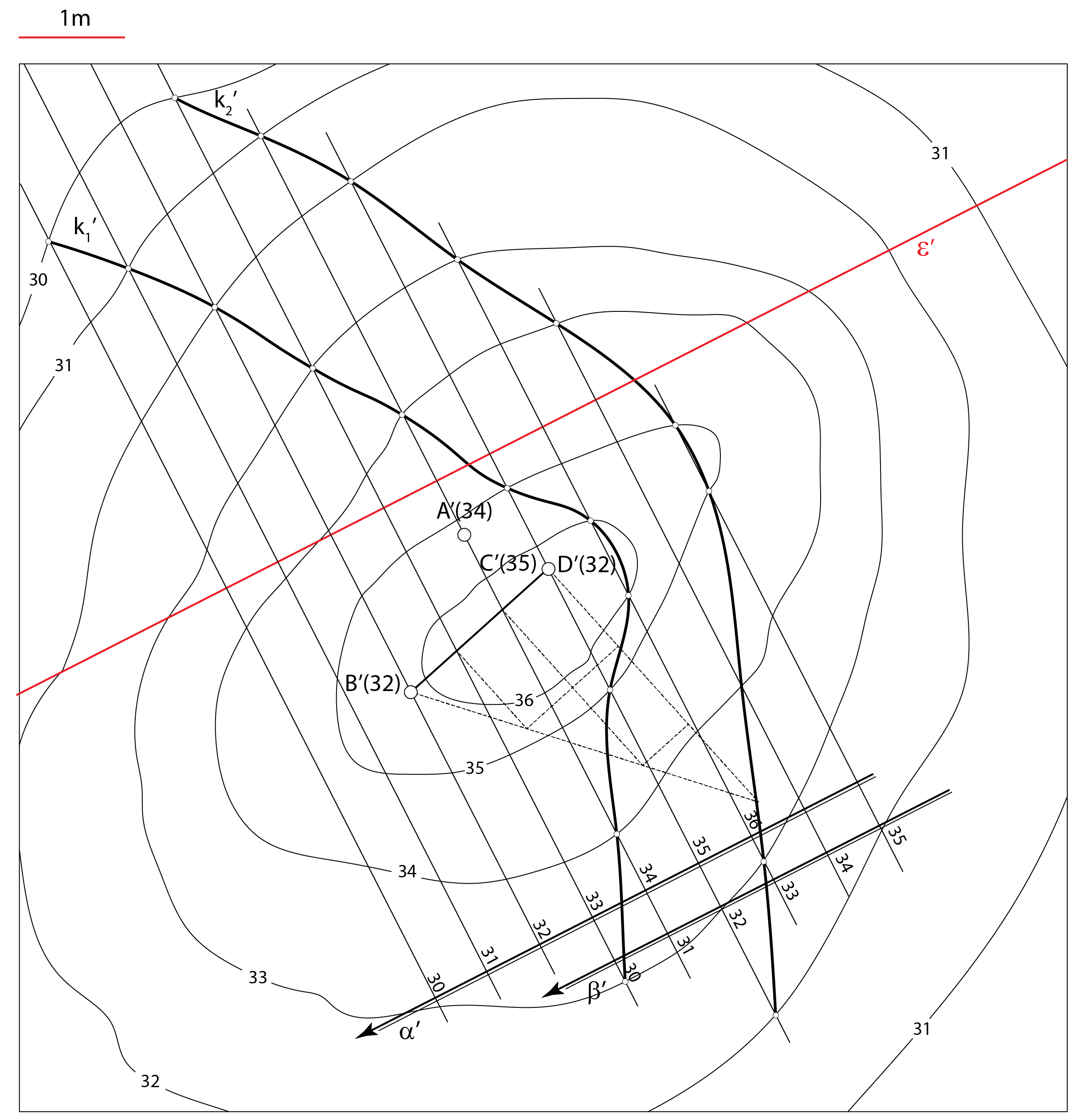




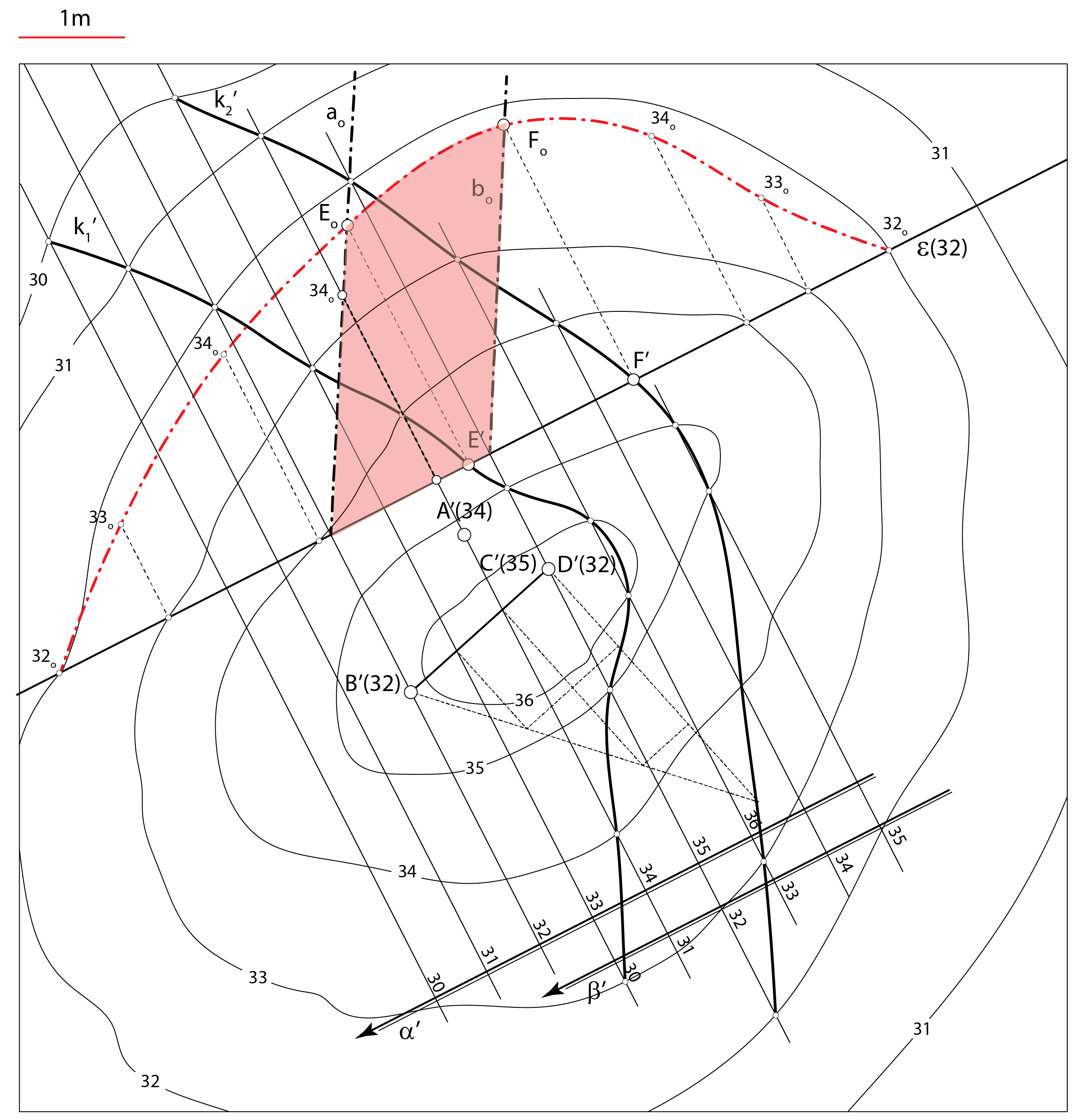

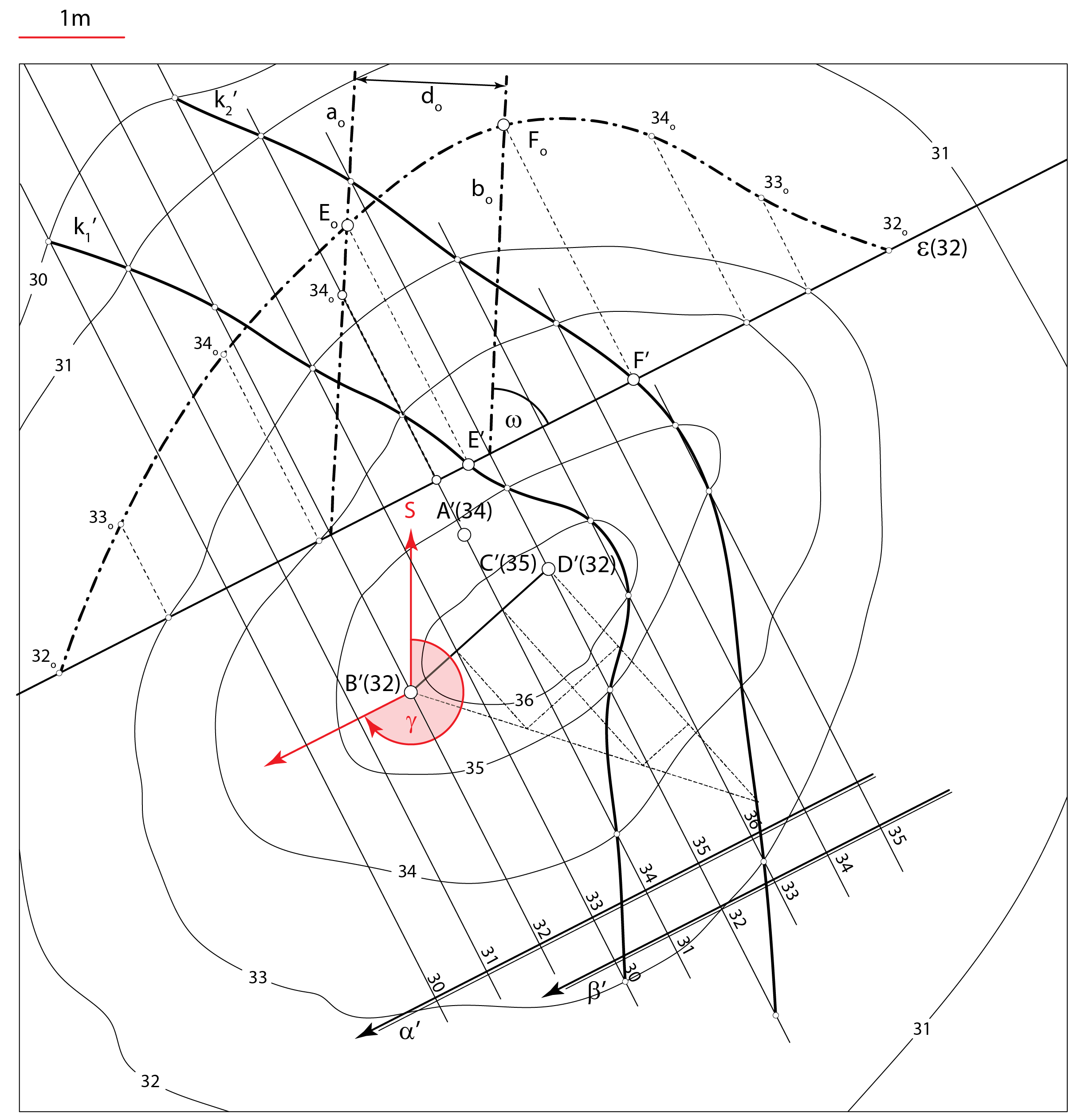
Prezentacija 59: Konstrukcija rješenja |
|
 Slika 255: Rješenje |
|
Na zadanom terenu krovinsku ravninu \(\small \alpha\) određuje jedna bušotina (točka \(\small A\))
te kutovi \(\small \gamma\) i \(\small \omega\). Podinska ravnina \(\small \beta\) određena je debljinom sloja \(\small d\).
Opis konstrukcije:
Primjer 2: Na zadanom terenu \(\small \Phi\) krovinsku ravninu \(\small \alpha\) određuje jedna bušotina (točka \(\small A\)), čiji je položaj određen projekcijom i kotom, te kutovi \(\small \gamma=150^\circ\) i \(\small \omega=45^\circ\). Debljina sloja \(\small d\) je 3 metra. Odredite sljedeće:
|

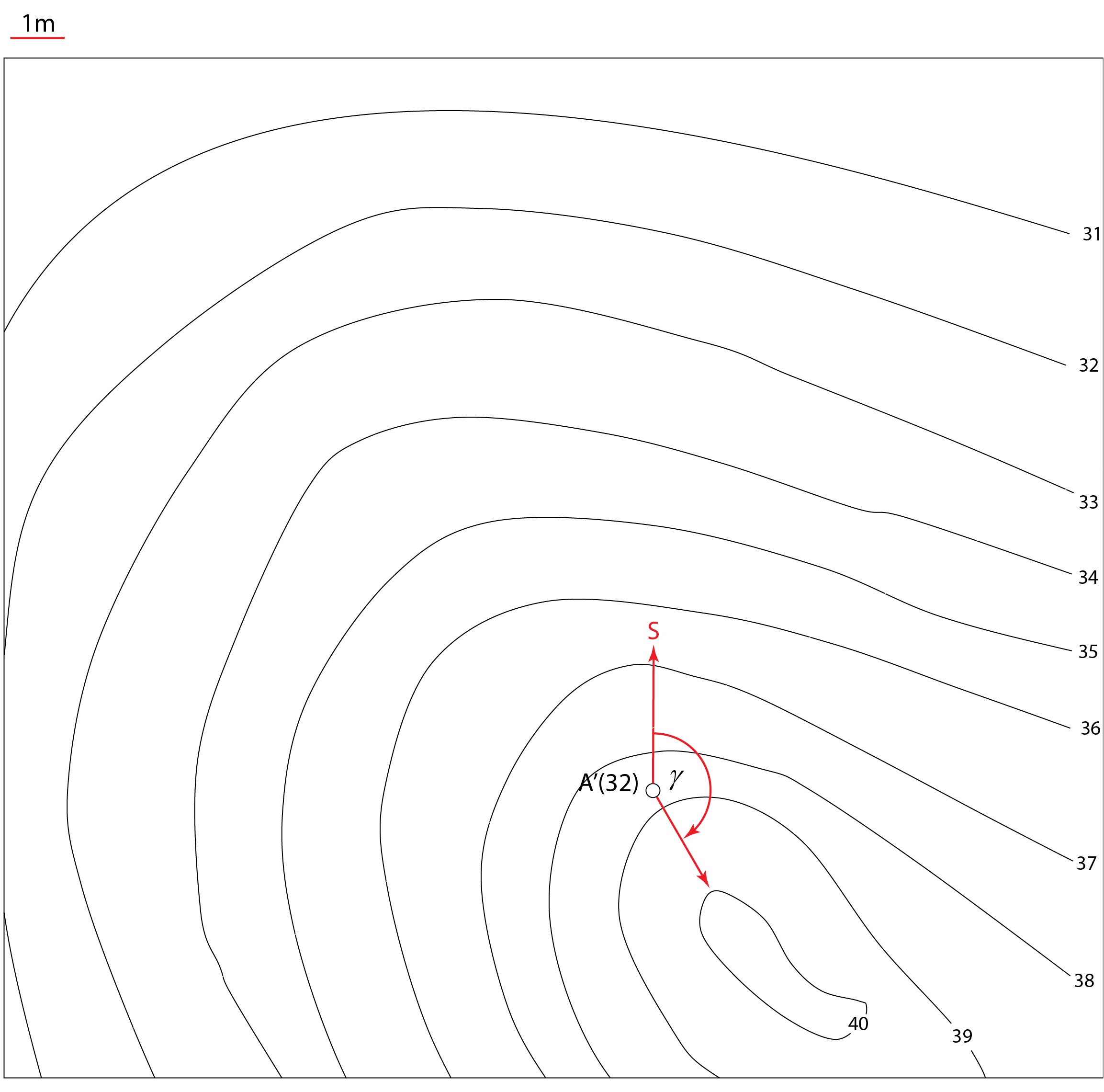
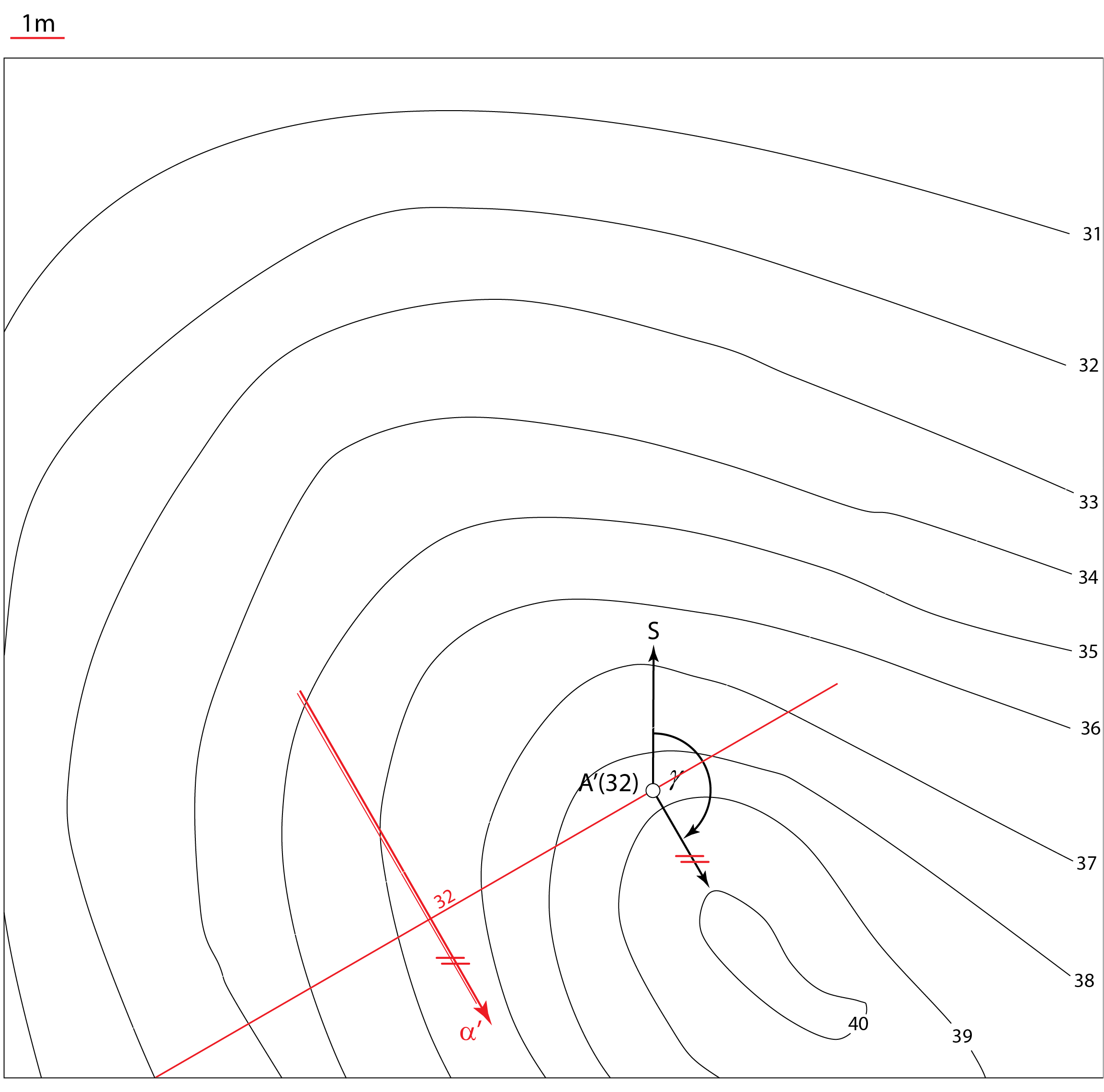
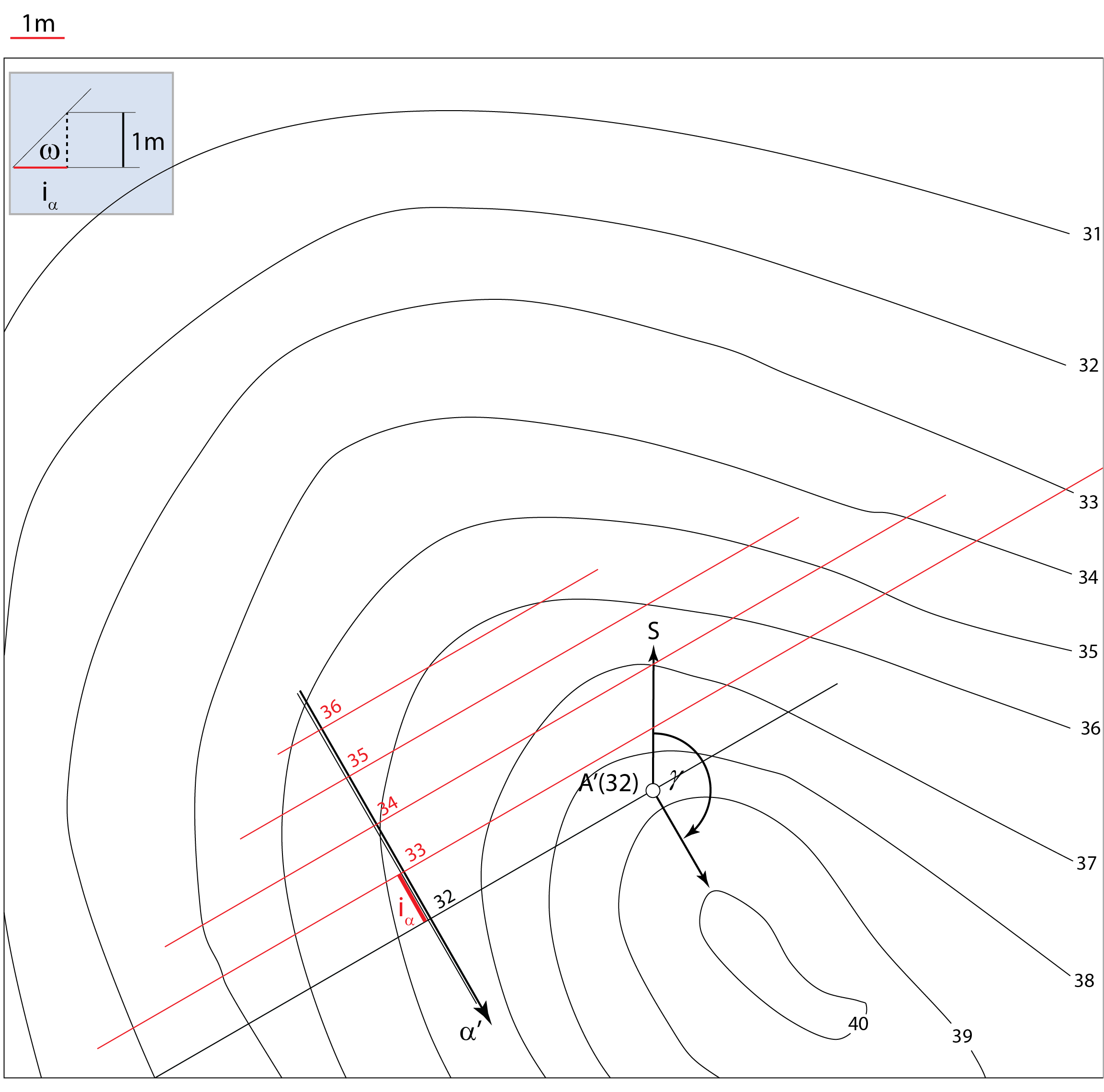





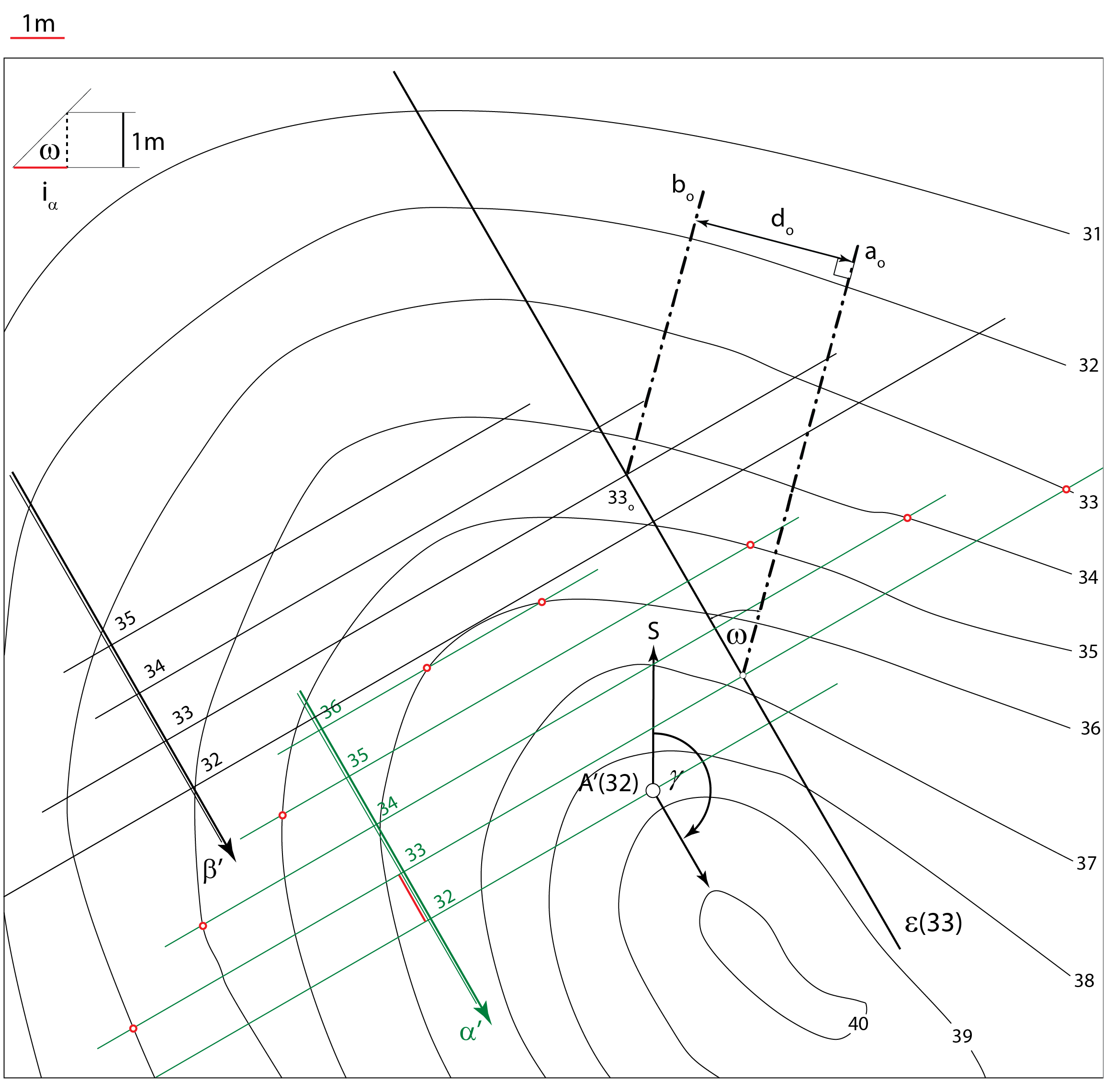
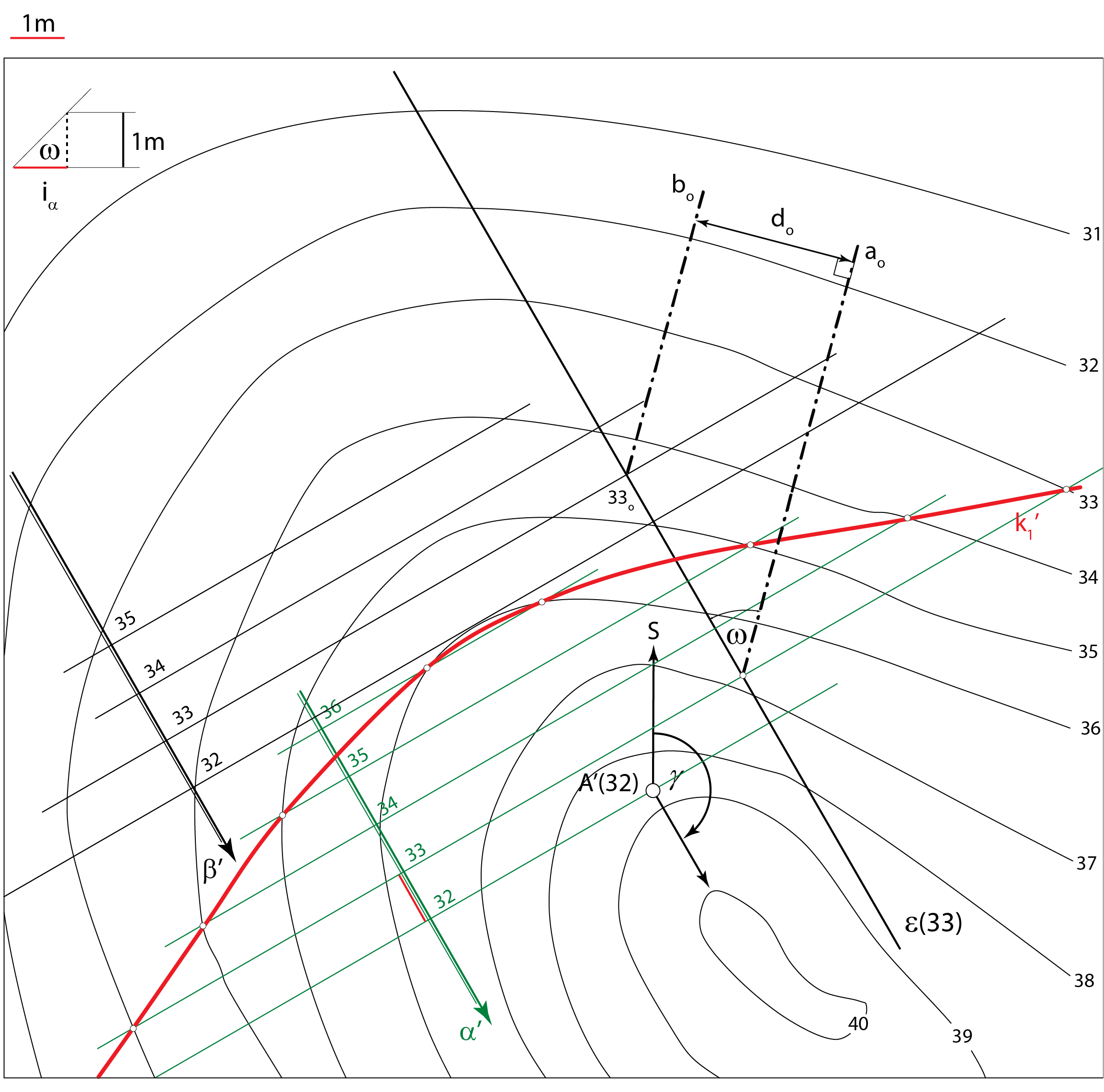

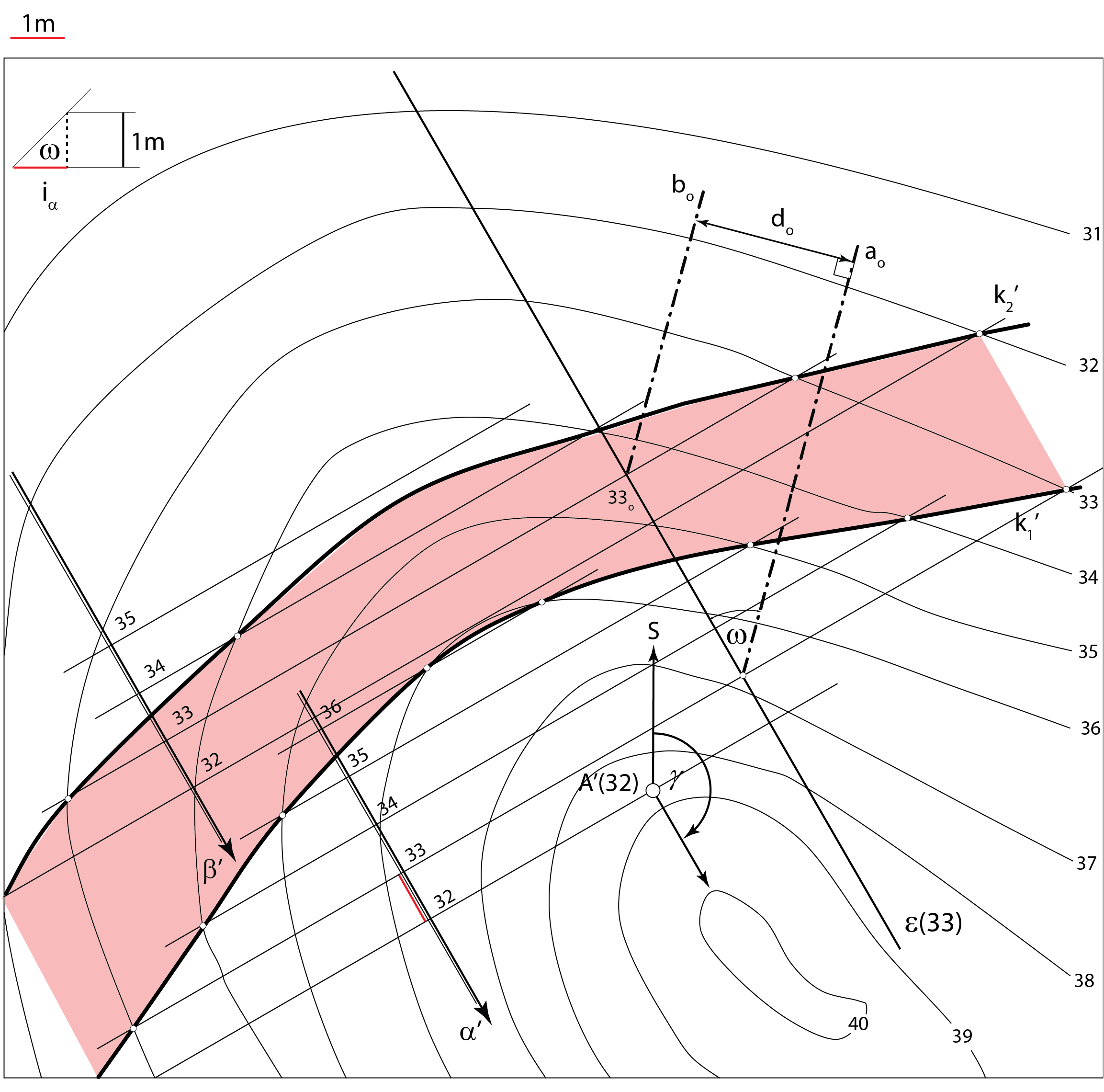

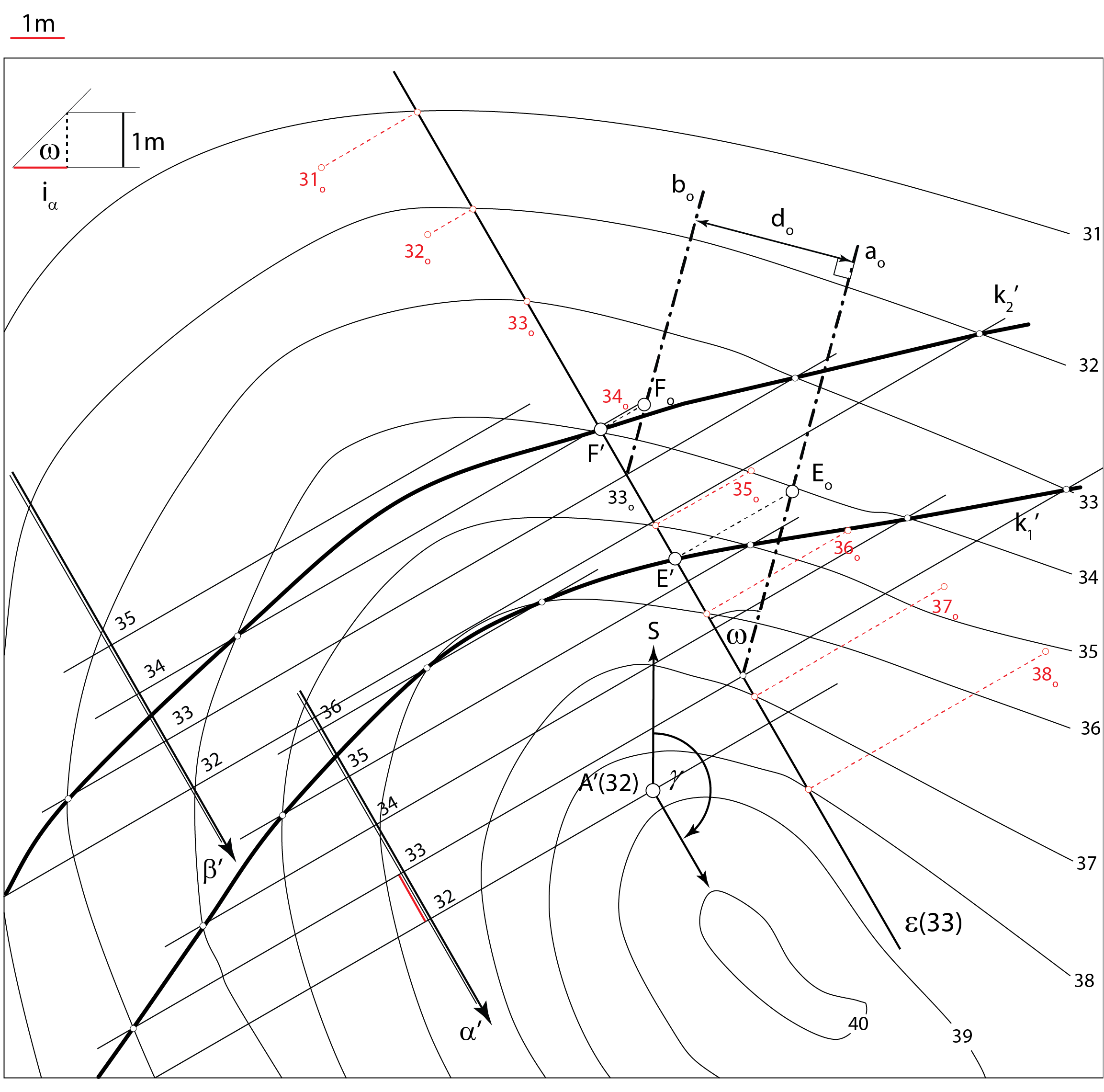
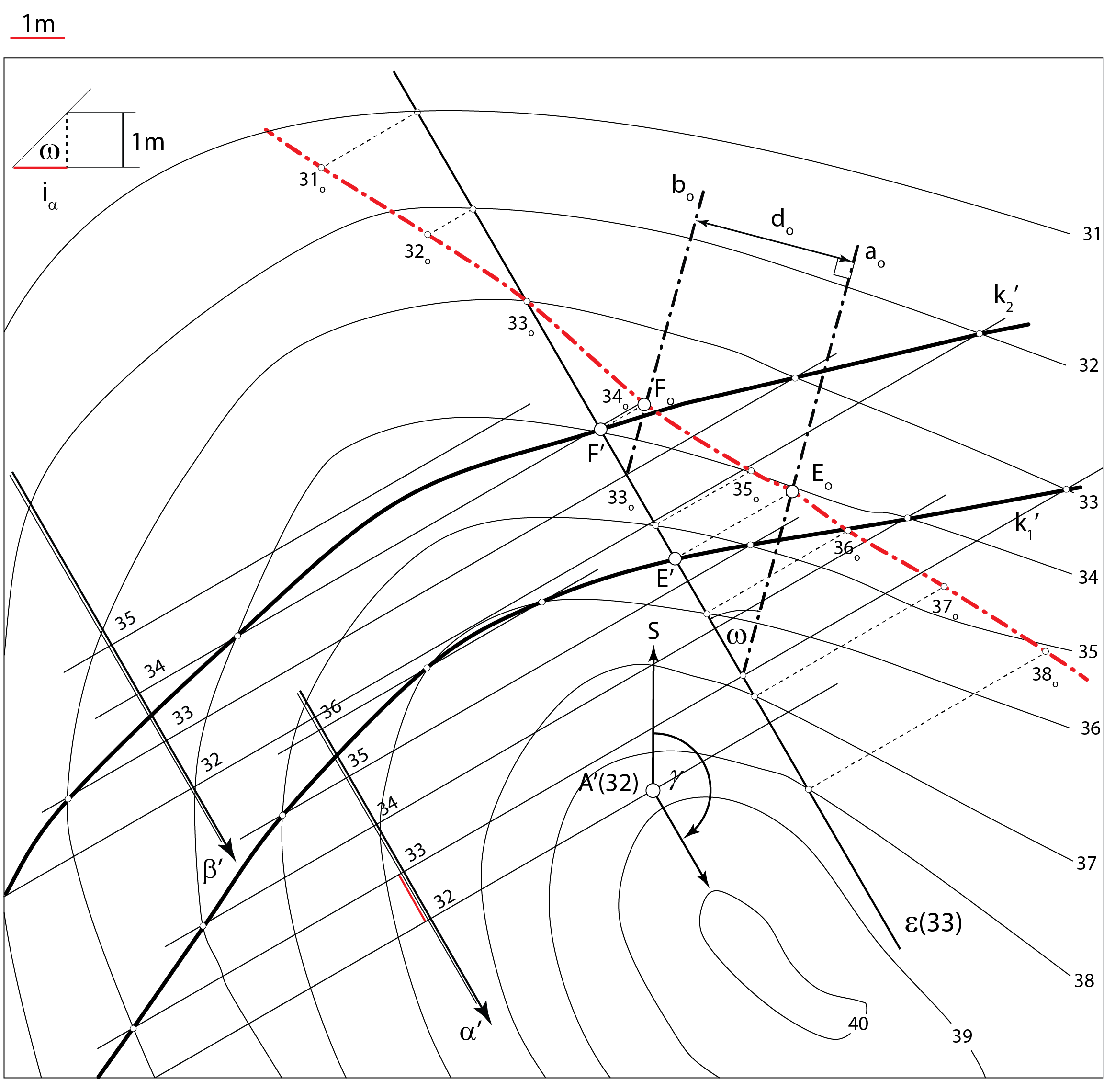

Prezentacija 60: Konstrukcija rješenja |
|
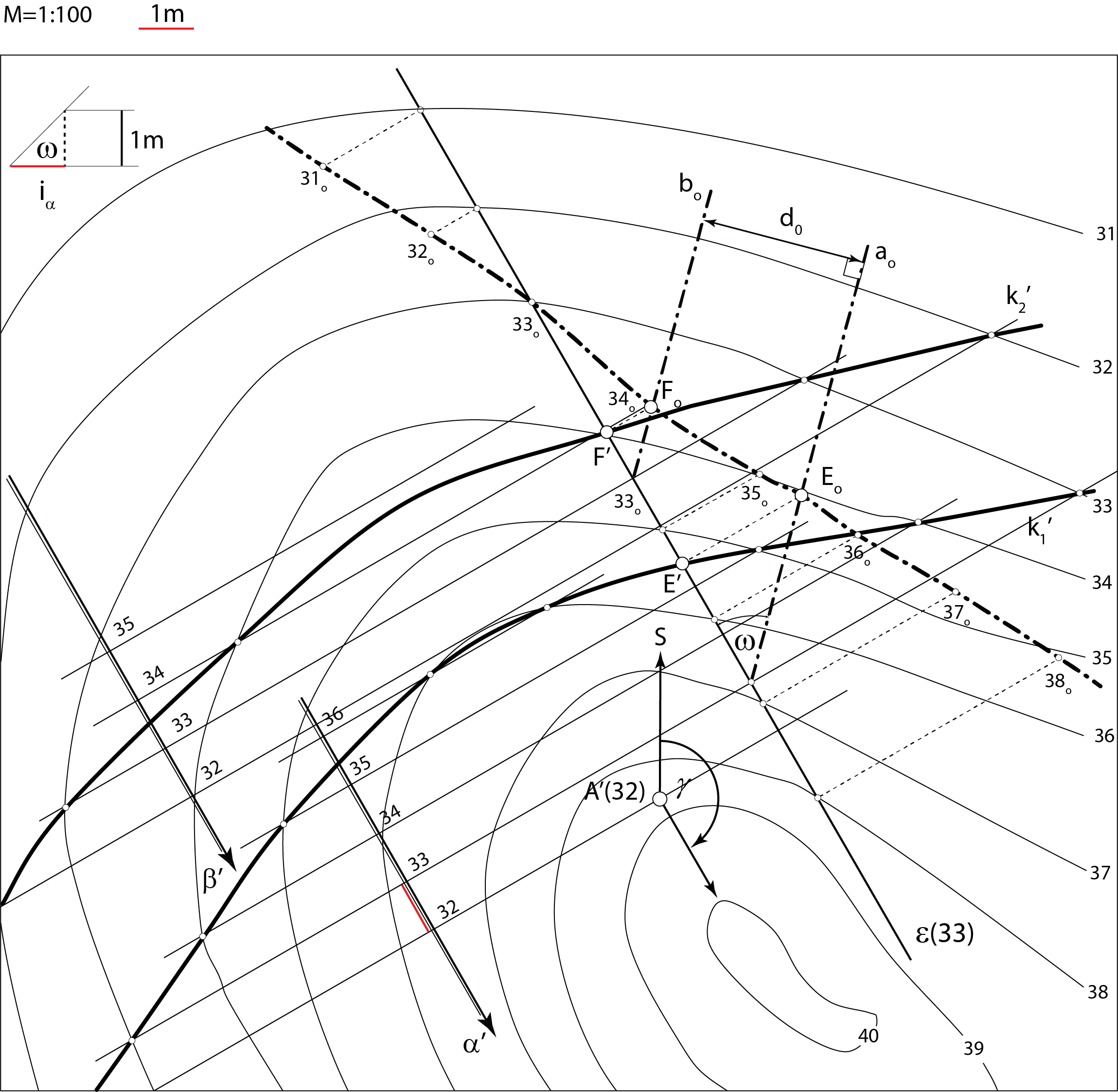 Slika 256: Rješenje |
Sonja Gorjanc i Ema Jurkin - DESKRIPTIVNA GEOMETRIJA