1.2.2. Klasifikacija i razred konika

Na pravim krivuljama 2. reda, onima koje nisu raspadnute, nema dvostrukih točaka. Naime, izraz \(\small (n-1)(n-2)/2\) poprima vrijednost \(\small 0\) za \(\small n=2\). Ako dvostruka točka postoji, krivulja se raspada na dva pravca koji mogu biti realni i različiti, realni koji se podudaraju ili par konjugirano imaginarnih pravaca koji se sijeku u jednoj realnoj točki. U okviru našega nastavnog predmeta bavit ćemo se uglavnom pravim krivuljama 2. reda koje nazivamo konikama i o kojima ste već dosta doznali tijekom prijašnjeg školovanja. To su elipse (koje kao poseban slučaj sadrže kružnice), hiperbole i parabole.

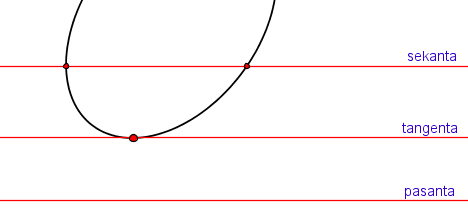
Slika 4

Svaki pravac ravnine neke konike ima s tom konikom dvije zajedničke točke. Ako su točke realne i različite, kažemo da je pravac sekanta konike. Ako se dvije zajedničke točke pravca i konike podudaraju, kažemo da je pravac njezina tangenta, a ako su zajedničke točke konjugirano imaginarne onda kažemo da je pasanta konike.

Želimo li izbjeći spominjanje konjugirano imaginarnih točaka (koje ne možemo grafički prikazati) možemo reći da je sekanta pravac koji koniku siječe u dvije točke, tangenta ju dodiruje u jednoj točki, a pasanta nema s konikom zajedničkih točaka, vidi sliku 4.



Interaktivna slika 3

Beskonačno daleki pravac ravnine na kojem leže realne beskonačno daleke točke svih ostalih realnih pravaca ravnine također ima dvije zajedničke točke sa svakom konikom svoje ravnine. Konike se i dijele na gore navedene tipove upravo prema vrsti njihovih sjecišta s beskonačno dalekim pravcem:

  • Hiperbole su konike koje beskonačno daleki pravac njihove ravnine siječe u dvije realne i različite točke i zapravo je beskonačno daleki pravac sekanta hiperbole. Asimptote hiperbole su njezine tangente u tim beskonačno dalekim točkama.

  • Parabole su konike koje beskonačno daleki pravac njihove ravnine dodiruje u jednoj točki, odnosno beskonačno daleki pravac je tangenta svake parabole. Beskonačno daleko diralište leži na osi parabole.

  • Elipse su konike koje na beskonačno dalekom pravacu imaju par konjugirano imaginarnih točaka, pa je beskonačno daleki pravac pasanta elipse. Kružnica je elipsa koja prolazi posebnim parom konjugirano imaginarnih točaka beskonačno dalekog pravca. Ta imaginarna sjecišta kružnice i beskonačno dalekog pravca njezine ravnine nazivamo apsolutnim točkama ravnine.
Pomičite točke \({\small X}\) na interaktivnoj slici 4.

Interaktivna slika 4

Interaktivna slika 4 samo je ilustracija navedenih svojstava konika budući da se realni beskonačno daleki elementi ne mogu nacrtati, iako se relativno jednostavno mogu zamisliti. Za razliku od njih, imaginarne elemente teško je i zamisliti u realnoj ravnini. Zašto ih onda ovdje uopće spominjemo? Zato što imaginarni elementi utječu na osobine realnih dijelova krivulja, a ti nas dijelovi zanimaju. Pokušajte, primjerice, odgovoriti na pitanje: Zašto dvije kružnice mogu imati najviše dvije realne zajedničke točke?

Interaktivna slika 5

Osim prema redu, ravninske se algebarske krivulje razvrstavaju i prema razredu.

  • Razred ravninske algebarske krivulje jednak je broju njezinih tangenata koje prolaze bilo kojom točkom ravnine krivulje.

Isto kao i presječne točke pravca i krivulje, tangente iz neke točke na krivulju mogu biti realne ili u parovima konjugirano imaginarne. Imaginarne je pravce možda i teže zamisliti nego imaginarne točke. Stoga ćemo samo ustvrditi da je konika krivulja 2. razreda, odnosno da je iz svake točke njezine ravnine moguće na koniku postaviti dvije realne i različite tangente ako točka leži u vanjštini (eksterioru) konike, realne i podudarne ako je točka na konici te konjugirano imaginarne ako točka leži u unutrašnjosti (interioru) konike. Za krivulje kojima su red i razred jednaki kažemo da imaju stupanj koji je jednak njihovu redu i razredu. Stoga su konike krivulje 2. stupnja.

Pomičite točku \({\small X}\) na interaktivnim slikama 6, 7 i 8 te uočite područja točaka iz kojih su tangente na koniku realne ili pak konjugirano imaginarne. Na granici tih područja nalaze se točke konike u kojima je tangenta jedinstvena, a mi je, u smislu razreda konike, dva put brojimo.

Interaktivna slika 6 Interaktivna slika 7 Interaktivna slika 8


Parabola kao omotaljka tangenata - Primjer konstrukcije razredne krivulje (Slika 5, Prezentacija 1)




Sonja Gorjanc - GeomTeh3D - Razvojni projekt Sveučilišta u Zagrebu, izrađeno GeoGebrom