Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
8. vježbe

3D grafika

Graphics 3D

Zadatak 1.

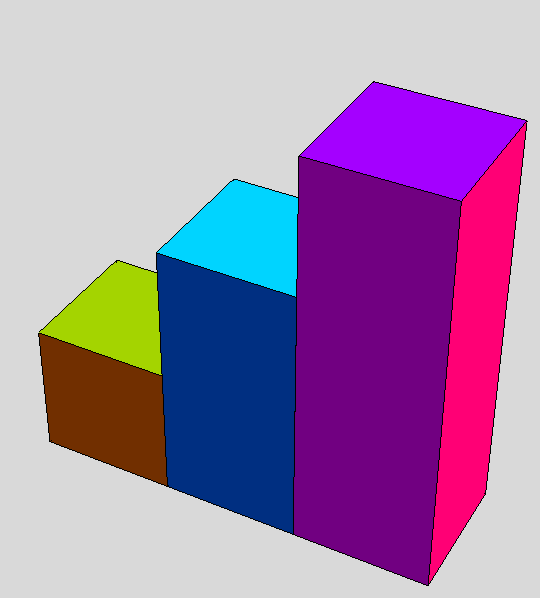
Plot3D

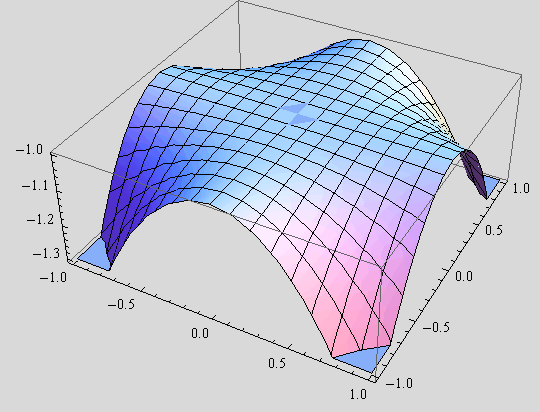
Zadatak 1

1.  Nacrtajte graf funkcije f(x,y)= –cosh(x·y) nad područjem .

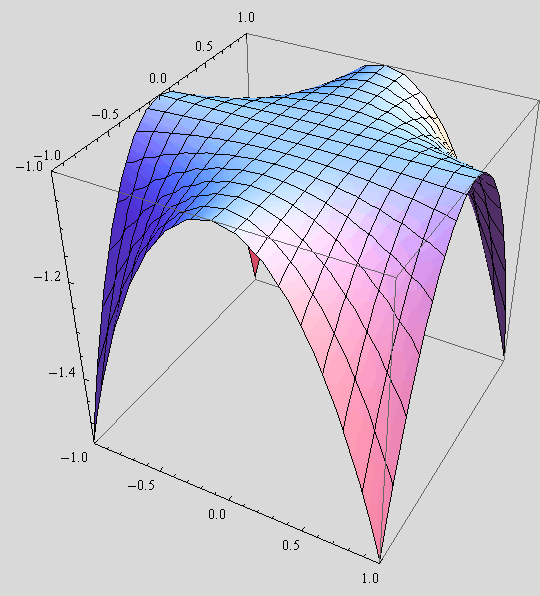
2. Pomoću opcija PlotRange i BoxRatios prikažite isti graf u okviru (–1,1)×(–1,1)×(–1.55,–1), s odnosom bridova 1:1:1.

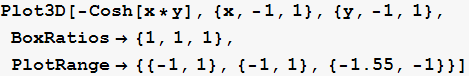
3. Nacrtajte sljedeći crtež.


Uputa: Koristite opciju Filling → Bottom.
Na žalost, to opciju ne podržavaju sve ostale funkcije za 3D grafiku.

Zadaci za vježbu

Zadatak 1.

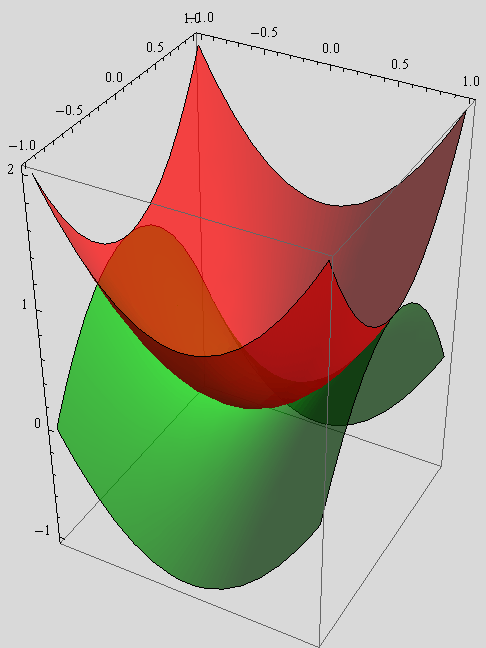
Na istoj slici, nad područjem , nacrtajte kružni i hiperbolički paraboloid.
Jednadžbe z = +  i  z = –.

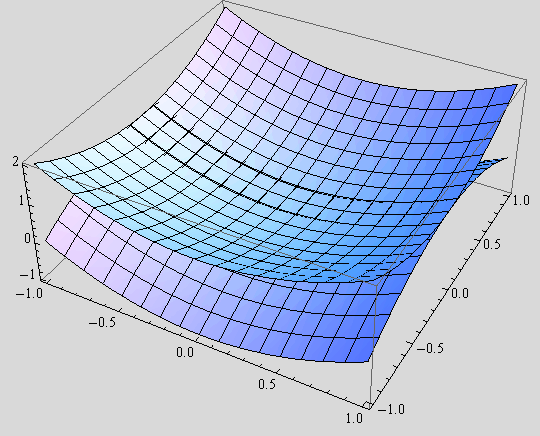
Iste plohe prikažite tako da kružni paraboloid bude crven, a hiperbolički zelen.
Neka prikazi ploha imaju 30% prozirnosti, a jedinice na osima neka budu jednake.

Zadatak 2.

Na istoj slici, nad područjem prikažite plohe zadane eksplicitnim jednadžbama
z = cosx cosy  i  z = sinx siny .
Obojite ih različitim bojama, a jedinice na osima neka budu jednake.

ParametricPlot3D

Zadatak 1.

a) Nacrtajte plohu kojoj su parametarske jednadžbe
    x(u,v) = sinu,
    y(u,v) = cosu+sinv,
    z(u,v) = cosv,    (u,v) ε .

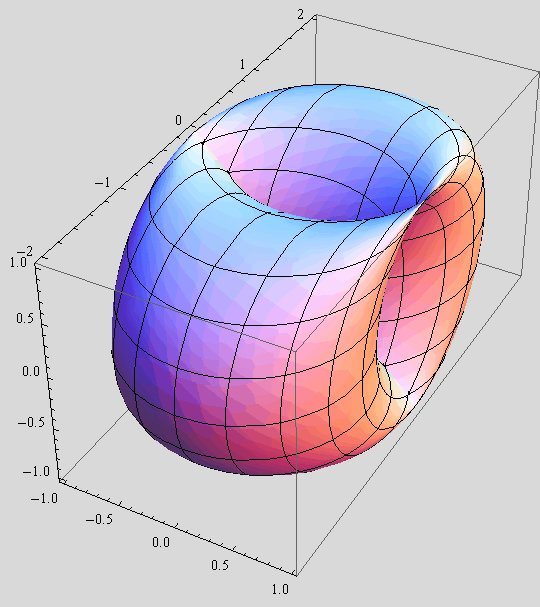
b) Istu plohu prikažite tako da je na njoj iscrtan samo jedan sistem njezinih parametarskih krivulja te da je prozirnost prikaza 30%.

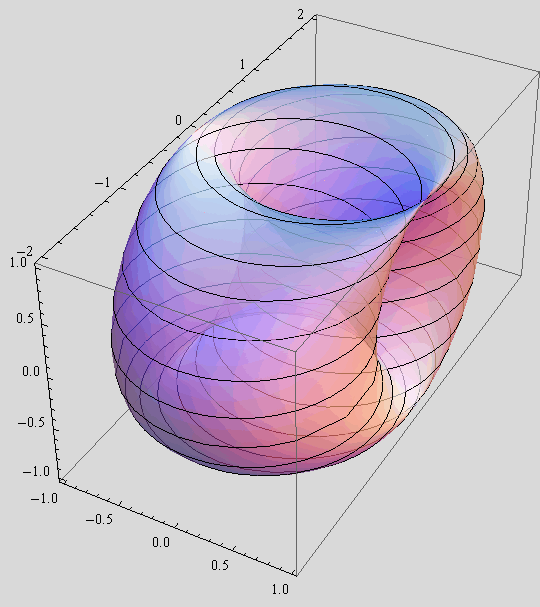
Zadatak 2.

a) Pomoću parametarskih jednadžbi nacrtajte kuglu sa središtem u ishodištu i polumjera 2.
Neka Mathematica pri tom ne iscrtava parametarske krivulje.
Pridružite taj crtež varijabli kugla.

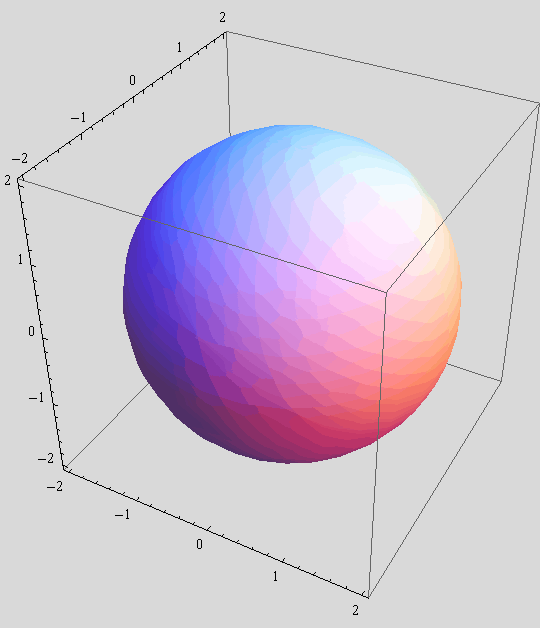
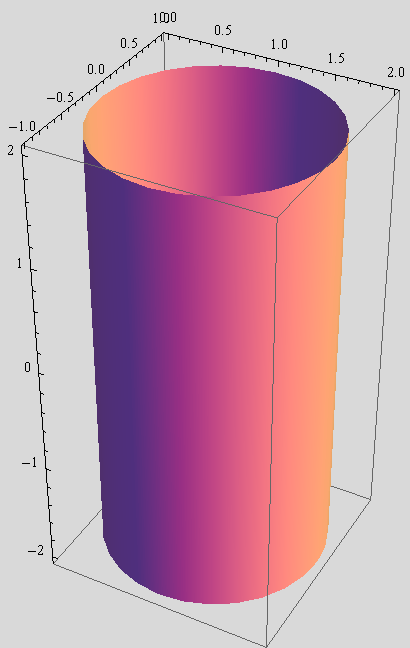
b) Nacrtajte plašt valjka kojem je dužina MN [M(1,0,-2),N(1,0,2] os, a polumjer osnovice r = 2.
Neka Mathematica pri tom ne iscrtava parametarske linije na plaštu.
Pridružite taj crtež varijabli valjak.

Uputa: Parametarske jednadžbe tog plašta su
    x = cosu +1,
    y = sinu,
    z = z,    (u,z) ε [0,2π]×[-2, 2].

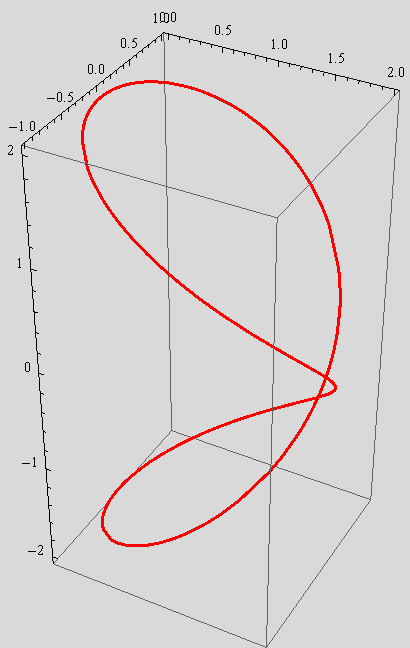
c) Nacrtajte krivulju kojoj su parametarske jednadžbe
    x(t) = 1+cost,
    y(t) = sint,
    z(t) = 2sin,    tε[–2π,2π].
Obojite ju crveno i podebljajte.
Pridružite taj crtež varijabli viviani (tu krivulju nazivamo Vivianijevom).

d) Pomoću fukcije Show pokažite da je Vivianijeva krivulja prodorna krivulja gornjih ploha, tj. prikažite crteže kugla, valjak i viviani na istoj slici.

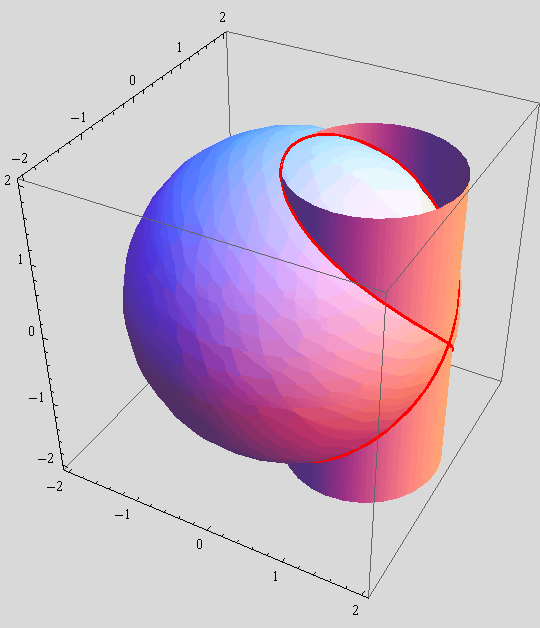
Zadatak 3.

a) Definirajte funkciju jastuk[i_] kao listu sljedećih parametarski jednadžbi:
    x(u,v) = sinu,
    y(u,v) = sinv,
    z(u,v) = i cosu cosv.    

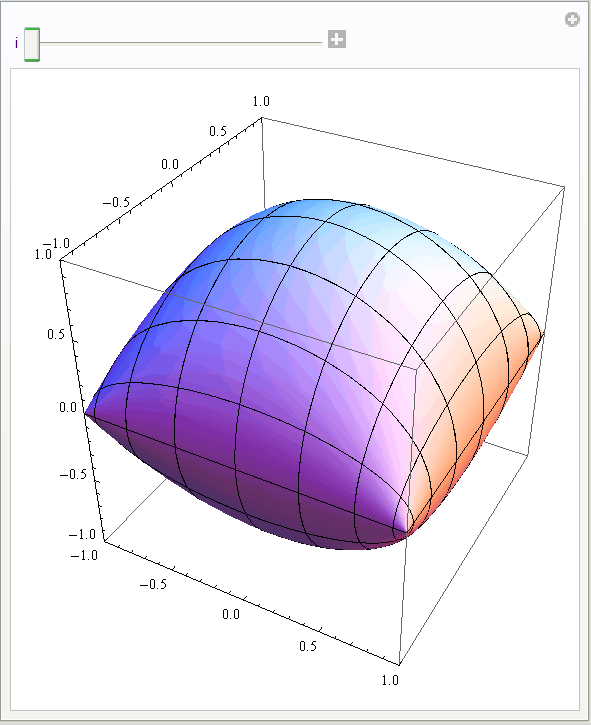
b) Pomoću funkcije Manipulate prikažite kako se za područje (u,v) ε mijenja gornja ploha, ako parametar i poprima vrijednosti na intervalu  [-1, 1].
Neka je "finoća" plohe određena opcijom PlotPoints→40, a PlotRange→{{-1,1},{-1,1},{-1,1}}.

Zadaci za vježbu

Zadatak 1.

Torus je ploha koja nastaje rotacijom kružnice polumjera oko osi koja je od njezinog središta udaljena za .
Ako kružnica leži u ravnini xz i rotira oko osi z, parametarske jednadžbe torusa su:
    x(u,v) = (+·cosv) cosu,
    y(u,v) = (+·cosv) sinu,
    z(u,v) = ·sinv,    (u,v)ε.

a) Definirajte funkciju torus1, koja ovisi o vrijednostima i , a jednaka je listi gornjih funkcija {x(u,v), y(u,v), z(u,v)}.

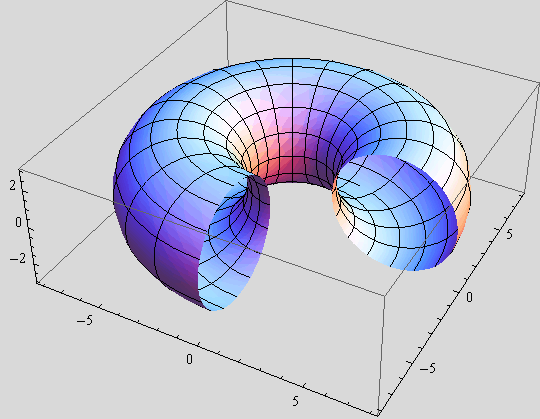
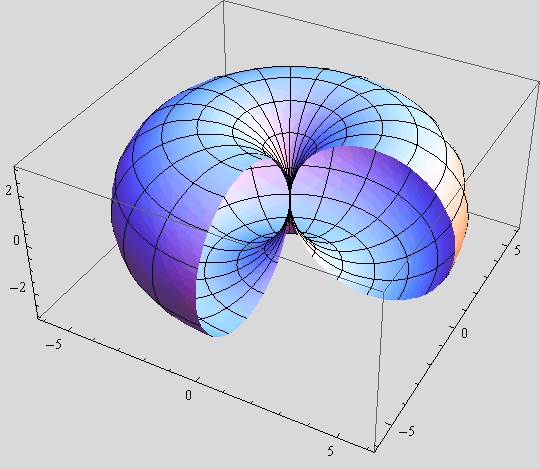
b) Za = 3 nacrtajte 3 takve plohe ( = 5, 3, 1) nad područjem [0,]×[0,2π].

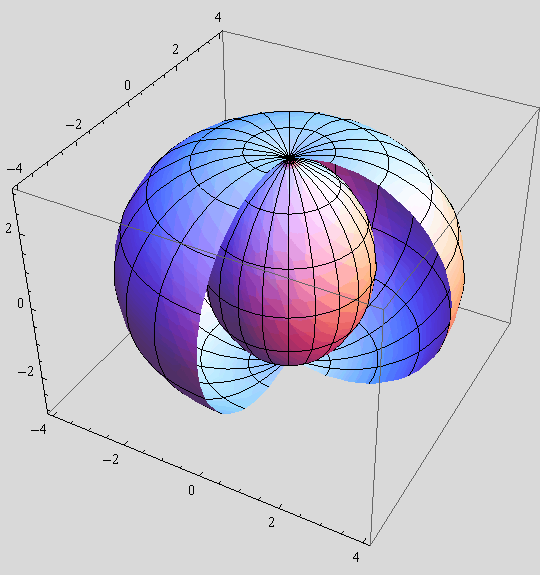
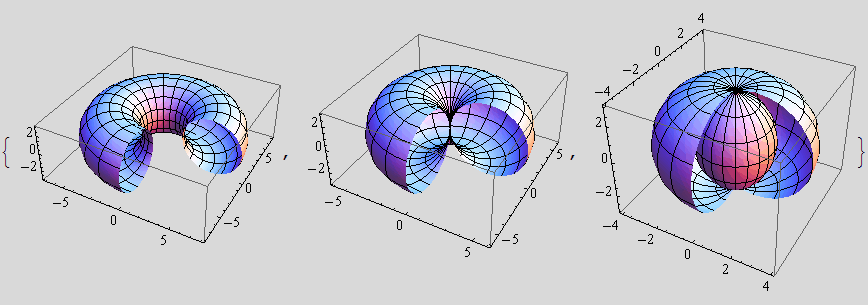
Zadatak 2.

Plückerovi konoidi su pravčaste plohe (jedan sistem parametarsih krivulje tih su pravci) koje zadovoljavaju sljedeće parametarske jednadžbe:
    x(u,v) = v cosu,
    y(u,v) = v sinu,
    z(u,v) = 3 sin kv,    k ∈ N,    (u,v) ∈ .
    

a) Definirajte funkciju plucker, koja ovisi o prirodnom broju k, a jednaka je listi gornjih funkcija {x(u,v), y(u,v), z(u,v)}.

b) Nacrtajte 4 Plückerova konoida za k = 2, 3, 4 i 5.

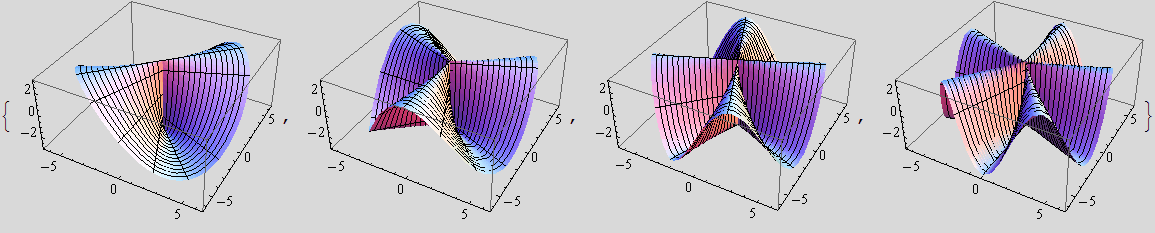
c) Nacrtajte Plückerov konoid, za k = 3, i neka Mathematica  iscrta samo one njegove parametarske krivulje koje su pravci.

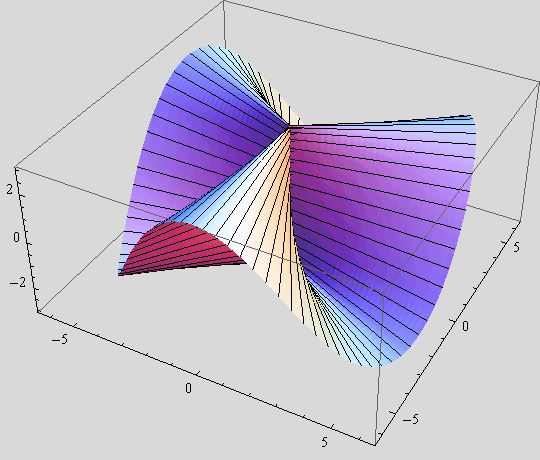
Zadatak 3.

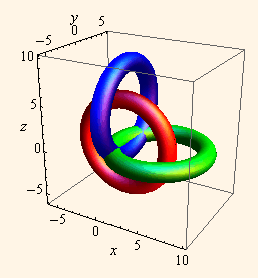
Ako u parametarskim jednadžbama torusa iz zadatka 1 izvršimo zamjenu  z↔y ( z↔x ) dobit ćemo parametarske jednažbe torusa kojem  se rotacijska os podudara s osi y (x).

a) Definirajte funkcije torus2 i torus3, koje su jednake listama parametarskih jednadžbi torusa s osima rotacije y, odnosno x.

b) Pomoću funkcija torus1, torus2 i torus3, nacrtajte sljedeće crteže.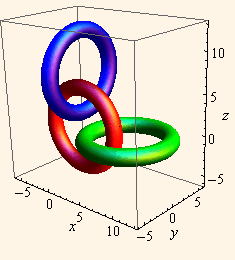

ContourPlot3D

Zadatak 1.

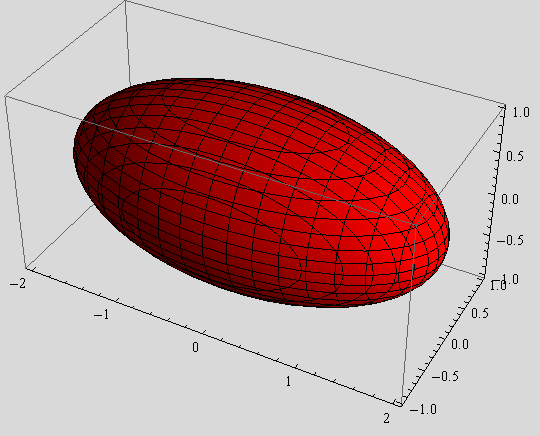
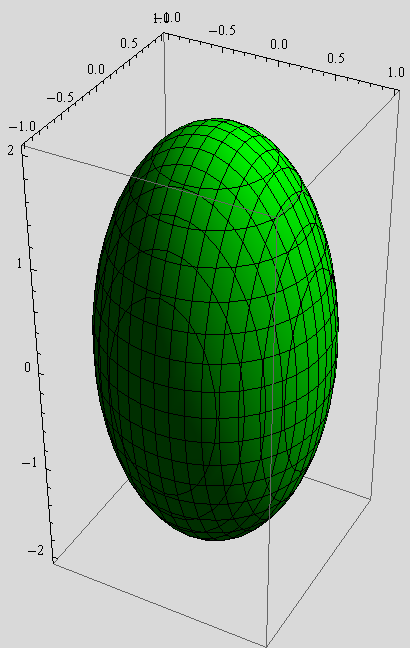
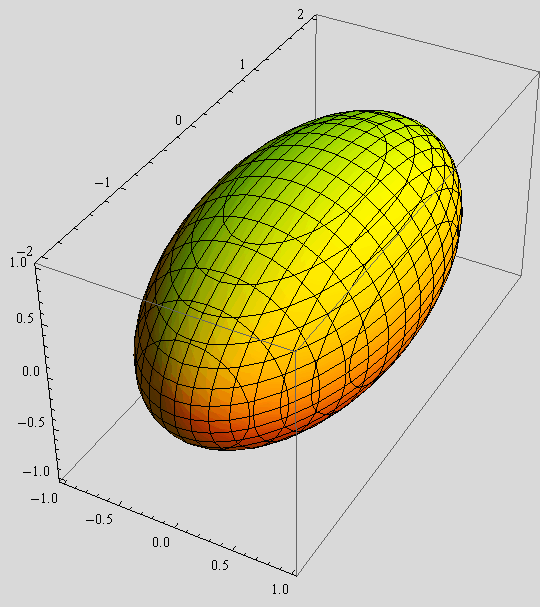
Nacrtajte elipsoide zadane jednadžbama
     + + = 1,  
     + + = 1
     + + = 1,
obojite ih redom crveno, zeleno i žuto, a zatim ih, pomoću funkcije Show, prikažite na istoj slici.

Uputa: Upotrijebite opciju BoxRatios→Automatic. Zašto je to potrebno?

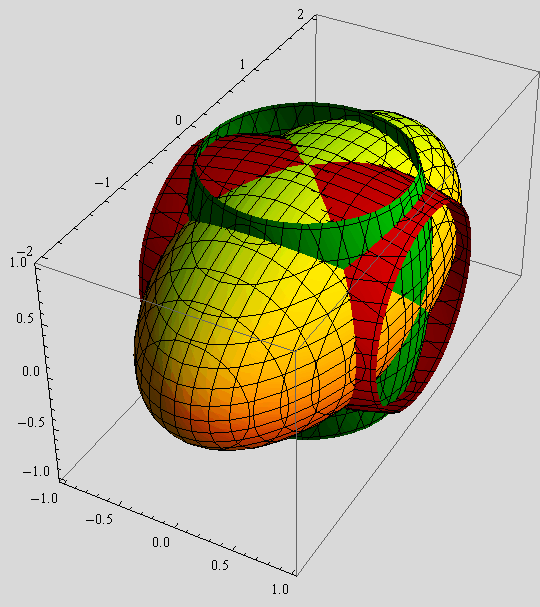
Zadatak 2.

a) Prikažite plohu zadanu jednadžbom + + = 1, unutar kocke .

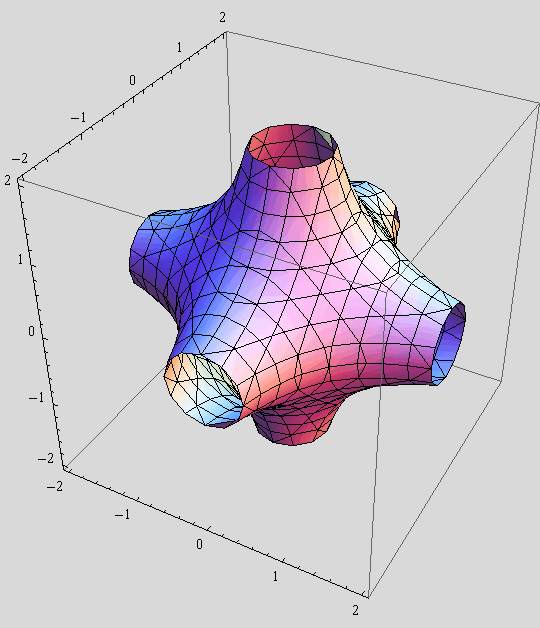
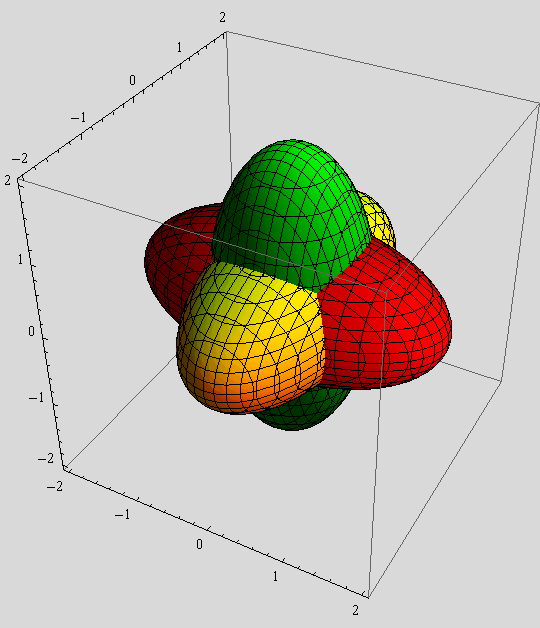
b) Istu plohu prikažite unutar kocke , obojite ju narandžasto, te na njoj iscrtajte presjeke plohe s koordinatnim ravninama. Pomoću opcije PlotPoints generirajte finiji prikaz nego u slučaju a).

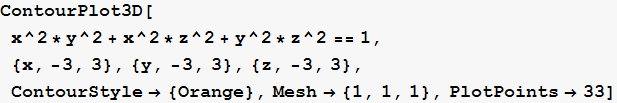
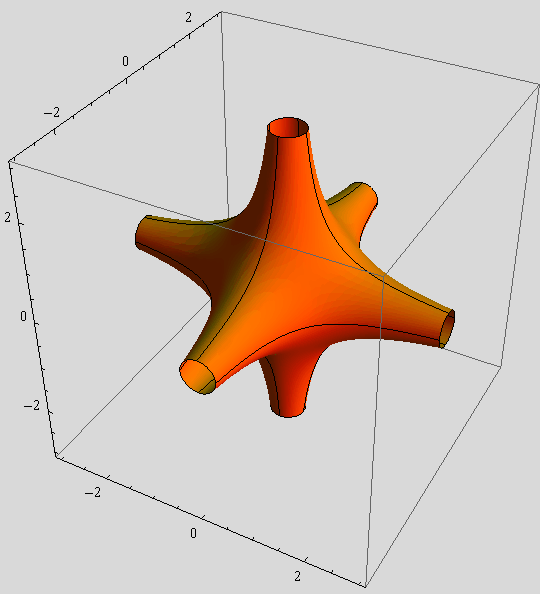
c) S prikaza b) uklonite presjeke s koordinatnim ravninama te pomoću funkcije Specularity osvijetlite plohu s bijelim svjetlom.

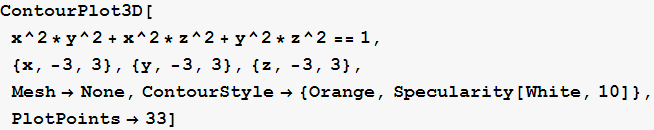
Zadatak za vježbu

Zadatak 1.

Unutar kvadra [-3,3]×[-4,4]×[-4.5,4.5], nacrtajte jednodijelni  i  dvodijelni hiperbolid.
(jednadžbe:    + – = 1  i   – – + = 1)
Neka jedinice na osima budu jednake.

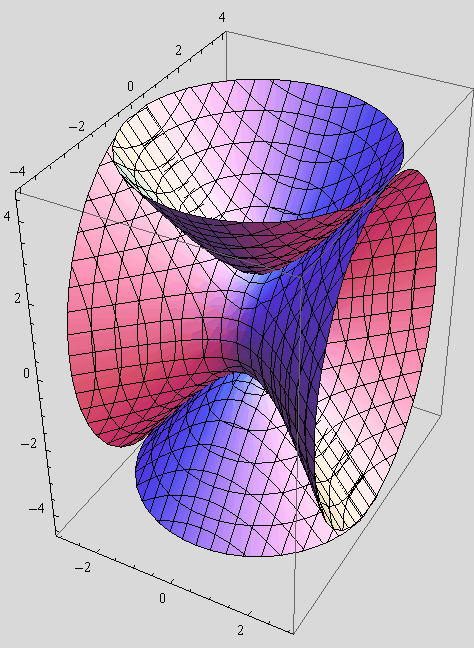
Iste plohe obojite crveno i zeleno, pridružite im 30% prozirnosti te uklonite koordinatne krivulje.
Opciji PlotPoints pridružite vrijednost 20.

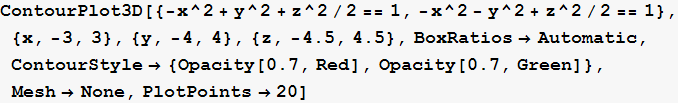
RegionPlot3D

Zadatak 1.

Prikažite dio prostora, unutar kocke ++>1.5.

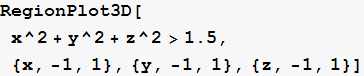
Granice gornjeg trodimenzionalnog područja prikažite s prozirnošću od 30%, obojite ih narandžasto te s njih uklonite linije.

Zadatak 2.

Prikažite trodimenzionalno područje, unutar prizme
+ < 1   i   + > -1.
Granice  područja prikažite s prozirnošću od 30%, obojite ih ljubičasto te s njih uklonite linije.
Upotrijebite opciju PlotPoints→20.

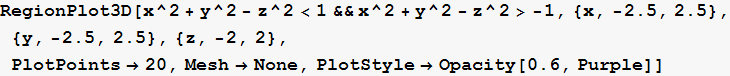
Zadaci za vježbu

Zadatak 1.

Prikažite trodimenzionalno područje, unutar kocke
x^2+y^2<z^2+1.
Uklonite linije s granice područja.

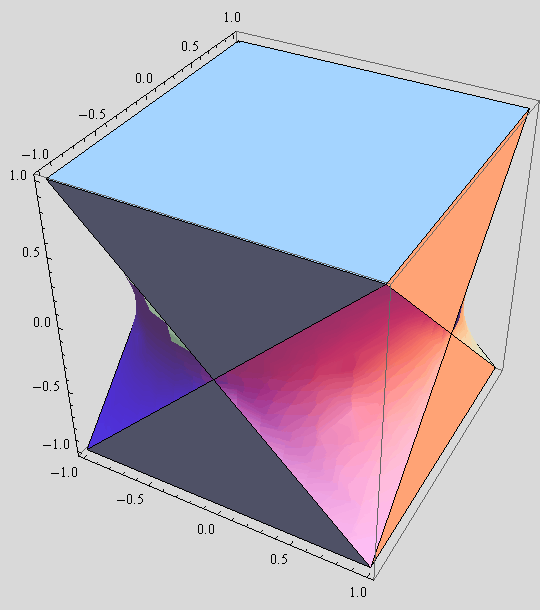
Zadatak 2.

Prikažite trodimenzionalno područje, unutar kocke
.
Granice  područja prikažite s prozirnošću od 30% te s njih uklonite linije.
Upotrijebite opciju PlotPoints→30.

Zadatak 3.

Prikažite trodimenzionalno područje, unutar kocke
+ < 4   i   + < 1.

Notebook izradili: Vladimir Benić i Sonja Gorjanc

Created by Wolfram Mathematica 6.0  (13 April 2008)