Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
7. vježbe

2D grafika

Graphics

Zadatak 1.

Nacrtajte sljedeće prometne znakove

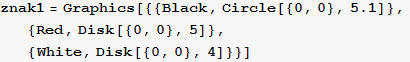
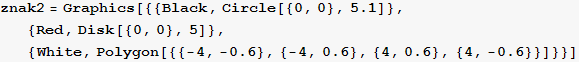
ParametricPlot

Zadatak 1.

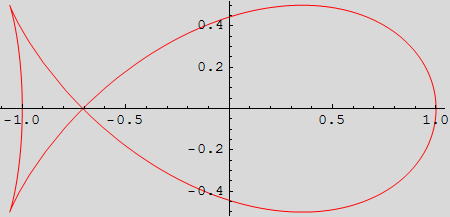
Nacrtajte krivulju zadanu parametarskim jednadžbama:
     x(t) = cost -
      y(t) = sint cost,   t ε [0,2π].
Obojite ju crveno.      

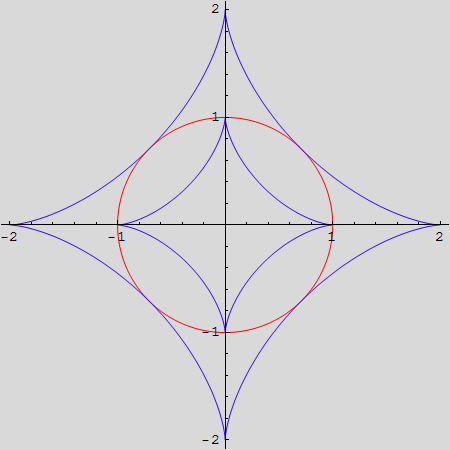
Zadatak 3.

Na istoj slici nacrtajte jediničnu kružnicu i dvije astroide (a=1 i a=2). Kružnicu obojite crvenom, a astroide plavom bojom.
Uputa: Parametarske jednadžbe astroide su
     x(t)=a·t
      y(t)=a·t,   tε[0,2π].

Zadatak 2.

Pomoću funkcije Manipulate napravite animaciju iscrtavanja elipse kojoj su poluosi a=3 i  b=2  parelelne s osi x, odnosno  y,  a koordinate središta (2, -1).
Uputa: Parametarske jednadžbe elipse su
     x(t)=a·cost+p
      y(t)=b·sint+q,   t ε [0,2π].

Zadaci za vježbu

Zadatak 1.

Koristeći naredbu ParametricPlot nacrtajte hiperbolu kojoj su poluosi a=3 i  b=2  parelelne s osi x, odnosno  y,  a koordinate središta (-3, 3).
Neka jedinice na osima budu jednake.
Uputa: Parametarske jednadžbe hiperbole su
     x(t)=a·sect+p
      y(t)=b·tant+q,   t ε [0, 2π].

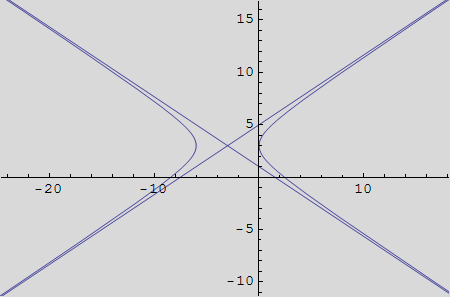
Zadatak 2.

Nacrtajte krivulju kojoj su parametarske jednadžbe
     x(t)=sect
      y(t)=csct,   tε[0,2π].

Pomoću opcije PlotRange nacrtajte ju u području [-5,5]×[-5,5].
Što znači upozorenje koje vam Mathematica ispisuje?

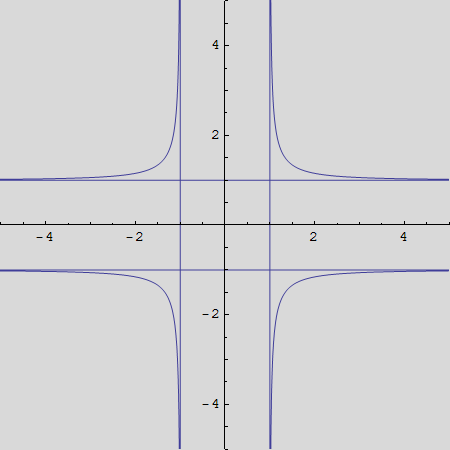
PolarPlot

Zadatak 1.

Polarna  jednadžba krivulje je  r(φ)=cos(e·φ).
Nacrtajte tu krivulju za  φε[0,30 π],  obojite ju crveno na žutoj podlozi i neka Mathematica pri tom ne iscrtava koordinatne osi.

Zadatak 2.

Polarna  jednadžba logaritamske spirale je
r(φ)=.
Na istoj slici nacrtajte 2 logaritamske spirale  (za a= i a=), za φε[0,8π],  i obojite ih crvenom i plavom bojom.

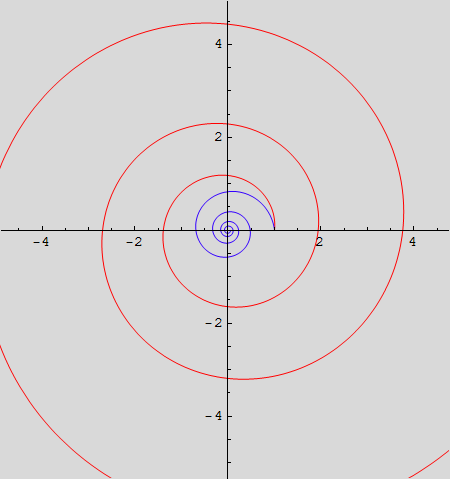
Zadatak 3.

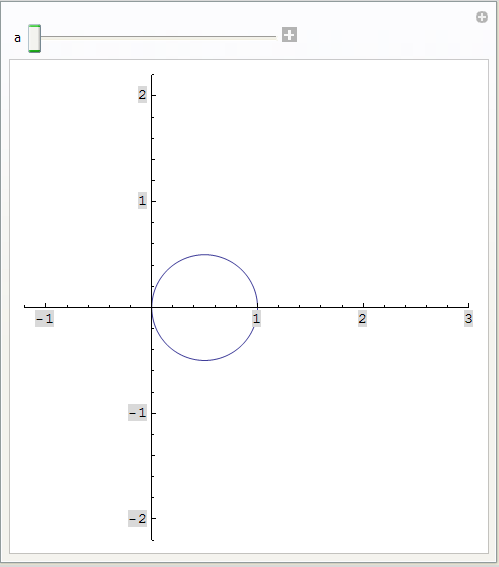
Pomoću funkcije Manipulate pokažite kako se, za interval [0,4π], mijenja oblik krivulje čija je polarna jednadžba
r(φ)= a +cos φ,
ako realni parametar a poprima vrijednosti između 0 i 2.
Neka za svaku od dobivenih krivulja Mathematica prikazuje područje (-1.2,3)×(-2.2,2.2).
(opcija PlotRange)

Zadaci za vježbu

Zadatak 1.

Polarna  jednadžba krivulje je  r(φ)= - 2cos4t + .
Nacrtajte tu krivulju za  tε[0, 9π],  obojite ju plavo na svijetlo plavoj podlozi i neka Mathematica pri tom ne iscrtava koordinatne osi.

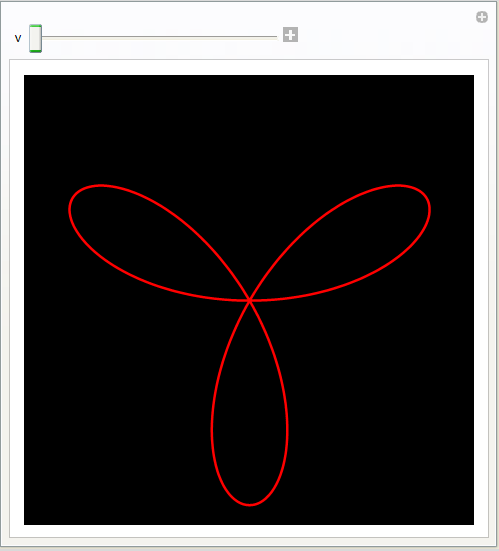
Zadatak 2.

Polarna  jednadžba krivulje je
r(u)=sin 3u, u ∈ [0, π].
Pomoću funkcije Manipulate rotirajte tu krivulju oko ishodišta koordinatnog sustava. Neka je krivulje crvena, a podloga crna.

ContourPlot

Zadatak 1

Krivulja je zadana jednadžbom   =–),  za xε[–1,1].
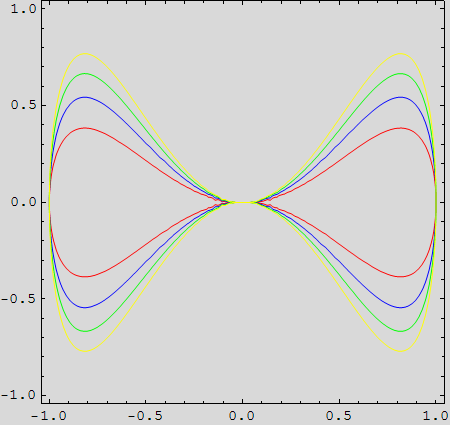
Na istoj slici nacrtajte 4 takve krivulje (za a=1, a=2, a=3 i a=4) i obojite ih redom crvenom, plavom, zelenom
i žutom bojom.

Zadatak 2.

a) Nacrtajte krivulju koja je zadana jednadžbom
–2·y+2=0,  za (x,y) ε.
Upotrijebite opciju PlotPoints da dobijete precizan crtež u okolini singularne točke.
Neka Mathematica ne iscrtava okvir (opcija Frame).

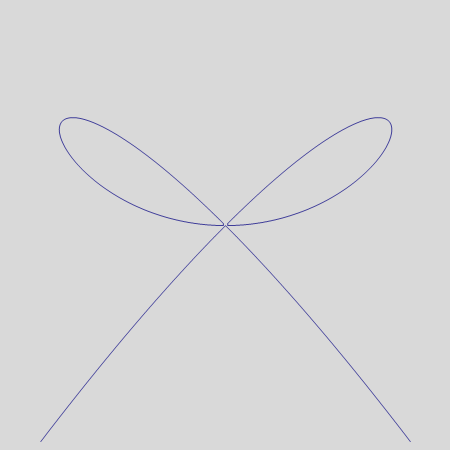
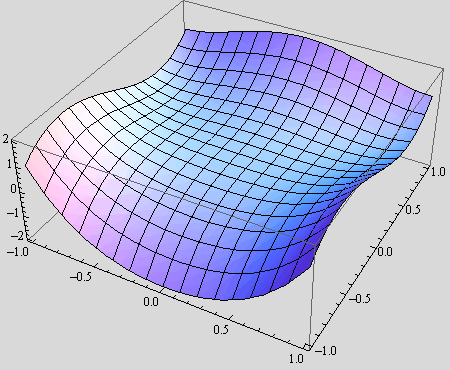
b) Nacrtajte plohu koja je zadana jednadžbom
z=–2·y+2,  za (x,y) ε.

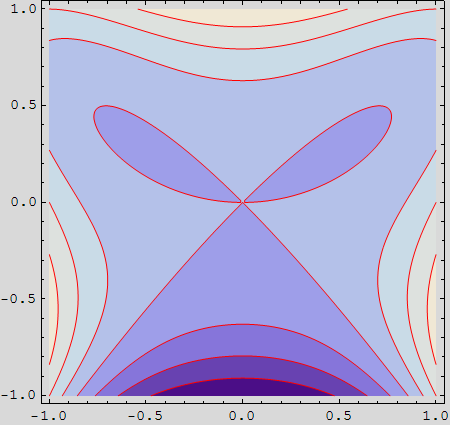
c) Nacrtajte nivo linije gornje plohe. Obojite ih crveno.

Zadatak za vježbu

Zadatak 1.

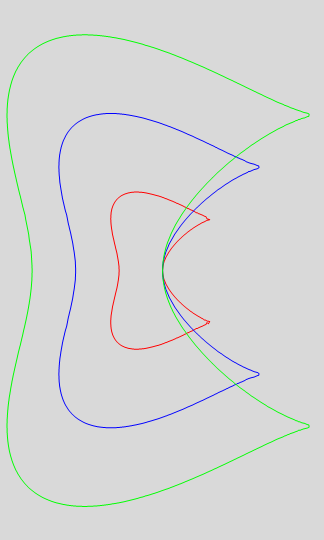
a) Krivulja je zadana jednadžbom  (–)+=0,  za xε[–a,a].
Na istoj slici, u području [-3,3]×[-5,5] nacrtajte 3 takve krivulje (za a=1, a=2 i a=3) i obojite ih crvenom, plavom i zelenom bojom.
Neka su jedinice na osima jednake i neka Mathematica ne iscrtava okvir.

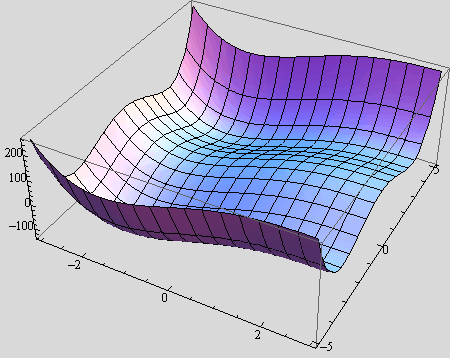
b) Nacrtajte plohu koja je zadana jednadžbom
z=(–)+,  za (x,y) ε [-3,3]×[-5,5].

c) Nacrtajte nivo linije gornje plohe. Obojite ih žuto.

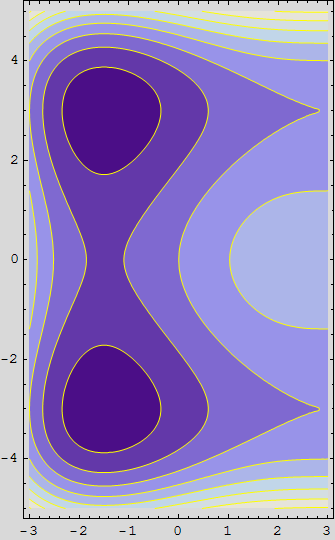
RegionPlot

Zadatak 1

Dio kvadratnog područja u kojem vrijedi  
<   
obojite crveno i obrubite debelom crnom linijom. Preostali dio područja neka bude sive boje. Neka Mathematica ne iscrtava okvir.

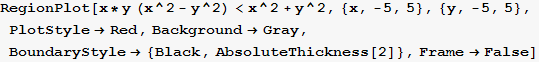
Zadatak 2.

Dio kvadratnog područja u kojem vrijedi  
>   ili   <0.04,
pomoću funkcije ColorFunction obojite s "Rainbow". Neka podloga bude bijela.

Zadatak za vježbu

Zadatak 1.

Dio  područja [–1,1]×[–2,2] u kojem vrijedi  
>   i   | y | < 1.5,
pomoću funkcije ColorFunction obojite s "Rainbow". Neka podloga bude crna.

Show

Zadatak 1.

Hiperbola i kružnica dane su implicitnim jednadžbama
-=1  i   +=9.
Izračunajte koordinate njihovih sjecišta, a zatim nacrtajte obe krivulje i na crtežu njihova sjecišta istaknite crvenom bojom.

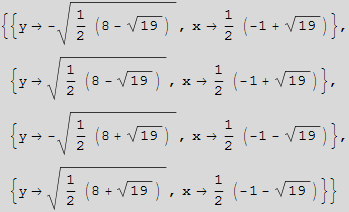
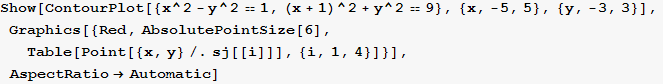
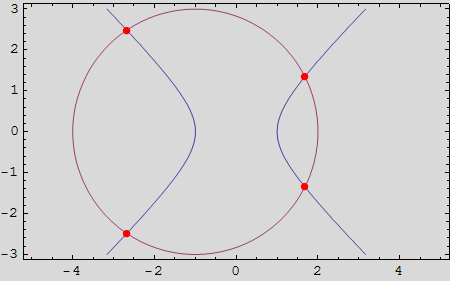
Zadatak 2.

Središte elipse je u ishodištu, a poluosi   a=5 i  b=3  parelelne s osi x, odnosno  y.
Pomiću funkcije Manipulate, napravite animaciju generiranja te elipse kao skupa točaka kojima je zbroj udaljenosti od fokusa konstantan.
Uputa: Animirajte radij-vektore (spojnice fokusa s točkama elipse).
            e= je udaljenost fokusa od sredista elipse

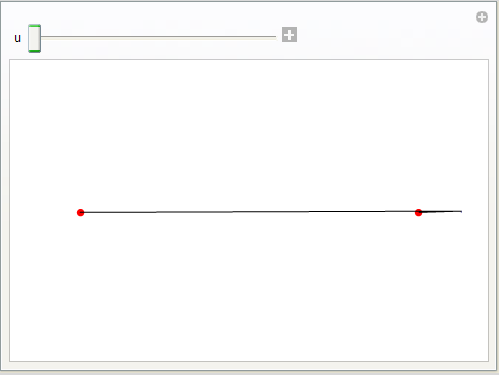
Zadatak za vježbu

Zadatak 1.

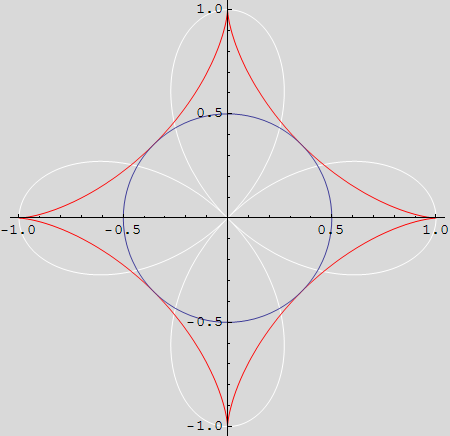
Na istoj slici nacrtajte krivulje , i .
1. Polarna  jednadžba krivulje je:
     r(φ)=cos(2·φ),   φε[0,π].
2. Parametarske jednadžbe  krivulje su:
     x(t)=t
      y(t)=t,   tε[0,2π].
3. Implicitna  jednadžbe  krivulje je:
    +=0.25,  za  xε[–0.5,0.5].

Notebook izradili: Vladimir Benić i Sonja Gorjanc

Created by Wolfram Mathematica 6.0  (05 April 2008)