Provjerite, koristeći derivaciju, dobiveni rezultat.
Uputa: Tražena funkcije se dobije integriranjem zadane funkcije f(x).
Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
6. vježbe
Integrali
Neodređeni integrali
Zadatak 1.
Koju funkciju treba derivirati da se dobije funkcija f(x)=![]() cos(4x)?
cos(4x)?
Provjerite, koristeći derivaciju, dobiveni rezultat.
Uputa: Tražena funkcije se dobije integriranjem zadane funkcije f(x).
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
![]()
Out[2]=
![]()
Zadaci za vježbu
Zadatak 1.
Koju funkciju treba derivirati da se dobije funkcija f(x)=![]() arctg x? Provjerite, koristeći derivaciju, dobiveni rezultat.
arctg x? Provjerite, koristeći derivaciju, dobiveni rezultat.
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
![]()
Zadatak 2.
Izračunajte ![]() i deriviranjem provjerite dobiveni rezultat.
i deriviranjem provjerite dobiveni rezultat.
In[5]:=
![]()
Out[5]=
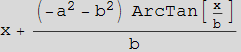
In[6]:=
![]()
Out[6]=
![]()
Određeni integrali
Zadatak 1.
Brzina v matrijalne točke, ovisna o vremenu t, zadana je formulom v(t)=0.3·cos![]() +0.5.
+0.5.
Koliki put prijeđe matrijalna točka od ![]() =0.2 do
=0.2 do ![]() =1?
=1?
Uputa: Put je jedank određenom integralu brzine od ![]() do
do ![]() .
.
In[7]:=
![]()
In[8]:=
![]()
Out[8]=
![]()
Zadatak 2.
Odredite duljinu luka grafa funkcije f(x)=sin2x nad segmentom [0,![]() ]. Rezultat prikažite pomoću 50 znamenki.
]. Rezultat prikažite pomoću 50 znamenki.
Uputa: Duljina luka krivulje y=f(x) nad segmentom [a,b] jednaka je ![]() .
.
In[9]:=
![]()
In[10]:=
![]()
In[11]:=
![]()
Out[11]=
![]()
Zadatak 3.
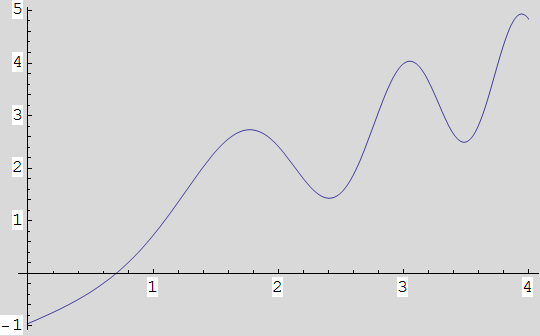
. Definirajte funkciju f(x)=x+sin(![]() +5).
+5).
. Crtanjem grafa funkcije f(x) na segmentu [0, 4] provjerite da je funkcije pozitivna na segmentu [1, 3].
In[12]:=
![]()
In[13]:=
![]()
Out[13]=
. Pomoću opcije Filling->Axis obojite dio ravnine omeđen s osi x, vertikalama x=1 i x=3, te grafom funkcije f. Upotrijebite opciju AxesOrigin->{0,0}, tako da se osi x i y sijeku u ishodištu.
In[14]:=
![]()
Out[14]=
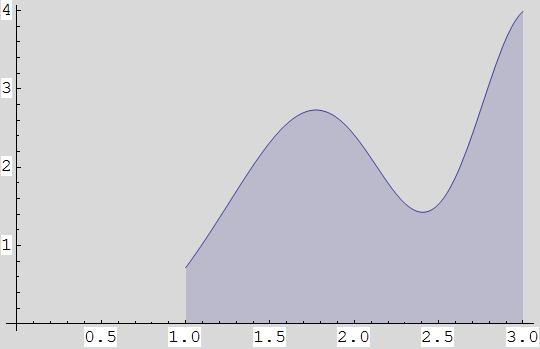
. Izračunajte površinu obojenog dijela, tj. od grafa do osi x nad segmentom [1,3].
Uputa: Ako je funkcija pozitivna na zadanom segmentu onda je površina jednaka određenom integralu funkcije nad tim segmentom.
In[15]:=
![]()
Out[15]=
![]()
Zadatak 4.
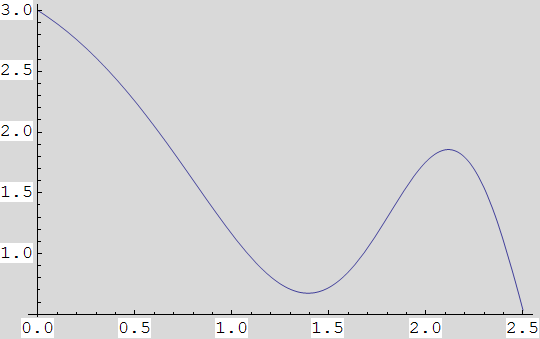
a) Definirajte funkciju h(x)=3-x-sin![]() i nacrtajte njezin graf nad segmentom [0,2.5].
i nacrtajte njezin graf nad segmentom [0,2.5].
In[16]:=
![]()
In[17]:=
![]()
Out[17]=
b) Odredite volumen rotacijskog tijela koje nastaje rotacijom dijela ravnine od grafa funkcije h(x)=3-x-sin![]() do x osi nad segmentom [0,2.5], oko osi y.
do x osi nad segmentom [0,2.5], oko osi y.
Uputa: Rotacijski volumen jednak je ![]() = 2π
= 2π ![]() .
.
In[18]:=
![]()
Out[18]=
![]()
d) Pomoću funkcije RevolutionPlot3D, nacrtajte plohu koja nastaje rotacijom gornjeg grafa oko osi y.
In[19]:=
![]()
Out[19]=
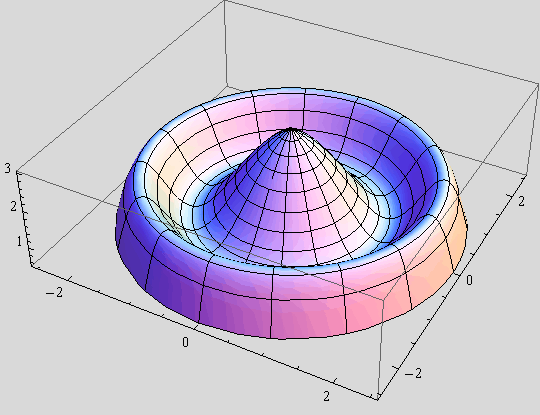
e) Odredite volumen rotacijskog tijela koja nastaje rotacijom dijela ravnine od grafa funkcije h(x)=3-x-sin![]() do x osi nad segmentom [0,2.5], oko osi x.
do x osi nad segmentom [0,2.5], oko osi x.
Uputa: Rotacijski volumen jednak je ![]() = π
= π ![]() .
.
In[20]:=
![]()
Out[20]=
![]()
f) Pomoću funkcije RevolutionPlot3D, nacrtajte plohu koja nastaje rotacijom gornjeg grafa oko osi x.
In[21]:=
![]()
Out[21]=

Zadaci za vježbu
Zadatak 1.
Sila f, ovisna o x, zadana formulom f(x) = 0.4·sin(2x+1)+9.81, vrši rad po x osi od ![]() =0.1 do
=0.1 do ![]() =0.8. Koliki je taj rad?
=0.8. Koliki je taj rad?
Uputa: Rad je jednak određenom integralu sile od ![]() do
do ![]() .
.
In[22]:=
![]()
Out[22]=
![]()
Zadatak 2.
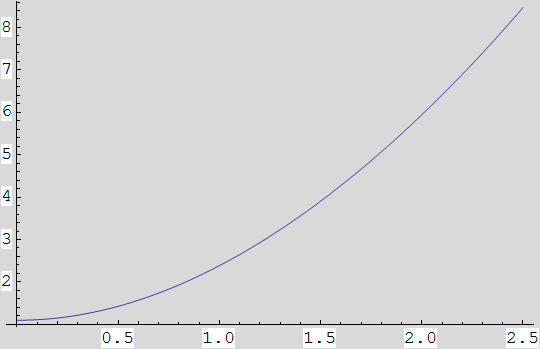
Crtanjem grafa funkcije g(x)=![]() +ln(
+ln(![]() +3) na segmentu [0, 2.5] provjerite da je funkcije pozitivna na segmentu [1, 2].
+3) na segmentu [0, 2.5] provjerite da je funkcije pozitivna na segmentu [1, 2].
In[23]:=
![]()
In[24]:=
![]()
Out[24]=
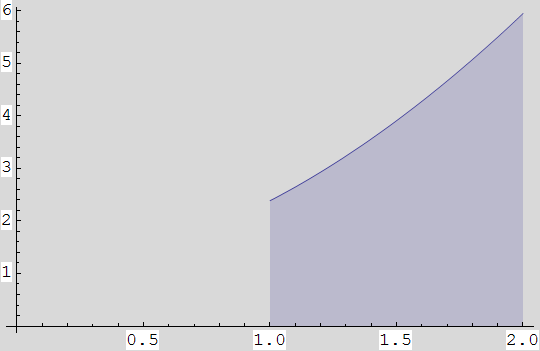
Obojite dio ravnine omeđen s osi x, vertikalama x=1 i x=2, te grafom funkcije g.
In[25]:=
![]()
Out[25]=
Odredite površinu od grafa do x osi nad segmentom [1, 2] (točnu i približnu vrijednost).
In[26]:=
![]()
Out[26]=
![]()
In[27]:=
![]()
Out[27]=
![]()
Zadatak 3.
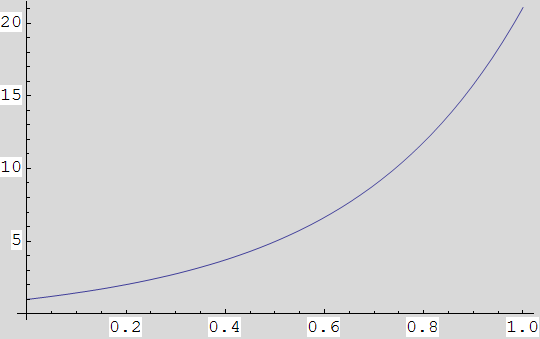
a) Nacrtajte graf funkcije f(x)=x+![]() nad segmentom [0,1].
nad segmentom [0,1].
In[28]:=
![]()
Out[28]=
b) Odredite volumen rotacijskog tijela koje nastaje rotacijom dijela ravnine od grafa funkcije f(x)=x+![]() do x osi nad segmentom [0,1], oko osi y.
do x osi nad segmentom [0,1], oko osi y.
c) Rezultat prikažite pomoću 30 znamenki.
Uputa: Rotacijski volumen jednak je ![]() = 2π
= 2π ![]() .
.
In[29]:=
![]()
Out[29]=
![]()
In[30]:=
![]()
Out[30]=
![]()
d) Pomoću funkcije RevolutionPlot3D, nacrtajte plohu koja nastaje rotacijom gornjeg grafa oko osi y.
In[31]:=
![]()
Out[31]=
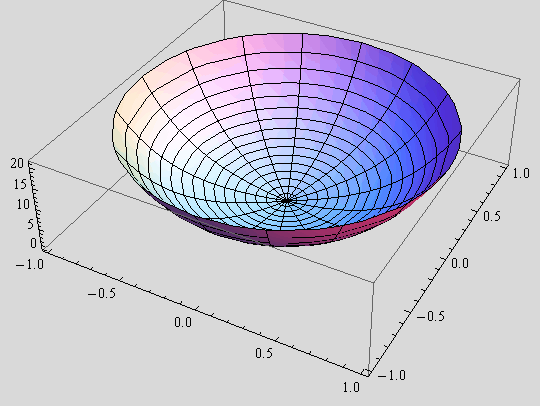
e) Odredite volumen rotacijskog tijela koja nastaje rotacijom dijela ravnine od grafa funkcije f(x)=x+![]() do x osi nad segmentom [0,1], oko osi x.
do x osi nad segmentom [0,1], oko osi x.
Uputa: Rotacijski volumen jednak je ![]() = π
= π ![]() .
.
In[32]:=
![]()
Out[32]=
![]()
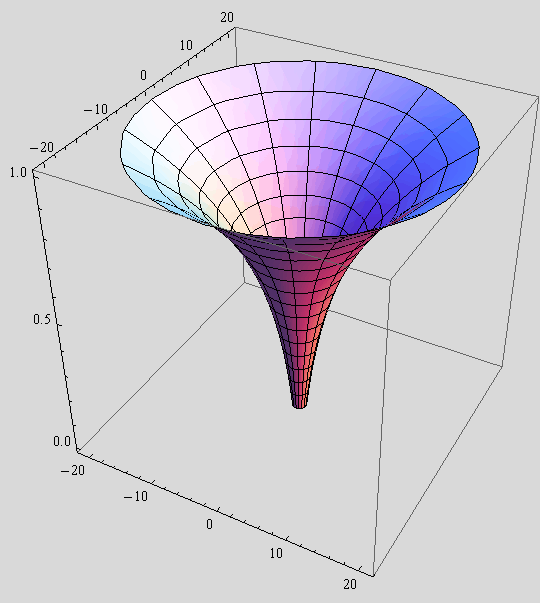
f) Pomoću funkcije RevolutionPlot3D, nacrtajte plohu koja nastaje rotacijom gornjeg grafa oko osi x.
In[33]:=
![]()
Out[33]=
Diferencijalne jednadžbe
Naredba DSolve
Zadatak 1.
Pomoću naredbe DSolve riješite sljedeće diferencijalne jednadžbe:
xy'=2y-x
In[34]:=
![]()
Out[34]=
![]()
y'cosx+ysinx-1=0 za početni uvjet y(0)=2
In[35]:=
![]()
Out[35]=
![]()
y''-y=![]()
In[36]:=
![]()
Out[36]=
![]()
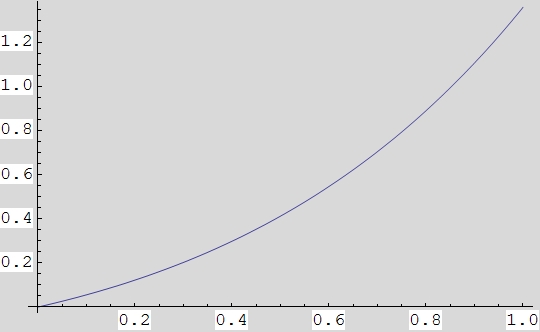
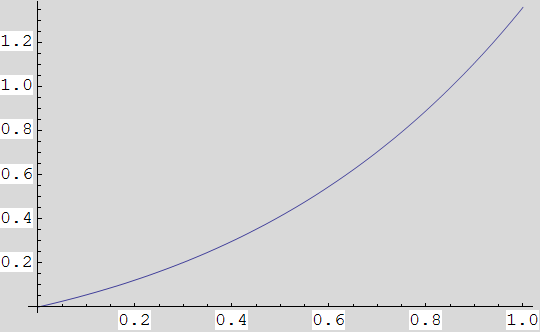
y''-y=![]() za početne uvjete y'(1)=e, y(0)=0.
za početne uvjete y'(1)=e, y(0)=0.
In[37]:=
![]()
Out[37]=
![]()
Funkciju koja je rješenje možemo dobiti ovako (pogodno za partikularna rješenje)
In[38]:=
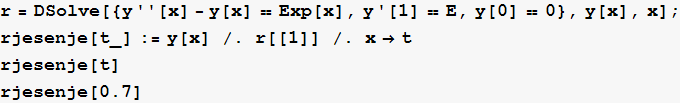
Out[40]=
![]()
Out[41]=
![]()
In[42]:=
![]()
Out[42]=
Drugi način, pomoću "čiste funkcije".
In[43]:=
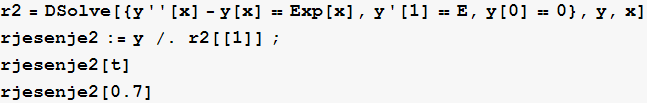
Out[43]=
![]()
Out[45]=
![]()
Out[46]=
![]()
In[47]:=
![]()
Out[47]=
(x+y)dx+(x+2y)dy=0
In[48]:=
![]()
Out[48]=
![]()
Zadaci za vježbu
Zadatak 1.
Riješite sljedeće diferencijalne jednadžbe:
xy'=2x-x za početni uvjet y(1)=2
In[49]:=
![]()
Out[49]=
![]()
y''+y=sinx
In[50]:=
![]()
Out[50]=
![]()
dy+y=2![]() dx za početni uvjet y(0)=3.
dx za početni uvjet y(0)=3.
In[51]:=
![]()
Out[51]=
![]()
Notebook izradili: Vladimir Benić i Sonja Gorjanc