Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
5. vježbe
Limesi i derivacije
Limesi nizova i funkcija
Zadatak 1.
Izračunajte ![]()
In[1]:=
![]()
Out[1]=
![]()
Zadatak 2.
Zadana je funkcija f(x)= ![]() .
.
Funkcija, očigledno, nije definirana za x=0. Odredite njezin limes s lijeva i s desna kada x→0.
In[2]:=
![]()
Out[2]=
![]()
Out[3]=
![]()
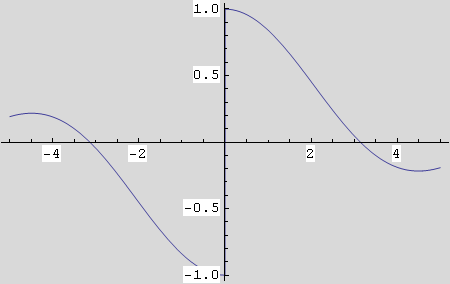
Rezultat: limesi s lijeva i s desna su različiti. Limes s lijeva iznosi -1, a s desna 1.
Nacrtajte graf funkcije f nad segmentom [-5,5].
In[4]:=
![]()
Out[4]=
Zadaci za vježbu
Zadatak 1.
Izračunajte ![]()
In[5]:=
![]()
Out[5]=
![]()
Izračunajte ![]() lnx·ln(x-1)
lnx·ln(x-1)
In[6]:=
![]()
Out[6]=
![]()
Izračunajte ![]() x·sin
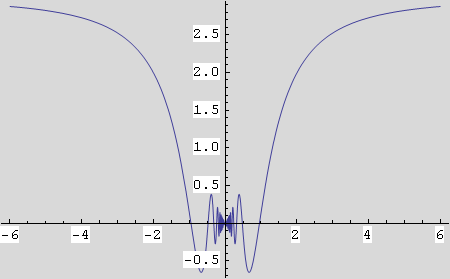
x·sin![]() i nacrtajte graf dunkcije x·sin
i nacrtajte graf dunkcije x·sin![]() nad segmentom [-6,6].
nad segmentom [-6,6].
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
Out[8]=
Zadatak 2.
- Definirajte funkciju f(x)=![]() .
.
- Odredite vertikalne asimptote te funkcije.
- Pokažite da graf funkcije ima jednu kosu asimptotu i odredite njezinu jednadžbu.
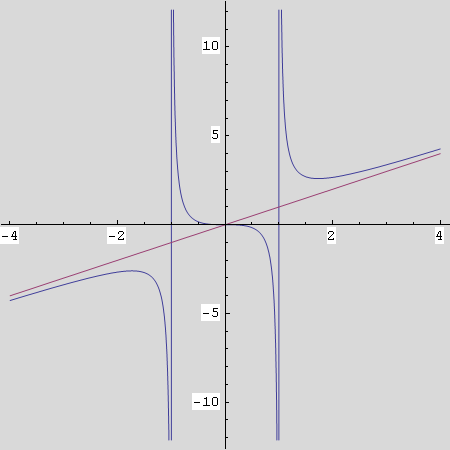
- Nacrtajte graf funkcije f i njegove asimptote nad segmentom [-4,4].
Neka je okvir slike kvadratni.
- Uklonite vrijednost funkcije f.
Uputa: Pravac y=kx+l je kosa asimptota ako je k=![]()
![]() i l=
i l=![]() ( f(x)-k·x).
( f(x)-k·x).
In[9]:=
![]()
In[10]:=
![]()
Out[10]=
![]()
In[11]:=
![]()
Out[11]=
![]()
In[12]:=
![]()
Out[12]=
![]()
In[13]:=
![]()
Out[13]=
![]()
Verikalne asimptote su x=±1.
In[14]:=
![]()
Out[14]=
![]()
Out[15]=
![]()
In[16]:=
![]()
Out[16]=
![]()
Out[17]=
![]()
Kosa asimptota je y=x.
In[18]:=
![]()
Out[18]=
In[19]:=
![]()
Zadatak 3.
- Definirajte funkciju f(x)=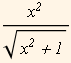 .
.
- Odredite njezine kose asimptote, posebno za x→+∞ , a posebno za x→ –∞.
- Provjerite da se dobiju dvije različite asimpote.
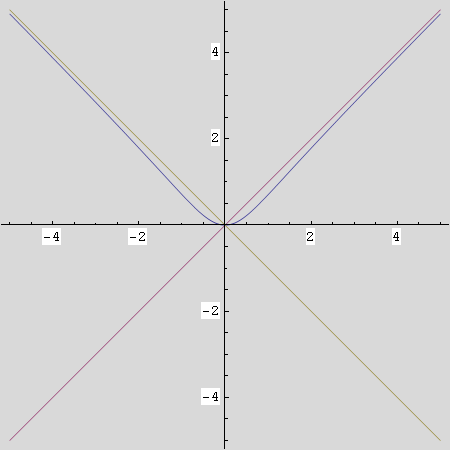
- Nacrtajte graf funkcije f i njegove asimptote nad segmentom [-4,4].
Neka jedinice na osima budu jednake.
- Uklonite vrijednost funkcije f.
Uputa: Pravac y=kx+l je kosa asimptota ako je k=![]()
![]() i l=
i l=![]() ( f(x)-k·x).
( f(x)-k·x).
In[20]:=
![]()
In[21]:=
![]()
Out[21]=
![]()
Out[22]=
![]()
Desna kosa asimptota, za x→+∞ , je y=x.
In[23]:=
![]()
Out[23]=
![]()
Out[24]=
![]()
Lijeva kosa asimptota, za x→ –∞, je y=–x.
In[25]:=
![]()
Out[25]=
In[26]:=
![]()
Derivacije funkcija jedne varijable
Zadatak 1
Za funkciju g(x)=![]() izračunajte:
izračunajte:
- prvu, drugu i treću derivaciju,
- numeričku vrijednost njezine pete derivacije u x=6.
In[27]:=
![]()
In[28]:=
![]()
Out[28]=
![]()
In[29]:=
![]()
Out[29]=
![]()
In[30]:=
![]()
Out[30]=
![]()
In[31]:=
![]()
Out[31]=
![]()
In[32]:=
![]()
Zadatak 2.
Pomoću funkcije Manipulate prikažite prvih 15 derivacija funkcije h(x)=lnx.
In[33]:=
![]()
In[34]:=
![]()
Out[34]=
In[35]:=
![]()
Zadatak 3.
Odredite ekstreme funkcije
f(x)= 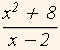
1. korak:
- Definirajte gornju funkciju.
- Izračunajte prvu derivaciju te funkcije.
- Pomoću NSolve odredite nultočke dobivene derivacije.
Dobit ćete x koordinate stacionarnih točaka.
In[36]:=
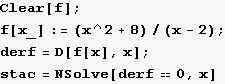
Out[39]=
![]()
![]()
2. korak:
- Izračunajte vrijednost druge derivacije funkcije f za stacionarne točke.
- Zaključite za koji x funkcija f ima minimum, a za koji maksimum.
In[40]:=
![]()
Out[40]=
![]()
![]()
3. korak:
- Odredite y koordinate ekstrema, te konačno točke ekstrema.
In[41]:=
![]()
Out[41]=
![]()
Zaključak:
u točki (5.4641; 10.9282) funkcija ima minimum,
a u točki (-1.4641; -2.9282) funkcija ima maksimum.
Za provjeru, nacrtajte graf funkcije za x∈[–10;10].
In[42]:=
![]()
Out[42]=
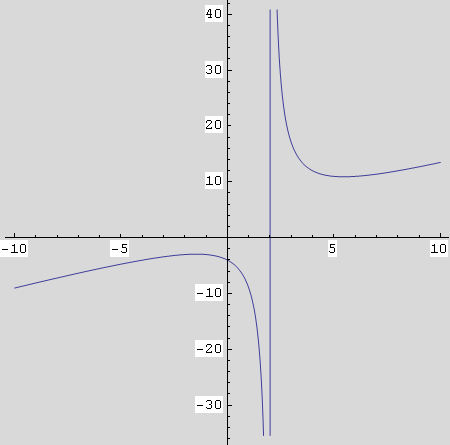
Zadaci za vježbu
Zadatak 1
Za funkciju g(x)=![]() izračunajte:
izračunajte:
- prvu i drugu derivaciju te pojednostavnite dobivene izraze pomoću naredbe Simplify,
- numeričku vrijednost pete derivacije u x=7.
In[43]:=
![]()
Out[43]=
![]()
In[44]:=
![]()
Out[44]=
![]()
In[45]:=
![]()
Out[45]=
![]()
In[46]:=
![]()
Out[46]=
![]()
In[47]:=
![]()
Out[47]=
![]()
Zadatak 2.
Odredite ekstreme funkcije f(x)= ![]() i nacrtajte graf s istaknutim minimumom i maksimumom.
i nacrtajte graf s istaknutim minimumom i maksimumom.
In[48]:=
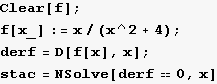
Out[51]=
![]()
In[52]:=
![]()
Out[52]=
![]()
In[53]:=
![]()
Out[53]=
![]()
In[54]:=
![]()
Out[54]=
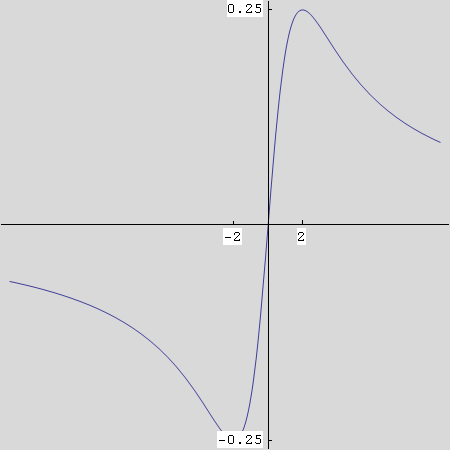
In[55]:=
![]()
Out[55]=
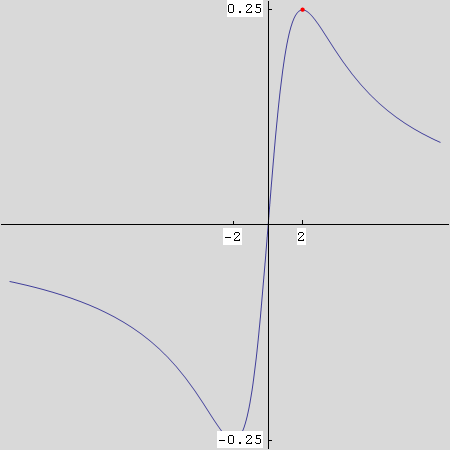
Zadatak 3.
Matrijalna točka giba se tako da joj brzina v ovisi o vremenu t po formuli: v(t)=0.1·sin(2t+1)+0.5.
Nalaženjem ekstrema odredite trenutak ![]() ∈(0,1) u kojem matrijalna točka počinje usporavati.
∈(0,1) u kojem matrijalna točka počinje usporavati.
Uputa: Ako za t = ![]() matrijalna točka počinje usporavati to znači da lijevo od
matrijalna točka počinje usporavati to znači da lijevo od ![]() brzina raste, a desno pada, tj. brzina u
brzina raste, a desno pada, tj. brzina u ![]() ima maksimum. Zadatak se svodi na nalaženje maksimuma funkcije v(t) u intervalu (0; 1).
ima maksimum. Zadatak se svodi na nalaženje maksimuma funkcije v(t) u intervalu (0; 1).
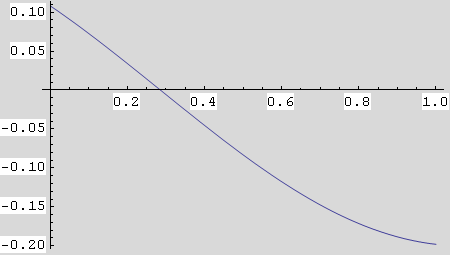
1. Definirajmo funkciju v(t), odredimo prvu derivaciju v'(t) i nađimo njenu nultočku pomoću funkcije FindRoot.
Aproksimativnu nultočku, koja nam treba za primjenu funkcije FindRoot, naći ćemo crtanjem grafa derivacije.
In[56]:=
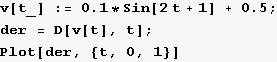
Out[58]=
In[59]:=
![]()
Out[59]=
![]()
2. Ispitajmo prirodu ekstrema pomoću druge derivacije
In[60]:=
![]()
Out[60]=
![]()
Druga derivacija je negativna pa v(t) ima maksimum.
3. Traženi trenutak t je:
In[61]:=
![]()
Out[61]=
![]()
Derivacije funkcija više varijabli
Zadatak 1
Za funkciju f(x,y)= ![]() izračunajte:
izračunajte:
- ![]() i
i ![]() ,
,
- ![]() .
.![]() u točki (0,-3).
u točki (0,-3).
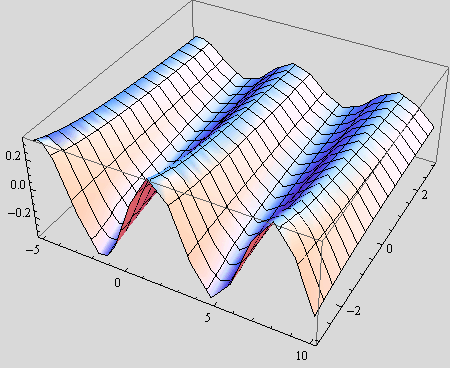
Nacrtajte graf funkcije f nad područjem (-5,10)×(-3,3)
In[62]:=
![]()
In[63]:=
![]()
In[64]:=
![]()
Out[64]=
![]()
In[65]:=
![]()
Out[65]=
![]()
In[66]:=
![]()
Out[66]=
![]()
In[67]:=
![]()
Out[67]=
Zadatak za vježbu
Zadatak 1
Za funkciju f(x,y)= sin (x·y) izračunajte prve i druge parcijalne derivacije i nacrtajte graf nad područjem (-π,π) ×(![]() ,
,![]() ).
).
In[68]:=
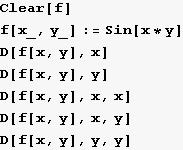
Out[70]=
![]()
Out[71]=
![]()
Out[72]=
![]()
Out[73]=
![]()
Out[74]=
![]()
In[75]:=
![]()
Out[75]=
Notebook izradili: Vladimir Benić i Sonja Gorjanc