Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
4. vježbe

Jednadžbe, sustavi jednadžbi i nejednadžbe

Polinomijalne jednadžbe stupnja manjeg od 5 -- Solve

Zadatak 1

Izračunajte točna rješenja jednadžbe -18+8x+48=0 i izdvojite pravila supstitucije za 2. i 3. rješenje.

Zadatak 2

Spremite polinom   -   - 6  u varijablu pol, riješite jednadžbu pol=0 i rješenja nazovite rj.

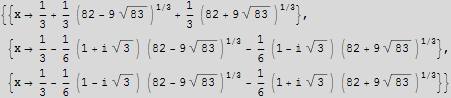
Izdvojite  numeričku vrijednost 2. rješenja.

Ispišite numeričku vrijednost 3. rješenja (ne kao pravilo supstitucije).

Spremite numeričku vrijednost trećeg rješenja u varijablu x3 i provjerite, uvrštavanjem x3 u pol, da je x3 nultočka.

Točnim računom trebali biste, kao rezultat, dobiti 0. No, zbog približnog računa rezultat se razlikuje od nule što je normalno.
Funkcija Chop rezultate približno jednake nuli zamjenjuje nulama. Proslijedite rezultat supstitucije funkciji Chop.

Zadatak za vježbu

Zadatak

Spremite polinom  -13 -  12+39x-18  u varijablu poli, riješite jednadžbu poli=0 i rješenja nazovite rj.
Izdvojite  numeričku vrijednost 3. rješenja.
Ispišite numeričku vrijednost 4. rješenja (ne kao pravilo supstitucije).
Spremite numeričku vrijednost 4. rješenja u varijablu x4 i provjerite, uvrštavanjem x4 u poli, da je x4 nultočka.

Točnim računom trebali biste, kao rezultat, dobiti 0. No, zbog približnog računa rezultat se razlikuje od nule što je normalno. Funkcija Chop rezultate približno jednake nuli zamjenjuje nulama.
Proslijedite rezultat supstitucije funkciji Chop.

Polinomijalne jednadžbe stupnja većeg od 4 -- NSolve

Zadatak

Riješite jednadžbu 2 - + - 3x - 5=0. Provjerite da je prvi dobiveni rezultat nultočka zadanog polinoma (koristite funkciju Chop).

Zadatak za vježbu

Zadatak

Riješite jednadžbu 2+2 - + + 3x - 5=0.
Provjerite da je prvi dobiveni rezultat nultočka zadanog polinoma.

Proizvoljne jednadžbe -- FindRoot

Zadatak

Odredite negativnu nultočku funkcije f(x) = sin(x) - .

Za određivanje aproksimativnog rješenja počnite s grafom na segmentu [-5; 5].

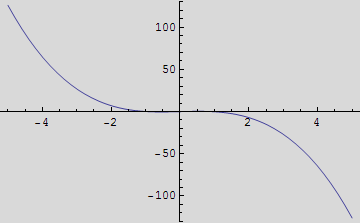
Za točnije određivanje startnog "rješenja" nacrtajte graf na segmentu [-1; -0.5]

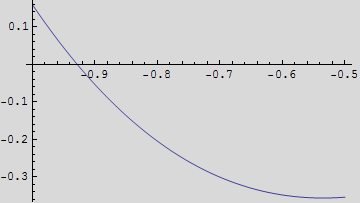
Kao apriksimaciju  odaberite točku -0.9 i primjenite funkciju FindRoot.
Provjerite da je dobiveni broj zaista rješenje.

Zadatak za vježbu

Zadatak

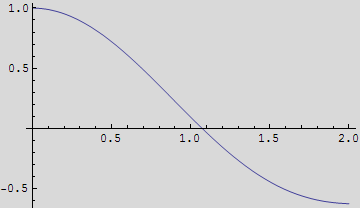
Odredite pozitivnu nultočku funkcije f(x) = x - .
Za određivanje aproksimativnog rješenja počnite s grafom na segmentu [-5; 5].

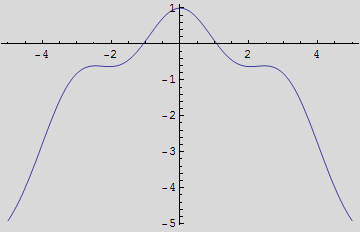
Sustavi jednadžbi

Zadatak 1

Odredite rješenje sustava
2x + y + z = 4
x + 2y + z = 3
x + y + 2z = 2

Sustav ima jedinstveno rješenje

Zadatak 2

Odredite rješenje sustava koji je se od prethodnog razlikuje samo po koeficijentima uz x i y u trećoj jednadžbi
(ti su koeficijenti ovdje jednaki 3).
2x + y + z = 4
x + 2y + z = 3
3x + 3y + 2z = 2

Sustav nema rješenja.

Zadatak 3

Odredite rješenje sustava koji je sličan predhodnom, samo neka  desna strana 3. jednadžbe bude jednaka 7.
2x + y + z = 4
x + 2y + z = 3
3x + 3y + 2z = 7

Sustav ima beskonačno mnogo rješenja, pri čemu je kao parametar izabrana varijabla z.
Drugim riječima, varijabla z može biti bilo koji realan broj dok se odgovarajuće vrijednosti od x i y računaju po gornjim formulma.

Napomena: gornja primjedba programa Mathematica, prikazana crvenim slovima, posljedica je činjenice da Mathematica ne može dati formulu za vrijednost varijable z budući da je z proizvoljan.

Zadatak 4

Odredite koordinate sjecišta pravca y=2x+1 s jediničnom kružnicom.

Zadaci za vježbu

Zadatak 1

Odredite rješenje sustava (točno i približno).
3x + y + 2z = 4
x + 2y + 3z = 7
4x + y + 5 z= 4

Zadatak 2

Pokažite da sljedeći sustav jednadžbi nema rješenja.
Provjerite da je determinanta sustava jednaka 0.
3x + y + 2z = 10
x + 2y + 3z = 3
4x + 3y + 5z = 5

Zadatak 3

Pokažite da sljedeći sustav jednadžbi ima beskonačno mnogo rješenja i odredite njihov parametarski oblik.
3x + y + 2z = 2
x + 2y + 3z = 2
4x + 3y + 5z = 2

Zadatak 4

Odredite koordinate sjecišta pravca y=2x+2 i  kružnice polumjera 2 kojoj je središte u točki (1,0) .

Nejednadžbe

Zadatak 1

Odredite na kojem skupu je - 1  veće od - 1.

Zadatak 2

Odredite domenu funkcije y=ln

Uputa: funkcija ln je definirana za pozitivne brojeve.

Zadaci za vježbu

Zadatak 1

Odredite skup rješenja nejednadžbe  - 3-x+3 ≥ 0.
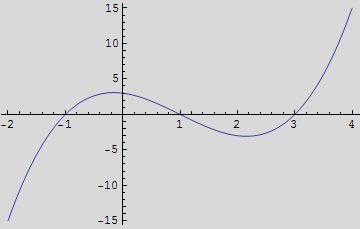
Nacrtajte graf gunkcije f(x)=- 3-x+3 i provjerite dobiveno rješenje.

Zadatak 2

Odredite domenu funkcije y=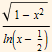

Notebook izradili: Vladimir Benić i Sonja Gorjanc

Created by Wolfram Mathematica 6.0  (18 March 2008)