Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
2. vježbe

Liste, vektori i matrice

Vektorski račun

1. zadatak

Definirajte u Mathematici vektore
= 2. + 3. +   
  = - + 5. +4.
a zatim izračunajte:
1.  2 + ;
2.   - 2;
3.  skalarni umnožak  ·;
4. vektorski  umnožak  ×.

2. zadatak

   
Za vektore   i , definirane u 1. zadatku, izračunajte:
1. modul vektora  
2. kut (u stupnjevima) izmedju i .
3. Otklonite vrijednosti pridružene varijablama a i b.

   
Podsjetnik:
  • Modul vektora se može računati po formuli  || =.
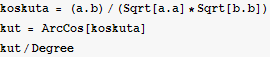
  • Kosinus kuta između vektora i   računamo po formul  .
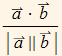  • Ako znamo kosinus nekog kuta, tada ćemo kut dobiti primjenom funkcije ArcCos.
• Množenje kuta u stupnjevim s konstantom Degree pretvara kut u radijane, a dijeljenje kuta u radijanima s Degree pretvara kut u stupnjeve.

Zadaci za vježbu

Definirajte u Mathematici vektore u prostoru
= + 3 + 2.1  
  = - + 5
a zatim izračunajte:
                                       
1.  vektor = 3 -4;
rješenje: =7 -12.2 + 6.3

2.  module vektora i ;
rješenje: || =3.79605,  || =5.39351

3.  skalarni umnožak  ·;
rješenje:   14.9

4.  kut između vektora i , rezultat izrazite u stupnjevima;
rješenje:  106.249°

5.  vektorski  umnožak  ×;
rješenje: ×=-11.13 -2.1 + 8.3

6.  površinu paralelograma što ga određuju vektori    i .
rješenje: 14.042
Uputa: Formula za površinu paralelograma određenog vektorima i je  |×|,  tj. ta je površina jednaka modulu vektorskog umnoška.

Matrični račun

1. zadatak

Napišite matrice

a =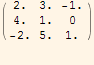
b=.

  Pomoću MatrixForm prikažite ih u standardnom matričnom obliku, a zatim
  1.  izračunajte  3a -2b
  2. izračunajte  a·b
  3. izračunajte inverznu matricu one matrice kojoj je determinanta različita od nule.
      Rezultat prikažite u matričnom obliku.
  4. Otklonite vrijednosti pridružene varijablama a i b.

2. zadatak

Koristeći matrice, odredite rješenje sustava linearnih jednadžbi
   2*x - y +3z = 9
   3*x +y -  z  = 2
    x   +2*y-z = 2

Uputa: Ako je sustav zapisan matrično  Ax=b i ako je det(A)≠0 onda je x=

Zadaci za vježbu

Zadatak 1

Definirajte u Mathematici matrice a i b

a =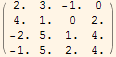

b=,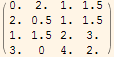

a zatim izračunajte:

1. matricu a.b i prikažite ju u matričnoj formi;    
rješenje:

2. determinantu matrice a;    
rješenje: 84

3. inverznu matricu matrice a;
  rješenje:

4. transponiranu matricu matrice b.
  rješenje:

Zadatak 2

Koristeći matrice, odredite rješenje sustava linearnih jednadžbi

      x         +2 z  = 4
   2 x  +   y +2 z  = 2
–2 x  +2 y  –   z  = 5

rješenje: x=

Uputa: Ako je sustav zapisan matrično, u obliku  Ax=b i ako je det(A)≠0, onda je x=

Dodatak

Liste I

Varijablama a i b pridružite tročlane liste brojeva.
Neka Mathematica pri tome ne ispisuje output.

1. Izračunajte njihov zbroj, razliku, produkt i kvocijent.

2. Izračunajte n-tu potenciju liste a i potencirajte listu a listom b;

3. Izračunajte listu približnih vrijednosti koje funkcija cos poprima na elementima liste a;

4. Otklonite vrijednosti pridružene varijablama a i b i provjerite da ste to učinili.

Zadatak za vježbu

1. Ako su a i b tročlane liste brojeva 3,5.4 i 7, odnosno 1,-3.2 i 0, izračunajte   3-5.
rješenje: {4,163.854,3}

Liste I - naredbe Table i TableForm

1. Pomoću naredbe Table ispišite tablicu svih parnih prirodnih brojeva manjih od 87.

2. Ispišite listu vrijednosti funkcije cos na brojevima 0-π, s korakom .

3. Ispišite gornji rezultat u obliku tablice.

4. Formirajte tablicu parova (x, cos(x)-x) za 0≤x≤π/2 s korakom 0.1.
Rezultat prikažite pomoću funkcije TableForm.
Iz tablice očitajte u kojemo podintervalu funkcija cos(x)-x mijenja predzak tj. u
kojem podintervalu se nalazi njezina nultočka (ili drukčije rečeno: gdje je rješenje jednadžbe cos(x)=x).

Zadatak za vježbu

1. Pomoću naredbe Table formirajte tablicu vrijednosti   kada i ide od 3 do 14 s korakom 2.         rješenje: {9,25,49,81,121,169}

Liste II

1. Varijabli a pridružite dvodimenzionalnu listu 3×2.
2. Prikažite a u obliku tablice.
3. Pomnožite a s listom {1,2,3}.
4. Otklonite vrijednost pridruženu varijabli a.

Liste II - naredbe Table i TableForm

1. Pomoću naredbe Table napravite tablicu množenja za prvih 5 prirodnih brojeva.

2. Formirajte dvodimenzionalna tablicu čiji su elementi , ako i=1,2,3,  a  j=1,2,3,4. Koristite TableForm

Zadatak za vježbu

1. Formirajte dvodimenzionalna tablicu čiji su elementi ako  i=1,2,3,  a  j=1,2,3,4. Koristite naredbu TableForm        
rješenje:   

1

Notebook izradili: Vladimir Benić i Sonja Gorjanc

Created by Wolfram Mathematica 6.0  (25 February 2008)