Programiranje
6. predavanje
"Rupe" u skupu realnih brojeva
Zadatak
Koristeći petlju While napišite program koji će odrediti najveći realni broj pribrojnik koji se dodaje nekom broju br tako da se dobije ponovno br.
Postupak: na početku je pribrojnik jedank broju br i dijelimo pribrojnik sa 2 sve dok se zbroj broja br i pribrojnika pribrojnik razlikuje od br.
Izrada
Testiranje
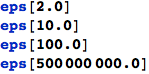
Konstante programa Mathematica vezane uz "rupe" u skupu realnih brojeva
| $MachineEpsilon gives the difference between 1.0 and the next-nearest number representable as a machine-precision number. |
Simulacija ponašanja nekog sustava (diskretno vrijeme)
Osnovna ideja:
1.) početo stanje promatranog sustava prikazuje se podacima u računalu,
2.) vrijeme se mijenja i prelazi se na novi trenutak vremena,
3.) na temelju poznatih pravila, staro stanje sustava se transformira u novo stanje,
4.) koraci 2.) i 3.) se ponavljaju dok ne bude ispunjen neki uvjeta za prestanak simulacije.
Primjer simulacije ponašanja, "gibanje mrava"
Zadatak
Mrav se giba, na slučajan način u kvadratu [0, 50]×[0, 50]. Gibanje počinje iz neke zadane točke i može se gibati na istok, sjever, zapad, jug ili može ostati na mjestu. Svaki izvedeni korak je duljine 1 i svaka od navedenih mogućnosti je jednako vjerojatna. Nacrtajte putanju gibanja mrava postije 2000 vremenskih intervala.
Pložaj mrava određen je koordinatama točke u kojoj se nalazi.
Slučajnost ćemo simulirati tako da će računalo generirati realan slučajan broj r između 0 i 1. Ako r padne u dole navedeni interval pravila gibanja su:
[0, 0.2 ) → zapad,
[0.2, 0.4 ) → istok,
[0.4, 0.6 ) → sjever,
[0.6, 0.8 ) → jug,
[0.8, 1] → ostaje na mjestu
Rezultat računa će biti lista točaka kroz koje je prolazio mrav, tj. rezultat će biti putanja gibanja mrava.
Rješenje
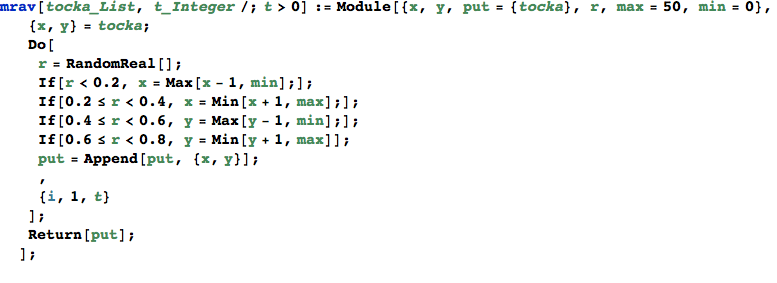
Testiranje
Ljubičasta točka označava točku iz koje mrav počinje gibanje a plava završnu točku gibanja.
Primjer simulacije ponašanja, "gibanje mrava", 2 varijanta
Zadatak
Mrav se giba, na slučajan način u kvadratu [0, 50]×[0, 50]. Gibanje počinje iz neke zadane točke i može se gibati u bilo kojem smijeru. Svaki izvedeni korak je duljine 1 i svaka od navedenih mogućnosti je jednako vjerojatna. Nacrtajte putanju gibanja mrava postije 2000 vremenskih intervala.
Pložaj mrava određen je koordinatama točke u kojoj se nalazi.
Slučajnost ćemo simulirati tako da će računalo generirati realan slučajan broj r između 0 i 2π što će zadati smjer u kojem će mrav zakoračiti.
Rezultat računa će biti lista točaka kroz koje je prolazio mrav, tj. rezultat će biti putanja gibanja mrava.
Označimo li sa 
) stari položaj mrava, a sa 
) novi položaj, tada vrijedi (trigonometrijska kružnica)
,
.
Rješenje
Testiranje
Ljubičasta točka označava točku iz koje mrav počinje gibanje a plava završnu točku gibanja.
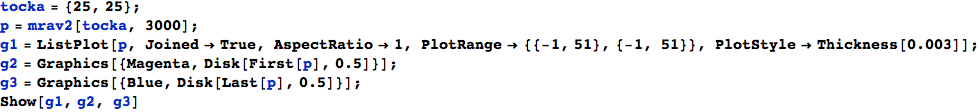
Notebook izradili: Vladimir Benić i Sonja Gorjanc
