,
},
,..}]
Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
8. predavanje
3D grafika
Funkcija Graphics3D - 3DPrimitivi
Funkcija Graphics3D omogućava, između ostalog, crtanje 3D primitiva
● Sintaksa za crtanje primitiva je sljedeća:
Graphics3D[ 2Dprimitiv ]
● Sintaksa za crtanje više primitiva je sljedeća:
Graphics3D[ { 2Dprimitiv 1, 2Dprimitiv 2,..... } ]
● Opcije za crtanje dodaju se na sljedeći način:
Graphics3D[ { opcija1,opcija2,....,2Dprimitiv } ]
3D primitivi
Point[{x,y,z}]
Točka s koordinatama (x,y,z).
Line[{{,},,..}]
Pravac ili više pravaca koji su spojnice točaka (
,
),
,..
Polygon[{{
,
,
},
,
,....}]
Prostorni poligon čiji su vrhovi redom točke (
,
),
,
,....
Cuboid[{
,
}]
Jedinična kocka kojoj je točka (
,
) jedan vrh.
Cuboid[{{
,
},
}]
Kvadratska prizma kojoj je spojnica točaka (
,
) i 
prostorna dijagonala.
Sphere[{x,y,z},r]
Kugla sa sredistem u točki (x,y,z) i polumjera r.
Cylinder[{{
,
,
},
},r]
Valjak kojem je spojnica točaka (
,
) i 
os, a polumjer r.
Text[tekst,{x,y,z}]
Ispisuje tekst koji je centriran u točku (x,y,z).
Primjeri
In[1]:=
Out[1]=
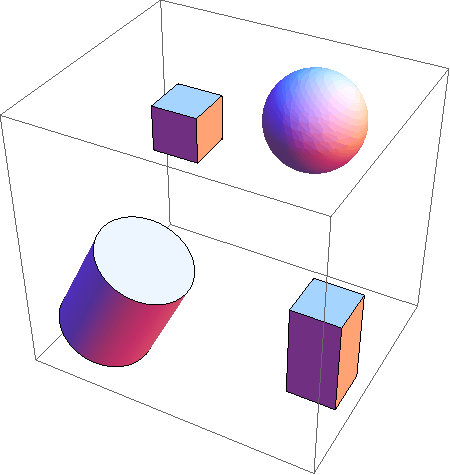
Uz dodatne opcije
In[2]:=
Out[2]=
Prodor dvaju valjaka
In[3]:=
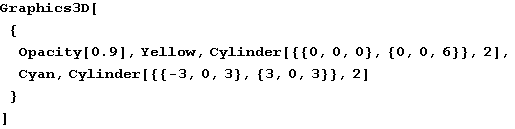
Out[3]=
In[4]:=
Out[4]=
Prodor valjka i kugle
In[5]:=
Out[5]=
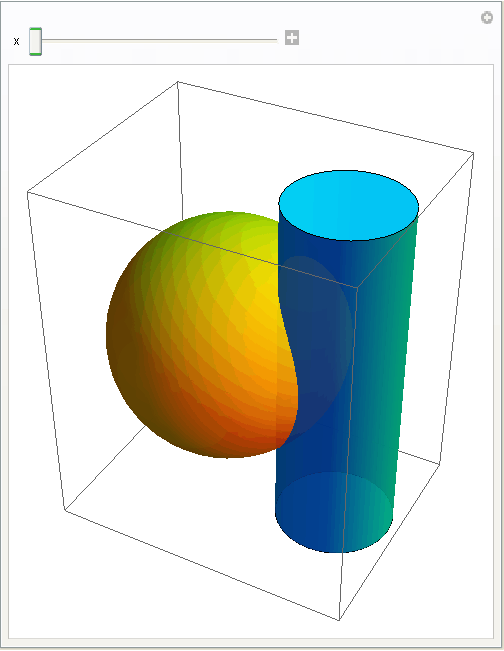
Funkcija Plot3D
Kao što smo već ranije spomenuli, Mathematica naredba koja omogućuje crtanje grafa realne funkcije dviju varijabli f : U → R, U⊆
,
tj. ploha zadanih eksplicitnim jednadžbama oblika z = f(x,y), je Plot3D.
Za crtanje jedne plohe sintaksa je
Plot3D [ f , {x,
,
}, {y,
,
} ],
a za crtanje više ploha
Plot3D [ 
, {x,
,
}, {y,
,
} ]
Primjer 1
Prikažite plohu zadanu jednadžbom z = cos
cos y za (x,y) ∈ 
In[6]:=
Out[6]=
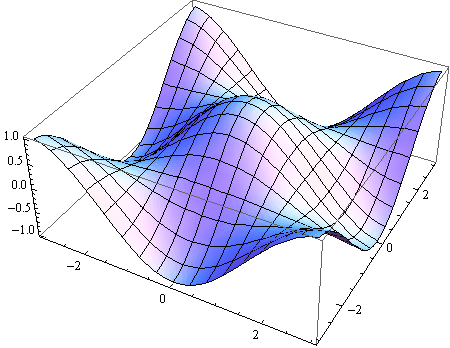
Opcije
In[7]:=
Out[7]=
Opcija BoxRatios
In[8]:=
Opcijom BoxRatios izražava se omjer stranica kocke u koju je ucrtana 3D slika.
BoxRatios→ {1,1,1} prikazuje grafiku unutar kocke
BoxRatios→ Automatic duljine osi odgovaraju stvarnim vrijednostima koordinata
In[9]:=
Out[9]=
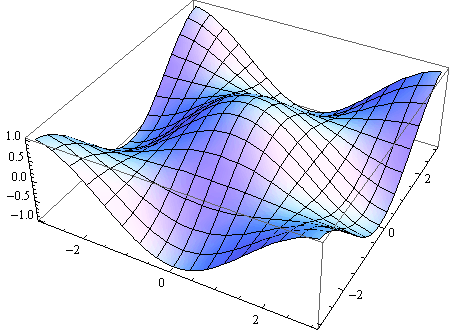
In[10]:=
Out[10]=
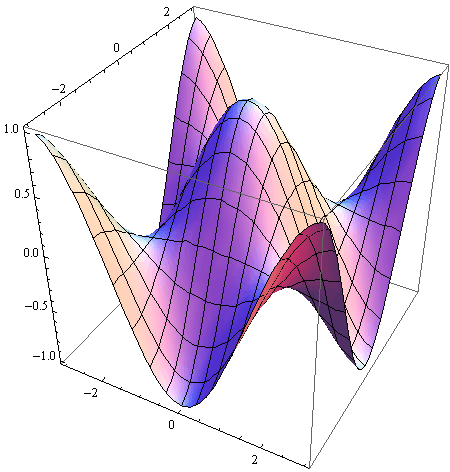
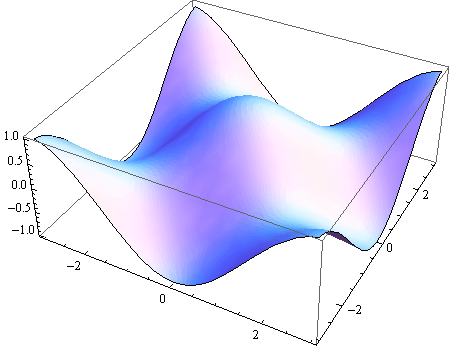
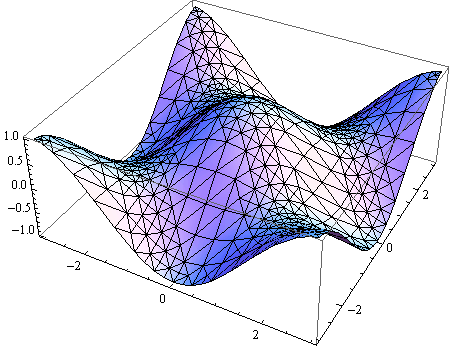
Opcije Mesh i MeshStyle
In[11]:=
Opcijom Mesh definira se iscrtavanje mreže linija na plohi.
In[12]:=
Out[12]=
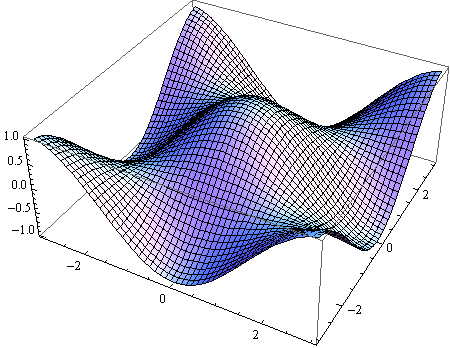
In[13]:=
Out[13]=
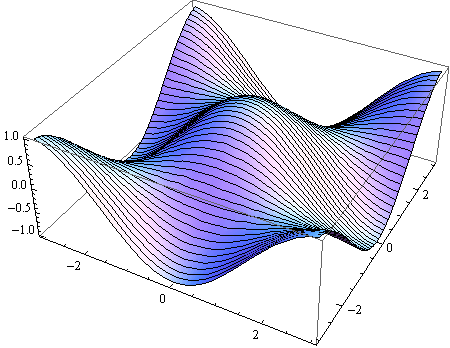
In[14]:=
Out[14]=
In[15]:=
Out[15]=
In[16]:=
Out[16]=
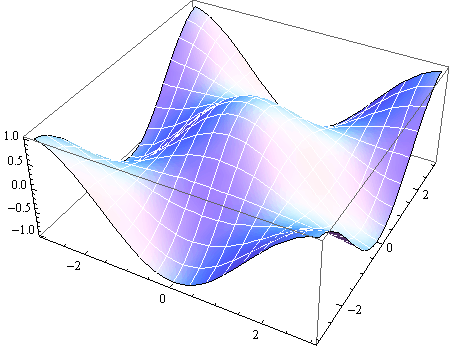
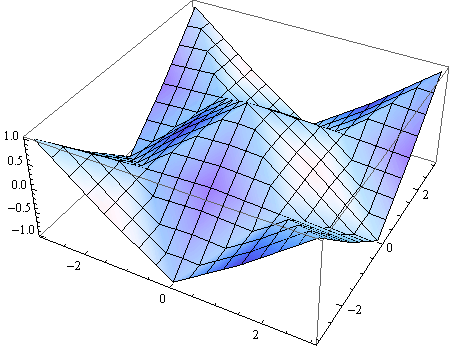
Opcija PlotPoints
In[17]:=
Opcijom PlotPoints definira se "finoća" grafike.
In[18]:=
Out[18]=
In[19]:=
Out[19]=
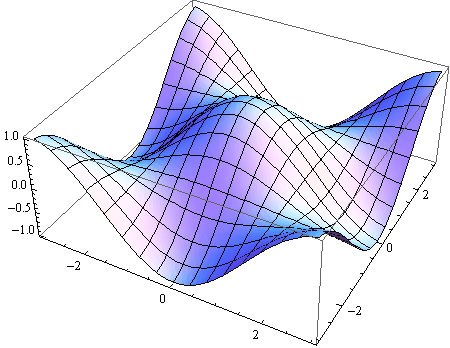
Opcija PlotRange
In[20]:=
Opcijom PlotRange definira dio prostora koji se prikazuje.
Ovu je opciju gotovo neophodno uportebljavati kod animacija.
In[21]:=
Out[21]=
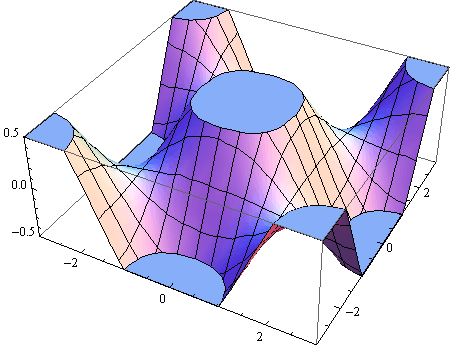
Opcija Boxed i Axes
In[22]:=
In[23]:=
In[24]:=
Out[24]=
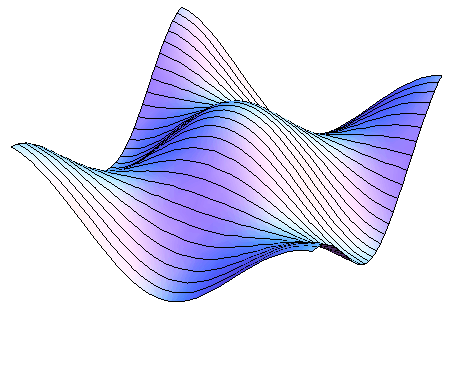
Opcija AxesLabel
In[25]:=
In[26]:=
Out[26]=
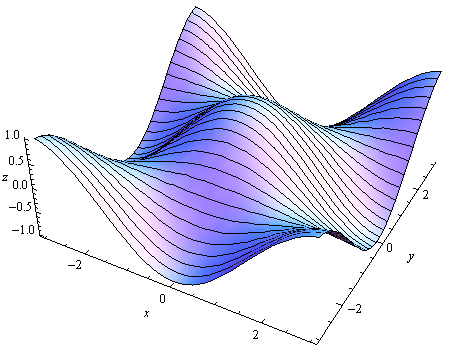
Opcija PlotStyle
In[27]:=
Pomoću ove opcije definiramo razne načine crtanja (boju, prozirnost, debljinu linija......), od kojih neke ovdje navodimo.
In[28]:=
Out[28]=
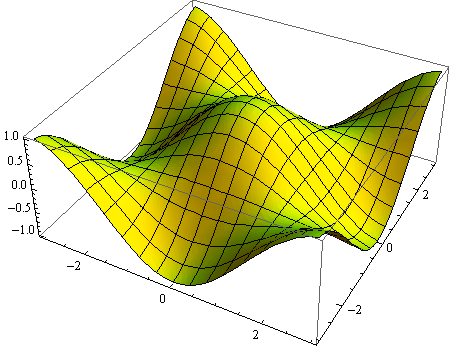
Opcija Opacity
In[29]:=
Opcijom Opacity definiramo prozirnost prikaza. Prozirnost određujemo brojem od 0 do 1, pri čemu 1 znači neprozirno.
Kod crtanja ploha uvijek ju pozivamo pomoću opcije PlotStyle.
In[30]:=
Out[30]=
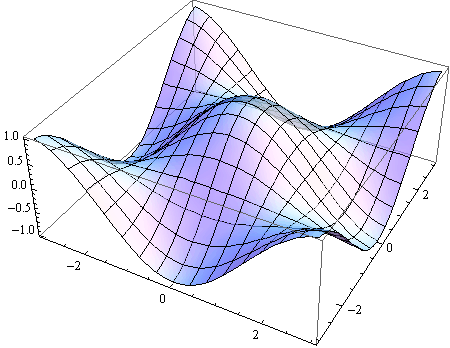
Možemo joj pridodati i boju.
In[31]:=
Out[31]=
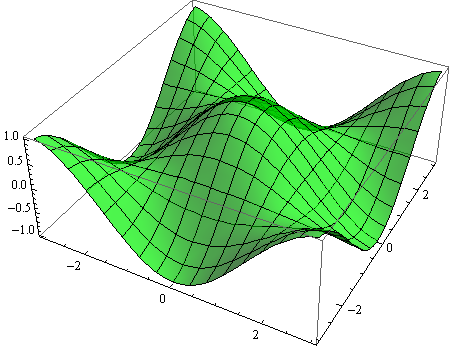
In[32]:=
Out[32]=
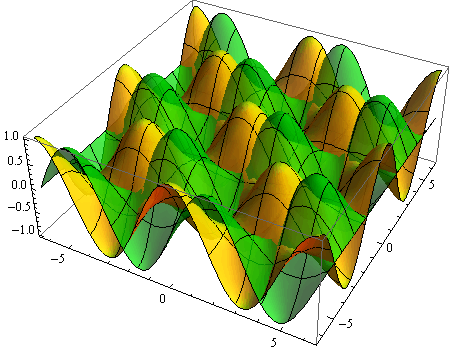
Opcija ColorFunction
In[33]:=
Opcijom ColorFunction određujemo koju će od svojih ugrađenih kolor funkcija Mathematika upotrijebiti za grafiku.
Lista tih funkcija nalazi se u paletama.
In[34]:=
Out[34]=
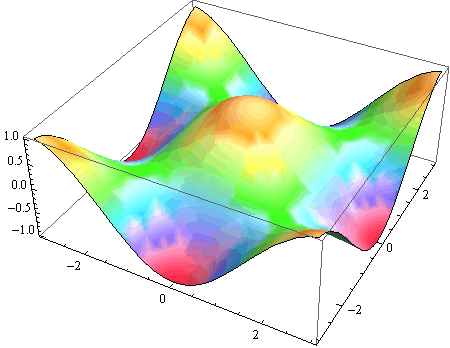
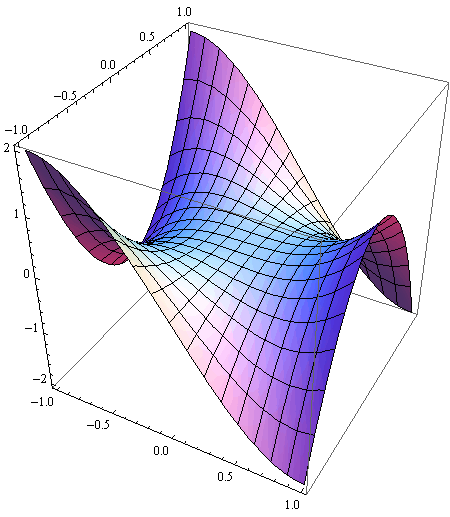
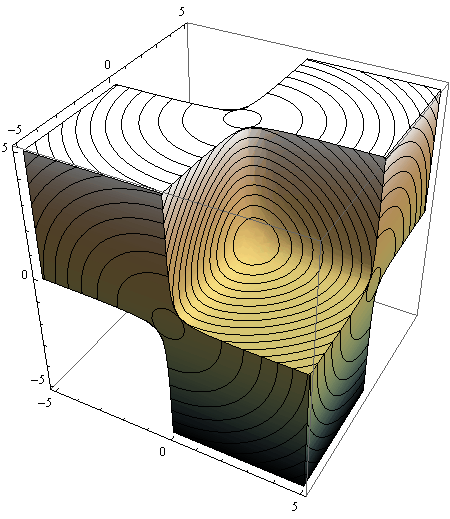
Primjer 2 - majmunsko sedlo
z = 
– 
In[35]:=
Out[35]=
In[36]:=
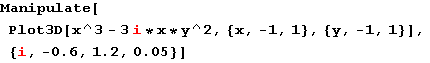
Out[36]=
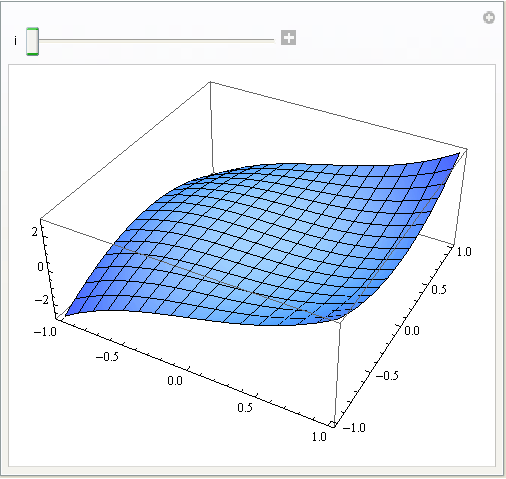
In[37]:=
Out[37]=
Funkcija ParametricPlot3D
1. Prostorne krivulje
Parametarizacija prostorne krivulje
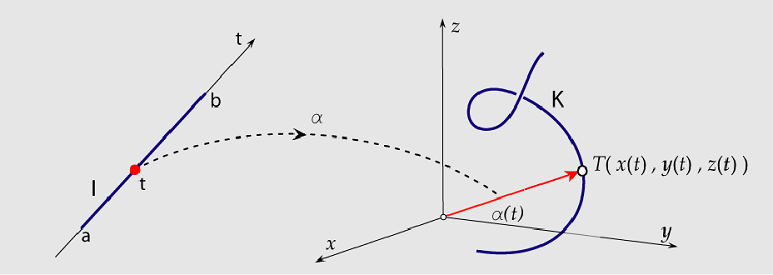
Mathematica funkcija koja omogućuje crtanje parametarski zadanih prostornih krivulja je ParametricPlot3D.
Za crtanje prostorne krivulje zadane parametarskim jednadžbama
= x(t)
= y(t)
= z(t), t ε I ⊆ R
sintaksa je sljedeća:
ParametricPlot3D[{
,
,
}, {t,
,
}]
Za crtanje više parametarski zadanih krivulja na istom crtežu sintaksa je sljedeća:
ParametricPlot3D[{{
,
,
},{
,
,
},.....}, {t,
,
}]
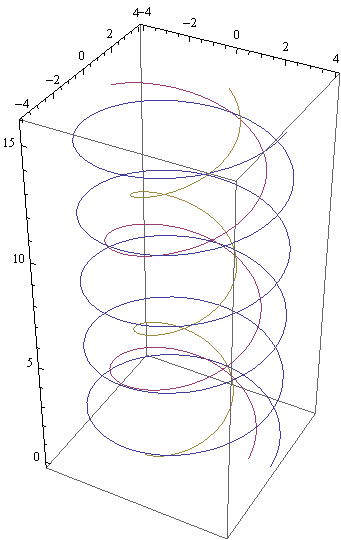
Primjer — zavojnica na valjku
Parametarske jednadžbe zavojnice na rotacijskom valjku kojem je os paralelna s osi z, a polumjer osnovice jednak r, su:
x = r·cost
y = r·sint
z = b·t, t ∈ I ⊆ R.
In[38]:=
Out[38]=
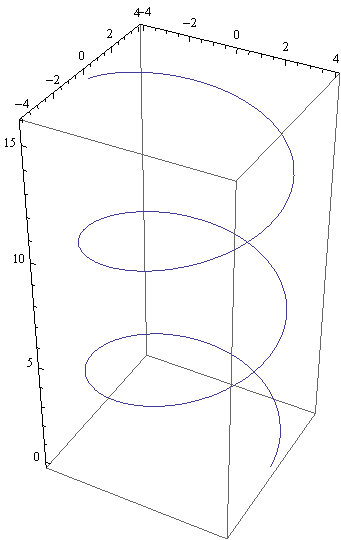
In[39]:=
Out[39]=
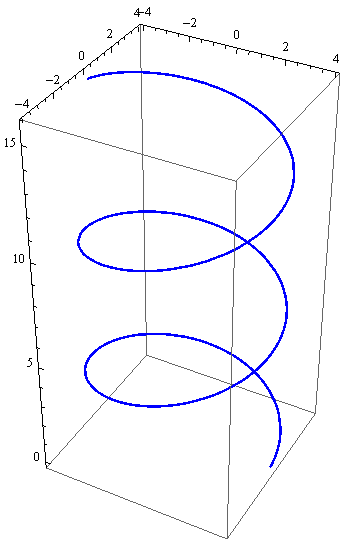
In[40]:=
Out[40]=
2. Plohe
Parametarizacija plohe
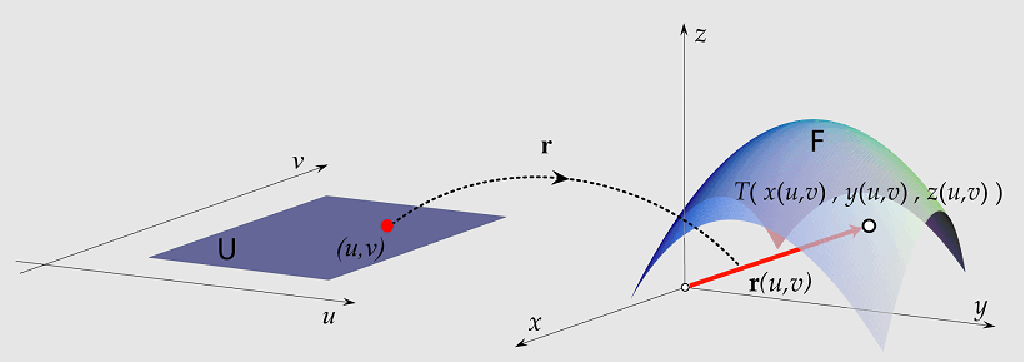
Mathematica funkcija koja omogućuje crtanje parametarski zadanih ploha je ParametricPlot3D.
Za crtanje plohe zadane parametarskim jednadžbama
= x(u,v)
= y(u,v)
= z(u,v), (u,v) ε U ⊂ 
sintaksa je sljedeća:
ParametricPlot3D[{
,
,
}, {u,
,
},{v,
,
}]
Za crtanje više parametarski zadanih ploha na istom crtežu sintaksa je sljedeća:
ParametricPlot3D[{{
,
,
},{
,
,
},.....}, {u,
,
},{v,
,
}]
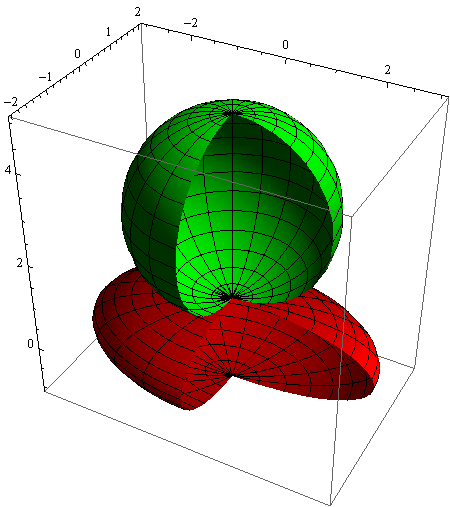
Primjeri 1 — kugla i elipsoid
Parametarske jednadžbe kugle polumjera R, sa središtem u točki (p,q,r) su:
x = R·cosu·sinv + p
y = R·sinu·sinv + q
z = R·cosv + r, (u,v) ∈ [0 , 2π] × [0 , π].
Parametarske jednadžbe troosnog elipsoida sa središtem u točki (p,q,r) su:
x = a·cosu·sinv + p
y = b·sinu·sinv + q
z = c·cosv + r, (u,v) ∈ [0 , 2π] × [0 , π].
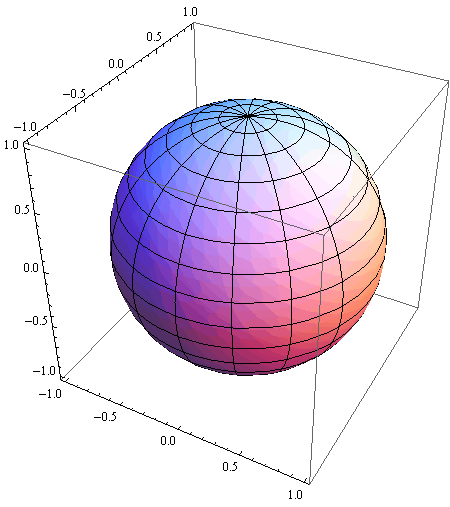
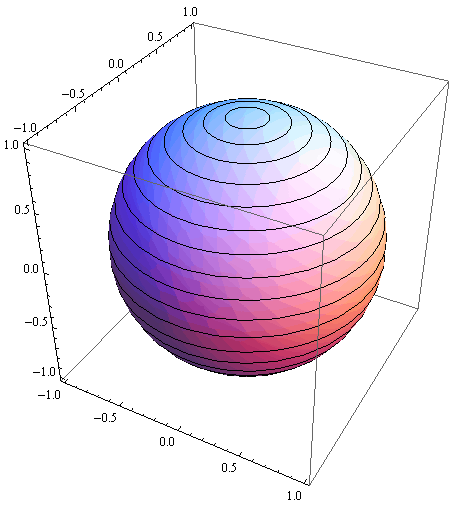
Stoga je naredba za crtanje jedinične kugle sa središtem u ishodištu sljedeća:
In[41]:=
Out[41]=
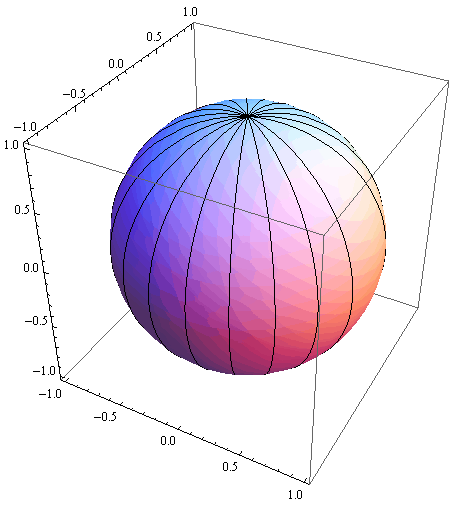
In[42]:=
Out[42]=
In[43]:=
Out[43]=
In[44]:=
In[45]:=
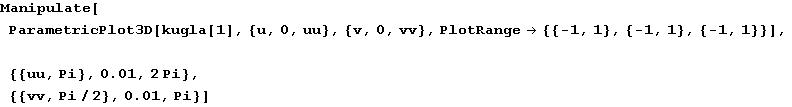
Out[45]=
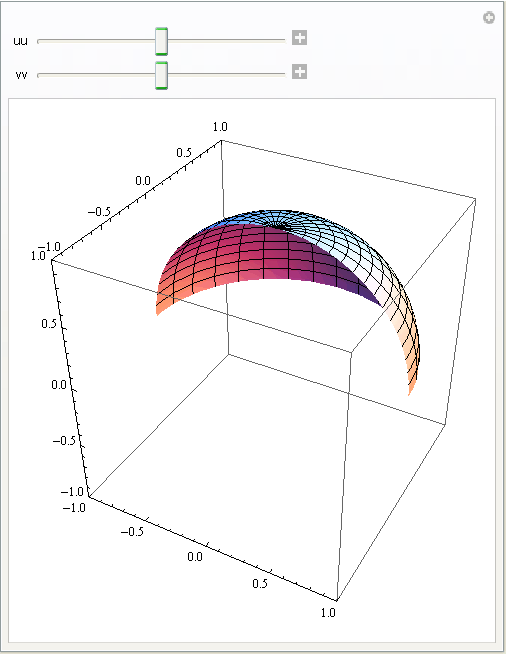
In[46]:=
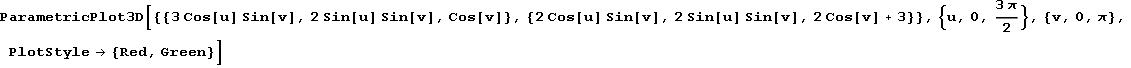
Out[46]=
In[47]:=
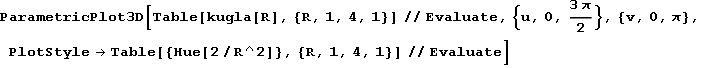
Out[47]=
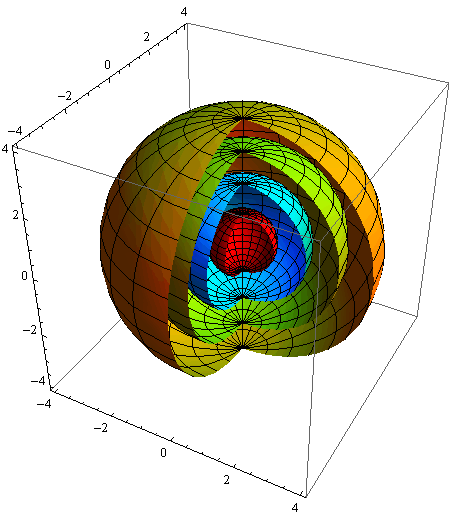
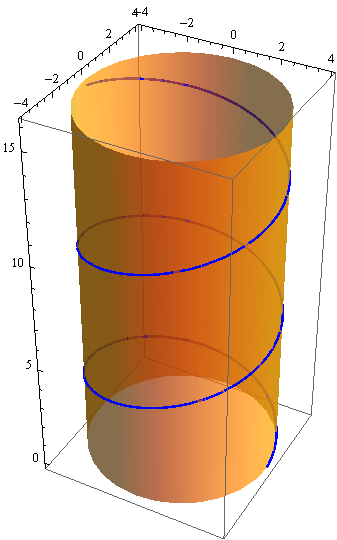
Primjer 2 — kružni valjak
In[48]:=
Out[48]=
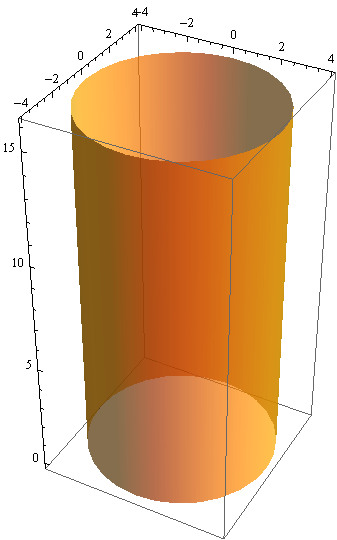
In[49]:=
Out[49]=
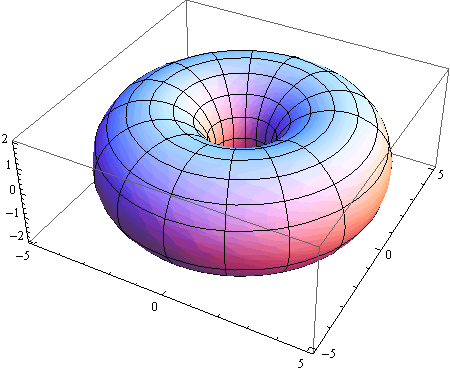
Primjeri 3 — torus
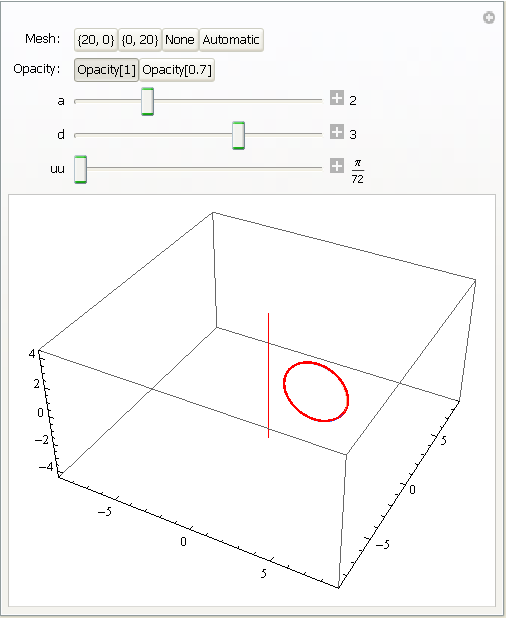
Torus je ploha koja nastaje rotacijom kružnice polumjera a oko osi koja je od središta te kružnice udaljena za d.
Ako kružnica leži u ravnini xz i rotira oko osi z, parametarske jednadžbe torusa su:
x = cosu (d + a·cosv )
y = sinu (d + a·cosv )
z = a·sinv, (u,v) ∈ [0 , 2π] × [0 ,2 π].
In[50]:=
Stoga je naredba za crtanje jedinične kugle sa središtem u ishodištu sljedeća:
In[51]:=
Out[51]=
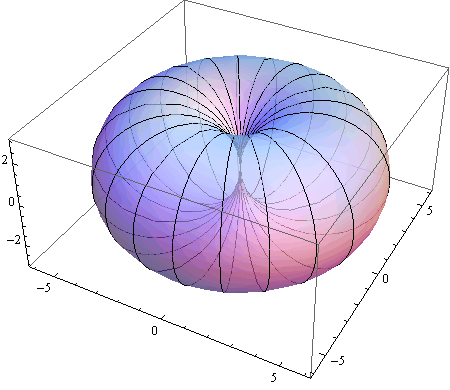
In[52]:=
Out[52]=
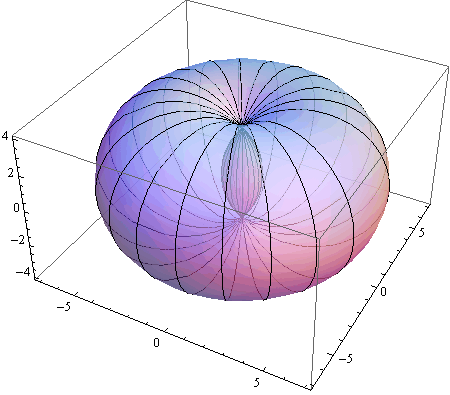
In[53]:=
Out[53]=
In[54]:=
Out[54]=
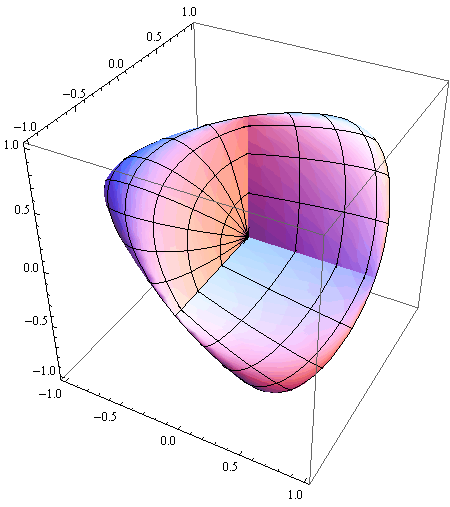
Primjer 4 — Steinerova ploha
Steinerova ploha je algebarska ploha 4. reda s 4 dvostruka pravca, koja se može parametrizirati na sljedeći način:
x = sin2u ·
y = sinu sin2v
z = cosu sin2v, (u,v) ∈ [0 , π] × [0 , π].
In[55]:=
In[56]:=
Out[56]=
In[57]:=
Out[57]=
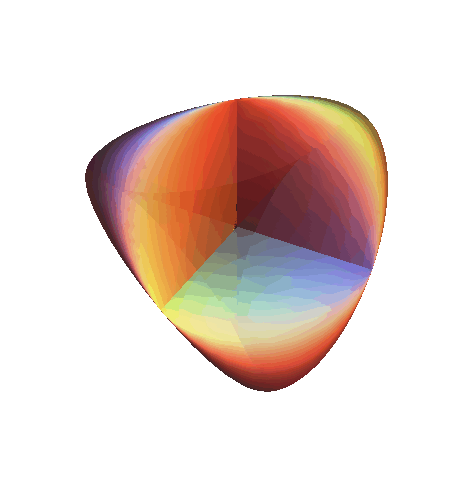
Funkcija ContourPlot3D
Funkcije ContourPlot3D omogućuju crtanje nivo-ploha za funkcije od tri varijable.
U okviru ovog kolegija mi ćemo ju koriprostornom Kartezijevom koordinatnom sustavu zadane implicitnim jednadžbama, tj. jednadžbama oblika:
f(x,y,z)=0.
Sintaksa je sljedeća:
ContourPlot3D[ jednadžba , {x,
,
},{y,
,
},{z,
,
}]
ContourPlot3D[
,
,.......}, {x,
,
},{y,
,
},{z,
,
}]
Kod ove funkcije Mathematica će kao temeljnu opciju za prikaz uzimati BoxRatios -> {1,1,1}, tj. plohu će prikazivati unutar kocke. Želimo li da jedinice na osima budu jednake proporcije, a to nam je često potrebno, treba dopisatii opciju BoxRatios -> Automatic.
Primjer 1
ALGEBARSKE PLOHE 2. STUPNJA
KUGLA
In[58]:=
Out[58]=
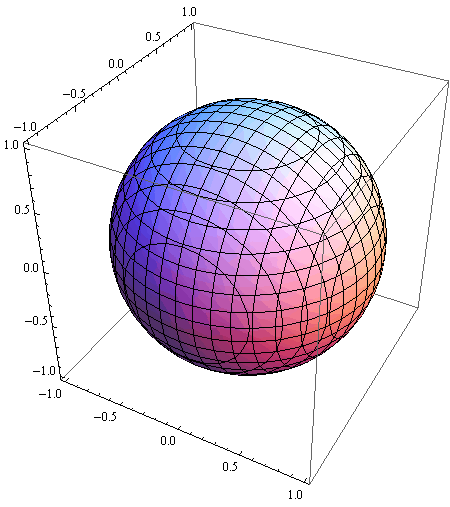
In[59]:=
Out[59]=
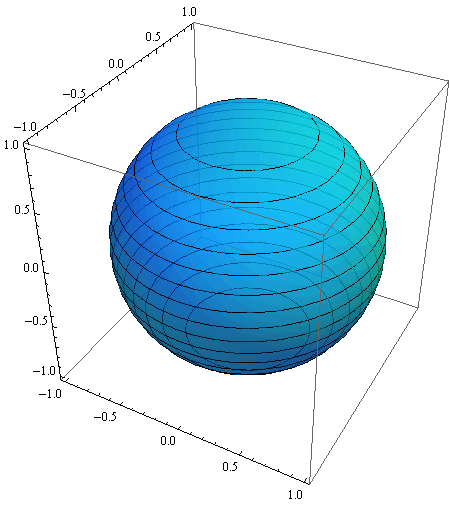
In[60]:=
Out[60]=
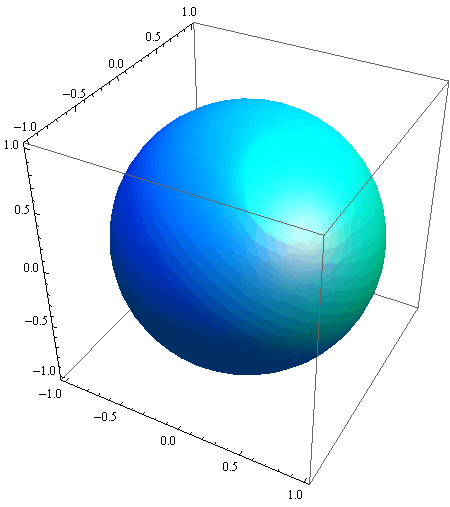
In[61]:=
Out[61]=
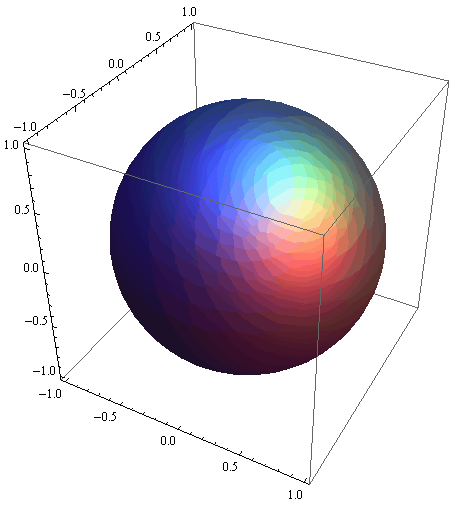
ELIPSOID
In[62]:=
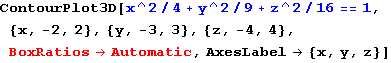
Out[62]=
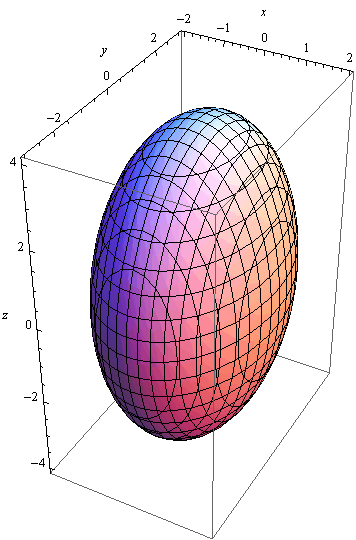
JEDNODIJELNI HIPERBOLOID
In[63]:=
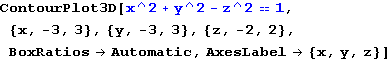
Out[63]=
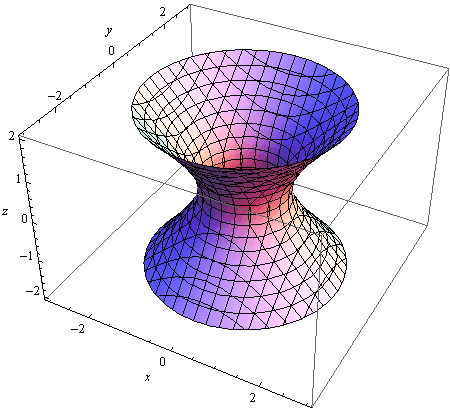
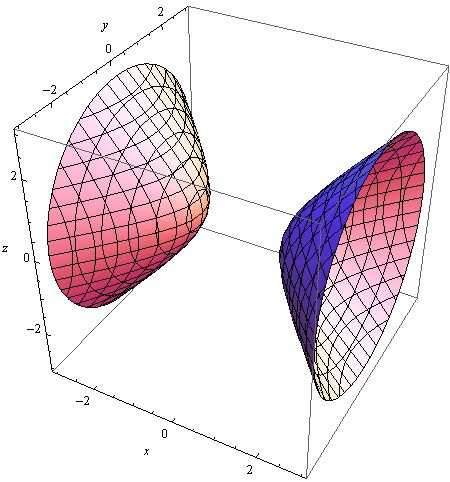
DVODIJELNI HIPERBOLOID
In[64]:=
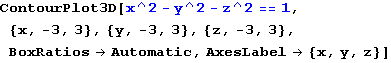
Out[64]=
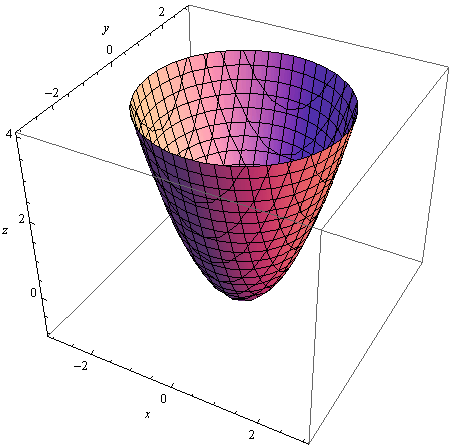
PARABOLOID
In[65]:=
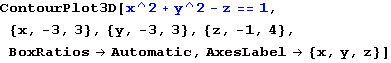
Out[65]=
HIPERBOLIČKI PARABOLOID
In[66]:=
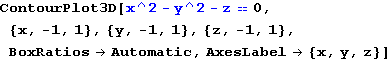
Out[66]=
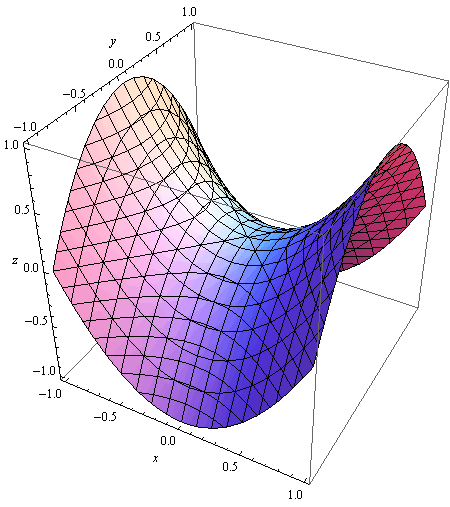
STOŽAC
In[67]:=
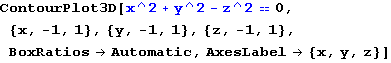
Out[67]=
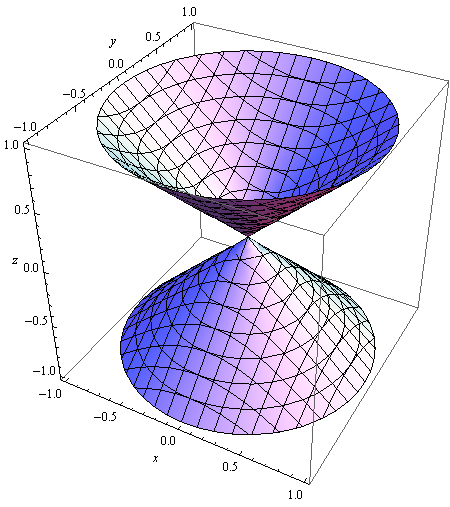
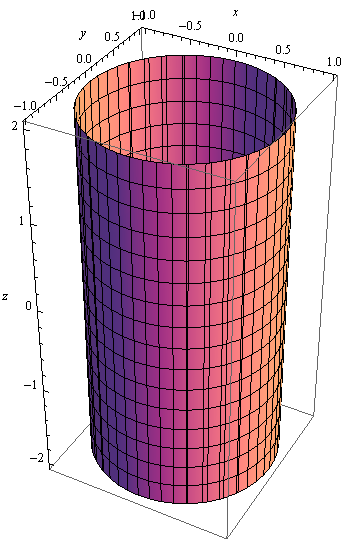
VALJAK
In[68]:=
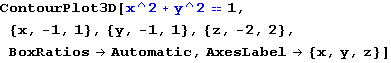
Out[68]=
Primjer 2
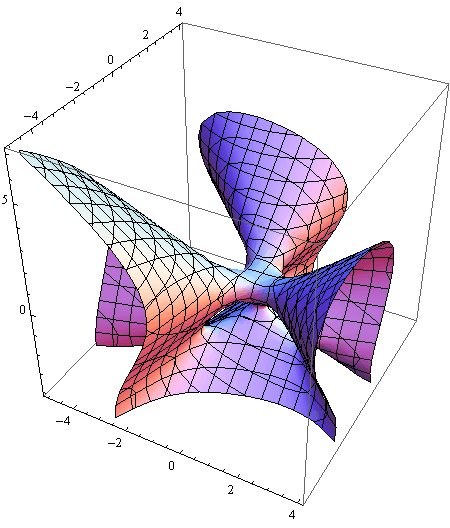
Algebarska ploha 3. reda zadana je jednadžbom:
Prikažite ju za (x,y,z) ∈ 
In[69]:=
In[70]:=
Out[70]=
In[71]:=
Out[71]=
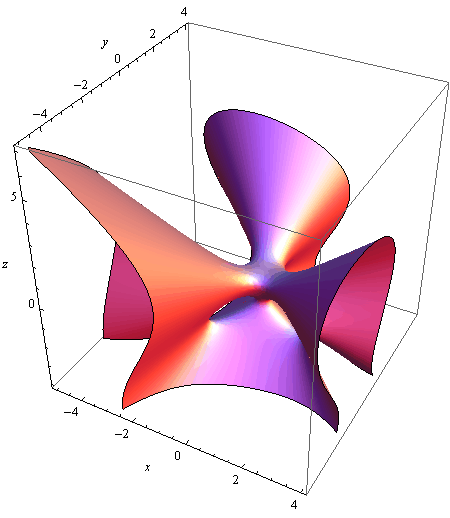
Primjer 3
Algebarska ploha 4. reda s 8 dvostrukih točaka zadana je jednadžbom:
Prikažite ju za (x,y,z) ∈ 
In[72]:=
In[73]:=
Out[73]=
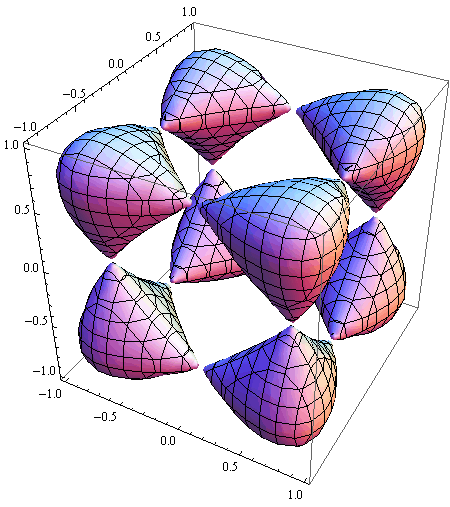
In[74]:=
Out[74]=
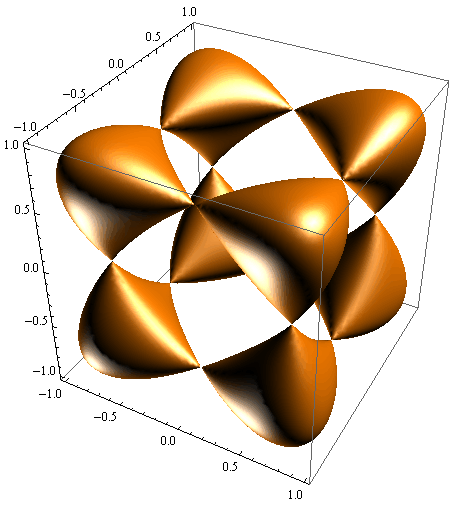
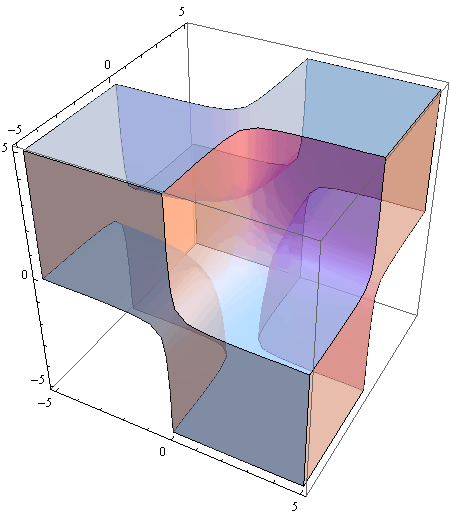
Funkcija RegionPlot3D
Za grafički prikaz rješenja nejednadžbi od 3 varijable koristimo funkciju RegionPlot3D.
Sintaksa je sljedeća:
RegionPlot3D[ izraz, {x,
,
},{y,
,
},{z,
,
}]
Mathematica prikazuje dio prostora unutar kvadra (
,
)×(
,
)×(
,
) za koji vrijedi izraz.
izraz može biti bilo koja nejednadžba od tri varijable (x, y i z) ili logička kombinacija takvih nejednadžbi.
Primjeri
In[75]:=
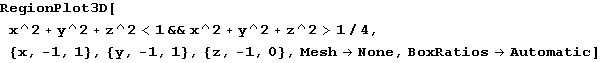
Out[75]=
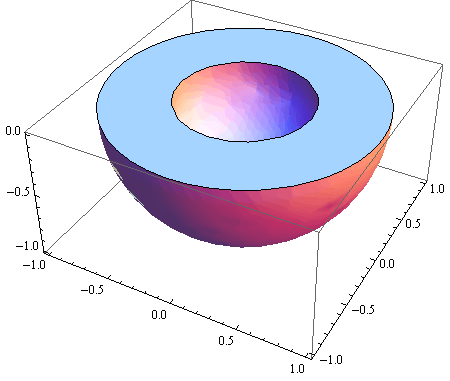
In[76]:=
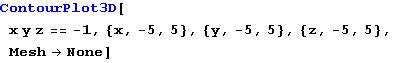
Out[76]=
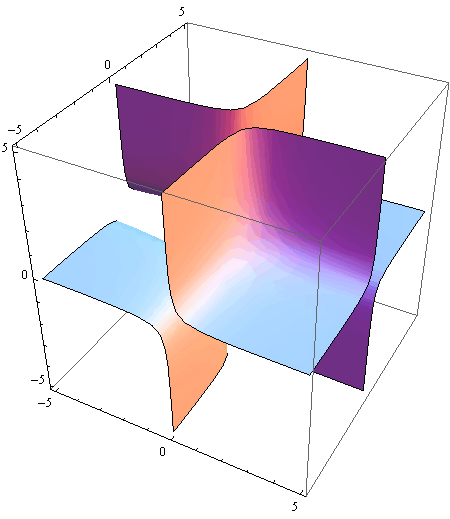
In[77]:=
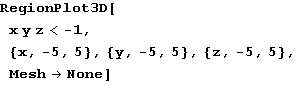
Out[77]=
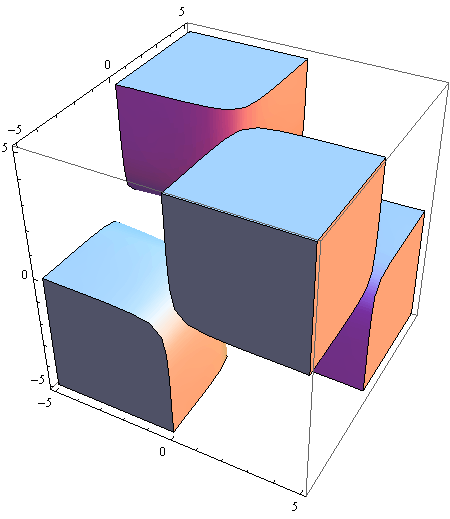
In[78]:=
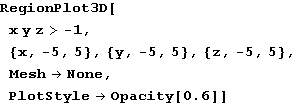
Out[78]=
In[79]:=
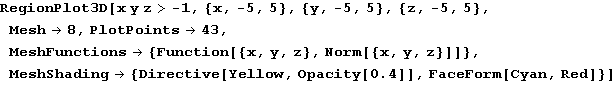
Out[79]=
In[80]:=
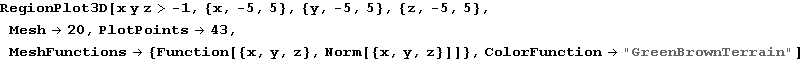
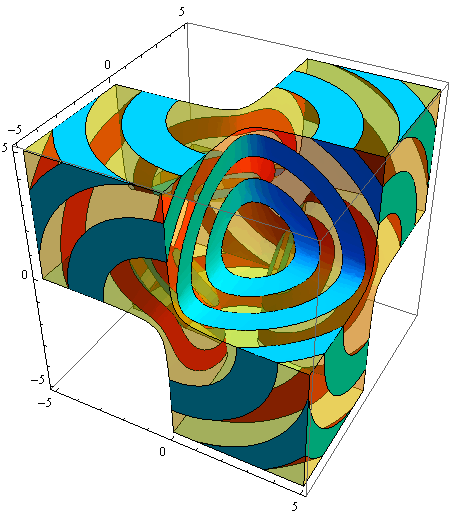
Out[80]=
Notebook izradili: Sonja Gorjanc, Vladimir Benić
