,
},
,..}]
Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
7. predavanje
2D grafika
Funkcija Graphics - 2DPrimitivi
Funkcija Graphics, između ostalog, omogućuju crtanje 2D primitiva,
● Sintaksa za crtanje primitiva je sljedeća:
Graphics[ 2Dprimitiv ]
● Sintaksa za crtanje više primitiva je sljedeća:
Graphics[ { 2Dprimitiv 1, 2Dprimitiv 2,..... } ]
● Opcije za crtanje dodaju se na sljedeći način:
Graphics[ { opcija1,opcija2,....,2Dprimitiv } ]
2D primitivi
Point[{x,y}]
Točka s koordinatama (x,y).
Line[{{,},,..}]
Pravac ili više pravaca koji su spojnice točaka (
,
),
,..
Arrow[{{
,
},
}]
Strijelica na kraju spojnice točaka (
,
) i 
.
Polygon[{{
,
},
,
,....}]
Poligon čiji su vrhovi redom točke (
,
),
,
,....
Rectangle[{{
,
},
}]
Kvadrat kojem su točke (
,
) i 
krajnje jedne dijagonale.
Circle[{x,y},r]
Kružnica s koordinatama središta (x,y) i polumjerom r.
Disk[{x,y},r]
Krug s koordinatama središta (x,y) i polumjerom r.
Text[tekst,{x,y}]
Ispisuje tekst koji je centriran u točku (x,y).
Primjeri
In[1]:=
Out[1]=
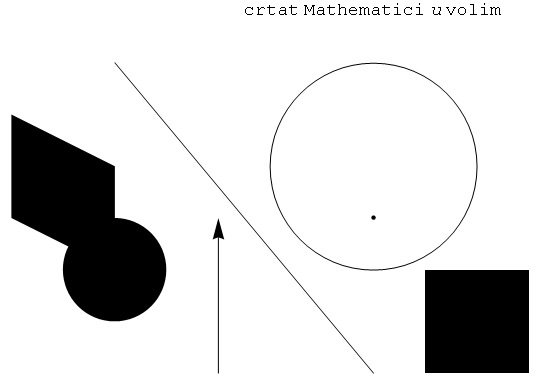
Uz dodatne opcije
In[2]:=
Out[2]=
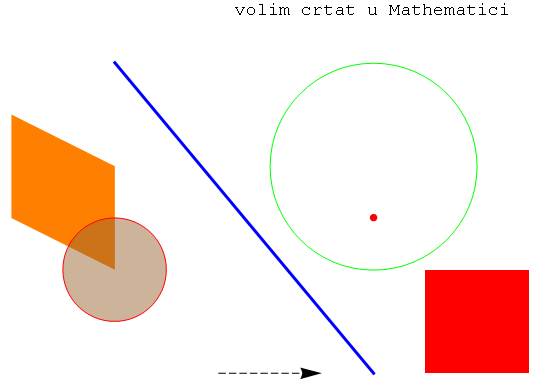
Funkcija Plot
Ovu funkcija, koja omogućuje crtanje grafa eksplicitno zadane funkcije jedne varijable y=f(x), upoznali ste na 3. predavanju i do sada ju koristili u većem broju primjera. Preko nje ste naučili osnove sintakse Mathematica naredbi za crtanje te neke grafičke opcije (AspectRatio, PlotStyle, AxesLabel, Filling i dr.)
Te ćete opcije, kao i mnoge druge, moći koristiti i u gotovo svim ostalim Mathematica funkcijama za crtanje ravninskih krivulja.
Funkcija ParametricPlot
Mathematica funkcija koja omogućuje crtanje parametarski zadanih krivulja je ParametricPlot.
Za crtanje krivulje zadane parametarskim jednadžbama
= x(t)
= y(t), t ε I ⊂ R
sintaksa je sljedeća:
ParametricPlot [ {
,
} , {t,
,
} ]
Za crtanje više parametarski zadanih krivulja na istom crtežu sintaksa je sljedeća:
ParametricPlot [ {{
,
},{
,
},.....} , {t,
,
} ]
Primjeri 1
Jedinična kružnica sa središtem u ishodištu.
In[3]:=
Out[3]=
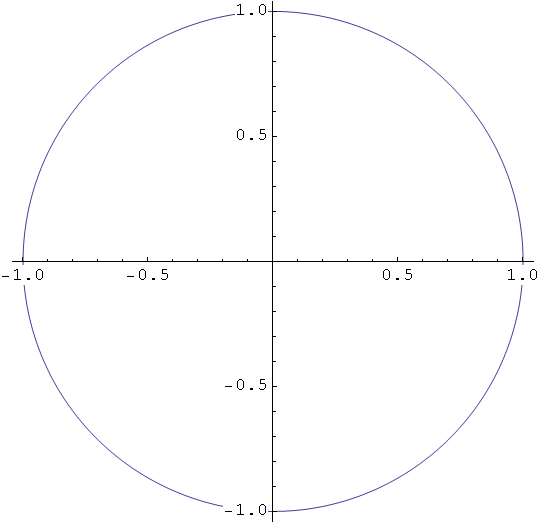
Elipsa s poluosima a, b i koordinatama središta (p,q).
In[4]:=
Out[4]=
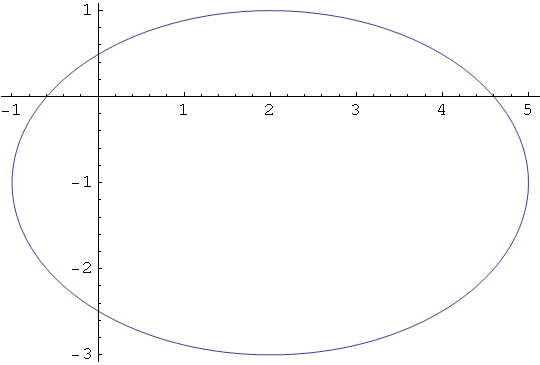
In[5]:=
In[6]:=
Out[6]=
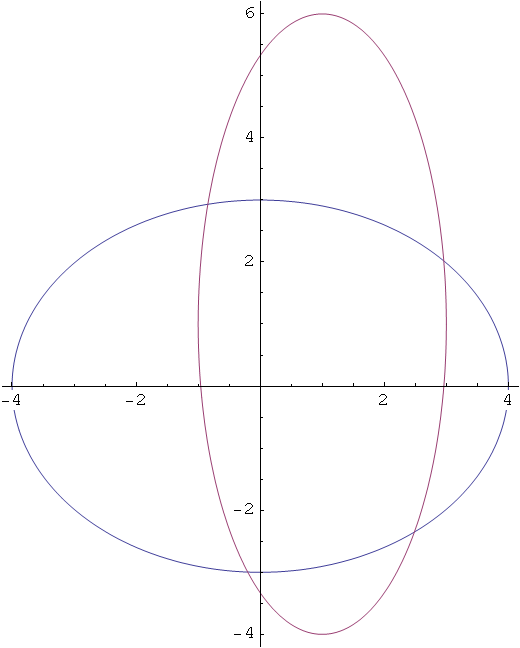
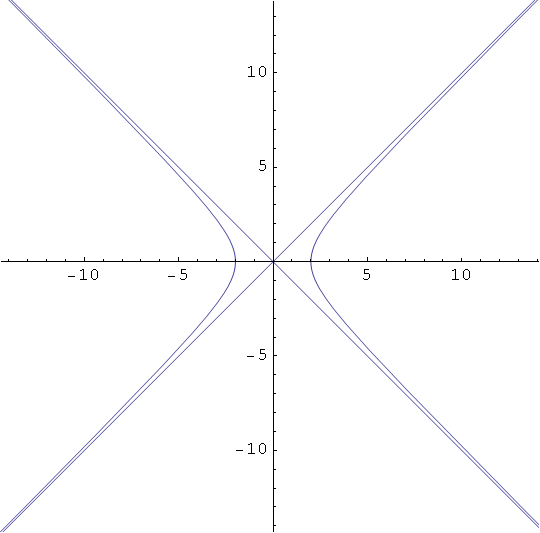
Hiperbola s poluosima a, b i koordinatama središta (p,q).
In[7]:=
In[8]:=
Out[8]=
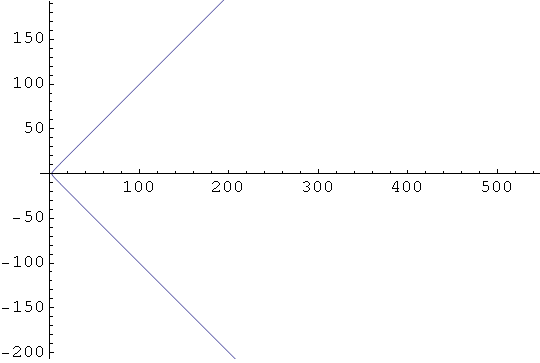
Upotrijebimo opciju PlotRange
In[9]:=
Out[9]=
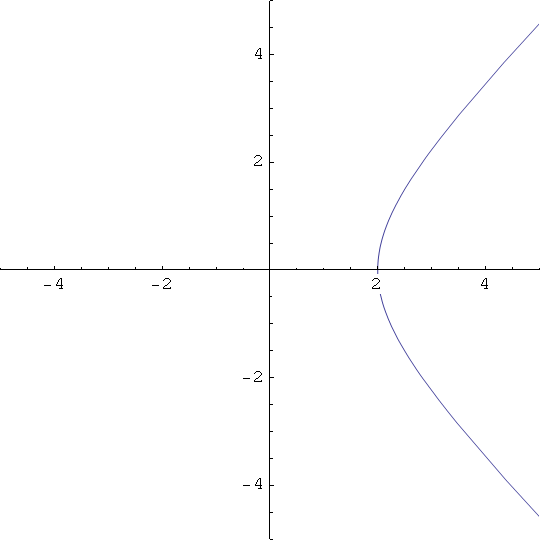
In[10]:=
Out[10]=
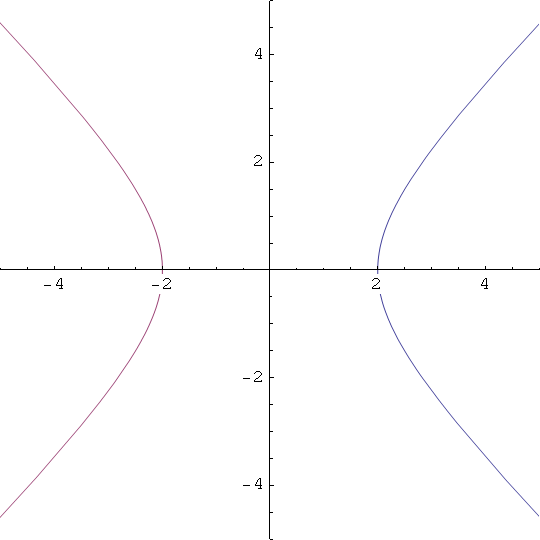
In[11]:=
In[12]:=
Out[12]=
Primjeri 2
Cikloida
In[13]:=
In[14]:=
Out[14]=
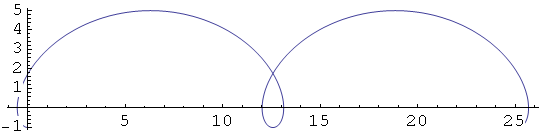
In[15]:=
Out[15]=
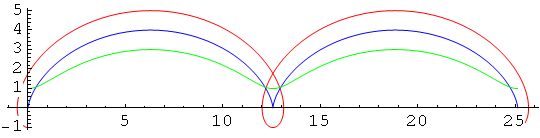
ANIMACIJA izvođenja cikloide
In[16]:=
In[27]:=
Out[27]=
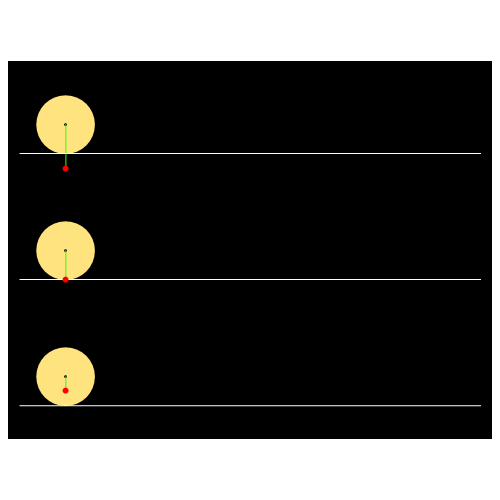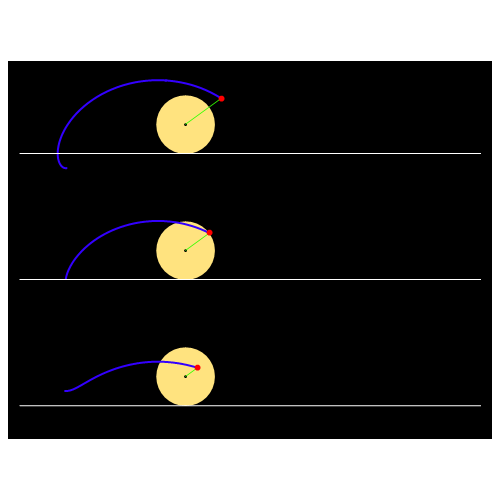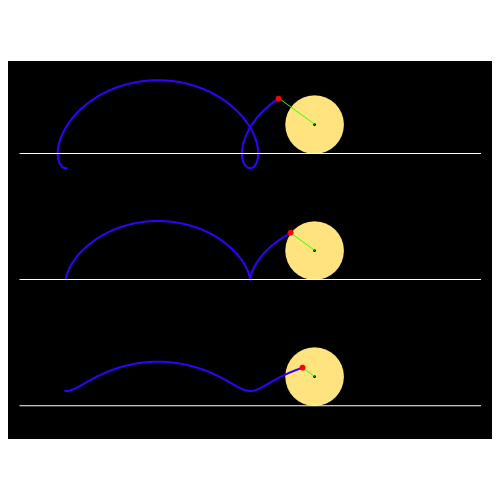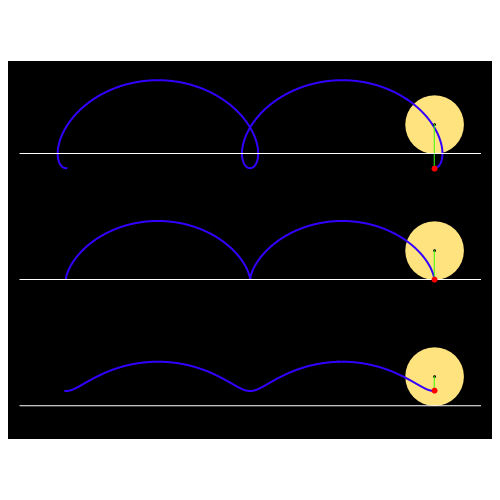
Funkcija PolarPlot
Mathematica funkcija koja omogućuje crtanje ravninskih krivulja koje su u polarnom koordinatnom sustavu (r,φ) dane jednadžbama oblika r = r(φ) je PolarPlot.
Sintaksa za korištenje te naredbe je sljedeća:
PolarPlot[ r(φ), {φ,
,
}]
Za crtanje više krivulja na istom crtežu sintaksa je sljedeća:
PolarPlot [ {
(φ),
,.....} , {φ,
,
}]
Primjeri
Kružnica
In[28]:=
Out[28]=
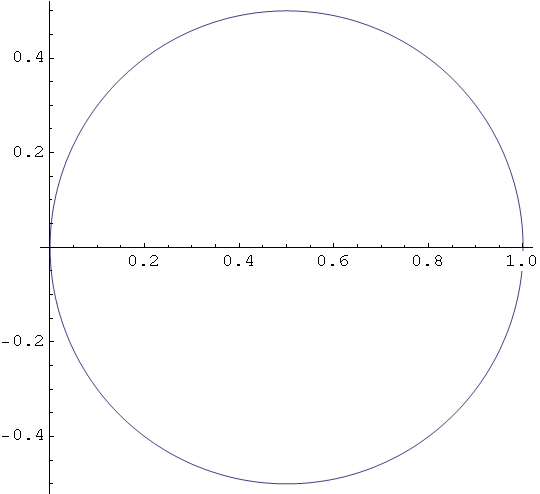
In[29]:=
Out[29]=
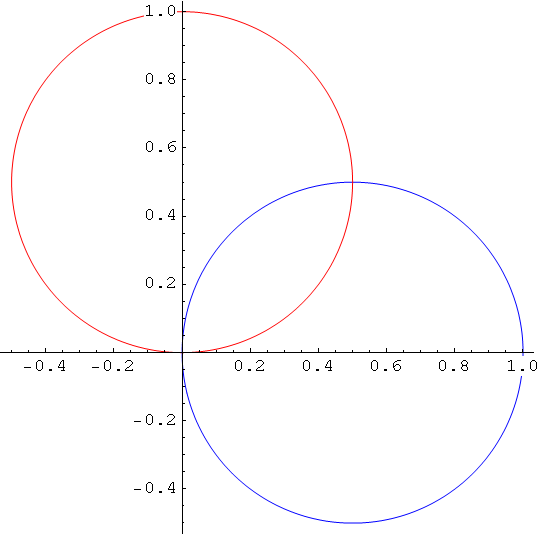
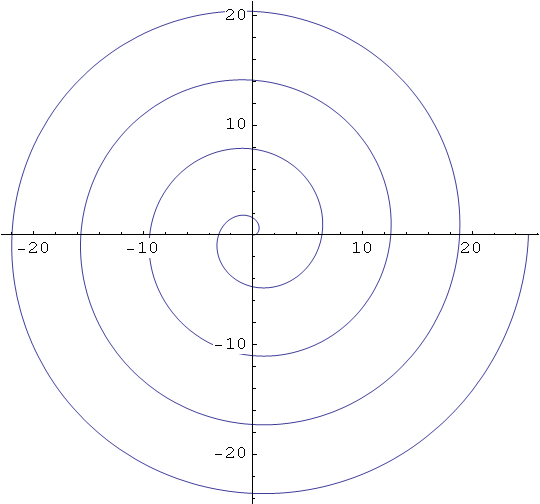
Arhimedova spirala
In[30]:=
In[31]:=
Out[31]=
In[32]:=
Out[32]=
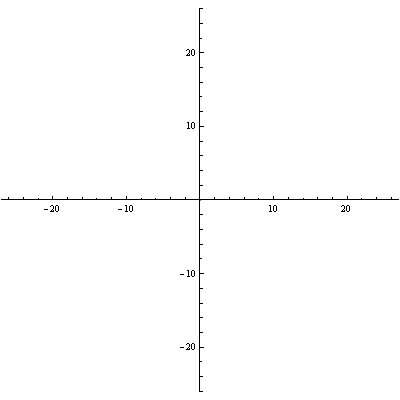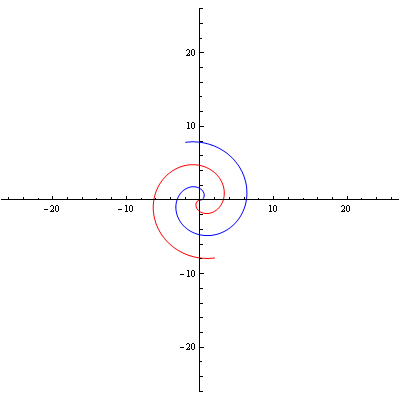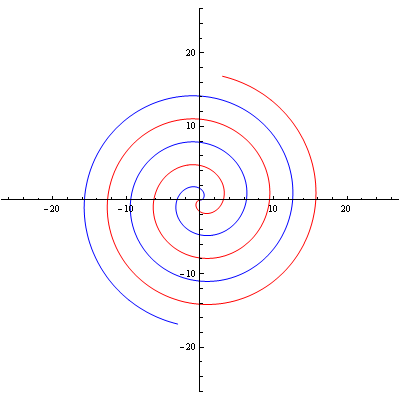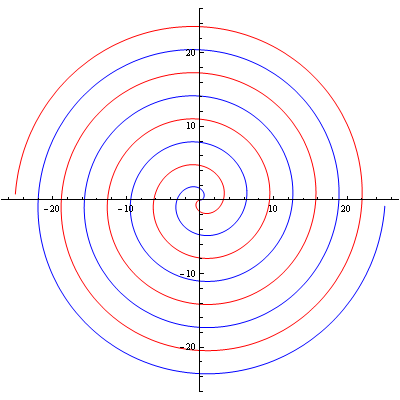
In[33]:=
Out[33]=
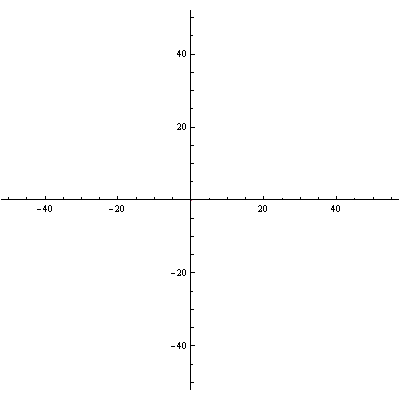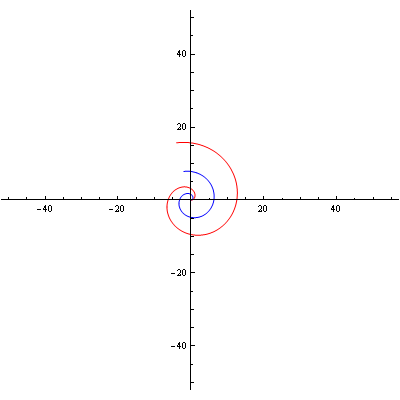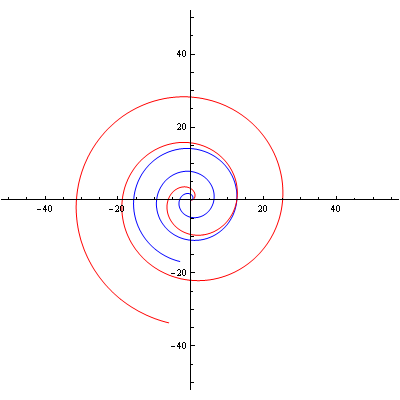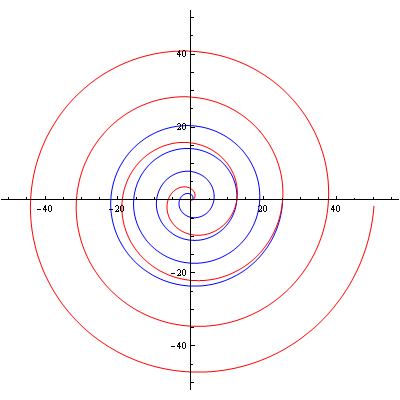
Logaritamska spirala
In[34]:=
In[35]:=
Out[35]=
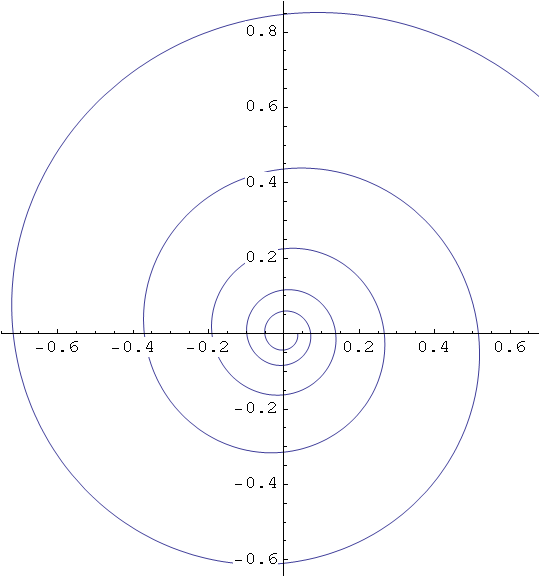
In[36]:=
Out[36]=
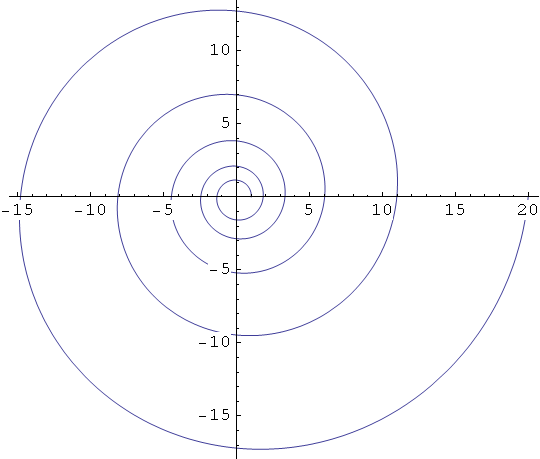
In[37]:=
Out[37]=
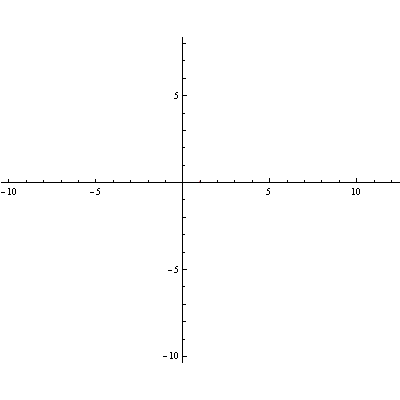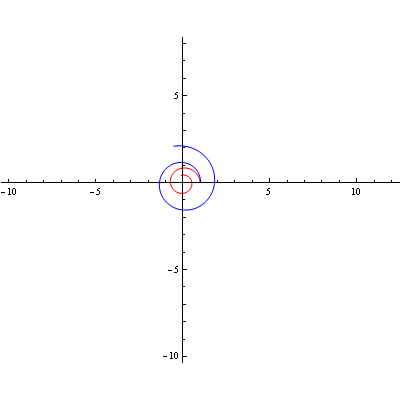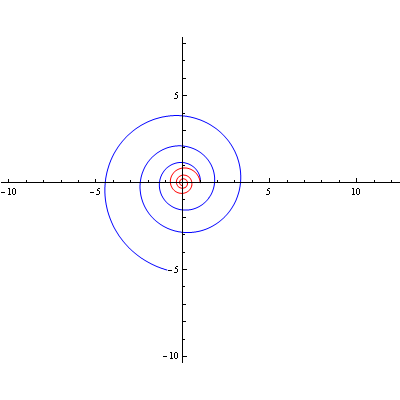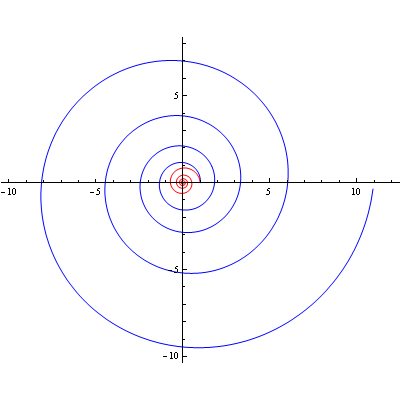
Primjer rotacije
In[38]:=
Out[38]=
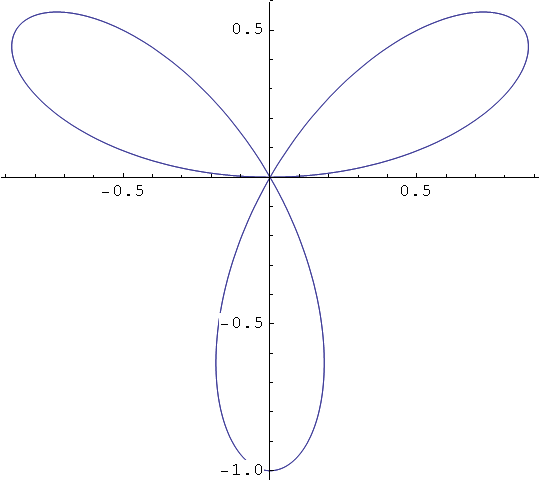
In[39]:=
Out[39]=
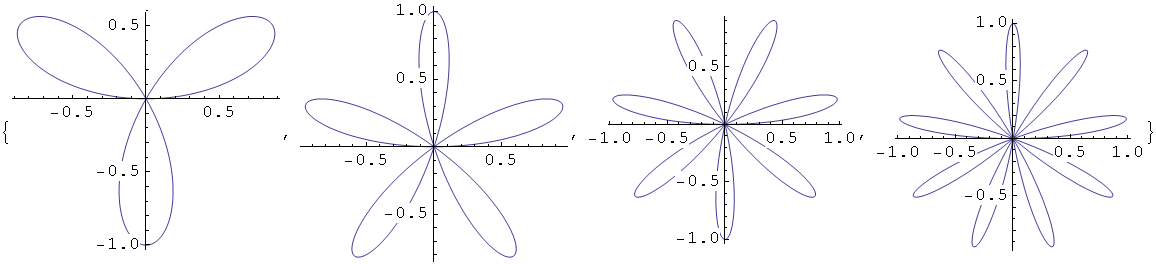
In[40]:=
Out[40]=
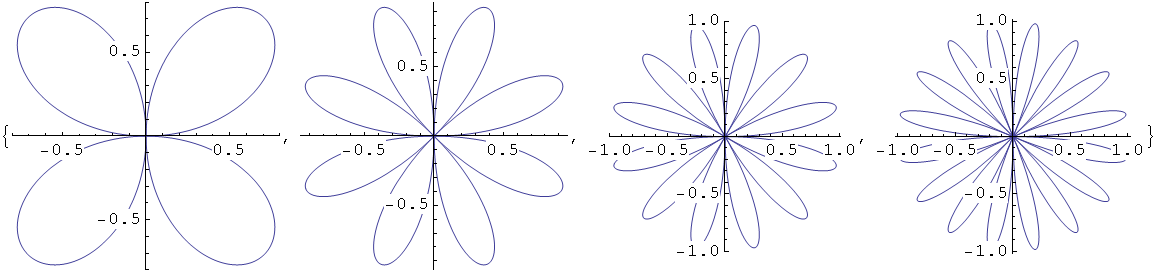
In[41]:=
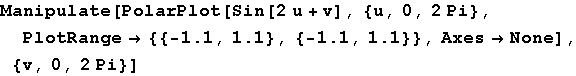
Out[41]=
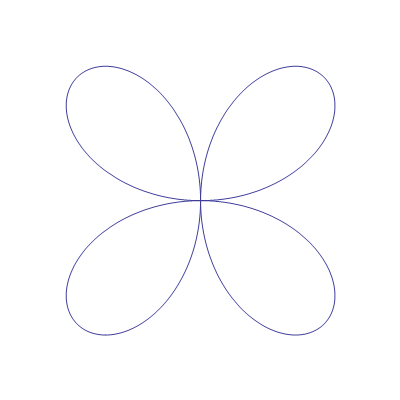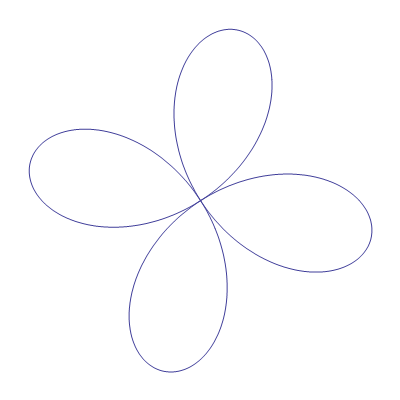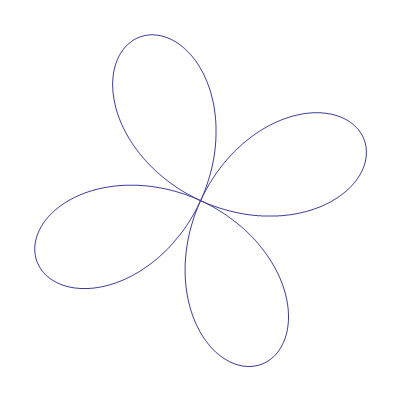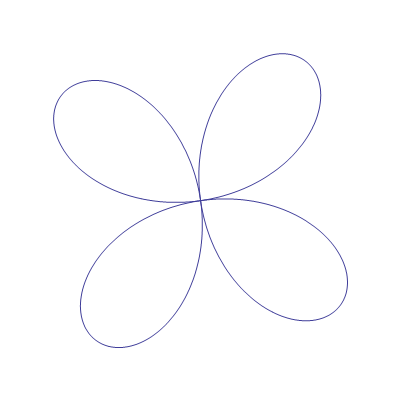
In[42]:=
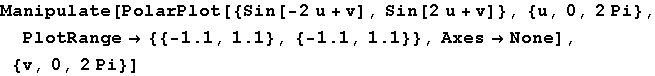
Out[42]=
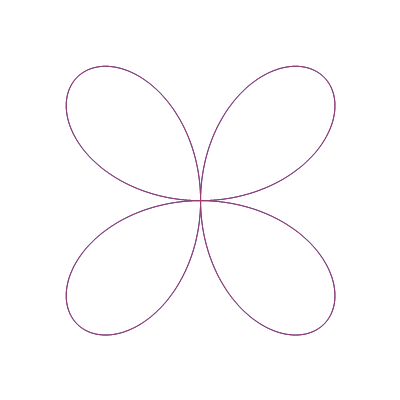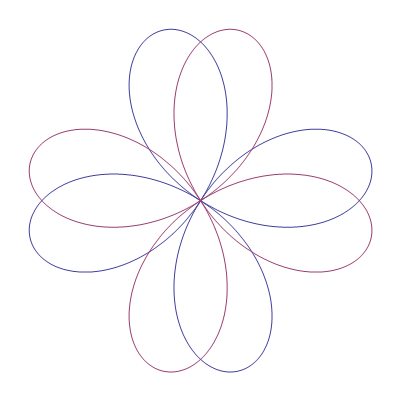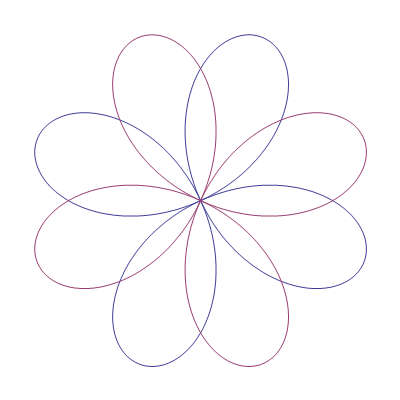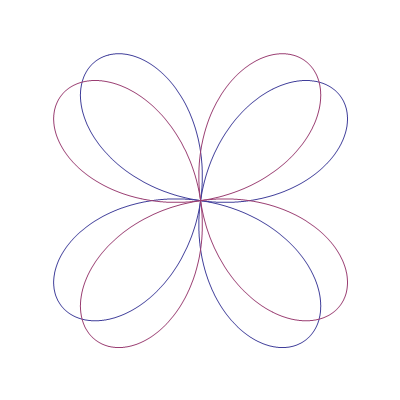
Funkcija ContourPlot
Mathematica funkcija koja omogućuje crtanje implicitno zadanih ravninskih krivulja, tj. skupova točaka čije Kartezijeve koordinate (x,y) zadovoljavaju neku jednadžbu f(x,y)=0, je ContourPlot.
Ova funkcija ima širu namjenu, ali ju možemo koristiti za crtanje implicitno zadanih krivulja na sljedeći način:
Za crtanje jedne krivulje koja je zadana jednadžbom f(x,y)=0, sintaksa je:
ContourPlot[ jednadžba, {x,
,
},{y,
,
}]
Za crtanje više implicitno zadanih krivulja na istom crtežu sintaksa je:
ImplicitPlot [ {
,
,.....} , {x,
,
},{y,
,
}]
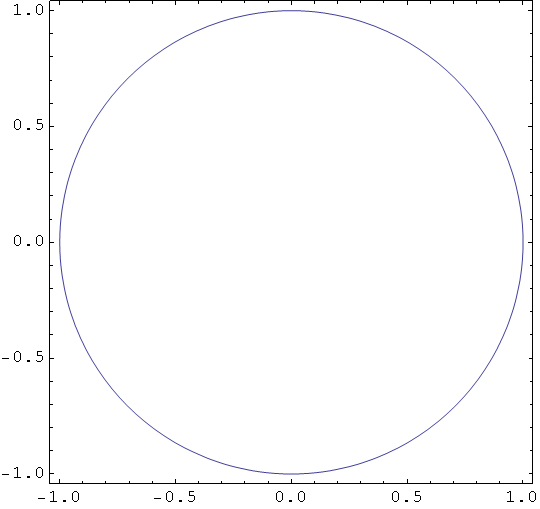
Primjeri 1
In[43]:=
Out[43]=
In[44]:=
Out[44]=
In[45]:=
Out[45]=
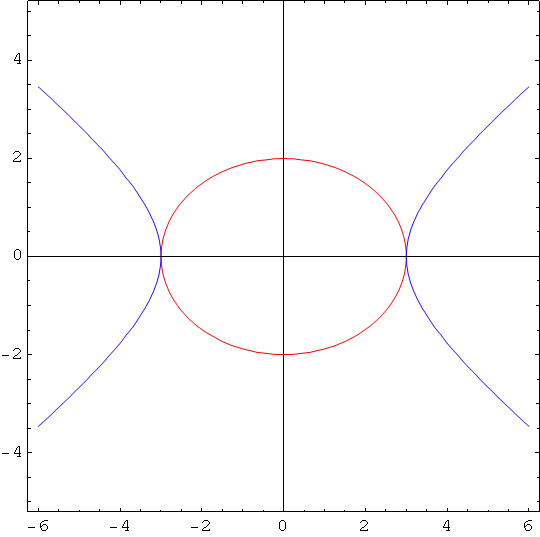
Primjer 2
Cassinijevi ovali.
In[46]:=
In[47]:=
Out[47]=
In[48]:=
Out[48]=
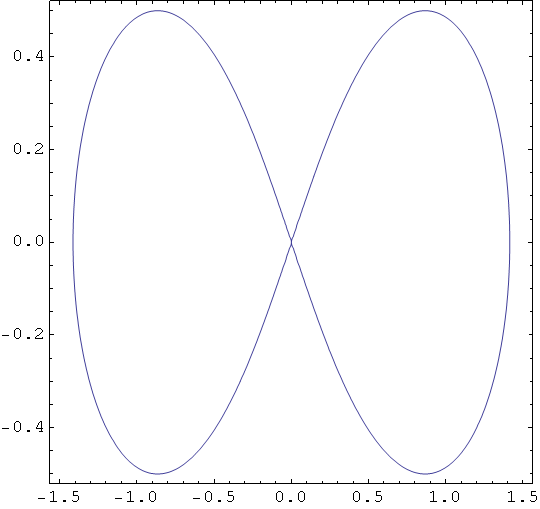
In[49]:=
Out[49]=
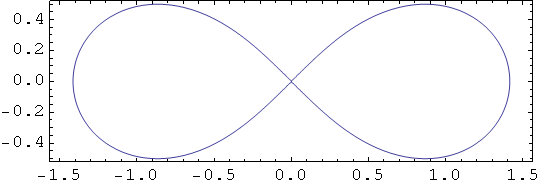
In[50]:=
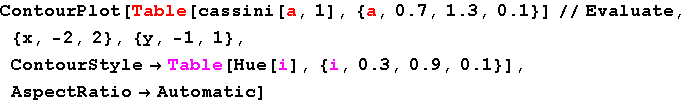
Out[50]=
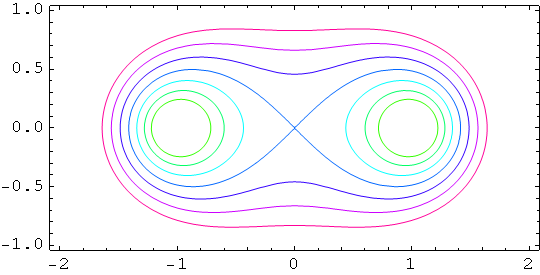
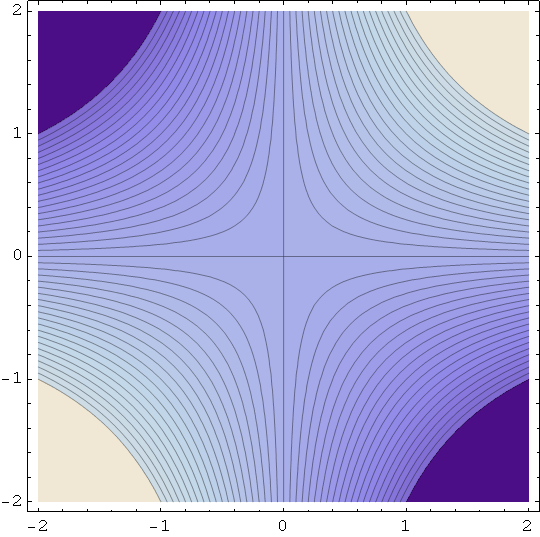
Osnovna namjena funkcije ContourPlot je crtanje nivo linija realne funkcije dviju varijabli z = f (x,y).
Nivo linija je krivulja u ravnini XOY dana jednadžbom f (x,y)=C, gdje je C bilo koji broj koji pripada području vrijednosti funkcije f.
Naredbom:
ContourPlot[ 
, {x,
,
},{y,
,
}]
dobivamo Mathematica prikaz tlocrta plohe z = f (x,y) s istaknutim nivo linijama u području (
,
)×(
,
).
Primjeri
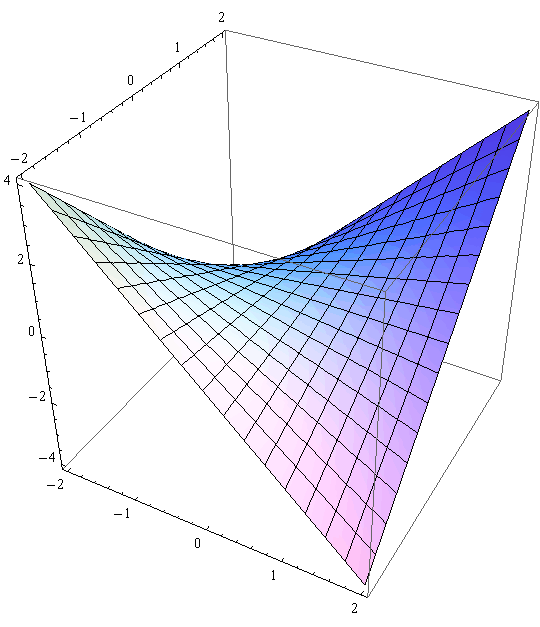
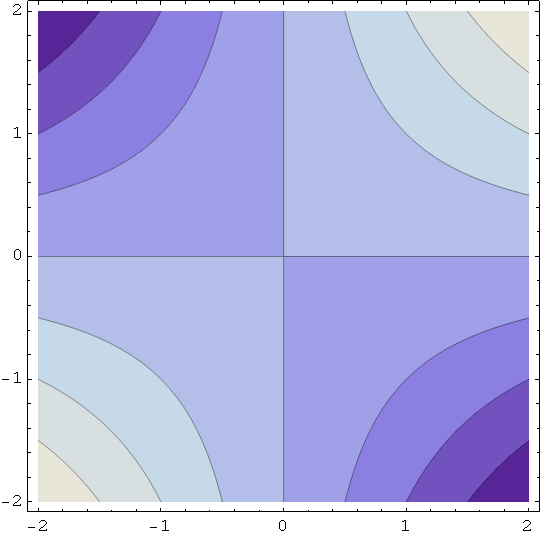
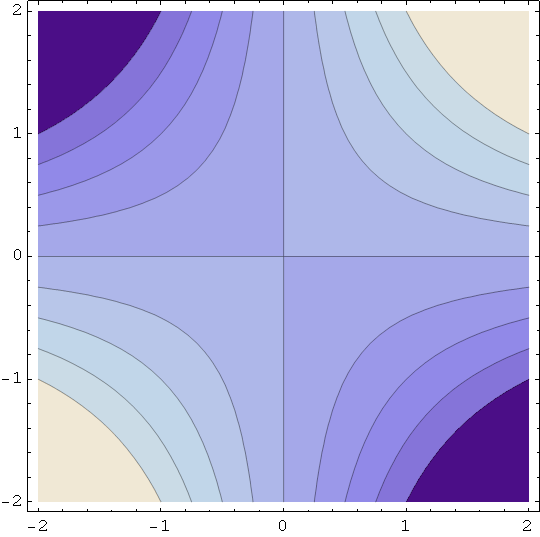
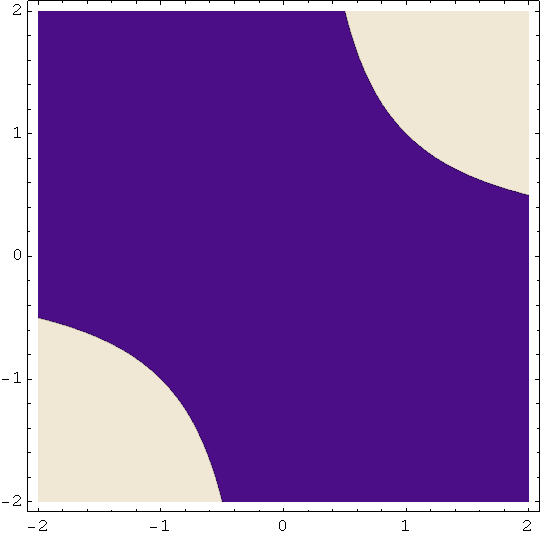
Hiperbolički paraboloid 1 - jednadžba plohe je z = x y
In[51]:=
Out[51]=
In[52]:=
Out[52]=
In[53]:=
Out[53]=
In[54]:=
Out[54]=
In[55]:=
Out[55]=
In[56]:=
Out[56]=
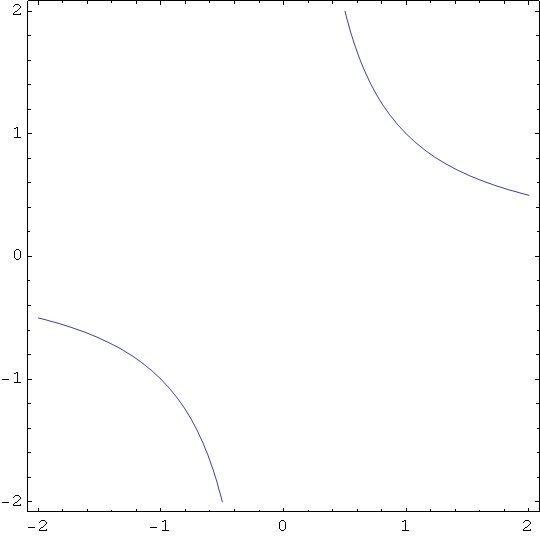
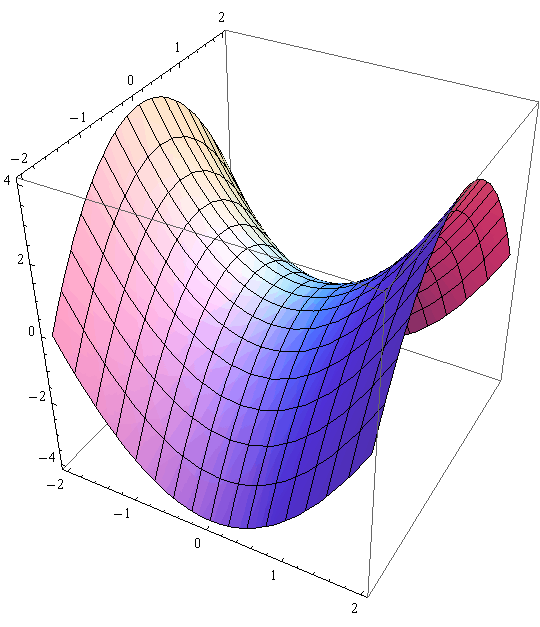
Hiperbolički paraboloid 2 - jednadžba plohe je z = 
- 
In[57]:=
Out[57]=
In[58]:=
Out[58]=
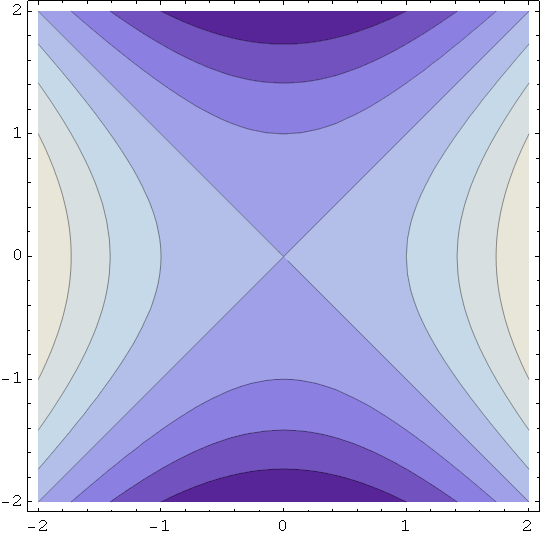
In[59]:=
Out[59]=
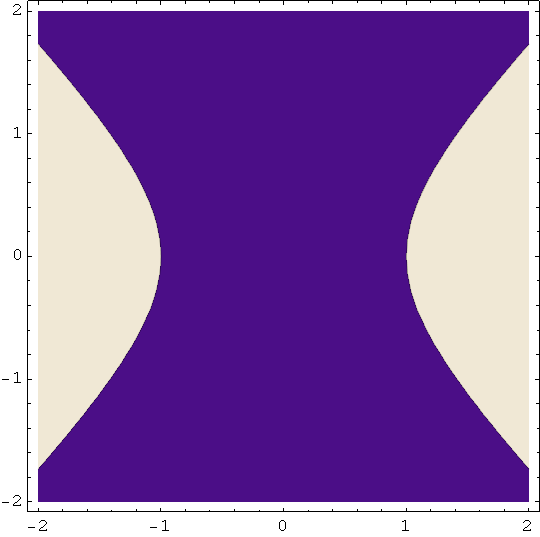
In[60]:=
Out[60]=
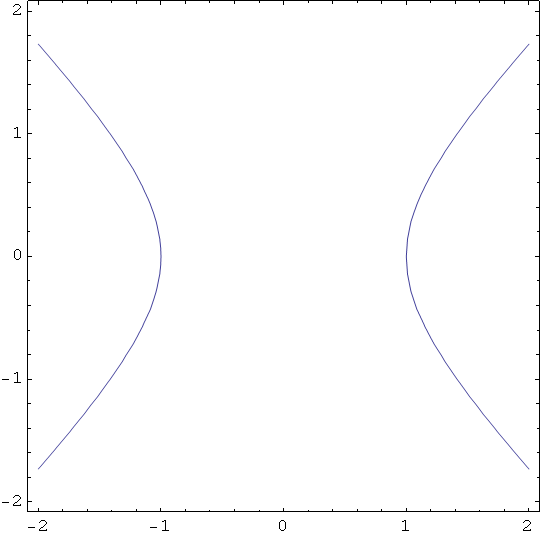
Polukugla
In[61]:=
Out[61]=
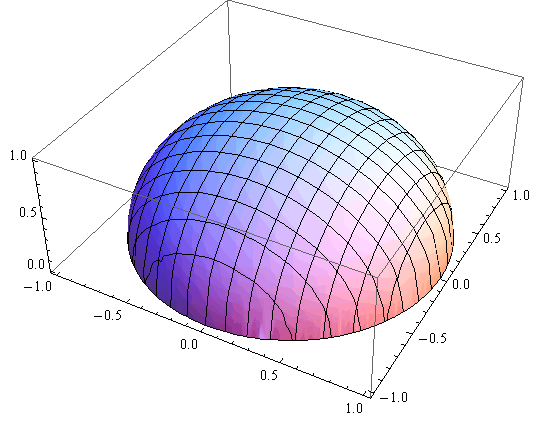
In[62]:=
Out[62]=
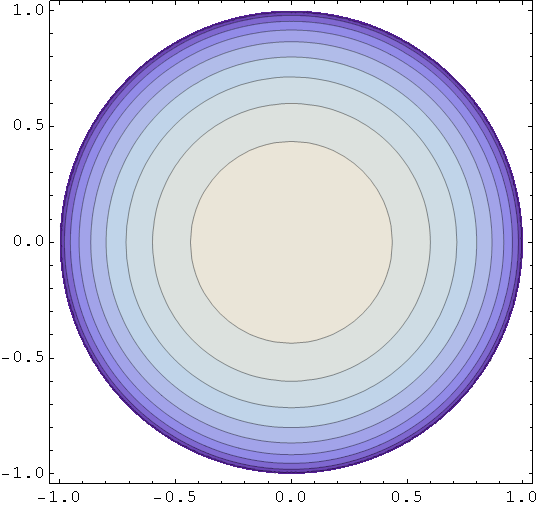
In[63]:=
Out[63]=
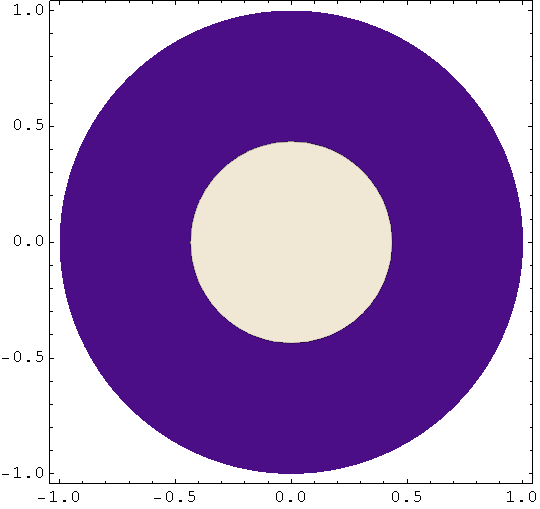
Primjer nealgebarske plohe - jednadžba plohe je z = sinx cosy
In[64]:=
Out[64]=
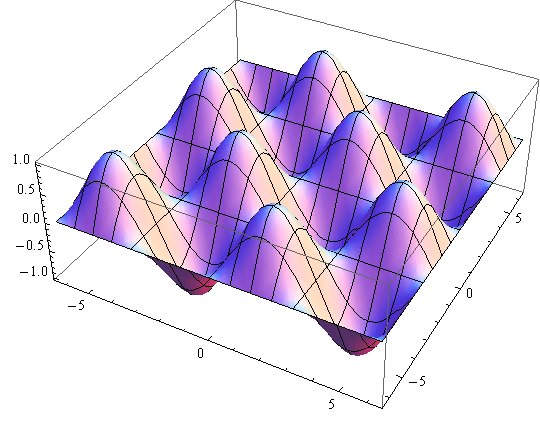
In[65]:=
Out[65]=
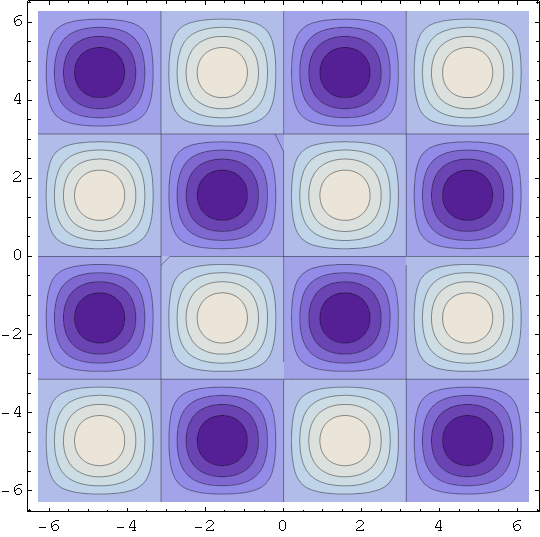
In[66]:=
Out[66]=
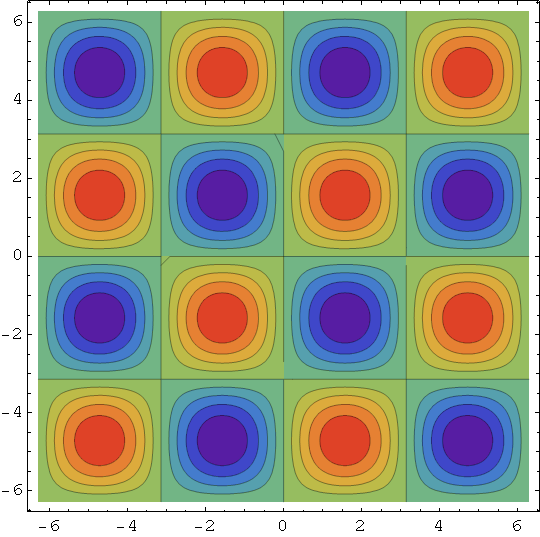
In[67]:=
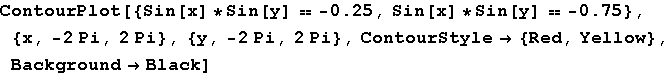
Out[67]=
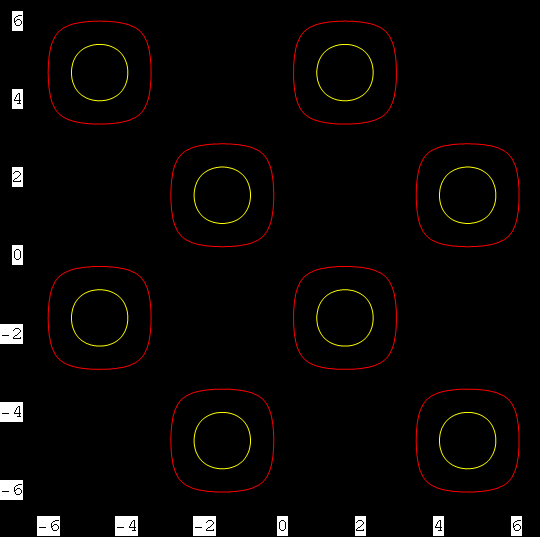
In[68]:=
Out[68]=
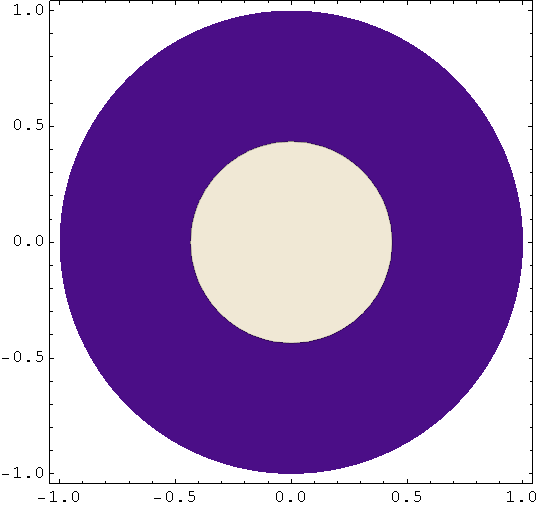
Funkcija RegionPlot
Za grafički prikaz rješenja nejednadžbi koristimo funkciju RegionPlot.
Sintaksa je sljedeća:
RegionPlot[ izraz, {x,
,
},{y,
,
}]
Mathematica prikazuje dio ravnine unutar pravokutnika (
,
)×(
,
) za koji vrijedi izraz.
izraz može biti bilo koja nejednadžba od dvije varijable (x i y) ili logička kombinacija takvih nejednadžbi.
Logički operatori:
ili - ||
i - &&
ne - !
Primjeri
Krug
In[69]:=
Out[69]=
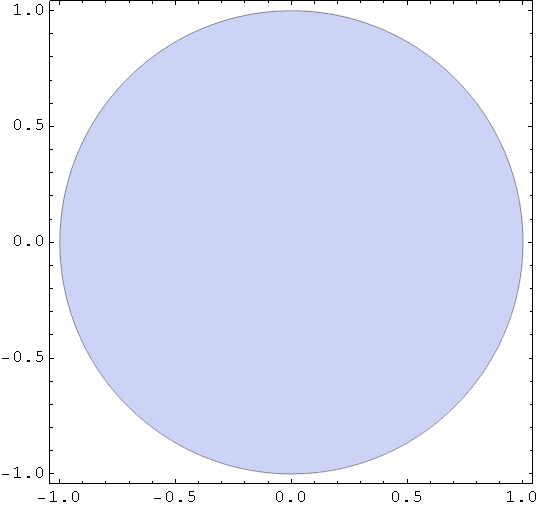
In[70]:=
Out[70]=
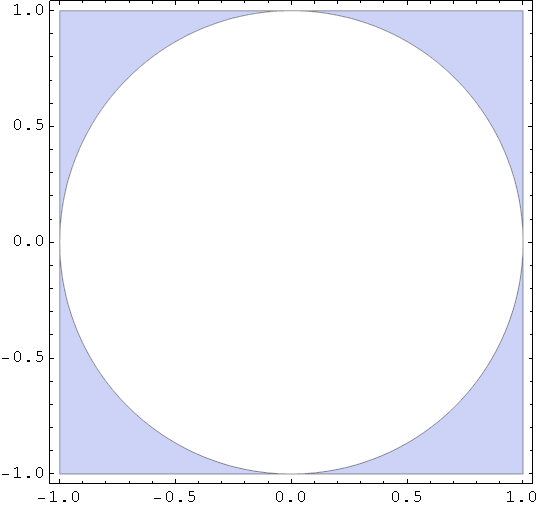
In[71]:=
Out[71]=
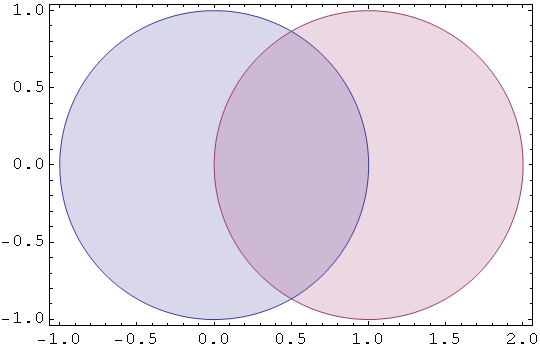
In[72]:=
Out[72]=
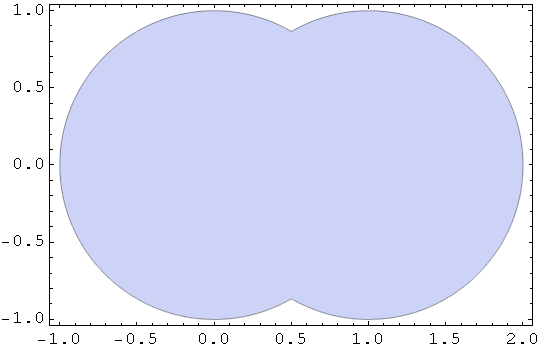
In[73]:=
Out[73]=
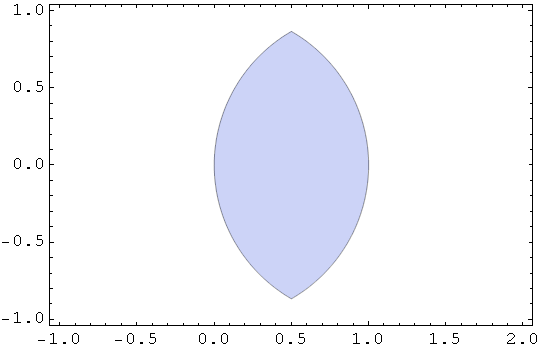
In[74]:=
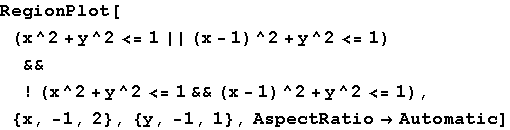
Out[74]=
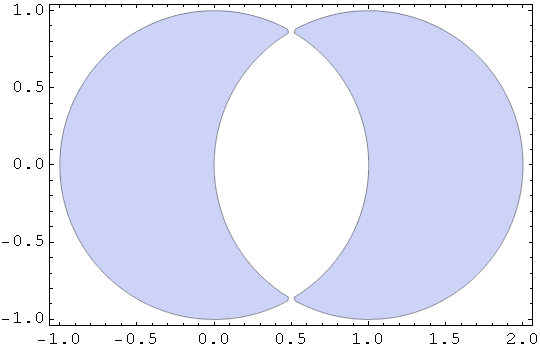
In[75]:=
Out[75]=
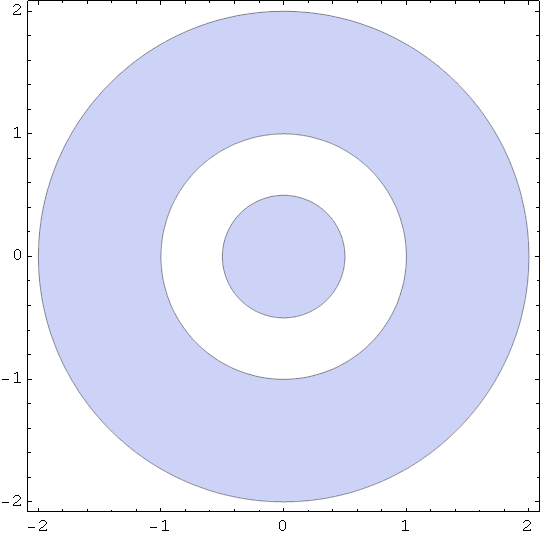
cosx cosy
In[76]:=
Out[76]=
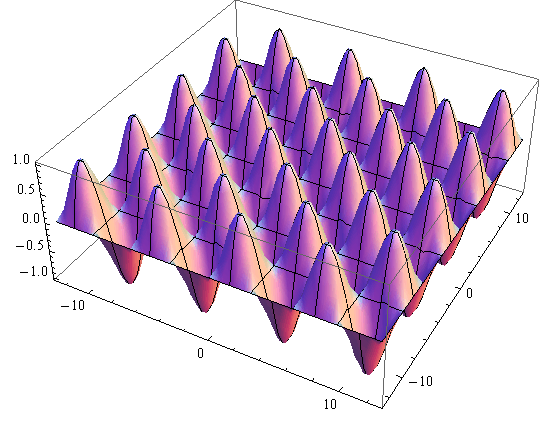
In[77]:=
Out[77]=
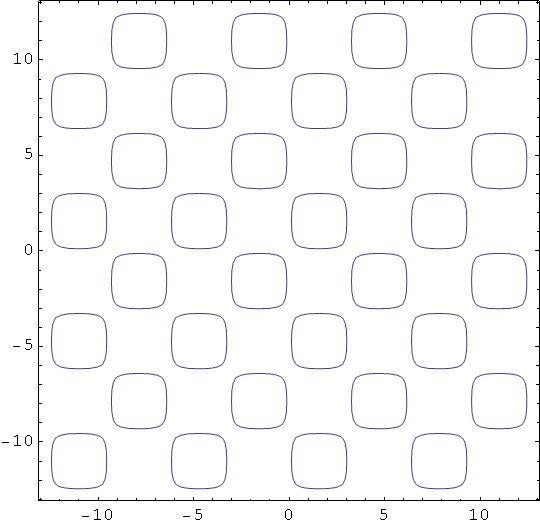
In[78]:=
Out[78]=
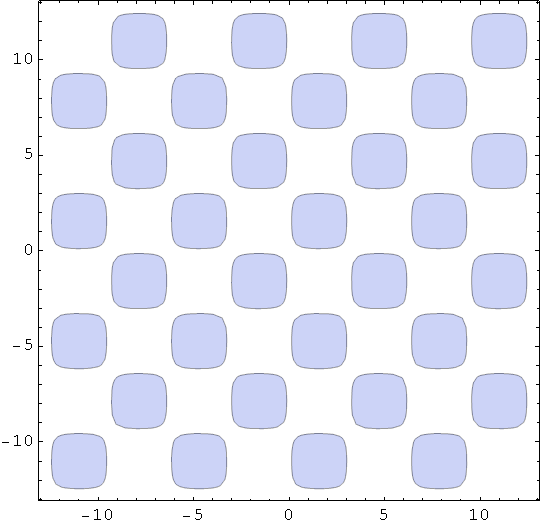
In[79]:=
Out[79]=
Cvjetić
In[80]:=
Out[80]=
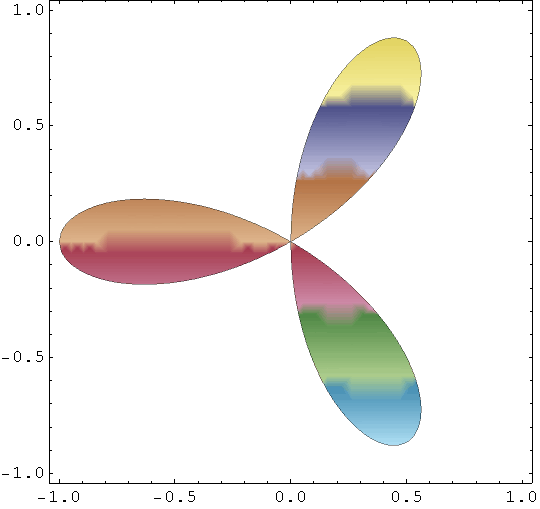
In[81]:=
Out[81]=
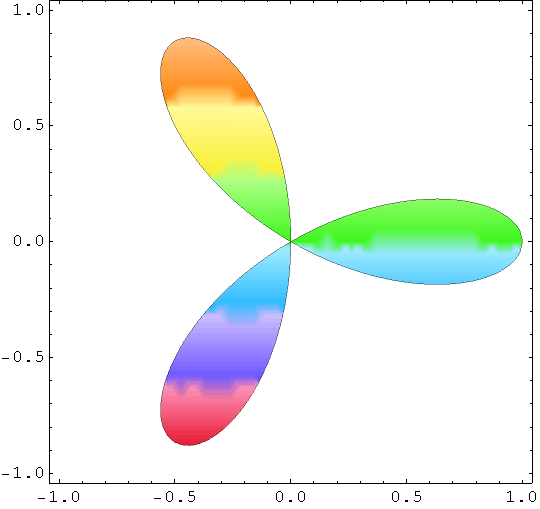
In[82]:=
Out[82]=
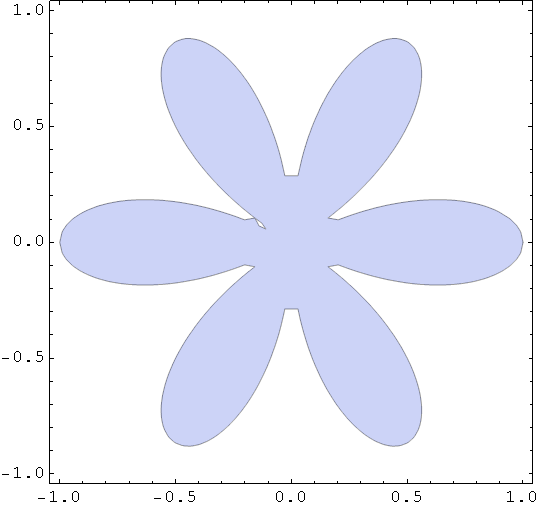
In[83]:=
Out[83]=
Funkcija Show
Show je vrlo važna funkcija u Mathematica grafici, kako za 2D grafiku tako i za 3D grafiku.
Ona omogućuje prikaze većeg broja grafika na istom crtežu (outputu).
Sintaksa je sljedeća:
Show[ grafika, opcije]
ili
Show [
,
,....., opcije]
Opcije navedene u naredbi Show poništavaju one koje su navedene u grafikama.
Primjer
In[84]:=
Out[84]=
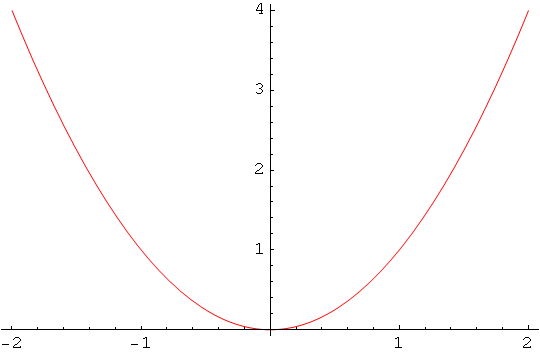
In[85]:=
Out[85]=
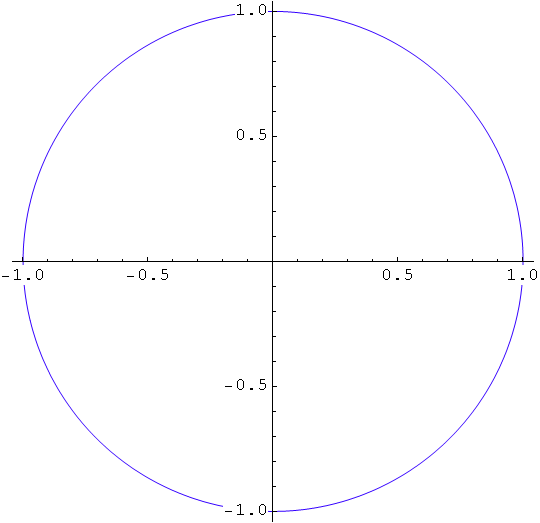
In[86]:=
Out[86]=
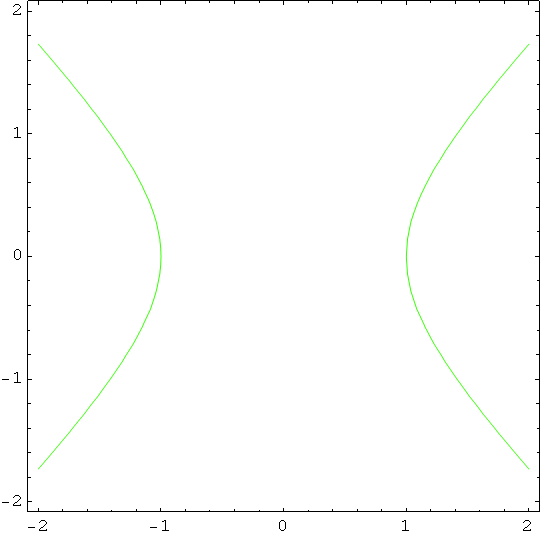
In[87]:=
Out[87]=
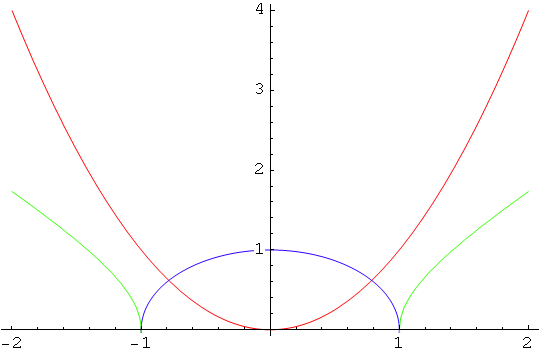
Mathematica za prikaz koristi opcije prve grafike, tj. na gornjem crtežu AspectRatio i PlotRange su oni koje koristi naredba Plot u g1.
Promijenimo li redoslijed grafika, neka je prva grafika g3 ili g2, Show će koristiti drukčije opcije.
In[88]:=
Out[88]=
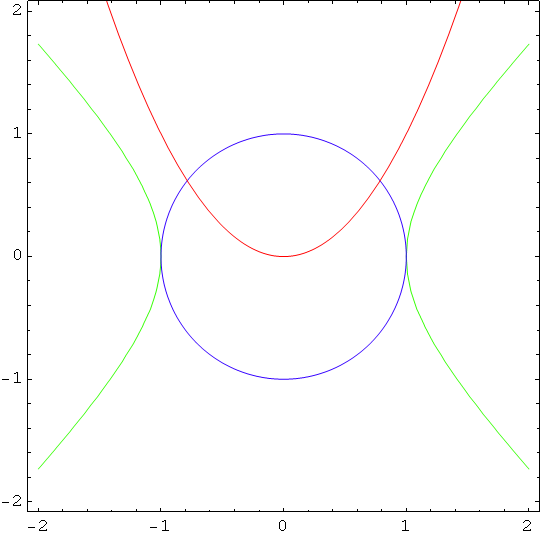
In[89]:=
Out[89]=
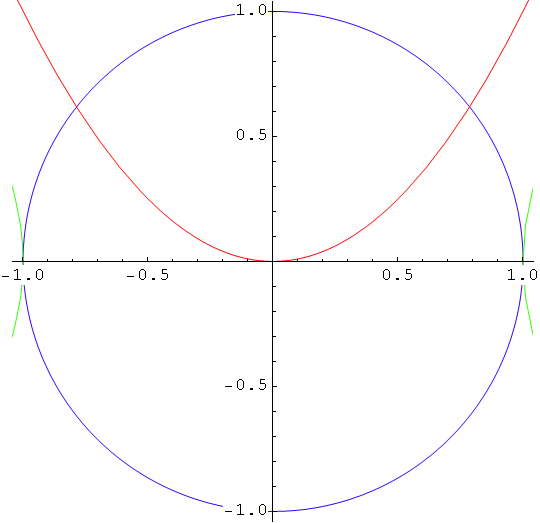
In[90]:=
Out[90]=
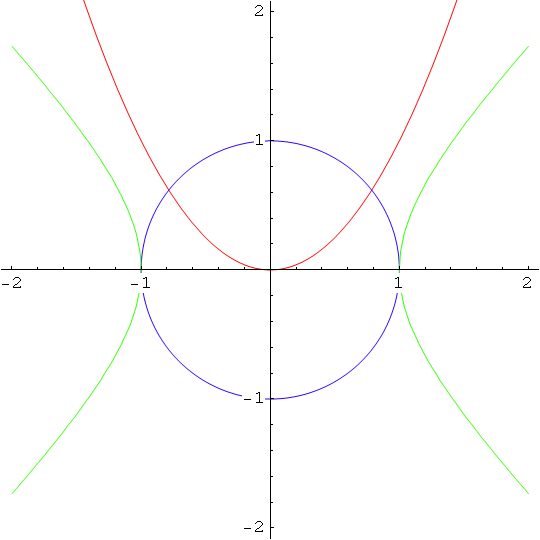
Zadatak
1.) Nacrtajte graf funkcije f(x)=x+sin(
+5) nad intervalom (1,4), crvenom bojom istaknite na njemu točku za koju je x=2.7 te u toj točki nacrtajte tangentu na graf funkcije.
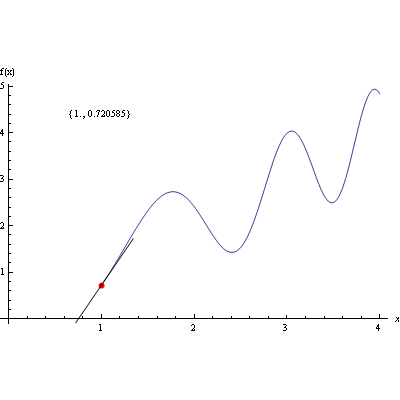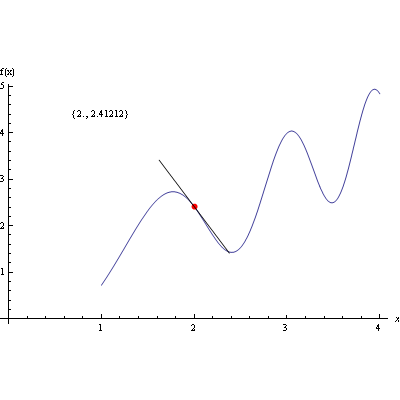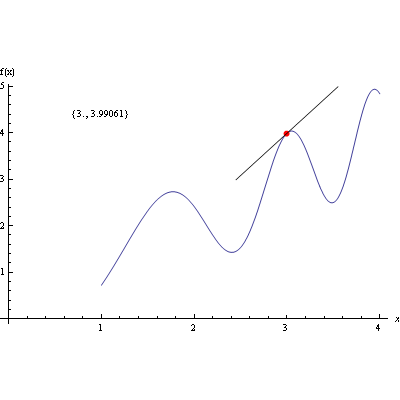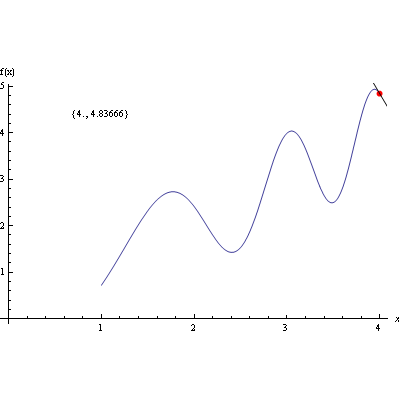
2.) Pomoću funkcije Manipulate prikažite kako se mijenja položaj tangente kada se točka giba po grafu.
In[91]:=
In[92]:=
Out[92]=
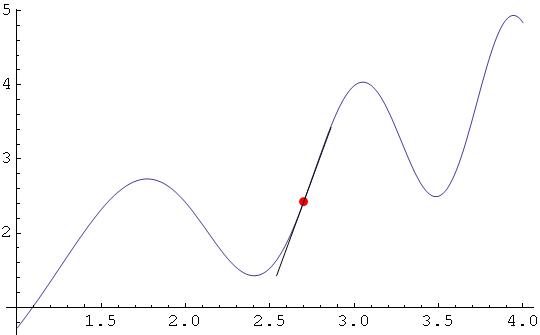
In[93]:=
Out[93]=
Notebook izradili: Sonja Gorjanc, Vladimir Benić
