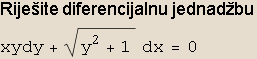Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
6. predavanje
Integrali i diferencijalne jednadžbe
Integrali
Mathematica računa gotovo svaki integral čiji se rezultat prikazuje pomoću elementarnih matematičkih funkcija.
Treba, međutim, imati na umu da postoji puno slučajeva da integral funkcije, koja sadrži samo jednostavne funkcije, može biti vrlo kompliciran ili se uopće ne može izraziti pomoću elementarnih funkcija.
Integrali se računaju pomoću Mathematica funkcija Integrate i NIntegrate.
Ako je f funkcija jedne varijable (npr. x) sintaksa je sljedeća:
Integrate[ f, x] računa neodređeni integral ∫f(x)dx.
Integrate[ f,{x,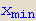 ,
, }] računa određeni integral
}] računa određeni integral 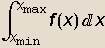 .
.
NIntegrate[ f,{x,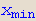 ,
, }] daje numeričku aproksimaciju od
}] daje numeričku aproksimaciju od 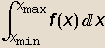 .
.
Pri tome 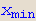 i
i  mogu poprimiti vrijednosti – ∞ i +∞, tj. Mathematica računa i neprave integrale.
mogu poprimiti vrijednosti – ∞ i +∞, tj. Mathematica računa i neprave integrale.
Napomena:
Kod računanja neodređenog integrala Mathematica rezultatu integracije NE DODAJE uobičajenu konstantu C.
Primjeri 1
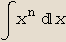
In[1]:=
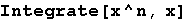
Out[1]=
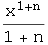
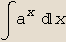
In[2]:=
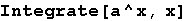
Out[2]=

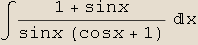
In[3]:=
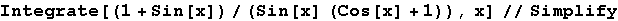
Out[3]=
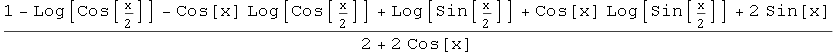
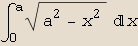
In[4]:=
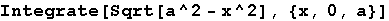
Out[4]=
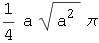
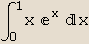
In[5]:=
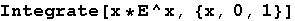
Out[5]=
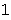
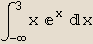
In[6]:=
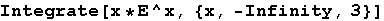
Out[6]=
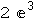
In[7]:=
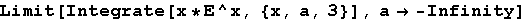
Out[7]=
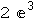
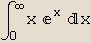
In[8]:=
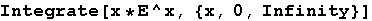
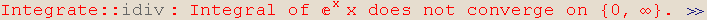
Out[8]=
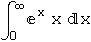
In[9]:=
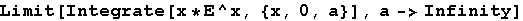
Out[9]=
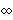
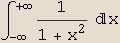
In[10]:=
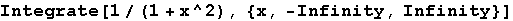
Out[10]=
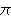
In[11]:=
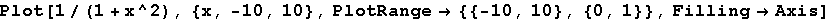
Out[11]=
Primjeri 2
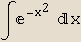
In[12]:=
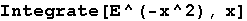
Out[12]=
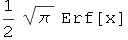
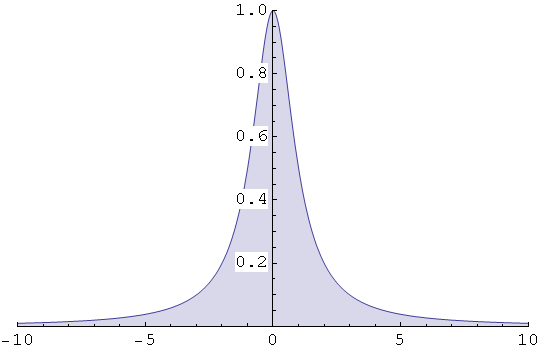
Ovaj integral uključuje funkciju Erf (Error function), koja nije elementarna.
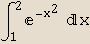
In[13]:=
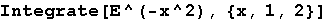
Out[13]=
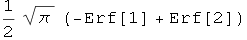
In[14]:=
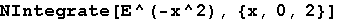
Out[14]=
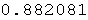
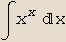
In[15]:=
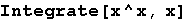
Out[15]=
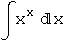
Ovaj se integral ne može opisati pomoću matematičkih funkcija koje koristi Mathematica.
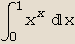
In[16]:=
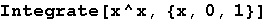
Out[16]=
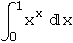
In[17]:=
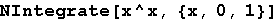
Out[17]=
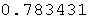
ZADATAK 1
Podsjetite se:
Ako je neprekidna krivulja, u pravokutnim koordinatama, zadana jednadžbom
y = f(x) i ako je na segmentu [a,b] f(x)≥0 (ili f(x)≤0) ,
tada je površina krivocrtnog trapeza omeđenog tom krivuljom, dvjema vertikalama u točkama x=a i x=b te odsječkom na osi apscisa a≤x≤b jednaka
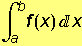 (
(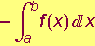 ).
).
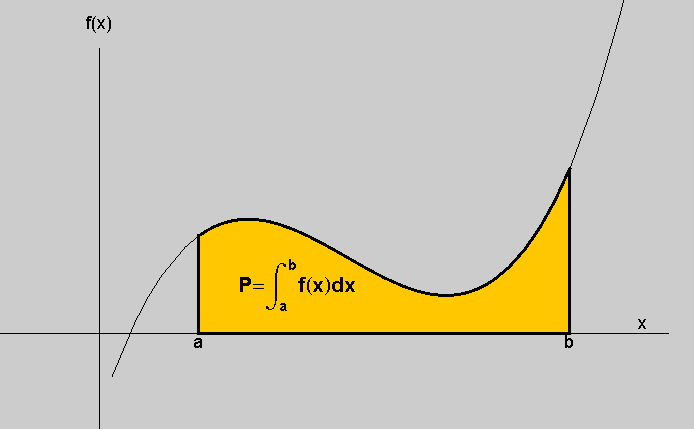
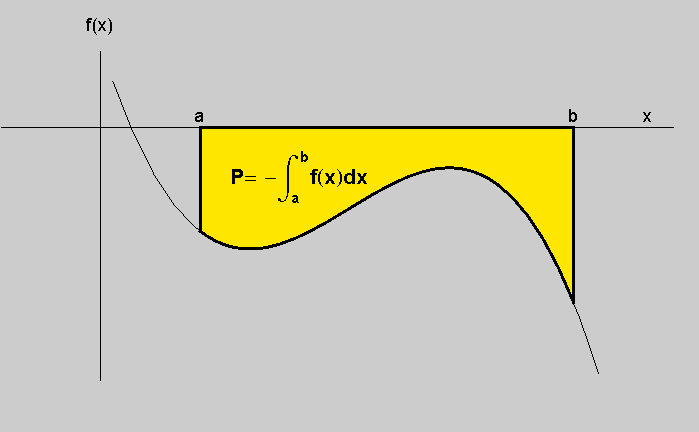
Izračunajte površinu dijela ravnine omeđenog krivuljama sinx i 2sinx nad segmentom [0,2π].
In[18]:=
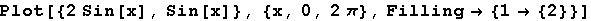
Out[18]=
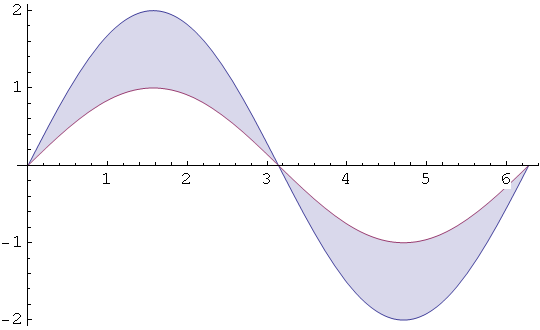
In[19]:=
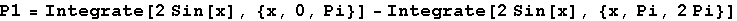
Out[19]=
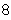
In[20]:=
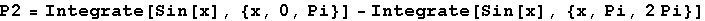
Out[20]=
In[21]:=
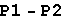
Out[21]=
ZADATAK 2
Podsjetite se:
Volumeni rotacijskih tijela nastalih rotacijom krivocrtnog trapeza omeđenog krivuljom y = f(x), osi x i dvjema vertikalama x=a i x=b, oko osi x ili y određeni su formulama:
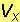 = π
= π 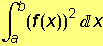 i
i 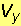 = 2π
= 2π 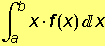 .
.
Izračunajte volumen rotacijskog tijela koje nastaje rotacijom zatvorenog dijela ravnine omeđenog koordinatnim osima i grafom funkcije
f(x)= –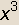 +3
+3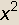 –3x+2, ako je os rotacije:
–3x+2, ako je os rotacije:
1. os y,
2. os x.
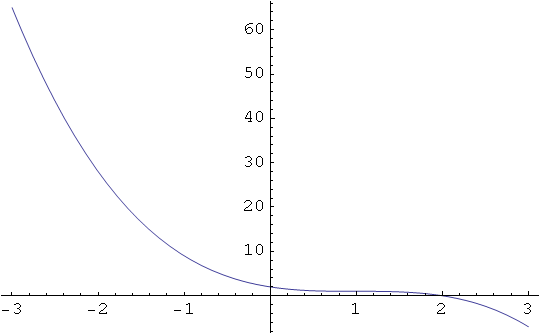
a) Nacrtajmo graf funkcije f(x) nad intervalom [-3,3] i odredimo dio ravnine čijom rotacijom nastaju tijela.
In[22]:=
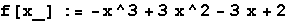
In[23]:=
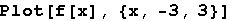
Out[23]=
In[24]:=
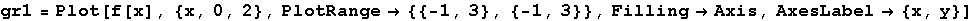
Out[24]=
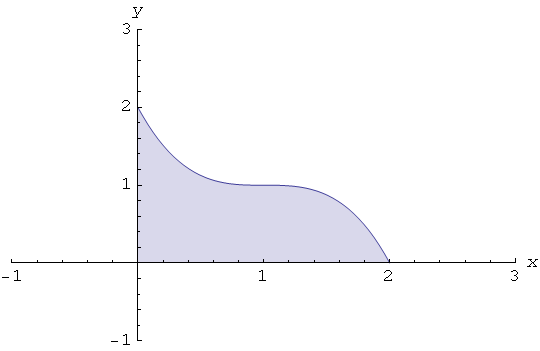
b) Pomoću funkcije RevolutionPlot3D prikažimo tijela koja nastaju rotacijom:
1. oko osi y
In[25]:=
gr2=RevolutionPlot3D[f[t], {t, 0, 2}]
Out[25]=
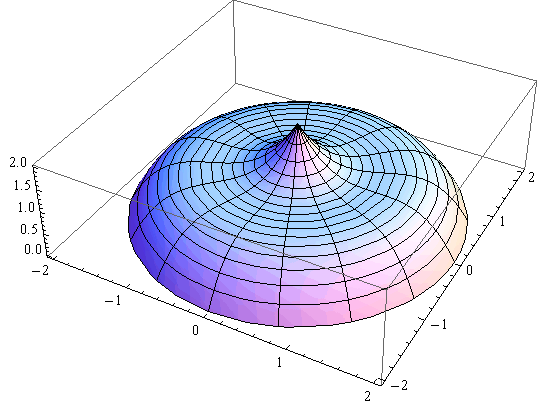
2. oko osi x
In[26]:=
gr3=RevolutionPlot3D[{f[t],t}, {t, 0, 2},ViewVertical->{-1,0,0}]
Out[26]=
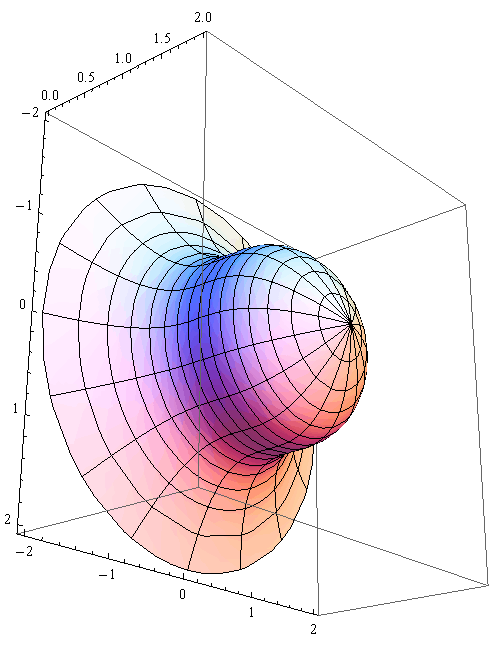
In[27]:=
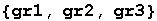
Out[27]=
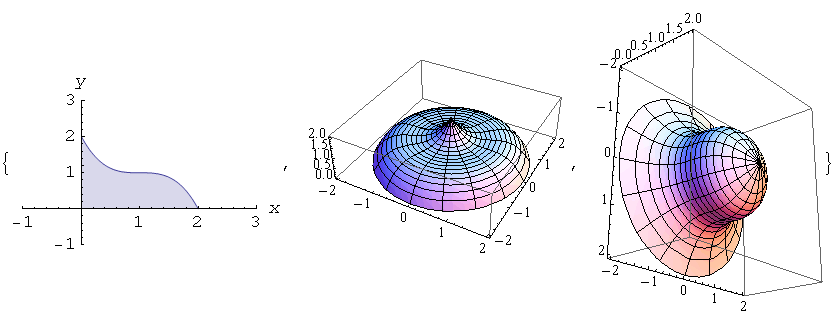
c) Izračunajmo točne i približne vrijednost volumena rotacijskih tijela.
1. os y
In[28]:=
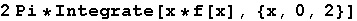
Out[28]=
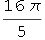
In[29]:=
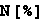
Out[29]=
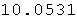
2. os x
In[30]:=
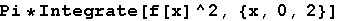
Out[30]=
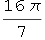
In[31]:=
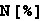
Out[31]=
Diferencijalne jednadžbe
Za razliku od algebarskih jednadžbi, koje su jednadžbe za varijable, diferencijalne jednadžbe su jednadžbe za funkcije. Stoga prilikom zadavanja diferencijalne jednadžbe u programu Mathematica uvijek moramo eksplicitno označavati funkciju (npr. y[x]) i specificirati varijablu (npr. x) o kojoj ta funkcija ovisi.
DSolve[dif.jednadžba, y[x], x]
Daje rješenja dif.jednadžbe za funkciju y[x], uzimajući x kao nezavisnu varijablu.
DSolve[{dif.jednadžba, početni uvjeti}, y[x], x]
Daje rješenja dif.jednadžbe uz početne uvjete za funkciju y[x], uzimajući x kao nezavisnu varijablu.
DSolve[dif.jednadžba, y, x]
Daje rješenja dif.jednadžbe za y u obliku čiste funkcije.
Primjeri 1

In[32]:=
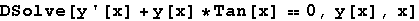
Out[32]=
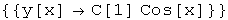
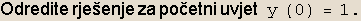
In[33]:=
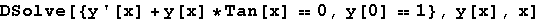
Out[33]=
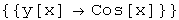
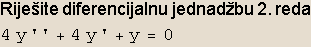
In[34]:=
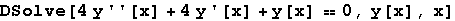
Out[34]=
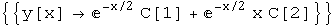

In[35]:=
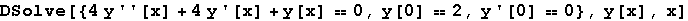
Out[35]=
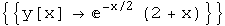
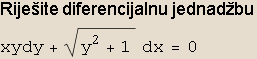
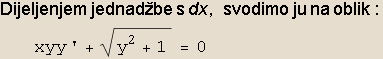
In[36]:=
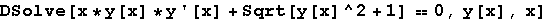
Out[36]=
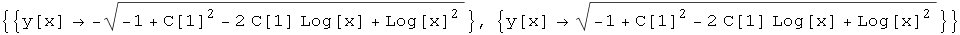
Primjer 2
Isto kao i kod algebarskih jednadžbi, Mathematica ispisuje rješenje u obliku pravila za supstituciju. Npr. za jednadžbu y' = 1 -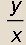 to izgleda ovako:
to izgleda ovako:
In[37]:=
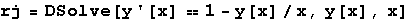
Out[37]=
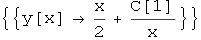
Dakle, s operatorom zamjene /. možemo Mathematici dati naredbu da u bilo kojem izrazu zamijeni y[x] s gornjom vrijednosti.
In[38]:=
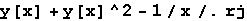
Out[38]=
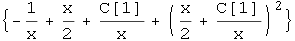
Međutim, to pravilo ne definira zamjenu objekata kao što su npr. y'[x], y''[x].
In[39]:=
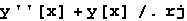
Out[39]=
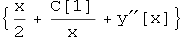
U tim slučajevima, kada želimo manipulirati s rješenjima dobivenim funkcijom DSolve, koristimo ispis rješenja u obliku čiste funkcije tj. nakon upisa jednadžbi NE upisujemo y[x], već samo y.
In[40]:=
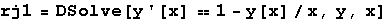
Out[40]=
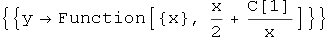
Tada će Mathematica prilikom supstitucije izvršiti i naredbe s kojima djelujemo na funkciju y.
In[41]:=
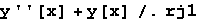
Out[41]=
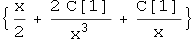
In[42]:=
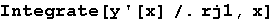
Out[42]=