Jednadžbe u programu Mathematica pišemo tako da između lijeve i desne strane stavimo dva znaka jednakosti ==
Tako na primjer, u programu Mathematica jednadžbu 2
Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
4. predavanje
Jednadžbe, sustavi jednadžbi i nejednadžbe
Rješavanje jednadžbi
Jednadžbe u programu Mathematica pišemo tako da između lijeve i desne strane stavimo dva znaka jednakosti ==
Tako na primjer, u programu Mathematica jednadžbu 2![]() -
- ![]() +
+ ![]() + 3x - 5 = 0 zapisujemo na sljedeći način:
+ 3x - 5 = 0 zapisujemo na sljedeći način:
In[1]:=
![]()
Out[1]=
![]()
U Mathematici postoje 3 funkcije pomoću kojih tražimo rješenja jednadžbi.
1. Naredba Solve -- za rješavanje polinomijanlih jednadžbi stupnja manjeg od 5
Funkciju Solve koristimo za rješavanje jednadžbi sljedećeg oblika:
a![]() +b
+b![]() +c
+c![]() +dx+e = 0
+dx+e = 0
• ako je a≠0 jednadžba je 4. stupnja,
• ako je a=0 i b≠0 jednadžba je 3. stupnja
• itd.
Za ovakve jednadžbe postoje matematičke metode koje daju točna rješenja. One su ugrađene u program.
Mathematica nalazi točna rješenja funkcijom Solve na slijedeći način:
Solve[ jednadžba, nepoznanaica ]
• Solve ispisuje rješenje u obliku liste pravila za supstituciju: { {x → rješenje} }
• Ako postoji više rješenja, Mathematica ispisuje listu pravila za supstitucije: { {x → ![]() },{x →
},{x → ![]() },...}
},...}
Primjer 1
Riješite jednadžbu 2![]() -
- ![]() +
+ ![]() + 3x - 5 = 0.
+ 3x - 5 = 0.
In[2]:=
![]()
Out[2]=
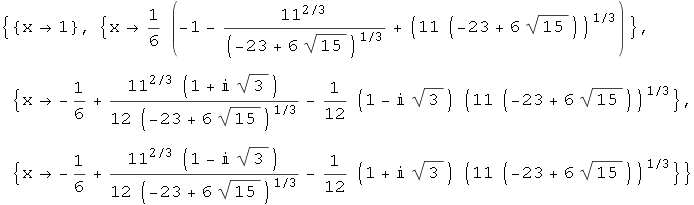
Kao što vidimo rješenja su prikazana točnim izrazima, što ima za posljedicu da su ona vrlo često nepregledna.
Odredimo približne, decimalne vrijednosti:
In[3]:=
![]()
Out[3]=
![]()
Primjer 2 -- formiranje liste rješenja, [ [ ] ]
Riješite jednadžbu ![]() +2
+2 ![]() - 2x - 1 = 0, provjerite da su dobivena rješenja točna i ispišite listu rješenja.
- 2x - 1 = 0, provjerite da su dobivena rješenja točna i ispišite listu rješenja.
In[4]:=
![]()
In[5]:=
![]()
Out[5]=
![]()
Želimo li da Mathematica ispiše pravilo supstitucije za samo jedno rješenje upotrebljavamo oznaku [ [ i ] ], gdje je i redni broj rješenja.
In[6]:=
![]()
Out[6]=
![]()
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
Out[8]=
![]()
In[9]:=
![]()
Out[9]=
![]()
Želimo li da Mathematica ispiše rješenje, a ne pravilo za supstituciju tog rješenja, koristimo - supstituciju varijable x:
In[10]:=
![]()
Out[10]=
![]()
Listu rješenja možemo dobiti pomoću naredbe Table, na sljedeći način:
In[11]:=
![]()
Out[11]=
![]()
2. Naredba NSolve -- za rješavanje polinomijanih jednadžbi bilo kojeg stupnja
Približna rješenja polinomijanle jednadžbe bilo kojeg stupnja dobiti ćemo primjenom funkcije NSolve.
Ovaj način nalaženja rješenja je nužan (za većinu slučajeva) ako je stupanj jednadžbe veći od 4.
Oblik poziva te funkcije je analogan pozivu funkcije Solve:
NSolve[ jednadžba, varijabla]
Rezultati se, kao i kod funkcije Solve, ispisuju u obliku pravila supstitucije.
Primjer
Odredite sva rješenja za nultočke polinoma ![]() + 4
+ 4![]() - 3.
- 3.
Za jednostavniji pregled proslijedite listu rješenja funkciji TableForm.
In[12]:=
![]()
Out[12]=
![]()
In[13]:=
![]()
Out[13]//TableForm=
| x→-1.05278 |
| x→-1. |
| x→-0.391046-1.34313 i |
| x→-0.391046+1.34313 i |
| x→0.826968 |
| x→1.00395-0.867728 i |
| x→1.00395+0.867728 i |
3. Naredba FindRoot -- za rješavanje proizvoljnih jednadžbi
Za proizvoljno zadanu jednadžbu NE postoji postupak dobivanja točnog rješenja nego se moramo zadovoljiti samo približnim rješenjima.
Funkcija koja, u programu Mathematica, pronalazi rješenja proizvoljne jednadžbe je FindRoot.
Za poziv ove funkcije potrebno je poznavati neku točku na x osi koja je blizu traženog rješenja, tj.
potrebno je poznavati grubu aproksimaciju rješenja.
Mathematica, pozivom ove funkcije pronalazi samo jedno rješenje (naravno, ako postoji). Oblik poziva je
FindRoot[ jednadžba ,{varijabla, apriksimacija rješenja}]
Grubu apriksimaciju rješenja, potrebnu za primjenu gornje funkcije, mora se naći na neki drugi način.
Ponekad pretpostavljamo gdje bi moglo biti točno rješenje, no najčešće se traženi podatak očita iz grafa.
Primjer
Odredite pozitivno rješenje jednadžbe cos(x) - ![]() = 0.
= 0.
Uputa:
Nacrtajte graf funkcije f(x)=cos(x) - ![]() npr. na segmentu [-8, 8] i sa slike očitajte približnu vrijednost pozitivne nultočke. Ako je segmet prevelik za očitavanje nacrtajte graf na manjem segmentu i očitajte približno rješenja. Zatim primjenite funkciju FindRoot.
npr. na segmentu [-8, 8] i sa slike očitajte približnu vrijednost pozitivne nultočke. Ako je segmet prevelik za očitavanje nacrtajte graf na manjem segmentu i očitajte približno rješenja. Zatim primjenite funkciju FindRoot.
In[14]:=
![]()
Out[14]=
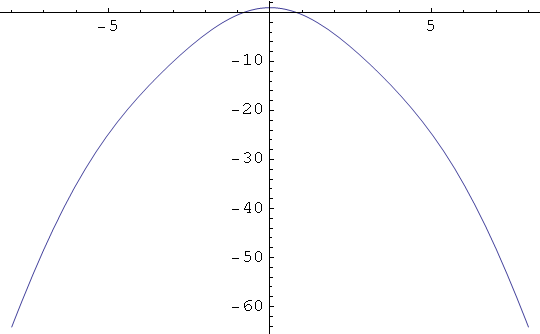
Sa slike se nazire da funkcija ima dvije nultočke. Da bi odredili aproksimaciju pozitivne nultočke nacrtajmo graf na segmentu [0, 1.5].
In[15]:=
![]()
Out[15]=
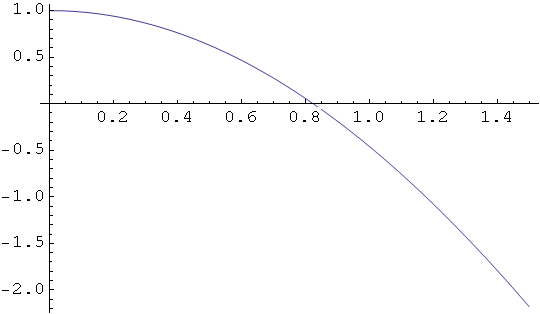
Za aprokcimaciju ćemo uzeti x=0.8. Primjenimo sada FindRoot da dobijemo rješenje.
In[16]:=
![]()
Out[16]=
![]()
Napomena: da smo kao aproksimativno rješenje uzeli negativan broj, npr. x= -0.1 dobili bismo negativno rješenje. Zaista:
In[17]:=
![]()
Out[17]=
![]()
Rješavanje sustava linearnih jednadžbi
Rješenje sustava linearnih jednadžbi dobiti ćemo funkcijom Solve. Ovu funkciju smo već upoznali pri rješavanju polinomijalnih jedadžbi do uključivo 4. stupnja. Poziv funkcije Solve pri rješavanju linearnih sustava je nešto drukčiji i glasi:
Solve[ lista linearnih jednadžbi ]
• Ako sustav ima jedinstveno rješenje, funkcija Solve će ispisati listu pravila supstitucije za to rješenje.
• Ako sustav nema rješenja, bit će ispisana lista bez elemenata tj. bit će ispisana lista { }.
• Ako sustav ima beskonačno mnogo rješenja, bit će ispisana lista parametarskih rješenja.
Primjer 1
Odredite rješenje sustava
3x + y + 2z = 5
x + 2y + 3z = 7
4x + y + 5 z= 4
In[18]:=
![]()
Out[18]=
![]()
Vidimo da sustav ima jedinstveno rješenje. Decimalni prikaz rješenja je
In[19]:=
![]()
Out[19]=
![]()
Primjer 2
Odredite rješenje sustava
3x + y + 2z = 0
x + 2y + 3z = 7
4x + 3y + 5z = 5
In[20]:=
![]()
Out[20]=
![]()
Znači, sustav nema rješenja.
Primjer 3
Odredite rješenje sustava
3x + y + 2z = 0
x + 2y + 3z = 7
4x + 3y + 5z = 7
In[21]:=
![]()
![]()
Out[21]=
![]()
Iz gornjeg slijedi da sustav ima beskonačno mnogo rješenja, pri čemu je kao parametar izabrana varijabla z.
Drugim riječima varijabla z može biti bilo koji realan broj dok se, tada, odgovarajući x i y računaju po gornjim formulma.
Napomena: gornja primjedba programa Mathematica, prikazana crvenim slovima, posljedica je činjenice da Mathematica ne može prikazati formulu za vrijednost varijable z budući da je z proizvoljan.
Primjer 4 -- nelinearne jednadžbe
Odredite rješenja sustava
3![]() +
+ ![]() + 2z = 5
+ 2z = 5![]() + 2y + 3z = 7
+ 2y + 3z = 7
4x + y + 5 z= 4
In[22]:=
![]()
Out[22]=
In[23]:=
![]()
Out[23]=
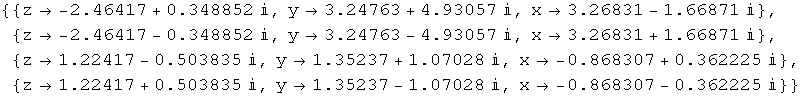
In[24]:=
![]()
Out[24]//TableForm=
| z→-2.46417+0.348852 i | y→3.24763+4.93057 i | x→3.26831-1.66871 i |
| z→-2.46417-0.348852 i | y→3.24763-4.93057 i | x→3.26831+1.66871 i |
| z→1.22417-0.503835 i | y→1.35237+1.07028 i | x→-0.868307+0.362225 i |
| z→1.22417+0.503835 i | y→1.35237-1.07028 i | x→-0.868307-0.362225 i |
Rješavanje nejednadžbi
Nejednadžbe Mathematica shvaća kao logičke izraze koji su istiniti za neke vrijednosti realne varijable x, a neistiniti za neke druge vrijednosti (varijabla se, naravno, ne mora zvati x).
Funkcija koja reducira (pojednostavljuje) logičke relacije na jednostavnije i time omogućava da jednostavno očitamo rješenja nejednadžbi zove se Reduce.
Poziv funkcije je:
Reduce[ nejednadžba, varijabla ]
ili, ako želimo riješiti sustav nejednadžbi
Reduce[ lista nejednadžbi, varijabla ]
Rezultat se, najčešće, prikazuje pomoću nekoliko podintervala ili jednakosti.
Između njih stoje zankovi || ili && koji se čitaju na sljedeći način:
• niz znakova || se čita ili
• niz znakova && se čita i.
Na primjer, izraz 1<x<3 || 4<x<8 se čita: x je između 1 i 3 ili je x između 4 i 8.
Primjer 1
Riješite nejednadžbu ![]() - 5x + 6 > 0.
- 5x + 6 > 0.
In[25]:=
![]()
Out[25]=
![]()
Rješenje: x je manje od 2 ili veće od 3, tj. xε(-∞,2)∪(3,∞)
Primjer 2
Riješite nejednadžbu ![]() - 5x + 6 > 0.
- 5x + 6 > 0.
In[26]:=
![]()
Out[26]=
![]()
Rješenje: nejednadžba vrijedi za sve relane x, tj. xεR
Primjer 3
Riješite nejednadžbu ![]() - 5x + 6 < 0.
- 5x + 6 < 0.
In[27]:=
![]()
Out[27]=
![]()
Rješenje: nejednadžba ne vrijedi niti za jedan realni x, tj. skup rješenja je φ.
Primjer 4
Riješite sustav nejednadžbi![]() -
- ![]() -32x +60 >0
-32x +60 >0
x - 1 ≥ 0
In[28]:=
![]()
Out[28]=
![]()
Rješenje: x je između 1 i 2 ili je x veći od 5, tj. xε[1,2)∪(5,∞)
Notebook izradili: Sonja Gorjanc, Vladimir Benić