Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
3. predavanje
Algebarsko računanje, definiranje funkcija i njihovi grafovi
Algebarsko računanje
Važno svojstvo Mathematice je to da simbolički računa jednako dobro kao i numerički.
Mi smo već u prethodnim primjerima koristili simboličko računanje (većina primjera u kojima su se pojavljivali simboli a, b, c, x, z, y....)
U Mathematicu je ugrađen velik broj standardnih pravila za transformiranje algebarskih izraza i napišemo li neki algebarski izraz Mathematica će ga automatski "srediti".
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
![]()
Out[2]=
![]()
Ponekad nam čak neće niti odgovarati činjenica što Mathematica ima ugrađene "zaštite" protiv pogrešnog računa.
In[3]:=
![]()
Out[3]=
![]()
Sljedeći primjer prikazuje kako Mathematica "sređuje" izraz ![]() .
.
In[4]:=
![]()
Out[4]=
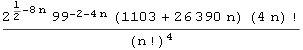
Funkcije Factor, Expand i Simplify
In[5]:=
![]()
Out[5]=
![]()
Želimo li da Mathematica ispiše gornji polinom u razvijenom obliku (izvrši množenja i potenciranja te rezultat napiše u obliku sume) upotrebljavamo funkciju Expand.
In[6]:=
![]()
Out[6]=
![]()
Funkcija Factor prikazuje zadani polinom rastavljen na faktore.
In[7]:=
![]()
Out[7]=
![]()
Koji je oblik algebarskog izraza jednostavniji? Odgovor na to pitanje nije jednoznačan.
Ponekad je jednostavniji razvijeni oblik,
In[8]:=
![]()
Out[8]=
![]()
In[9]:=
![]()
Out[9]=
![]()
a ponekad je jednostavniji faktorizirani.
In[10]:=
![]()
Out[10]=
![]()
Mathematica ima ugrađenu funkciju Simplify, koja često može dobro poslužiti: Mathematica će pregledati moguće oblike i prikazati onaj koji sadrži najmanje dijelova.
In[11]:=
![]()
Out[11]=
![]()
In[12]:=
![]()
Out[12]=
![]()
In[13]:=
![]()
Out[13]=
![]()
In[14]:=
![]()
Out[14]=
![]()
Naredba Factor dozvoljava faktorizaciju samo s cjelobrojnim koeficijentima.
Stoga, iako je poznato da potpuna faktorizacija polinoma s koeficijentima iz skupa realnih brojeva sadrži samo polinome 1. i 2. stupnja, Mathematica nam često neće faktorizirati onako kako bismo željeli. Na primjer:
In[15]:=
![]()
Out[15]=
![]()
ili
In[16]:=
![]()
Out[16]=
![]()
No, ako Mathematicu znamo uputiti gotovo uvijek možemo doći do odgovarajućeg rezultata. Naredbama Factor, Expand i Simplify možemo dodavati neke opcije te ih usmjeravati u nama interesantnom smjeru. Na primjer, opcijom Extension možemo Mathematici dodati popis realnih brojeva za koje želimo da ih uključi pri faktorizaciji. Za gornje primjere to može izgeedati ovako:
In[17]:=
![]()
Out[17]=
![]()
In[18]:=
![]()
Out[18]=
![]()
Ili, primjer koji smo već spomenuli:
In[19]:=
![]()
Out[19]=
![]()
u kojem nam funkcija Simplify, bez dodatnih opcija, neće pomoći.
In[20]:=
![]()
Out[20]=
![]()
Međutim, funkcija Simplify dozvoljava i određivanje matematičkih uvjeta ili pretpostavki. U tom je slučaju sintaksa sljedeća:
● Simplify[algebarski izraz,uvjet]
In[21]:=
![]()
Out[21]=
![]()
In[22]:=
![]()
Out[22]=
![]()
Opcijom Extension i unosom pretpostavke uz narebu Simplify, naveli smo samo dvije od velikog broja dodatnih mogućnosti koje nam Mathematica dozvoljava uz funkcije Factor, Expand i Simplify. Za njihovu obradu, makar i na nivou pobrojavanje, nemamo u okviru našeg kolegija dovoljno prostora. No, ako se nađete u situaciji da vam se Mathematica čini baš "glupom" za zadatak u kojem očekujete njezinu pomoć, pregledajte malo Mathematica Help i najvjerojatnije ćete pronaći način kako da usmjerite rad programa. Ako vam to ne uspije, pregledajte pažljivije, udubite se u primjere....
Pridruživanje vrijednosti simbolima -- znak /.
Želimo li izvršiti supstituciju u nekom matematičkom izrazu, tj. želimo simbole zamijeniti brojevima ili nekim drugim matematičkim izrazima, upotrebljavamo znak /. (sleš-točka, bez razmaka).
In[23]:=
![]()
Out[23]=
![]()
In[24]:=
![]()
Out[24]=
![]()
In[25]:=
![]()
Out[25]=
![]()
In[26]:=
![]()
Out[26]=
![]()
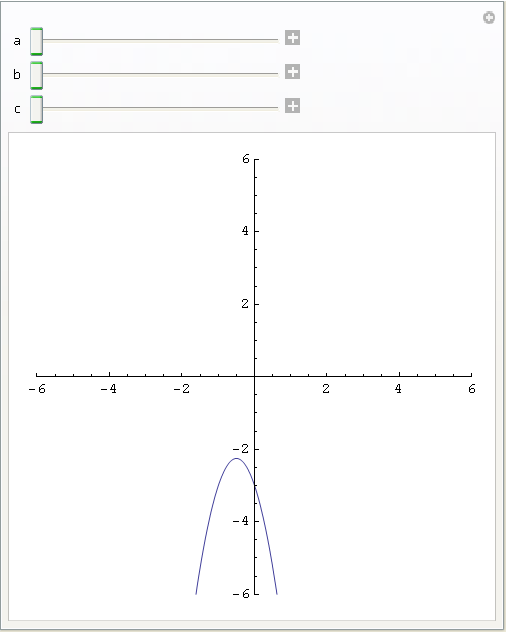
Funkcija Manipulate
Manipulate je nova funkcija u Mathematici 6.
In[27]:=
![]()
In[28]:=
![]()
Out[28]=
Definiranje funkcija
U Mathematicu je ugrađen velik broj funkcija, no korisniku često trebaju funkcije kojih nema u programu Mathematica. Stoga je potrebno poznavati postupak definiranja funkcija.
Na primjer, ako vam treba funkcija f(x)= cos(2·x+1) + ![]() potrebno ju je definirati, jer ona u programu Mathematica nije definirana.
potrebno ju je definirati, jer ona u programu Mathematica nije definirana.
Pretpostavimo da ćemo nezavisnu varijablu zvati x a funkciju f.
Tada je opći oblik formule za zadavanje funkcije f jednak
● f[x_] := formula za funkciju
Na primjer, gornju funkciju zadat ćemo izrazom:
In[29]:=
![]()
Sad možemo računati vrijednost funkcije za bilo koji element iz njezine domene.
In[30]:=
![]()
Out[30]=
![]()
In[31]:=
![]()
Out[31]=
![]()
Ili za neki matematički izraz.
In[32]:=
![]()
Out[32]=
![]()
Možemo tražiti da Mathematica usporedi vrijednosti funkcije za pojedine brojeve.
In[33]:=
![]()
Out[33]=
![]()
In[34]:=
![]()
Out[34]=
![]()
Važno:
f[x_] := formula za funkciju
• Nezavisna varijalba pisana lijevo od := mora završiti znakom _ (underline).
• Lijeva i desna strana definicije funkcije razdvojene su znakovima := a ne samo znakom =.
• Imena funkcija i varijabli su proizvoljna, jedino treba paziti da ne počinju velikim slovom budući da je takav oblik naziva razerviran za funkcije u Mathematici .
• Ime varijable ili funkcije NE SMIJE početi brojem niti smije sadržavati znakove aritmetičkih operacija +, - *, /, ^.
Graf funkcije jedne varijable
Mathematica naredba koja omogućuju crtanje grafa funkcije f : I → R, I⊆R, je Plot, a sintaksa je sljedeća:
● Plot[f(x),{x,![]() ,
,![]() }]
}]
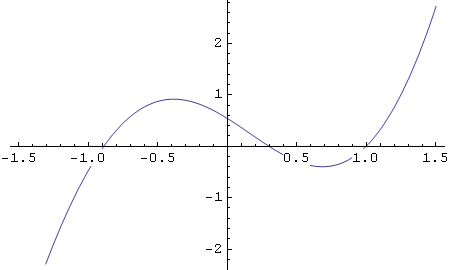
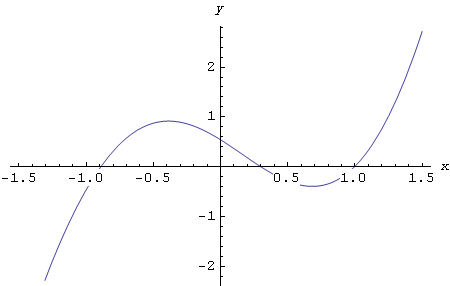
Tako na primjer naredba za crtanje grafa funkcije f(x)= cos(2·x+1) + ![]() , za x∈[-1.5,1.5], izgleda ovako:
, za x∈[-1.5,1.5], izgleda ovako:
In[35]:=
![]()
Out[35]=
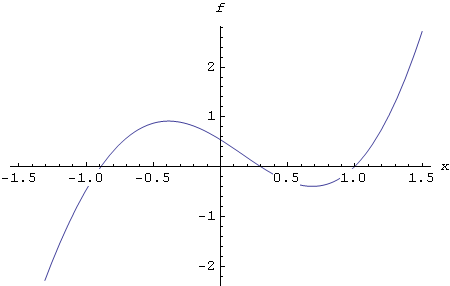
Ili, budući da smo upravo tu funkciju ranije definirali u Mathematici, možemo pisati:
In[36]:=
![]()
Out[36]=
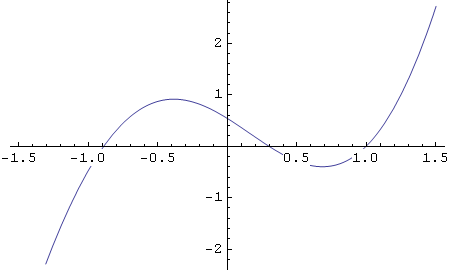
![]()
Kako Mathematica određuje veličine jedinica na osima?
U zadatku smo zadali da je x između -1.5 i 1.5. Mathematica izračuna vrijednost funkcije za izvjestan broj točaka u tom intervalu i među tim vrijednostima nađe minimalnu i maksimalnu. Tada veličinu jedinica na osima x i y određuje tako da budu zadovoljeni sljedeći uvjeti:

Utjecati na izgled slike možemo pomoću opcija koje dodajemo naredbi na sljedeći način:
● Plot[f(x),{x,![]() ,
,![]() },opcija1,opcija2,..]
},opcija1,opcija2,..]
Listu opcija za naredu Plot možemo u Mathematici dobiti na sljedeći način:
In[37]:=
![]()
Out[37]=

Ovdje ćemo spomenuti samo neke od njih.
Opcija AspectRatio
In[38]:=
![]()
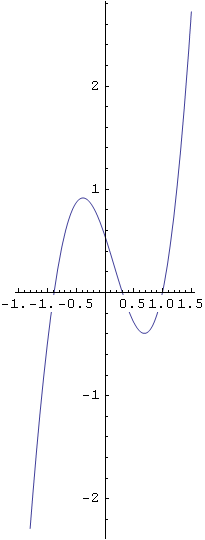
Opcijom AspectRatio izražava se omjer visine i širine slike.
In[39]:=
![]()
Out[39]=
In[40]:=
![]()
Out[40]=
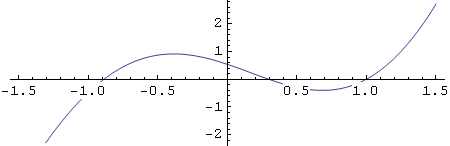
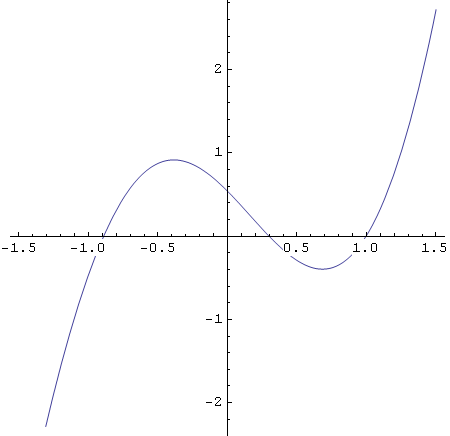
Kvadratni oblik slike -- AspectRatio -> 1
In[41]:=
![]()
Out[41]=
Jednake jedinice na osima -- AspectRatio->Automatic.
In[42]:=
![]()
Out[42]=
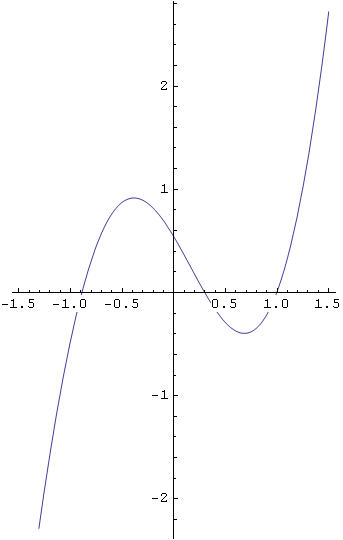
Opcija AxesLabel
Pomoću opcije AxesLabel imenujemo osi.
In[43]:=
![]()
Out[43]=
In[44]:=
![]()
Out[44]=
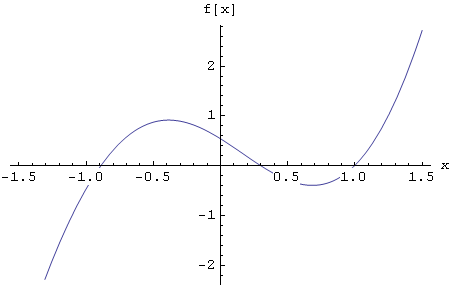
In[45]:=
![]()
Out[45]=
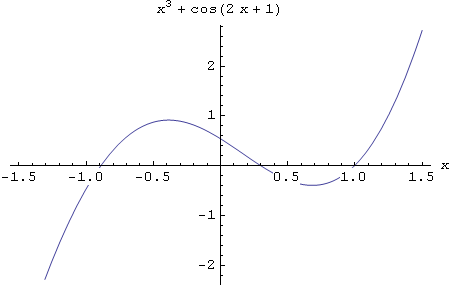
In[46]:=
![]()
Out[46]=
Opcija PlotStyle
Pomoću opcije PlotStyle možemo definirati boju, debljinu i vrstu linije.
Boju u Mathematici možemo definirati na više načina. Ovdje spominjemo samo funkciju Hue.
In[47]:=
![]()
To je funkcija koja brojevima od 0 do 1 pridružuje boju na sljedeći način:

In[48]:=
![]()
Out[48]=
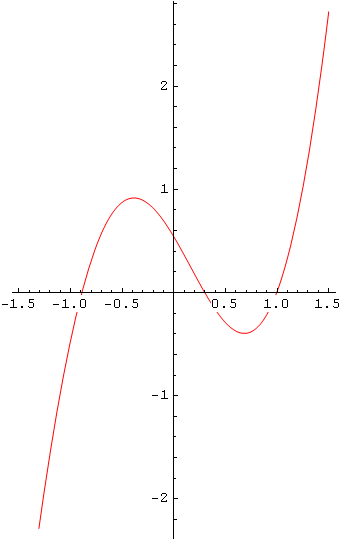
Grafovi dviju ili više funkcija nad istim intervalom
Grafove funkcija ![]() ,....,
,....,![]() : I → R, definiranih na istom intervalu I⊆R, Mathematica crta na istoj slici pomoću sljedeće naredbe:
: I → R, definiranih na istom intervalu I⊆R, Mathematica crta na istoj slici pomoću sljedeće naredbe:
● Plot[{![]() (x),....,
(x),....,![]() (x)},{x,
(x)},{x,![]() ,
,![]() }]
}]
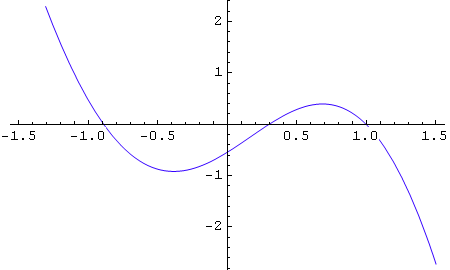
Tako na primjer definiramo funkciju g(x)=-f(x) i nacramo njezin graf.
In[49]:=
![]()
In[50]:=
![]()
Out[50]=
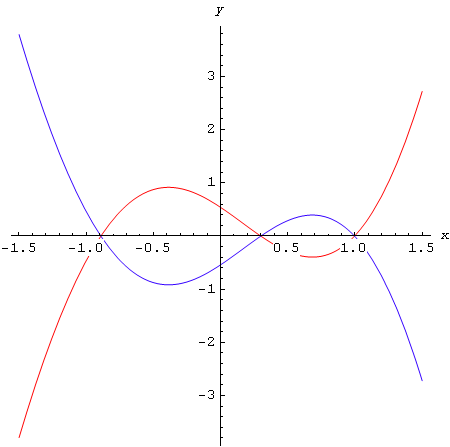
A zatim na istoj slici nacrtamo grafove funkcija f i g nad istim intervalom.
In[51]:=
![]()
Out[51]=
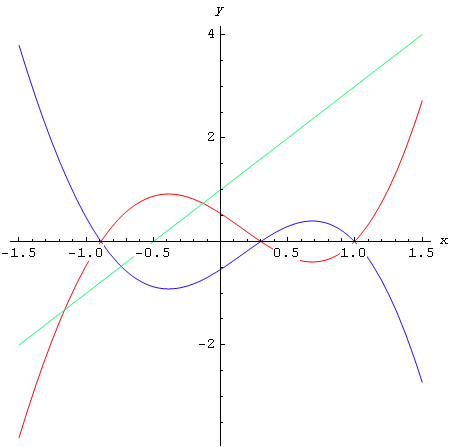
In[52]:=
![]()
Out[52]=
Primjer: Manipulate
In[53]:=
![]()
Out[53]=
Notebook izradili: Sonja Gorjanc, Vladimir Benić