Građevinski fakultet Sveučilišta u Zagrebu
Osnove inženjerske informatike II (Mathematica)
2. predavanje
Liste, vektori, matrice
LISTA je vrlo važan pojam u programu Mathematica.
Korisnik često koristi LISTU za upis inputa, a Mathematica često daje LISTU kao output.
Pojam liste
Lista je konačni niz matematičkih objekata, međusobno odvojenih zarezima, upisanih unutar vitičastih zagrada.
Matematičke objekte koji čine listu nazivamo elementima liste.
Broj elemenata liste nazivamo duljinom liste.
Elementi liste mogu biti razni matematički objekti, kao npr. brojevi, funkcije, druge liste,...... itd.
Primjeri lista
Lista duljine 3 čiji su elementi brojevi.
In[1]:=
![]()
Out[1]=
![]()
Lista duljine 4 čiji su elementi brojevi i funkcije.
In[2]:=
![]()
Out[2]=
![]()
Lista duljine 4 čiji su elementi brojevi i liste
In[3]:=
![]()
Out[3]=
![]()
Ako element liste sadrži neku Mathematica naredbu, program će tu naredbu izvršiti.
In[4]:=
![]()
Out[4]=
![]()
Ono osnovno i bitno što nam Mathematica lista omogućuje jest uređeno grupiranje izraza bilo koje vrste!
Pridruživanje vrijednosti
Mathematica naredba za pridruživanje vrijednosti nekoj varijabli je, kao što je uobičajeno u matematici, znak jednakosti =
Želimo li varijabli a pridružiti broj 3 pišemo:
In[5]:=
![]()
Out[5]=
![]()
Kad se u daljnjem računu pojavi broj a, Mathematica ga zamjenjuje s brojem 3.
In[6]:=
![]()
Out[6]=
![]()
Želimo li sada varijabli a pridružiti neku drugu vrijednost, npr. broj 2, pišemo:
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
Out[8]=
![]()
Ako želimo da Mathematica "zaboravi" pridruženu vrijednost koristimo se funkcijom Clear.
In[9]:=
![]()
In[10]:=
![]()
Out[10]=
![]()
Bitno je da korisnik ne zaboravi koju je vrijednost pridružio varijabli (pri duljem računu i većem broju varijabli to se dosta lako dogodi). Imajte stoga na umu da Mathematica "trajno pamti" vrijednost pridruženu varijabli, sve dok ju ne otklonite ili ne izađete iz programa.
VAŽNO:
Ako se, pri pridruživanju vrijednosti, s desne strane znaka jednakosti nalazi neki izraz, tada Mathematica prvo taj izraz izračuna i tek onda izvrši pridruživanje vrijednosti lijevoj strani.
Na primjer, neka je varijabli a ponovno pridružen broj 3
In[11]:=
![]()
Out[11]=
![]()
i definiramo novu varijablu var na sljedeći način:
In[12]:=
![]()
Out[12]=
![]()
Mathematica je, prije pridruživanja, izračunala desnu stranu i tek onda izvršila pridruživanje.
Znači varijabla var ima vrijednost 6, a ne ![]() .
.
To se vidi iz sljedećeg:
In[13]:=
![]()
Out[13]=
![]()
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
In[16]:=
![]()
Out[16]=
![]()
In[17]:=
![]()
Out[17]=
![]()
Vrijednost varijable var je ostala 6 kao što je i bila, budući da je u trenutku pridruživanja varijabla a imala vrijednost 3.
Napišemo li
In[18]:=
![]()
onda varijabla var gubi svoju pridruženu vrijednost.
In[19]:=
![]()
Out[19]=
![]()
Značenje znaka ;
Završimo li input znakom ; Mathematica će izvršiti zadanu operaciju, ali neće ispisati output.
In[20]:=
![]()
In[21]:=
![]()
Out[21]=
![]()
In[22]:=
![]()
Znak ; ćemo koristiti i onda kada želimo da Mathematica izvrši više naredbi, a da output ispiše samo za neke od njih.
In[23]:=
![]()
Out[23]=
![]()
Želimo li u istom inputu upisati više Mathematica naredbi, pisat ćemo ih prelaskom u novi red.
In[24]:=
![]()
Out[24]=
![]()
Out[25]=
![]()
In[26]:=

Računanje s listama
Operacije s listama zapisuju se prirodno.
In[30]:=
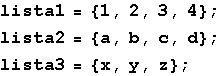
In[33]:=
![]()
Out[33]=
![]()
In[34]:=
![]()
Out[34]=
![]()
In[35]:=
![]()
Out[35]=
![]()
Linearne kombinacije lista mogu se računati samo za liste istih duljina.
In[36]:=
![]()
![]()
Out[36]=
![]()
In[37]:=
![]()
Out[37]=
![]()
In[38]:=
![]()
Out[38]=
![]()
In[39]:=
![]()
Out[39]=
![]()
Lista se može potencirati samo s listom iste duljine.
In[40]:=
![]()
![]()
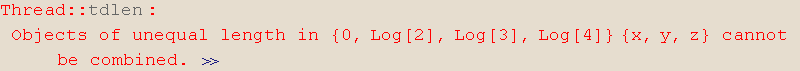
Out[40]=
![]()
In[41]:=
![]()
Out[41]=
![]()
In[42]:=
![]()
Značenje znaka //
Znak // u Mathematici se može upotrijebiti za izvršenje nekih naredbi, umjesto uglatih zagrada.
Na primjer, umjesto
In[43]:=
![]()
Out[43]=
![]()
možemo pisati
In[44]:=
![]()
Out[44]=
![]()
Funkcije koje djeluju na listama
Popis osnovnih funkcija koje djeluju na listama je:
Length[lista] - broj elemenata liste (duljina liste)
First[lista] - prvi element liste
Last[lista] - zadnji element liste
Rest[lista] - lista iz koje je izbačen prvi element
lista[[i]] - i-ti element liste
lista[[{i,j}]] - i-ti i j-ti element liste
lista[[{i,j,k,...}]] - i-ti, j-ti, k-ti,..... element liste
Obratite pažnju na dvije lijeve i dvije desne uglate zagrade. Dvostruke uglate zagrade u Mathematici se upotrbljavaju za indeksiranje.
Primjeri
Varijabli a pridružimo listu {1, 2, 4, 8, 16}
In[45]:=
![]()
• Izračunajte kosinus zadnjeg člana liste a (decimalni prikaz).
In[46]:=
![]()
Out[46]=
![]()
• Potencirajte sve elemente liste a s brojem elemenata liste a.
In[47]:=
![]()
Out[47]=
![]()
• Kvadrirajte sve elemente liste a osim prvog.
In[48]:=
![]()
Out[48]=
![]()
• Potencirajte treći element liste a sa njenim četvrtim elementom.
In[49]:=
![]()
Out[49]=
![]()
• Formirajte listu čiji su elementi redom: 5., 3. i 2. element liste a.
In[50]:=
![]()
Out[50]=
![]()
In[51]:=
![]()
Lista tablice vrijednosti -- naredbe TableForm i Table
TableForm
Želimo li da Mathematica ispiše listu u formi tablice, koristimo naredbu TableForm koja djeluje na sljedeći način:
In[52]:=
![]()
Out[52]//TableForm=
| 1 |
| 2 |
| 3 |
Zbog preglednosi inputa nju je, gotovo redovito, bolje zapisivati pomoću znaka //
In[53]:=
![]()
Out[53]//TableForm=
| 1 |
| 2 |
| 3 |
Ako su elementi liste druge liste, tablična forma je sljedeća:
In[54]:=
![]()
Out[54]//TableForm=
| 1 | 2 | 3 |
| a | b | c |
In[55]:=
![]()
Out[55]//TableForm=
| 1 | 2 | 3 |
| a | b | c |
| x | y | z |
In[56]:=
![]()
Out[56]//TableForm=
| 1 | 2 | 3 | |
| a | b | ||
| x | y | z | w |
Table
Tablicu vrijednosti u Mathematici formiramo funkcijom Table.
Rezultat je lista vrijednosti.
Funkcija Table ima slijedeću sintaksu:
● Table[f(i), {i, i![]() }]
}]
daje listu funkcijskih vrijednosti f(i), kada i poprima vrijednosti prirodnih brojeva od 1 do i![]() , s korakom 1.
, s korakom 1.
In[57]:=
![]()
Out[57]=
![]()
In[58]:=
![]()
Out[58]=
![]()
● Table[f(i), {i,i![]() , i
, i![]() }]
}]
daje listu funkcijskih vrijednosti f(i), kada i poprima vrijednosti realnih brojeva od i![]() do i
do i![]() , s korakom 1.
, s korakom 1.
In[59]:=
![]()
Out[59]=
![]()
● Table[f(i), {i,i![]() , i
, i![]() ,d
,d![]() }]
}]
daje listu funkcijskih vrijednosti f(i), kada i poprima vrijednosti realnih brojeva od i![]() do i
do i![]() , s korakom d
, s korakom d![]() .
.
In[60]:=
![]()
Out[60]=
![]()
● Table[f(i,j), {i,i![]() , i
, i![]() ,d
,d![]() },{j,j
},{j,j![]() , j
, j![]() ,d
,d![]() }]
}]
daje dvodimenzionalnu listu funkcijskih vrijednosti f(i,j), kada i poprima vrijednosti realnih brojeva od i![]() do i
do i![]() , s korakom d
, s korakom d![]() , a j poprima vrijednosti realnih brojeva od j
, a j poprima vrijednosti realnih brojeva od j![]() do j
do j![]() , s korakom d
, s korakom d![]() ,
,
TABLICA MNOŽENJA
In[61]:=
![]()
Out[61]=

In[62]:=
![]()
Out[62]//TableForm=
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
TABLICA BINOMNIH KOEFICIJENATA (Pascalov trokut)
In[63]:=
![]()
Out[63]//TableForm=
| 1 | |||||||
| 1 | 1 | ||||||
| 1 | 2 | 1 | |||||
| 1 | 3 | 3 | 1 | ||||
| 1 | 4 | 6 | 4 | 1 | |||
| 1 | 5 | 10 | 10 | 5 | 1 | ||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
In[64]:=
![]()
Out[64]//TableForm=
| 1 | 1 |
| a+b | a+b |
Naravno da indeksi NE MORAJU imati oznake i i j, već za varijablu možete koristiti bilo koju drugu odgovarajuću oznaku.
Vektorski račun
U programskom sustavu Mathematica vektori su reprezentirani listama njihovih skalarnih komponenata.
Vektori u ravnini - listama duljine 2.
Vektori u prostoru - listama duljine 3.
Mi ćemo u našim primjerima računati s vektorima u prostoru, ali se sva ona izlaganja koja nisu specifična samo za prostor, mogu primijeniti na ravninu - ukidanjem treće skalarne komponente.
Zadavanje vektora
Neka su ![]() i
i ![]() vektori u prostoru
vektori u prostoru
![]() = 4
= 4![]() + 3
+ 3![]() -
- ![]()
![]() = -
= -![]() + 6
+ 6![]() +2
+2![]()
U Mathematici ćemo ih zadati listama njihovih skalarnih komponenata.
In[65]:=
![]()
Množenje vektora skalarom (realnim brojem)
Množenje vektora ![]() sa skalarom (na primjer 1.5) izračunati ćemo na sljedeći način
sa skalarom (na primjer 1.5) izračunati ćemo na sljedeći način
In[67]:=
![]()
Out[67]=
![]()
ili
In[68]:=
![]()
Out[68]=
![]()
ili
In[69]:=
![]()
Out[69]=
![]()
i očitati rješenje
![]() = 6
= 6![]() + 4.5
+ 4.5![]() - 1.5
- 1.5![]()
Linearna kombinacija vektora
Vektor ![]() = 6
= 6![]() - 1.5
- 1.5![]() izračunati ćemo
izračunati ćemo
In[70]:=
![]()
Out[70]=
![]()
i očitati rješenje
![]() = 25.5
= 25.5![]() + 9
+ 9![]() - 9
- 9![]()
Skalarni produkt vektora
Operacija skalrnog množenja vektora u Mathematici se označava točkom ( . ).
Stoga skalrni produkt vektora ![]() i
i ![]() računamo:
računamo:
In[71]:=
![]()
Out[71]=
![]()
Vektorski produkt vektora
Mathematica naredba za operaciju vektorskog množenja vektora je Cross.
Stoga vektorski produkt ![]() ×
× ![]() računamo
računamo
In[72]:=
![]()
Out[72]=
![]()
i očitavamo rješenje rješenje
![]() ×
× ![]() = 12
= 12![]() -7
-7![]() +27
+27![]()
Modul vektora
Budući da je |![]() | =
| =![]() , modul vektora
, modul vektora ![]() u Mathematici računamo:
u Mathematici računamo:
In[73]:=
![]()
Out[73]=
![]()
Kut između vektora
Budući je cos∠(![]() )=
)=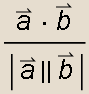 , kut između vektora
, kut između vektora ![]() i
i ![]() u Mathematici računamo:
u Mathematici računamo:
In[74]:=
![]()
Out[74]=
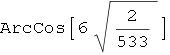
In[75]:=
![]()
Out[75]=
![]()
Dobivena vrijednost je u radijanima. Rezultat u stupnjevima dobivamo na sljedeći način:
In[76]:=
![]()
Out[76]=
![]()
In[77]:=
![]()
Matrični račun
U programskom sustavu Mathematica matrice su reprezentirane listama lista.
Prikazuju se kao liste svojih redaka, a retci kao liste svojih elemenata.
Naravno, svi retci neke matrice moraju imati isti broj elemenata
Na primjer, ovo je jedna 3×2 matrica.
In[78]:=
![]()
Out[78]=
![]()
Output u uobičajenom zapisu dobivamo naredbom MatrixForm.
In[79]:=
![]()
Out[79]//MatrixForm=
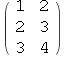
Matricu možemo dobiti pomoću naredbe Table.
Table[f(i,j),{i,n},{j,m}] tvori n×m matricu.
In[80]:=
![]()
Out[80]//MatrixForm=
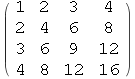
Neke naredbe
● Table[f(i,j),{i,n},{j,m}] tvori n×m matricu.
In[81]:=
![]()
Out[81]//MatrixForm=
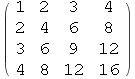
● IdentityMatrix[n] tvori jediničnu matricu n×n.
In[82]:=
![]()
Out[82]//MatrixForm=
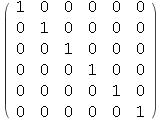
● DiagonalMatrix[{![]() ,....,
,....,![]() }]
}]
tvori n×n matricu s elementima liste {![]() ,....,
,....,![]() } na glavnoj dijagonali, a ostalima elementima jednakim 0.
} na glavnoj dijagonali, a ostalima elementima jednakim 0.
In[83]:=
![]()
Out[83]//MatrixForm=
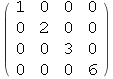
Računanje s matricama
In[84]:=
![]()
In[85]:=
![]()
In[87]:=
![]()
Out[87]//MatrixForm=
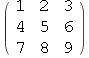
Out[88]//MatrixForm=
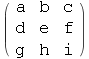
In[89]:=
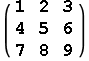
Out[89]=
![]()
● Matricu množimo brojem tako da listu pomnožimo s tim brojem.
● Matrice zbrajamo i oduzimamo tako da zbrajamo i oduzimamo pripadne liste.
In[90]:=
![]()
Out[90]//MatrixForm=
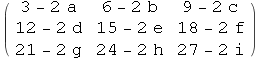
● Matrice međusobno množimo pomoću znaka . (točka). NE mogu se pomnožiti bilo koje dvije matrice.
In[91]:=
![]()
Out[91]//MatrixForm=
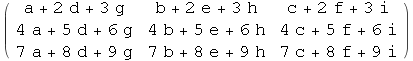
Imajte na umu da množenje matrica nije isto što i množenje lista pa treba obratiti pažnju na mogućunost zabune. Naime, zapis m1*m2 - NEĆE dati produkt matrica, već listu produkata elemenata liste m1 s odgovarajućim elementima liste m2.
In[92]:=
![]()
Out[92]//MatrixForm=
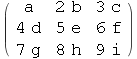
● Ako je matrica kvadratna (broj redaka = broju stupaca) možemo joj izračunati determinantu funkcijom Det.
In[93]:=
![]()
Out[93]=
![]()
Out[94]=
![]()
● Ako je delterminanta kvadratne matrice različita od nule, inverznu matricu računamo funkcijom Inverse.
In[95]:=
![]()
Out[95]//MatrixForm=
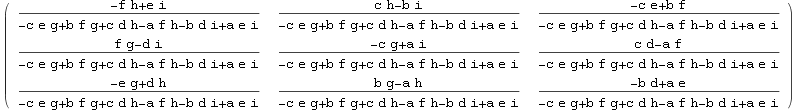
● MatrixPower[m1,n] daje n-tu potenciju matrice m1.
In[96]:=
![]()
Out[96]//MatrixForm=
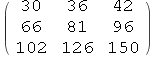
● Transpose[m1] daje transponiranu matricu matrice m1.
In[97]:=
![]()
Out[97]//MatrixForm=
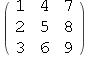
Notebook izradili: Sonja Gorjanc, Vladimir Benić