Za funkciju f :I->R kažemo da je konveksna na intervalu I=(a,b) (a<b),
ako za svaki λ, (0<λ<1)
f[ λ
Za funkciju f :I->R kažemo da je konkavna na intervalu I=(a,b) (a<b),
ako za svaki λ, (0<λ<1)
f[ λ
Definicija 6. KONVEKSNA I KONKAVNA FUNKCIJA
Za funkciju f :I->R kažemo da je konveksna na intervalu I=(a,b) (a<b),
ako za svaki λ, (0<λ<1)
f[ λ ![]() (1-λ)
(1-λ) ![]() ] <= λ f(
] <= λ f(![]() )+(1-λ)f(
)+(1-λ)f(![]() ), za svaki
), za svaki ![]() ,
,![]()
Za funkciju f :I->R kažemo da je konkavna na intervalu I=(a,b) (a<b),
ako za svaki λ, (0<λ<1)
f[ λ ![]() (1-λ)
(1-λ) ![]() ] >= λ f(
] >= λ f(![]() )+(1-λ)f(
)+(1-λ)f(![]() ), za svaki
), za svaki ![]() ,
,![]()
Napomena
Za λ=![]() , f KONVEKSNA ako f(
, f KONVEKSNA ako f( ![]() )<=
)<=![]() ( f(
( f(![]() )+f(
)+f(![]() ) )
) )
f KONKAVNA ako f( ![]() ) >=
) >=![]() ( f(
( f(![]() )+f(
)+f(![]() ) )
) )
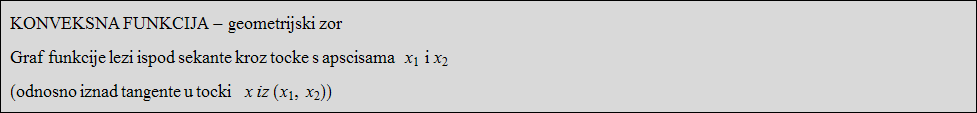
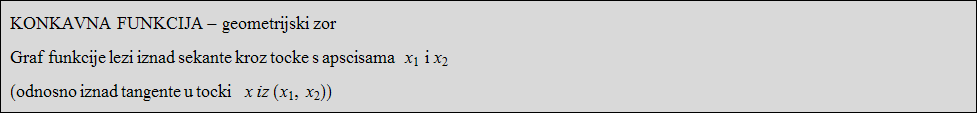
![[Graphics:../HTMLFiles/index_76.gif]](../HTMLFiles/index_76.gif)
Converted by Mathematica (September 20, 2003)