Ponovimo svojstva hiperboličkog paraboloida! (HIPAR)
Za dani hipar i istaknutu proizvoljnu točku T cilj nam je odrediti asimptotske i glavne smjerove, krivulje normalnih presjeka koje pripadaju tim smjerovima te dati neke vizualizacije vezane za funkcije Gaussove i srednje zakrivljenosti hipara.
Dirna ravnina hipara u bilo kojoj njegovoj točki T (sve točke hipara su regularne) siječe taj hipar po dvije izvodnice koje pripadaju različitim sistemima. Normala n okomita je na dirnu ravninu t i prolazi točkom T. Svi pravci pramena (T) u dirnoj ravnini t tangente su krivulja koje leže na hiparu, a dirališta su im u točki T.
Postavljamo ravnine pamena [n] (ravnine normalnog presjeka kroz T) i promatramo presjeke hipara s tim ravninama.
U točki T mjerimo zakrivljenost svakog takvog presjeka.
Funkcija zakrivljenosti normalnih presjeka kroz T na intervalu
[0,π] poprima ekstremne vrijednosti za kutove koji odgovaraju glavnim smjerovima, a jednaka je 0 za kutove koji odgovaraju asimptotskim smjerovima.
Asimptotske smjerove hipara u točki T određuju njegove dvije izvodnice kroz T.
Glavni smjerovi hipara u točki T određeni su simetralama kuta asimptotskih smjerova.
Sljedeće slike prikazuju krivulje normalnih presjeka kroz glavne i asimptotske smjerove, te graf funkcije normalne zakrivljenosti hipara u točki T
Vizualizacije Gaussove i srednje zakrivljenosti na hiperboličkom parabloidu
U programu Mathematica postoji periodička funkcija
Hue (period 1)
koja realnom broju pridružuje boju na sljedeći način:
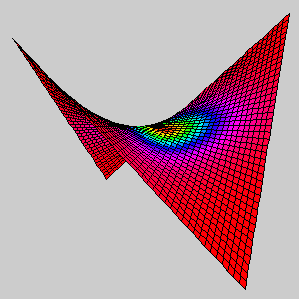Hiperbolički parabloid obojan bojom koja je funkcija njegove Gaussove zakrivljenosti.
|
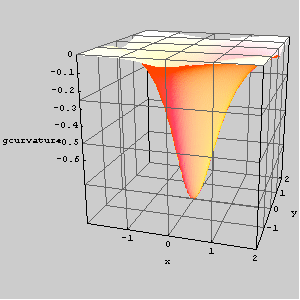Graf funkcije Gaussove zakrivljenosti istog hipara nad područjem [-2,2]×[-2,2].
|
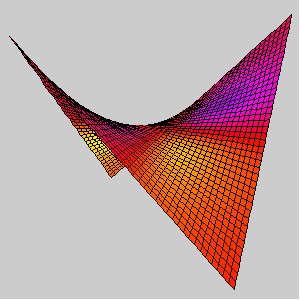Hiperbolički parabloid obojan bojom koja je funkcija njegove srednje zakrivljenosti.
|
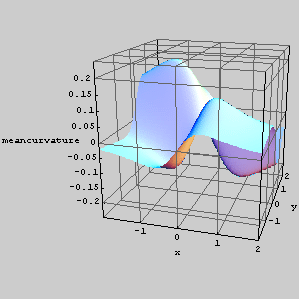Graf funkcije srednje zakrivljenosti istog hipara nad područjem [-2,2]×[-2,2].
|
webMathematica datoteka za vježbu
Vizualizacije Gaussove i srednje zakrivljenosti regularne plohe
|
natrag