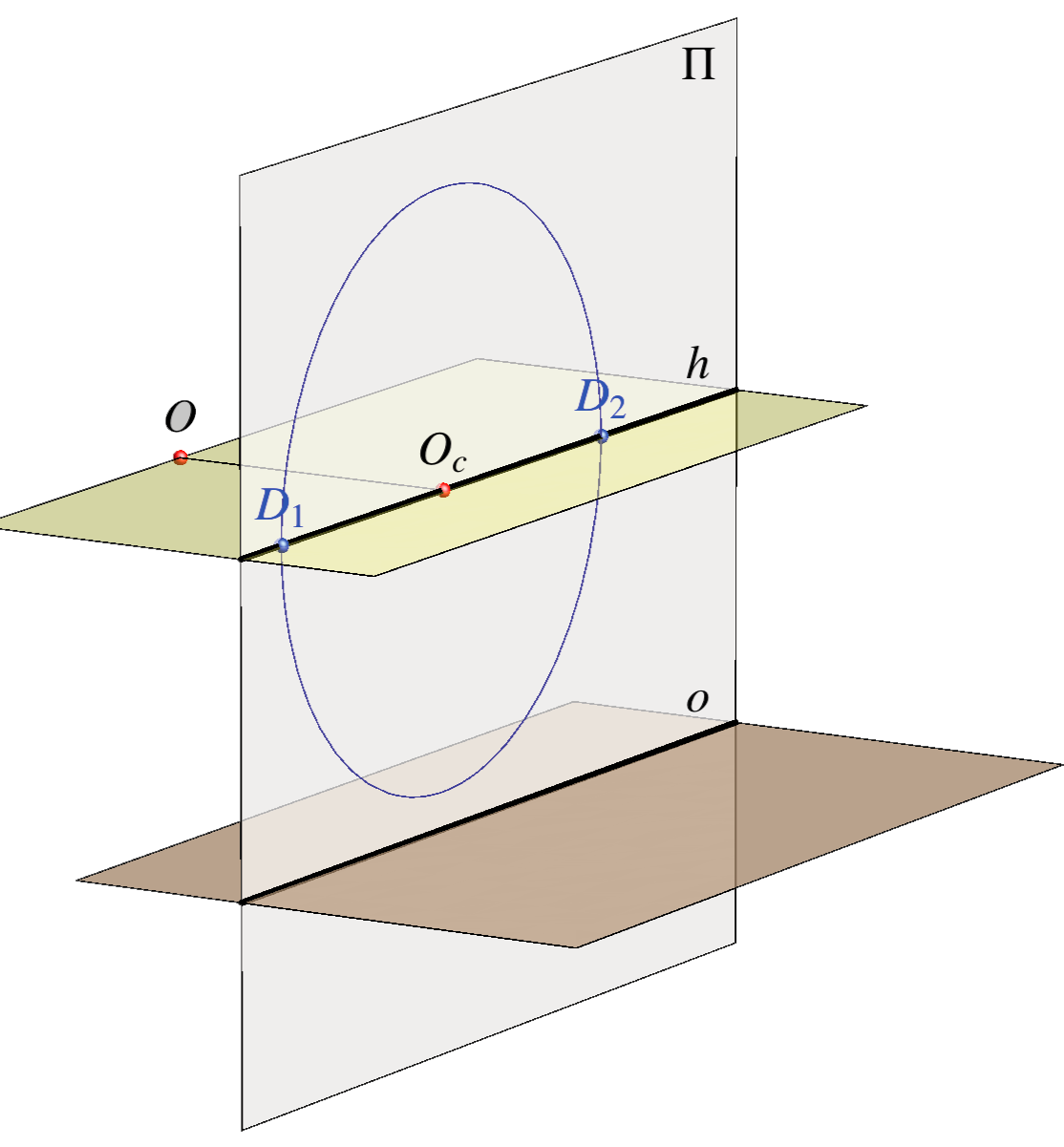
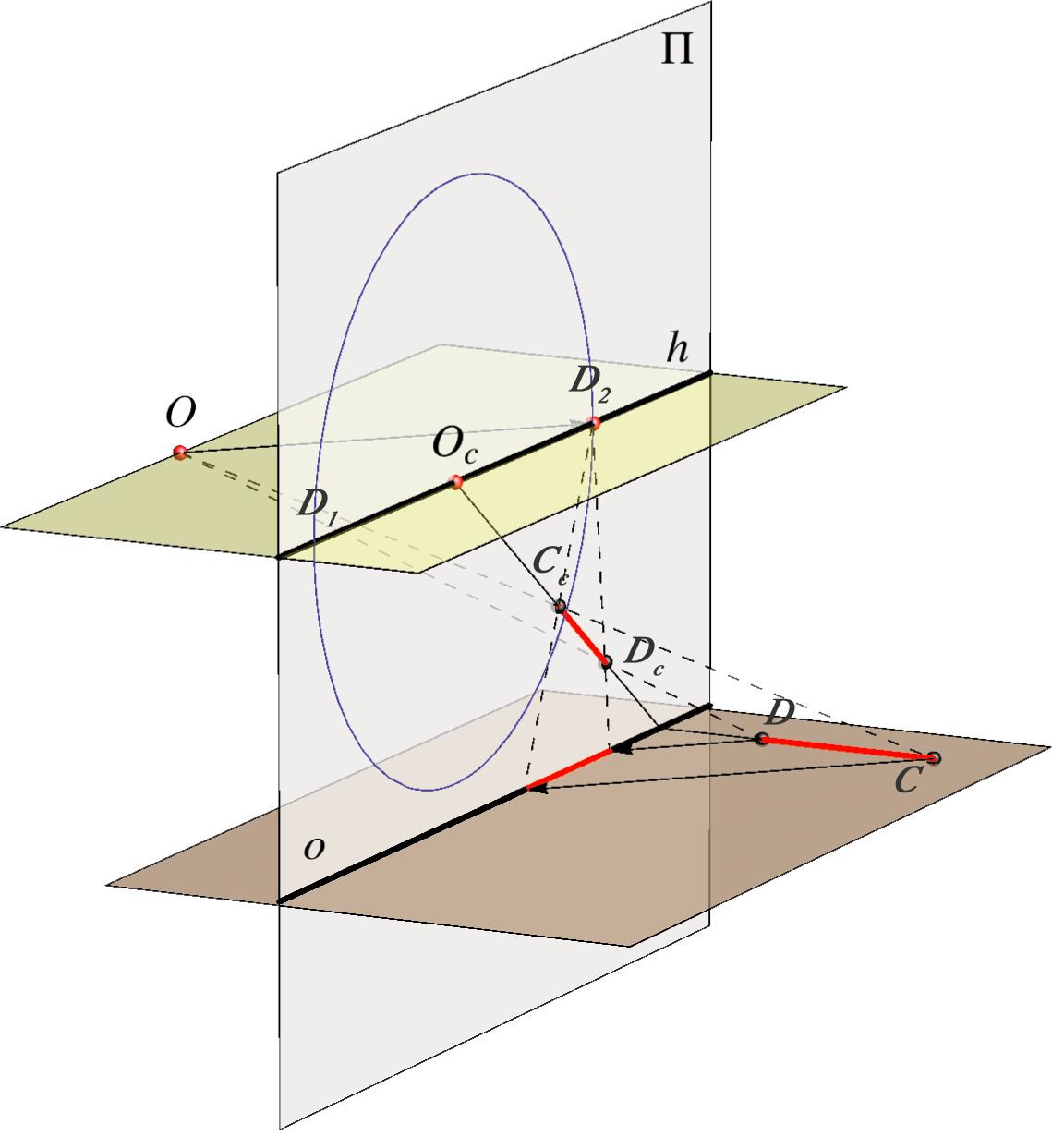
pravi trag horizontalne ravnine
\( h\) – horizont
nedogledni trag horizontalne ravnine
\( D_1, D_2 \) – distancijske točke
nedogledi pravaca horizontalne ravnine s priklonim kutem od \( 45^\circ\)
 |
\( o\) – osnovica pravi trag horizontalne ravnine \( h\) – horizont nedogledni trag horizontalne ravnine \( D_1, D_2 \) – distancijske točke nedogledi pravaca horizontalne ravnine s priklonim kutem od \( 45^\circ\) |
 |
 |
 |
 |
 |
 |
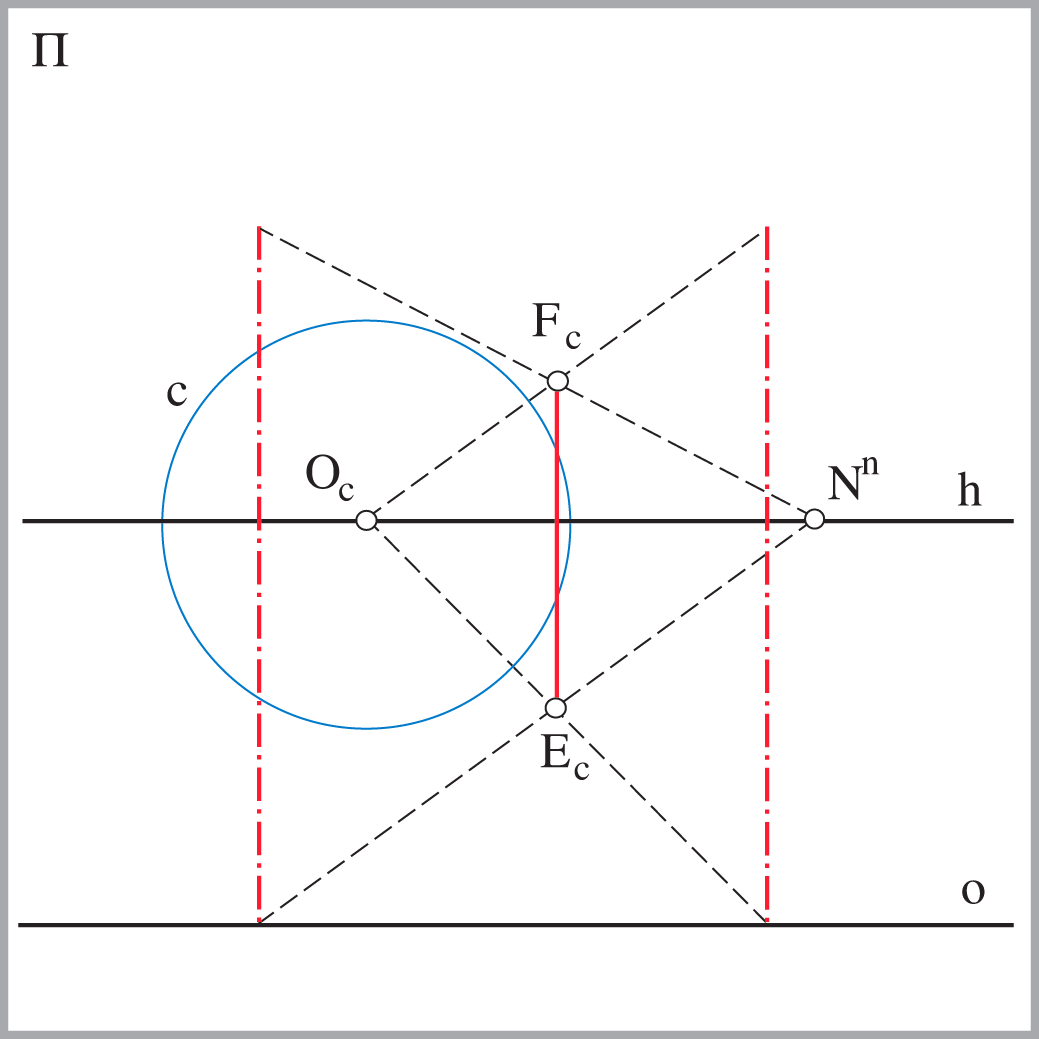
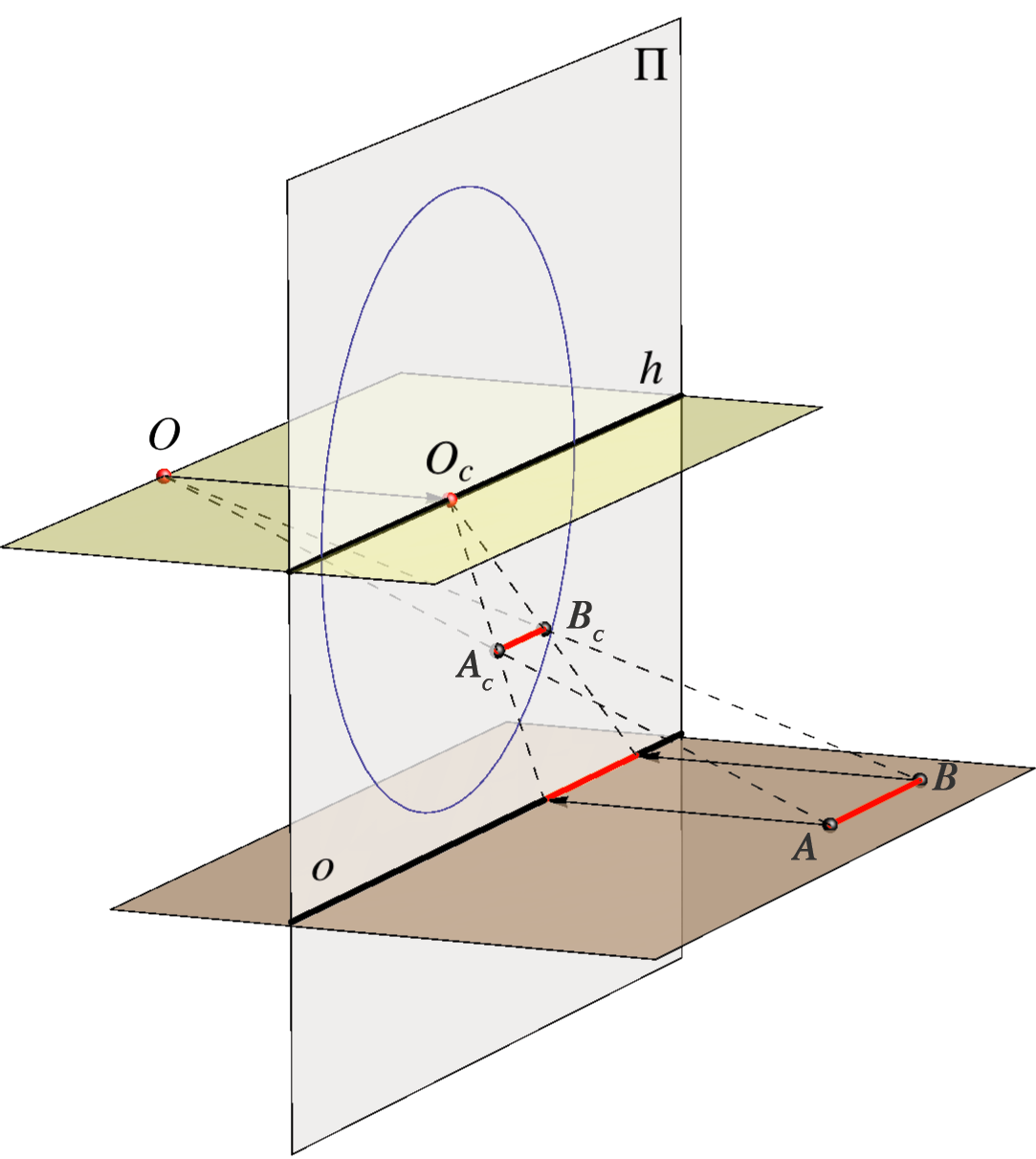
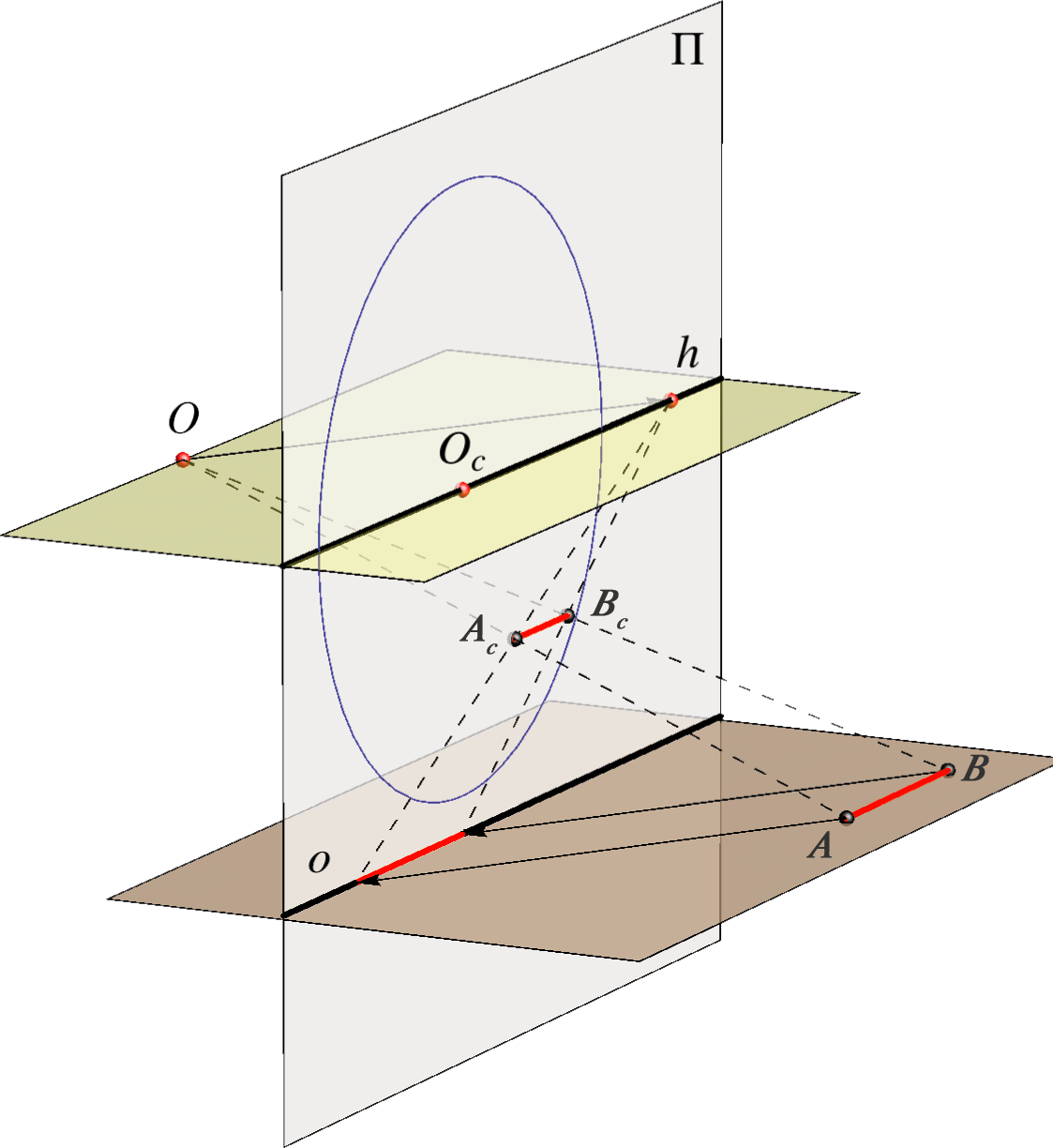
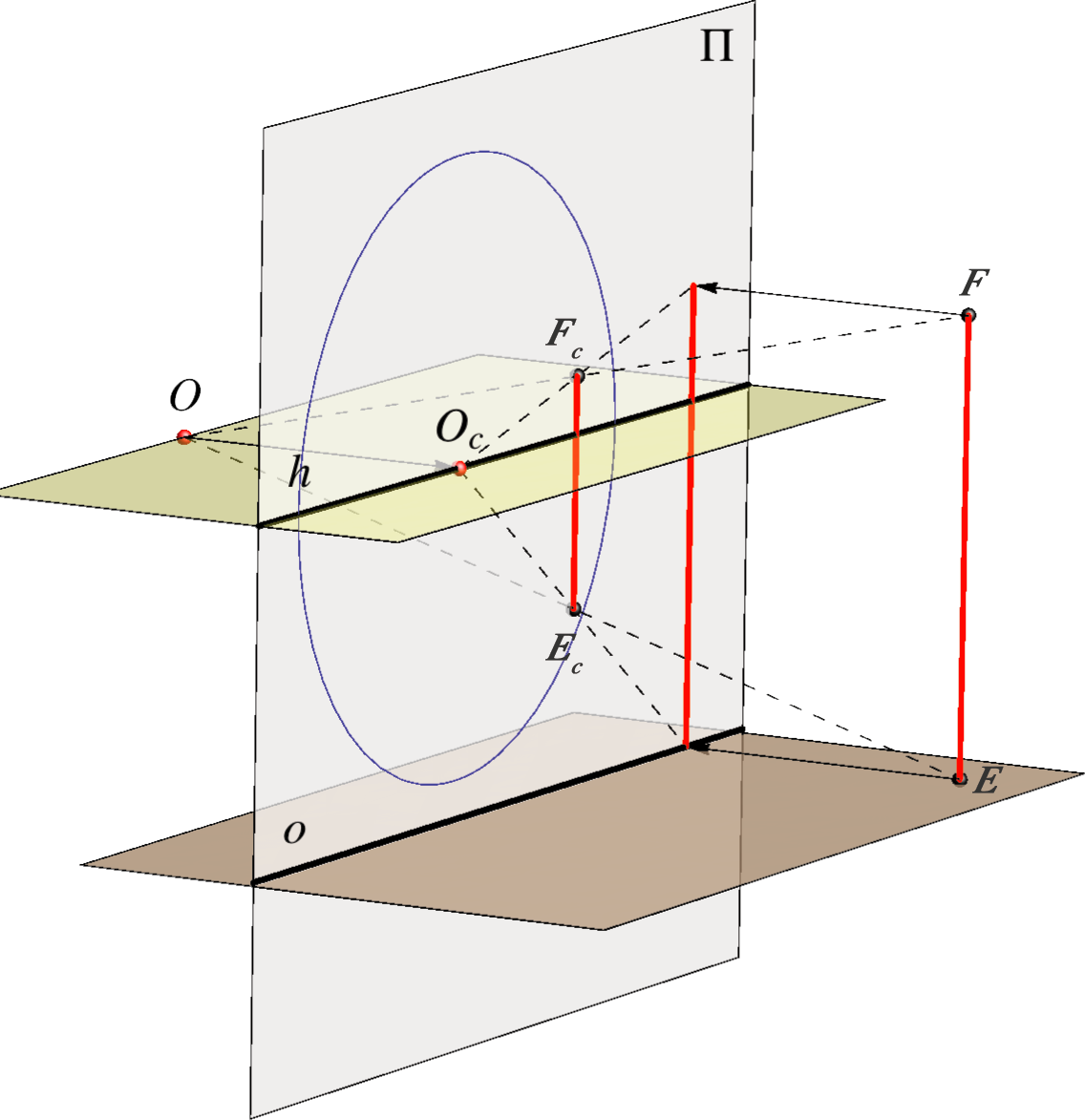
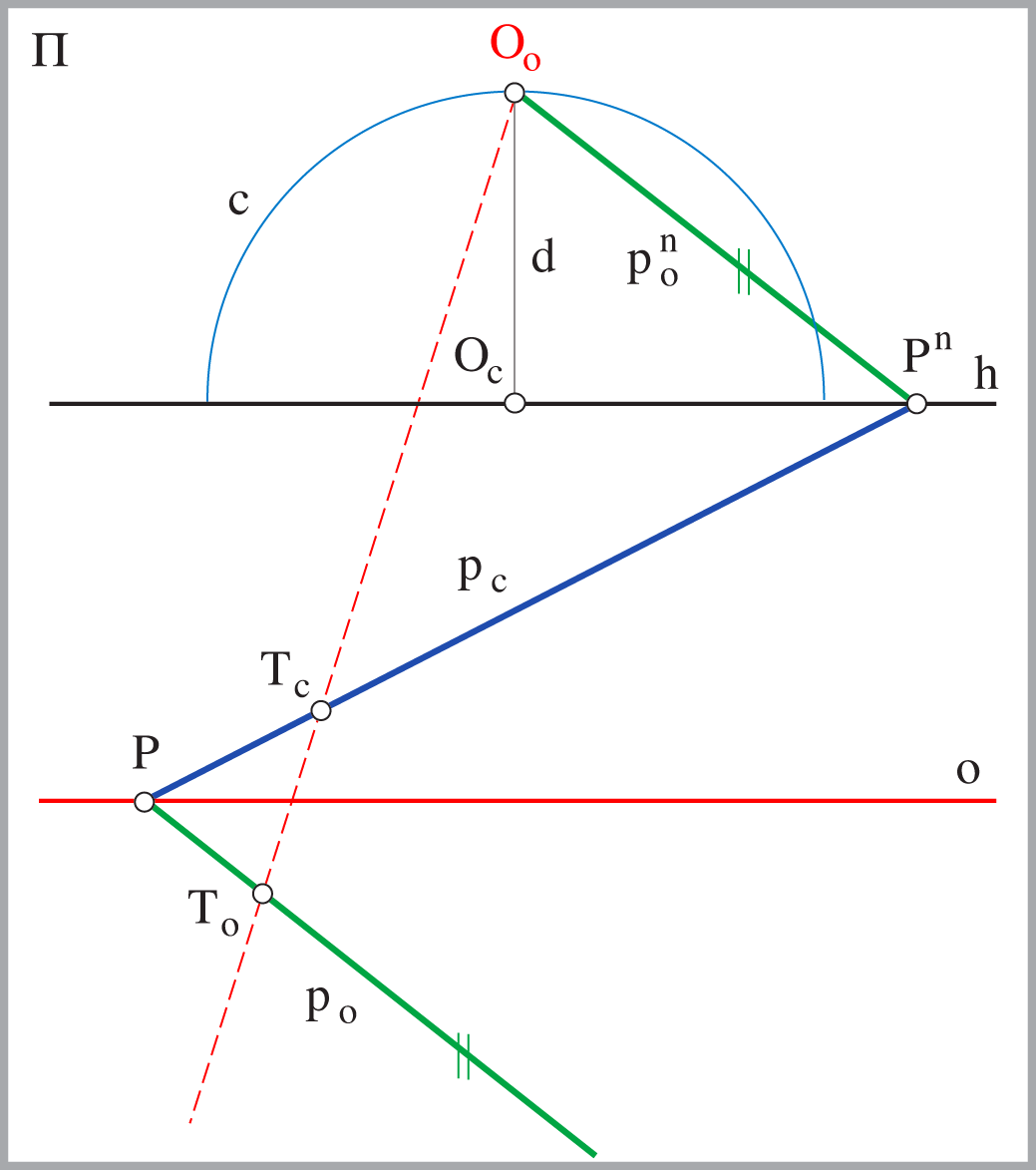
Za svaki pravac \(p(P,P^n)\) horizontalne ravnine, koji je u općem položaju prema zadanim elementima projekcije, vrijedi: \(p_\circ \parallel O_\circ P^n\).
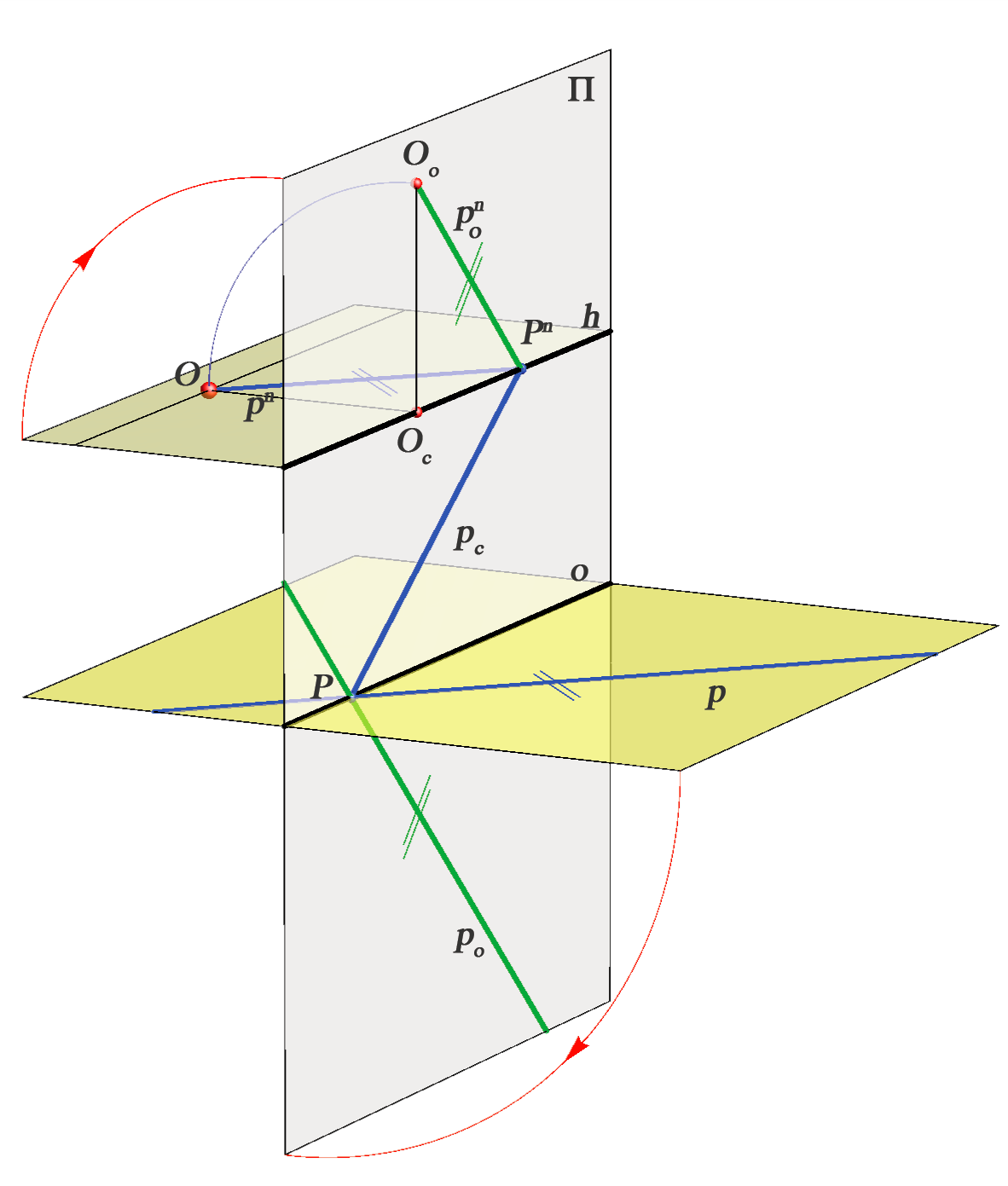 |
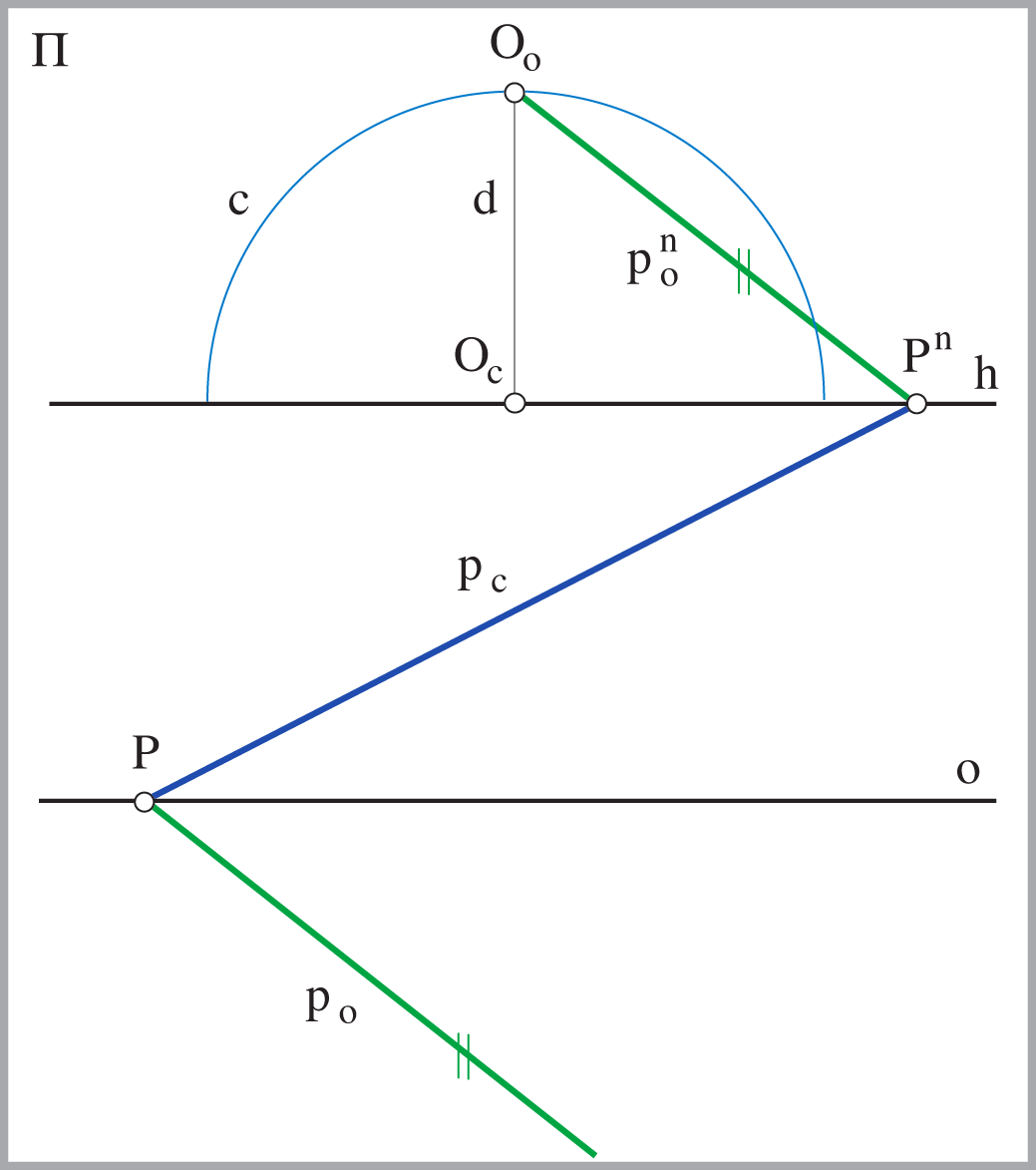 kojoj je \(O^\circ\) središte, a os pravac \(o\). |
Za svaku točku \(T\) horizontalne ravnine, koja je u općem položaju prema zadanim elementima projekcije, vrijedi:
bijekcija \(T_c \longleftrightarrow T_\circ \) je perspektivna kolineacija kojoj je \(O_\circ\) središte, a pravac \(o\) os, tj. \((o, O_\circ, T_c, T_\circ)\).
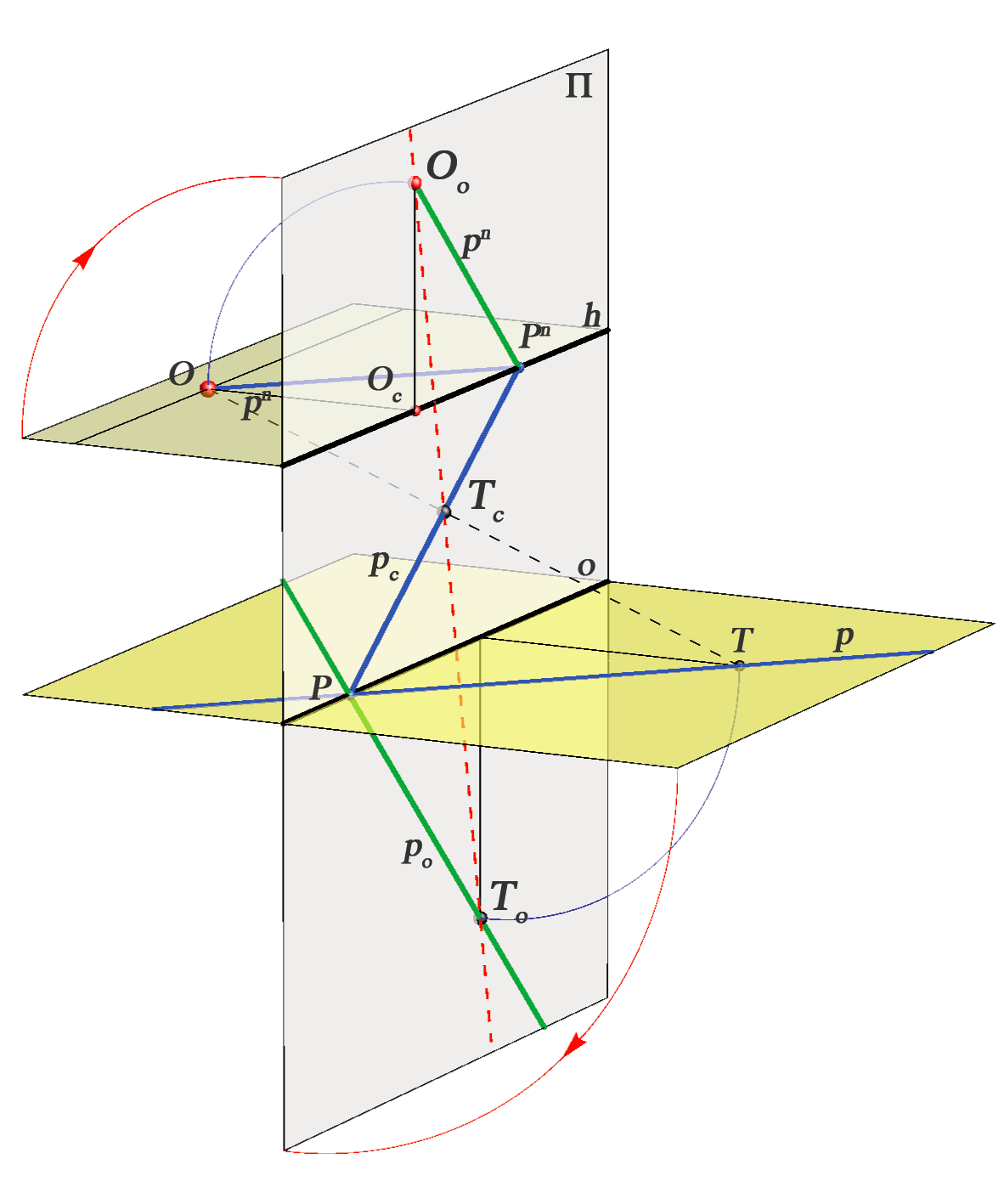 |
 |
|
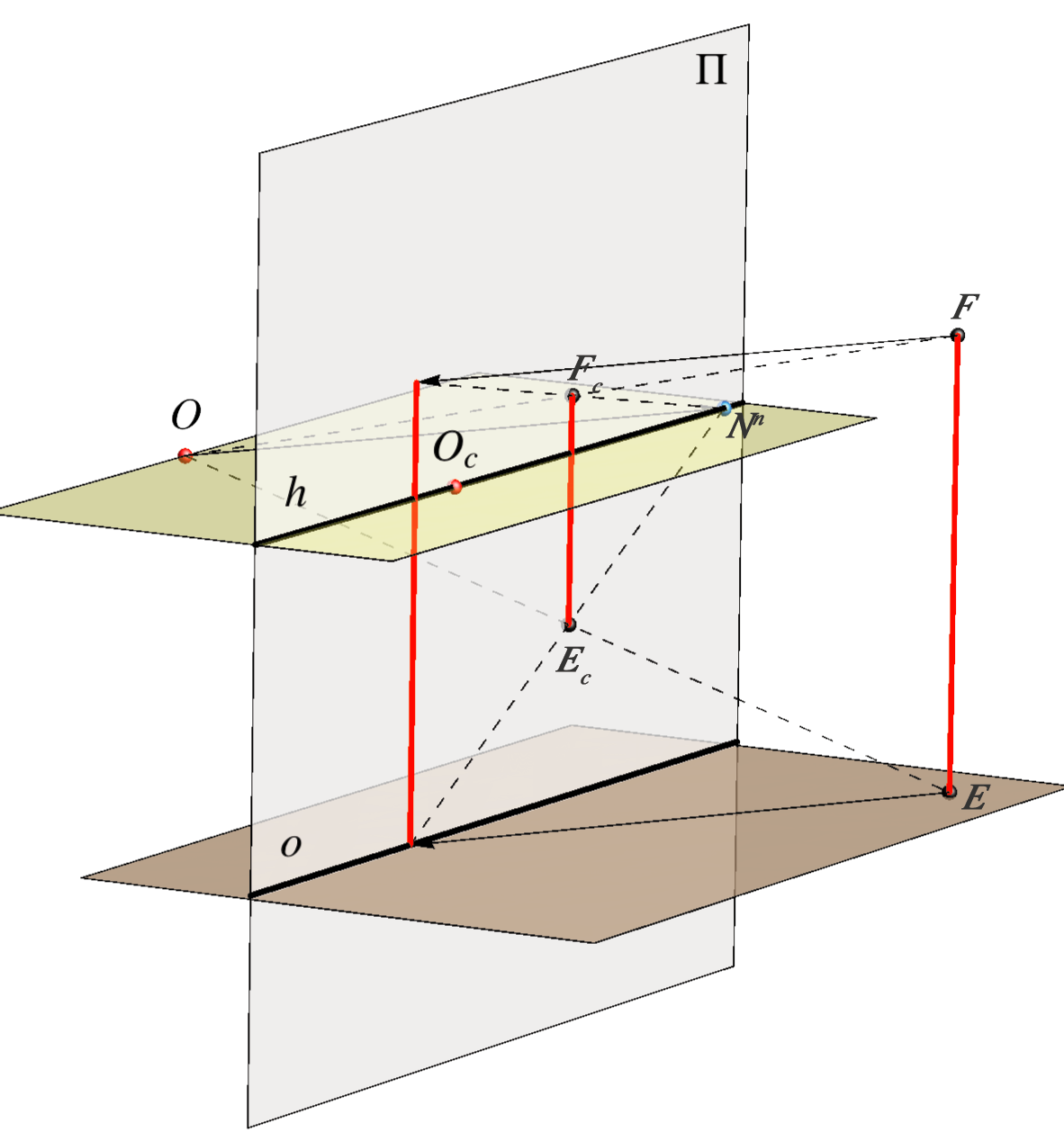
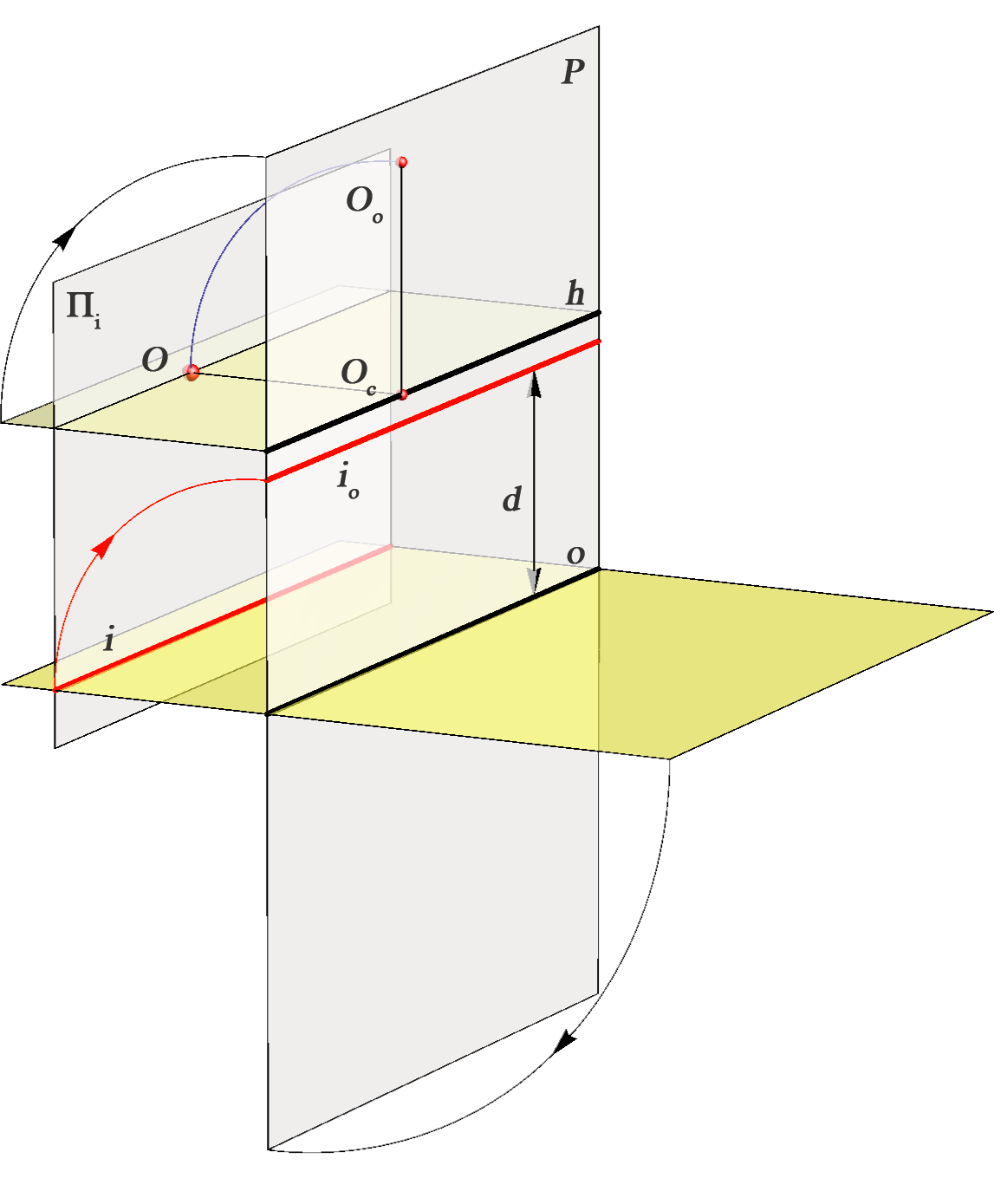
pravac ravnine čije se točke projiciraju u beskonačnost Izbježnica je presjek horizontalne i izbježne ravnine. |
 |
Ponovite: Klasifikacija konika
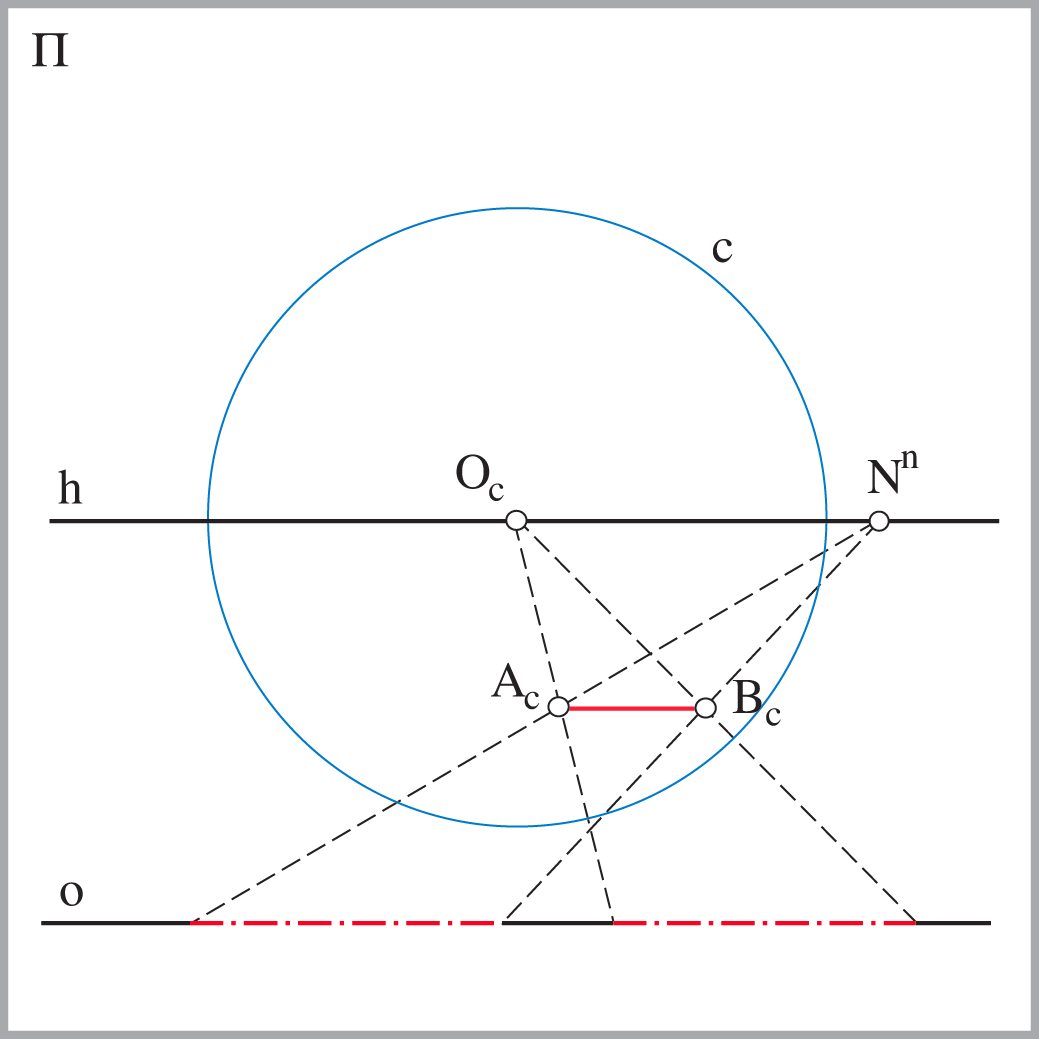
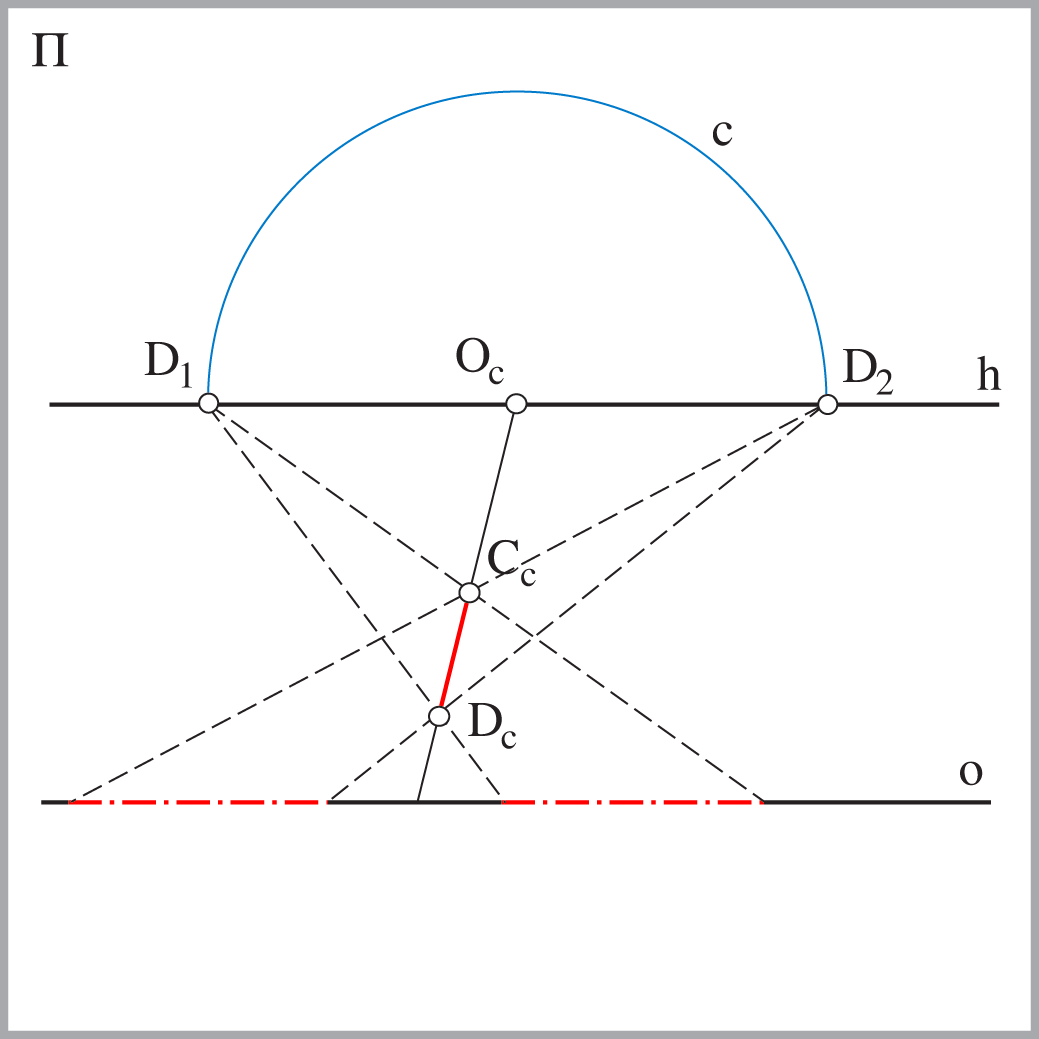
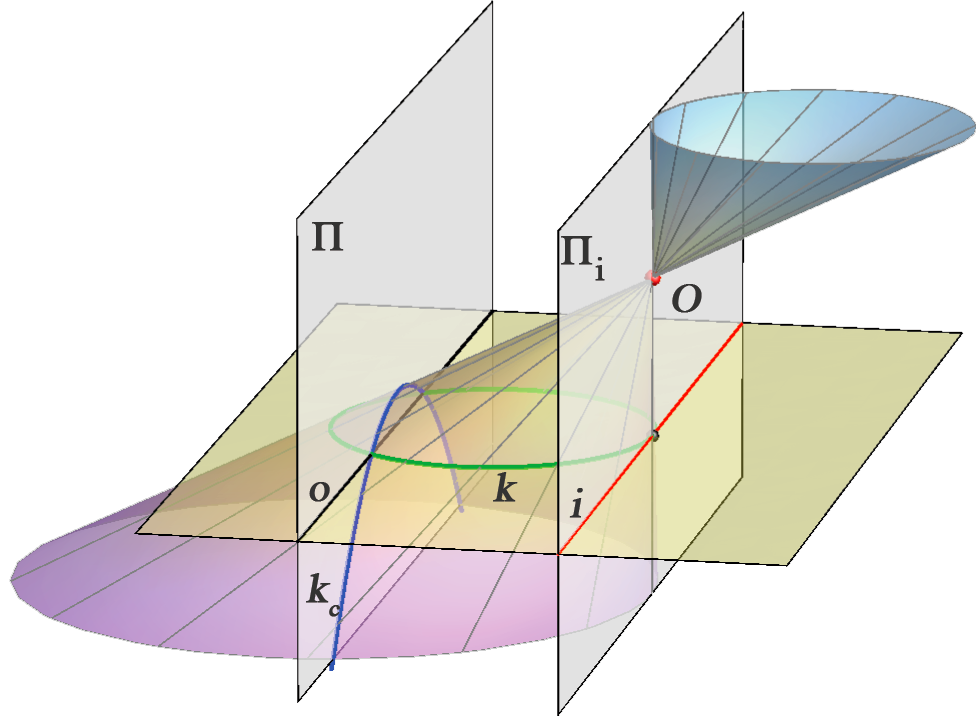
Perspektivna slika kružnice je elipsa, parabola ili hiperbola.
 \(k_c -\) elipsa kružnica \(k\) i izbježna ravnina nemaju zajedničkih točaka |
 \(k -\) parabola kružnica \(k\) dodiruje izbježnu ravninu |
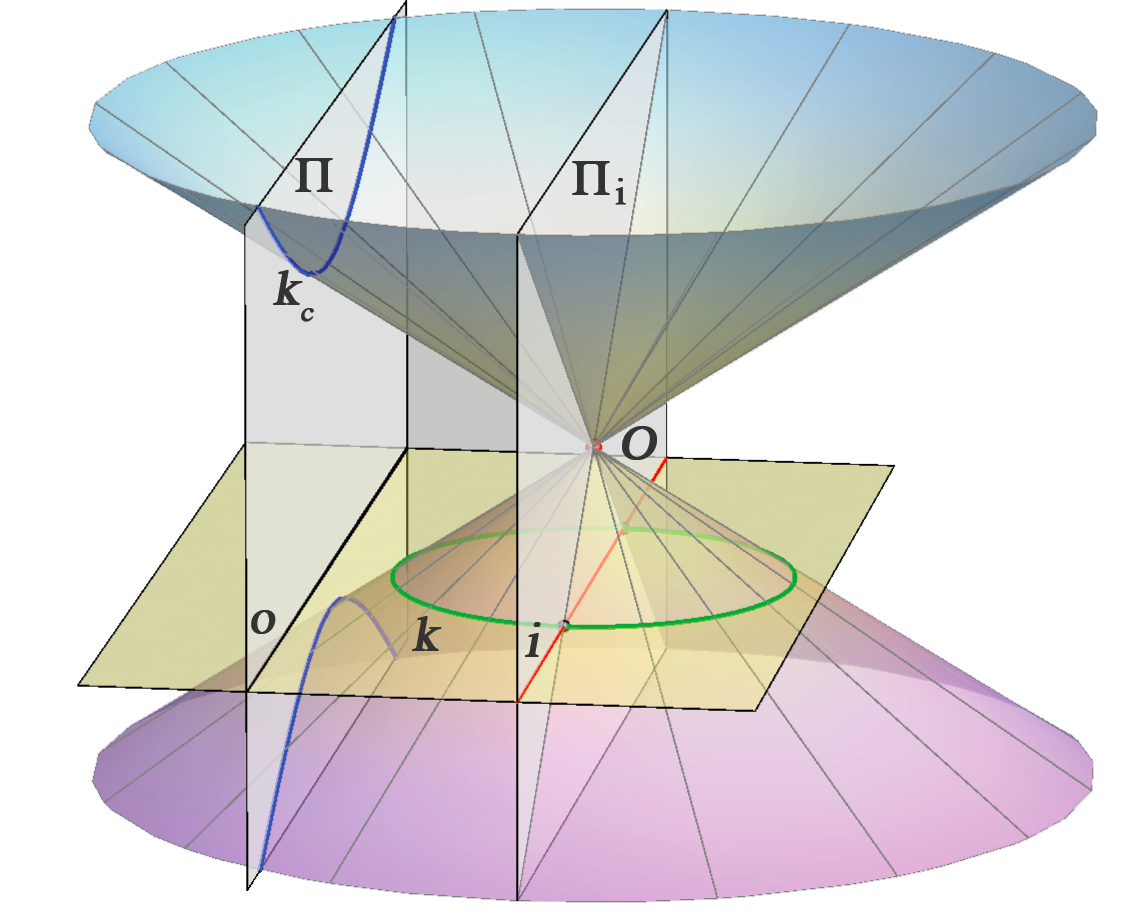 \(k -\) hiperbola kružnica \(k\) siječe izbježnu ravninu |
Materijali za studente arhitekture:
Perspektiva kružnice 1,
Perspektiva kružnice 2

izradila Sonja Gorjanc - PERSPEKTIVA (predavanja)