Solids

There are two basic types of solids - polyhedra and curved solids.

Polyhedra

Polyhedron is a solid object bounded by polygonal faces.
Polygonal faces are also called sides, their vertices are called vertices of the polyhedron and the line segments connecting the adjacent vertices are called edges of the polyhedron.
Line segment connecting the vertices that lie on different faces is called a diagonal .
Polyhedron is convex if its suface does not intersect itself and the diagonals lie in the interior of the polyhedron. We will be interested only in convex polyhedra.


Convex polyhedron – RECTANGULAR BOX Non-convex polyhedron

Platonic solids

Regular polyhedron has congruent regular polygonal faces with the same number of faces meeting at each vertex.
There are five such polyhedra and they are called Platonic solids. They are:
tetrahedron

hexahedron (cube)


octahedron


dodecahedronREMINDER construction of the regular pentagon


icosaedron


Prisms

A prism is a polyhedron with two congruent parallel polygonal bases and its faces are parallelograms.
Those parallelogram faces are also called lateral faces. All lateral faces form a lateral surface.
Height of a prism is the distance between the bases.

If the lateral faces are perpendicular to the bases, the prism is called right prism or rectangular box. Othes prisms are called oblique prisms.
The length of the lateral edges of a right prism equals the height of the prism and the lateral sides are rectangles.
If a right prism has regular polygons for the bases, then we say it is regular. Lateral faces of a regular right prism are congruent rectangles.

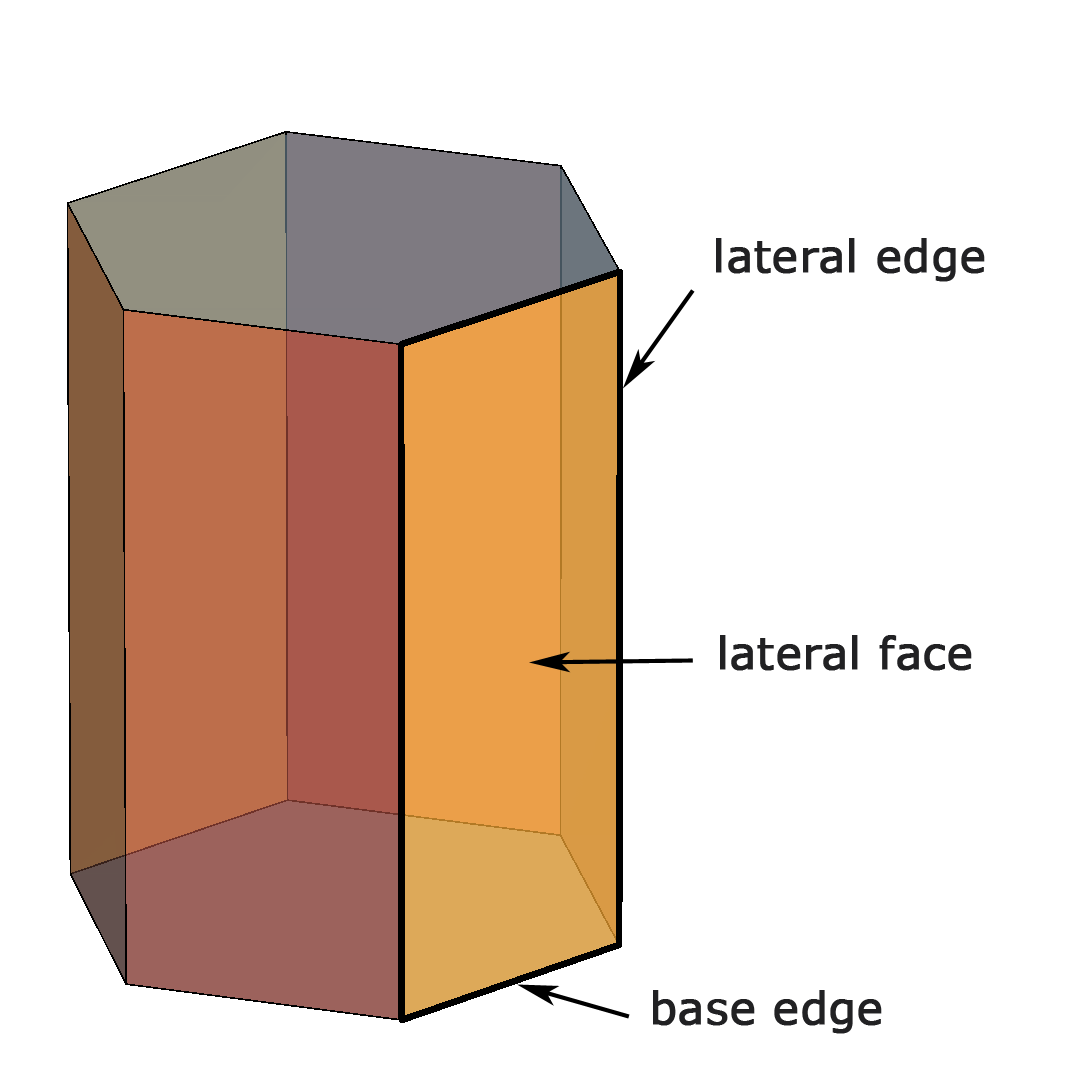
A regular hexagonal prism An oblique hexagonal prism


Pyramids

Let B be a convex polygon in the space and V a point in the space not in the plane of the polygon.
Polyhedron with the base B and whose lateral faces are triangles VBiBj (where Bi, Bj are two adjacent vertices of the polygon B) is called a pyramid.

Polygon B is called the base of the pyramid, point V apex (vertex), triangles VBiBj lateral sides, line segments VBi lateral edges and the set of all lateral sides VBiBj is called the lateral surface of the pyramid.
Height of the pyramid is the distance between the apex V and the plane of the base.

If the apex lies directly above the center of the base, the pyramid is called right pyramid (this definition is valid if the base has a center point, that is the case if the base is regular polygon, rectangle etc.). Lateral sides of a right pyramid are isosceles triangles with congruent sides.
Other pyramids are called oblique.

If the base of the pyramid is a regular polygon, then the pyramid is a regular pyramid.
Lateral sides of the regular pyramid are isosceles triangles.



A regular hexagonal pyramid An oblique hexagonal pyramid

Curved solids

Curves solids are solids whose boundary contains some curved surfaces.

Cylinders

By a cylinder we mean circular cylinder.
Circular cylinder is a solid bounded by two congruent circles K1(S1,r) and K2(S2,r) that lie in parallel planes and we call them the bases of the cylinder, and its side is a ruled surface that consists of lines T1T2, where (T1 ∈ K1, T2 ∈ K2) and T1T2 || S1S2 and is called lateral surface. The lines T1T2 are called the generatrices of the cylinder. All generatrices are congruent.

The line S1S2 is called the axis of the cylinder.
If the axis of the cylinder is perpendicular to the bases, we call this cylinder right cylinder and every circular right cylinder is cylinder of revolution . It is obtained by the rotation of a generatrix T1T2 around the axis S1S2. Lenght of the generatrix equals the height of the cylinder of revolution.
Other cylinders are called oblique.

Plane that contains the axis of the cylinder is called axial cross-section plane.
Such planes intersect the cylinder at a rectangle.
If the axial cross-section is a square, the length of a generatrix equals the diameter of the base circle, we call the cylinder equilateral.
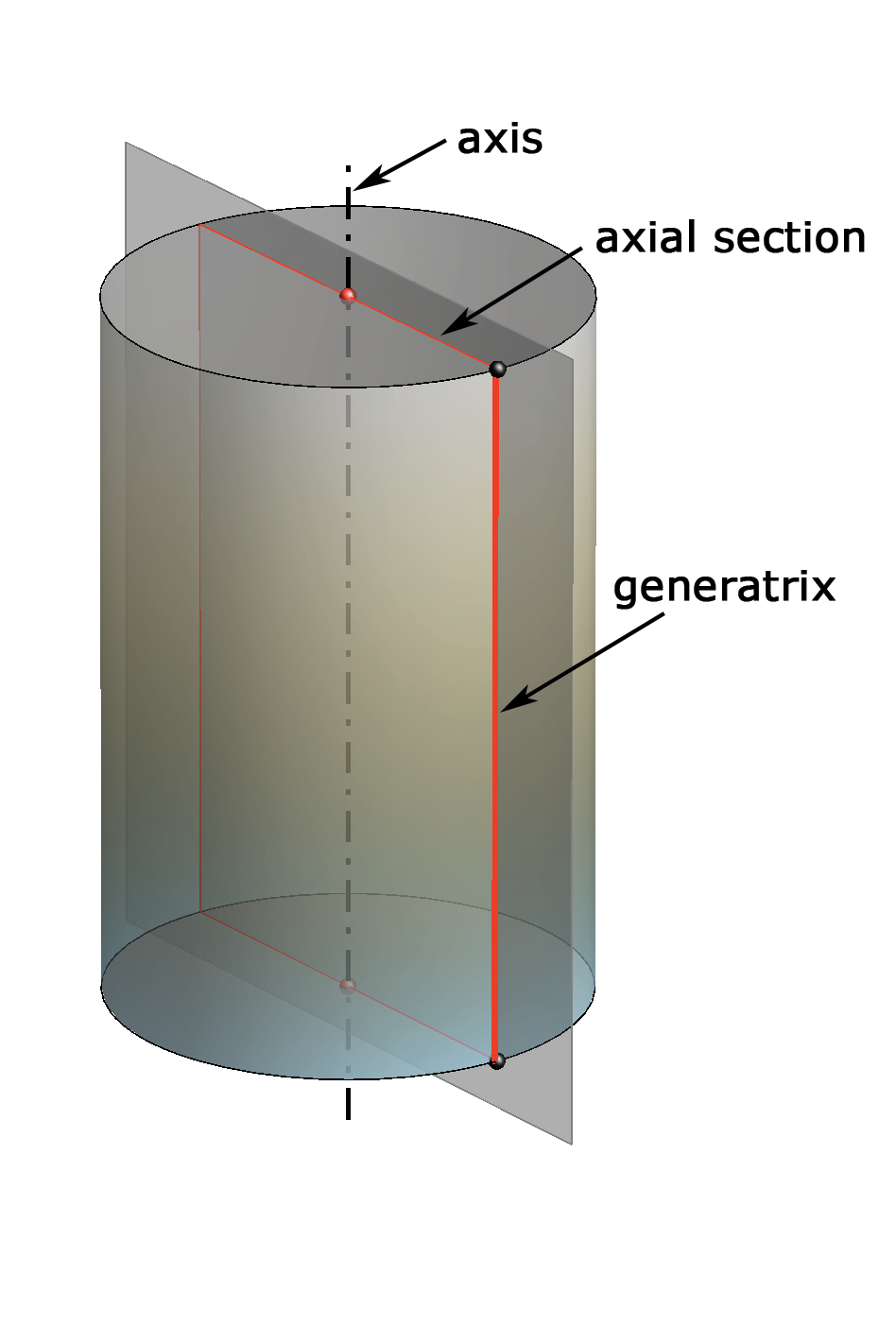
A right circular cylinder– cylinder of revolution An oblique circular cylinder


Cones

By a cone we mean circular cone.
Let K be a circle and V any point that does not lie in the plane of the circle K. A solid bounded by the circle K and the curved surface that consists of the lines VT, where T ∈ K, is called a cone.
The circle K is called the base of the cone, the curved surface is the lateral surface, and lines VT are called generatrices of the cone.

The line VS, where S is the center of the base of the cone, is called the axis of the cone.
If the axis is perpendicular to the base of the cone, we say the cone is a right cone. All other cones are called oblique.
Right circular cone is the cone of revolution, its lateral surface is obtained by the rotation of the generatrix VT around the axis VS.

A plane that contains the axis of the cone is called axial cross-section plane.
Axial cross-section of the cone is a icosceles triangle.
If the axial cross-section is an equilateral triangle, then the cone is called an equilateral cone and the length of a generatrix equals the diameter of the base.
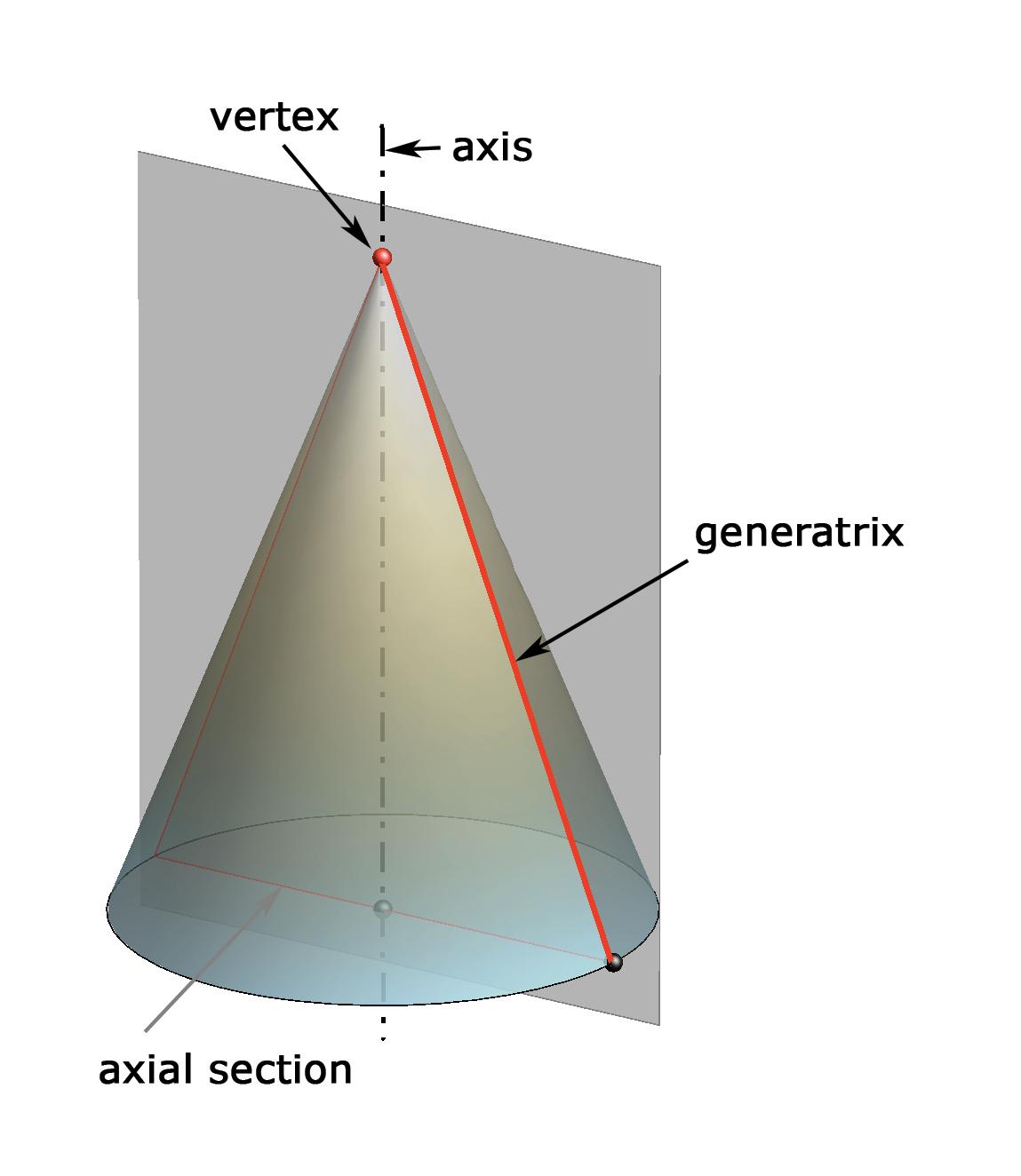
A right circular cone - cone of revolution An oblique circular cone


Balls

A ball is a set of points in the space whose distance to the fixed point S is less or equal to a positive constant r.
The point S is called the center of the ball, the number r is called the radius of the ball.

The boundary of the ball consists of one curved surface that is called the sphere.
The sphere is a set of points in space whose distance to the point S equals r.

Plane intersections of the sphere (plane curves lying on the sphere) are circles.
Circles on the sphere with the same center and radius as the sphere are called great circles.

Intersections of horizontal planes and the sphere are called the lines of latitude, the longest among them is called the equator.

Great circles that contain the endpoints of the vertical diameter of the sphere (the poles) are called the lines of longitude or meridians.


the sphere the lines of latitude the meridians



Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb