Orthogonal Projection of a Straight Line
If a straight line p is not a ray of projection (not perpendicular to
either projection plane), then its horizontal and vertical projections are
lines p' and p''.
Hence, in Monge's projection, a straight line is represented by a pair of
projections (p',p'').
A point T lies on a line p if its horizontal projection lies on the
horizontal projection of the line and its vertical projection lies on the
vertical projection of the line.
The reverse also holds, so we can state: T ∈ p <=> T' ∈ p' & T'' ∈ p''.
A point P1 where the line p
intersects the horizontal plane is called horizontal
trace of the line p, P1 = p ∩ Π1.
A point P2 where the line p pierces
the vertical plane is called the vertical trace of the
line p, P2 = p ∩ Π2.

CONSTRUCTION of TRACES
Angles of inclination of a straight line to the planes of projection
First angle of inclination ω1
of a line p is the angle between the line and the horizontal plane Π1.
It is also called slope angle.
It equals the angle between the line and its horizontal projection. ω1 = ∠(p,p').
Second angle of inclination ω2
of a line p is the angle between the line and the vertical plane Π2,
i.e. ω2 = ∠(p,p'').
Construction of these angles will be explained later.
|

|
Straight lines in special positions
A line parallel to the horizontal plane
Π1 is called horizontal
(level) line and all its points have the same distance to the
horizontal plane, i.e. have the same z-coordinate.
Therefore, the vertical projection of that
line is parallel to the ground line x. The reverse also holds,
so we can state: p || Π1 <=> p'' ||
x.
A horizontal line does not have a horizontal trace.

If the vertical projection of a
line is parallel to the x-axis, then the line is parallel to the
horizontal plane.
If a line is parallel to the vertical plane Π2 all its points have the same distance to the vertical plane, i.e. have the same y-coordinate.
Such line is called vertical (frontal) line. Hence, the
horizontal projection of the line is parallel to the x-axis. The reverse also holds,
so we state: p || Π2 <=> p' || x.
A vertical line does not have a vertical traces.

If the horizontal projection of a
line is parallel to the x-axis, then the line is parallel to the vertical
plane.
If a line is contained in the plane Π1 ( Π2), then
the vertical (horizontal)
projection of the line coincide with x-axis.
The reverse holds.
If a line is parallel to the x-axis, then its
horizontal and vertical projections are also parallel to x. The reverse holds.

If the horizontal and vertical
projections of a line are parallel to the x-axis, then the line is
parallel to x.
If a line is perpendicular to the plane Π1 , then
its horizontal projection is a point and
its vertical projection is perpendicular
to the x-axis.
If a line is perpendicular to the plane Π2 , then
its vertical projection is a point and
its horizontal projection is perpendicular
to x-axis.

A line perpendicular to either
projection plane is a ray of projection and projects to a point.
Relative positions of lines
If the lines a and b are parallel, then they have
parallel horizontal projections and
parallel vertical projections. The reverse also holds, so we
can state: a || b <=> a' || b' & a'' || b''.
If the lines a and b are intersecting lines, then the intersection
of their horizontal projections and the intersection of their vertical projections lie on the
same line of recall.
The reverse holds.
If the lines a and b are skew lines, then the intersections of their horizontal and vertical projections do not lie on the same
line of recall. The reverse holds.

|

|

|
|
Parallel lines |
Intersecting lines |
Skew lines |
Straight line, symmetry plane, coincidence plane
Due to the property of the points lying in the symmetry plane or the
coincidence plane, it is very easy to construct the intersection of a line p with these
planes.
The construction is shown on the figure below.
If a line is contained in the symmetry plane, then its
horizontal and vertical projections are symmetrical with respect to the
x-axis.
If a line is parallel to the symmetry plane, then its projections
have the same angle to the x-axis.
If a line is contained in the coincidence plane, then its horizontal
and vertical projections coincide.
If a line is parallel to the coincidence plane, then its projections are
parallel.

S = p ∩ Σ, K = p ∩ Κ
|
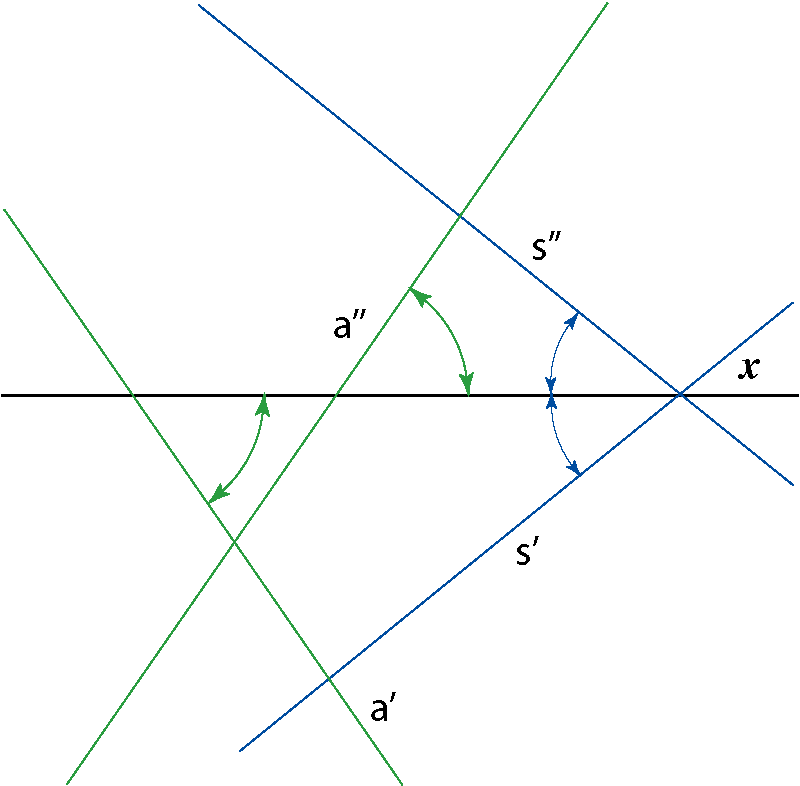
s ⊂ Σ, a || Σ
|

k ⊂ Κ, b || Κ
|
Created by Sonja Gorjanc 3DGeomTeh - Developing project of the University of Zagreb.
Translated by Helena Halas and Iva Kodrnja.












