Projiciranje pravca

Ukoliko pravac p nije zraka projiciranja (u Mongeovom projiciranju zrake su okomite na ravnine projekcije) njegov tlocrt i nacrt su pravci p' i p''.
Dakle, u Mongeovoj projekciji pravac prikazujemo parom njegovih projekcija (p',p'').

Točka T leži na pravcu p ako njen tlocrt leži na tlocrtu, a nacrt na nacrtu pravca p.
Budući da vrijedi i obrat, možemo pisati: T ∈ p <=> T' ∈ p' & T'' ∈ p''.

Točku P1 u kojoj pravac p probada 1. ravninu projekcije nazivamo prvim probodištem pravca p, P1 = p ∩ Π1.
Točku P2 u kojoj pravac p probada 2. ravninu projekcije nazivamo drugim probodištem pravca p, P2 = p ∩ Π2.


KONSTRUKCIJA

Prvi i drugi prikloni kut pravca

  • Prvi prikloni kut ω1 nekog pravca p je kut što ga on zatvara s ravninom tlocrta Π1.
    Prema definiciji kuta između pravca i ravnine, to je kut između pravca p i njegovog tlocrta, tj. ω1 = ∠(p,p').

  • Drugi prikloni kut ω2 nekog pravca p je kut što ga on s zatvara ravninom nacrta Π2, tj. ω2 = ∠(p,p'').


    Konstrukciju ovih kuteva u Mongeovom projiciranju objasnit ćemo kasnije.


    • Posebni položaji pravca

  • Ako je pravac paralelan s ravninom Π1 , tada su sve njegove točke jednako udaljene od te ravnine, tj. imaju istu z-koordinatu.
    Stoga je nacrt tog pravca paralelan s osi x. Budući da vrijedi i obrat, možemo pisati: p || Π1 <=> p'' || x.
    Takav pravac ima u konačnosti samo drugo probodište.

    Ako je nacrt pravca paralelan s osi x, onda je pravac paralelan s ravninom Π1.


  • Ako je pravac paralelan s ravninom Π2, tada su sve njegove točke jednako udaljene od te ravnine, tj. imaju istu y-koordinatu.
    Stoga je tlocrt tog pravca paralelan s osi x. Vrijedi i obrat, pa pišemo: p || Π2 <=> p' || x.
    Takav pravac ima u konačnosti samo prvo probodište.

    Ako je tlocrt pravca paralelan s osi x, onda je pravac paralelan s ravninom Π2.


  • Ako pravac leži u ravnini Π1 ( Π2), tada se nacrt (tlocrt) tog pravca podudara s osi x. Vrijedi obrat.

  • Ako je pravac paralelan s osi x, onda su mu i tlocrt i nacrt paralelni s x. Vrijedi obrat.

    Ako je su tlocrt i nacrt pravca paralelani s osi x, onda je pravac paralelan s osi x.


  • Ako je pravac okomit na ravninu Π1 , tada je njegov tlocrt jedna točka, a nacrt mu je okomit na os x.

  • Ako je pravac okomit na ravninu Π2, tada je njegov nacrt jedna točka, a tlocrt mu je okomit na os x.

    Pravci okomiti na ravnine projekcije su zrake projiciranja i uvijek im je jedna projekcija točka.

    Dva pravca

  • Ako su pravci a i b paralelni, onda su paralelne i njihove odgovarajuće projekcije.
    Vrijedi i obrat pa pišemo: a || b <=> a' || b' & a'' || b''.

  • Ako se pravci a i b sijeku, tada sjecište njihovih tlocrta i sjecište njihovih nacrta leže na istoj ordinali. Vrijedi obrat. \(^*\)

  • Ako su pravci a i b mimosmjerni, tada sjecište njihovih tlocrta i sjecište njihovih nacrta ne leže na istoj ordinali. Vrijedi obrat. \(^*\)

    Pravci a i b su paralelni. Pravci a i b su ukršteni. Pravci a i b su mimosmjerni.


    \(^*\) Ove se tvrdnje ne odnose na slučajeve kada se projekcije pravca podudaraju s ordinalom, odnosno kada je pravac okomit na os x.

    Pravac i ravnine simetrije i koincidencije

    Na temelju svojstava što ih imaju projekcije točaka koje leže u ravninama simetrije i koincidencije, za zadani je pravac p (p',p'') vrlo jednostavno konstruirati projekcije njegovih probodišta s tim ravninama.
    Ta je jednostavna konstrukcija dana na donjoj lijevoj slici.

  • Ako pravac leži u ravnini simetrije tada su njegov tlocrt i nacrt simetrični s obzirom na os x.
  • Ako je pravac paralelan s ravninom simetrije tada njegov tlocrt i nacrt zatvaraju jednake kuteve (suprotno orijentirane) s osi x.

  • Ako pravac leži u ravnini koincidencije tada se njegov tlocrt i nacrt podudaraju.
  • Ako je pravac paralelan s ravninom koincidencije tada su njegov tlocrt i nacrt paralelni.





    S = p ∩ Σ, K = p ∩ Κ

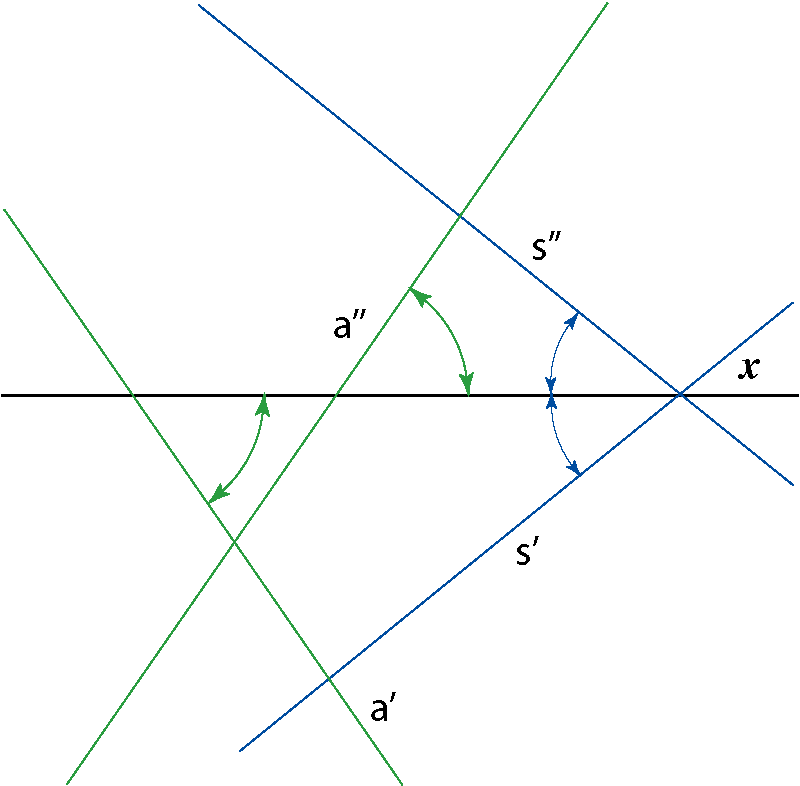    s ⊂ Σ, a || Σ


    k ⊂ Κ, b || Κ



    Sonja Gorjanc - 3DGeomTeh - Razvojni projekt Sveučilišta u Zagrebu