Zadatak: Konstruirajte projekcije probodišta pravca \( p\) i zadanog stošca.
Princip konstrukcije probodišta pravca i neke plohe je sljedeći: Pravcem postavimo proizvoljnu ravninu, konstruiramo presječnu krivulju te ravnine i plohe, a točke u kojima se sijeku pravac i dobivena presječna krivulja su tražena probodišta. Ravninu postavljamo tako da nam konstrukcija presječne krivulje bude što jednostavnija, a u slučaju rotacijskog stošca to su:
- ravnine koje prolaze vrhom (sijeku stožac u dvije izvodnice), ili
- ravnine koje su okomite na os stošca (sijeku stožac po kružnicama)



Prezentacija 65
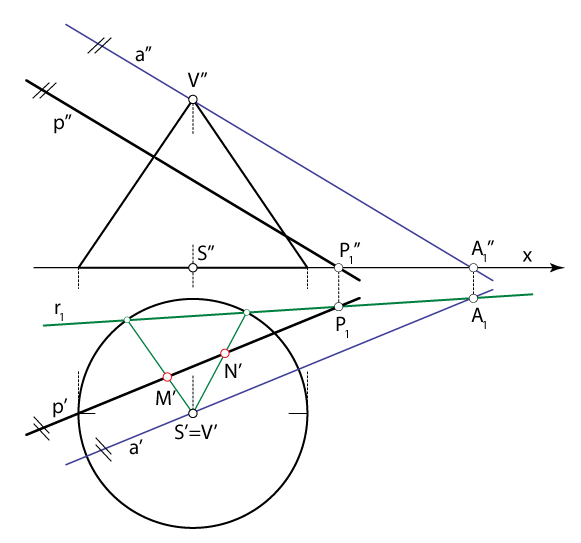
- Pravac \(\small p\) nije okomit na os zadanog stošca pa njime ne možemo postaviti ravninu koja taj stožac siječe po kružnici
- Konstruiramo prvi trag ravnine \(\small\mathrm P\) koja sadrži pravac \(\small p\) i vrh \(\small V\) (pomoću pravca \(a\) koji je paralelan s \(\small p\), a prolazi točkom \(\small V\))
- Konstruiramo tlocrte izvodnica po kojima ravnina \(\small\mathrm P\) siječe zadani stožac
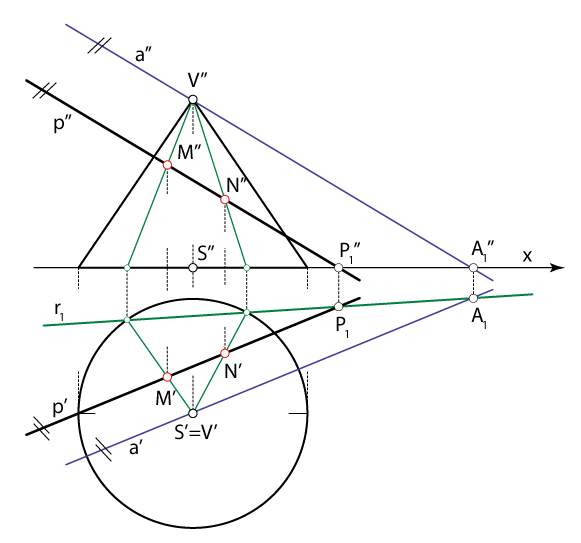
- Konstruiramo projekcije točaka \(\small M\) i \(\small N\) u kojima dobivene izvodnice sijeku pravac \(\small p\). To su projekcije probodišta pravca \(\small p\) i zadanog stošca
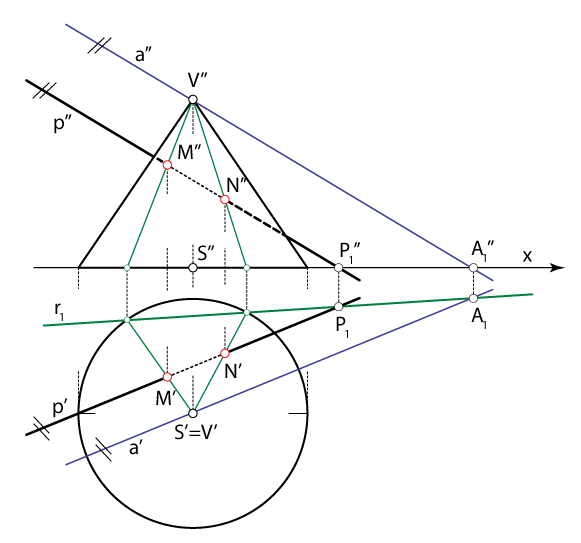
- Na završnom crtežu pravc \(\small p\) iscrtavamo na sljedeći način:
- dio u prodoru (unutar stošca) - točkano,
- dio izvan prodora koji je u projekciji zaklonjen plohom - crtkano,
- ostale dijelove pravca crtamo punom linijom


Prezentacija 66
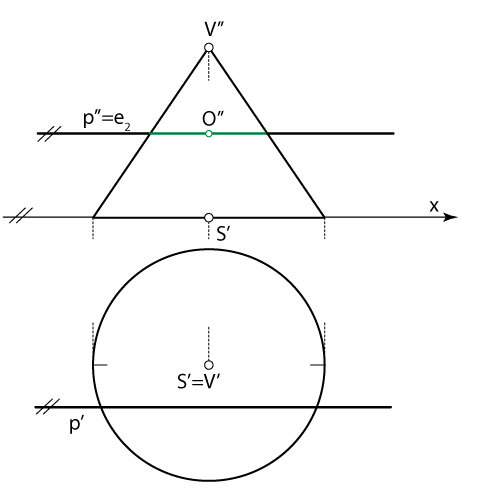
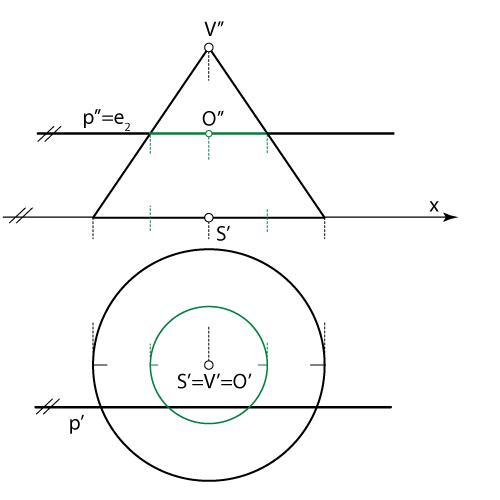
- U ovom je slučaju pravac \(\small p\) okomit na os stošca pa njime možemo postaviti ravninu \( \small\mathrm E\) koja taj stožac siječe po kružnici. Nacrt presječne kružnice je dužina, jer je ravnina \( \small\mathrm E\) 2. projicirajuća
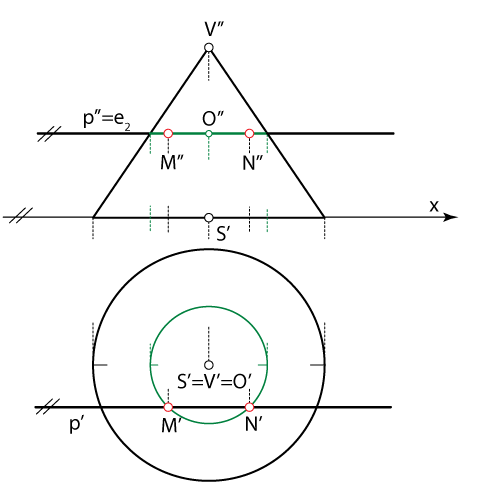
- Konstruiramo tlocrt presječne kružnice
- Konstruiramo projekcije točaka \(\small M\) i \(\small N\) u kojima presječna kružnica siječe pravac \(\small p\). Te su točke projekcije probodišta pravca \(\small p\) i zadanog stošca
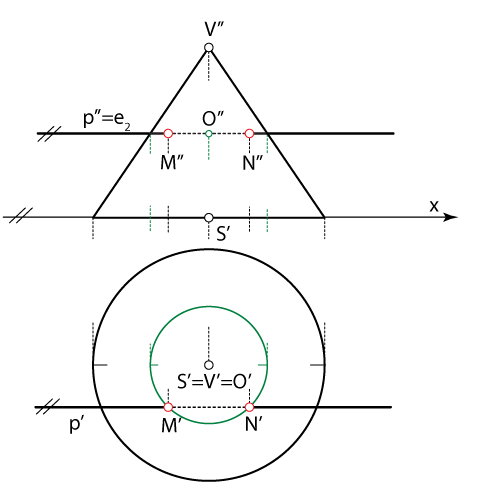
- Na završnom crtežu dio pravca \(\small p\) koji se nalazi unutar stošca iscrtavamo točkanom linijom